Band 5 – Page 33

Mechanics, EXT2 M1 2023 HSC 13c

A particle of mass 1 kg is projected from the origin with speed 40 m s$ ^{-1}$ at an angle 30° to the horizontal plane.

Use the information above to show that the initial velocity of the particle is
$\mathbf{v}(0)={\displaystyle\left(\begin{array}{cc}20 \sqrt{3} \\ 20\end{array}\right)} $. (1 mark)

--- 6 WORK AREA LINES (style=lined) ---

The forces acting on the particle are gravity and air resistance. The air resistance is proportional to the velocity vector with a constant of proportionality 4 . Let the acceleration due to gravity be 10 m s $ ^{-2}$.

The position vector of the particle, at time $t$ seconds after the particle is projected, is $\mathbf{r}(t)$ and the velocity vector is $\mathbf{v}(t)$.

Show that $\mathbf{v}(t)={\displaystyle \left(\begin{array}{cc}20 \sqrt{3} e^{-4 t} \\ \dfrac{45}{2} e^{-4 t}-\dfrac{5}{2}\end{array}\right)}$ (3 marks)

--- 12 WORK AREA LINES (style=lined) ---
Show that $\mathbf{r}(t)=\left(\begin{array}{c}5 \sqrt{3}\left(1-e^{-4 t}\right) \\ \dfrac{45}{8}\left(1-e^{-4 t}\right)-\dfrac{5}{2} t\end{array}\right)$ (2 marks)

--- 10 WORK AREA LINES (style=lined) ---
The graphs $y=1-e^{-4 x}$ and $y=\dfrac{4 x}{9}$ are given in the diagram below.
Using the diagram, find the horizontal range of the particle, giving your answer rounded to one decimal place. (2 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{Proof (See Worked Solutions)}$
$\text{Proof (See Worked Solutions)}$
$\text{Proof (See Worked Solutions)}$
$8.7\ \text{metres}$

Show Worked Solution

$\underset{\sim}{v}(0)={\displaystyle\left(\begin{array}{cc} 40 \cos\ 30° \\ 40 \sin\ 30°\end{array}\right)} = {\displaystyle\left(\begin{array}{cc} 40 \times \frac{\sqrt3}{2} \\ 40 \times \frac{1}{2}\end{array}\right)} = {\displaystyle\left(\begin{array}{cc}20 \sqrt{3} \\ 20\end{array}\right)} $

ii. $\text{Air resistance:} $

$\underset{\sim}{F} = -4\underset{\sim}{v} = {\displaystyle\left(\begin{array}{cc} -4\dot{x} \\ -4\dot{y} \end{array}\right)} $

$\text{Horizontally:}$

$1 \times \ddot{x} $	$=-4 \dot{x} $
$\dfrac{d\dot{x}}{dt}$	$=-4\dot{x}$
$\dfrac{dt}{d\dot{x}}$	$= -\dfrac{1}{4\dot{x}} $
$t$	$=-\dfrac{1}{4} \displaystyle \int \dfrac{1}{\dot{x}} \ d\dot{x} $
$-4t$	$=\ln \|\dot{x}\|+c $

$\text{When}\ \ t=0, \ \dot{x}=20\sqrt3 \ \ \Rightarrow\ \ c=-\ln{20\sqrt3} $

$-4t$	$=\ln\|\dot{x}\|-\ln 20\sqrt3 $
$-4t$	$=\ln\Bigg{\|}\dfrac{\dot{x}}{20\sqrt{3}} \Bigg{\|} $
$\dfrac{\dot{x}}{20\sqrt{3}} $	$=e^{-4t} $
$\dot{x}$	$=20\sqrt{3}e^{-4t}$

$\text{Vertically:} $

$1 \times \ddot{y} $	$=-1 \times 10-4 \dot{y} $
$\dfrac{d\dot{y}}{dt}$	$=-(10+4\dot{y})$
$\dfrac{dt}{d\dot{y}}$	$= -\dfrac{1}{10+4\dot{y}} $
$t$	$=- \displaystyle \int \dfrac{1}{10+4\dot{y}} \ d\dot{y} $
$-4t$	$=- \displaystyle \int \dfrac{4}{10+4\dot{y}} \ d\dot{y} $
$-4t$	$=\ln \|10+4\dot{y}\|+c $

$\text{When}\ \ t=0, \ \dot{y}=20 \ \ \Rightarrow\ \ c=-\ln{90} $

$-4t$	$=\ln\|10+4\dot{y}\|-\ln 90 $
$-4t$	$=\ln\Bigg{\|}\dfrac{10+4\dot{y}}{\ln{90}} \Bigg{\|} $
$\dfrac{10+4\dot{y}}{90} $	$=e^{-4t} $
$4\dot{y}$	$=90e^{-4t}-10$
$\dot{y}$	$=\dfrac{45}{2} e^{-4t}-\dfrac{5}{2} $

$\therefore \underset{\sim}v={\displaystyle \left(\begin{array}{cc}20 \sqrt{3} e^{-4 t} \\ \dfrac{45}{2} e^{-4 t}-\dfrac{5}{2}\end{array}\right)}$

iii. $\text{Horizontally:}$

$x$	$= \displaystyle \int \dot{x}\ dx$
	$= \displaystyle \int 20\sqrt3 e^{-4t}\ dt $
	$=-5\sqrt3 e^{-4t}+c $

$\text{When}\ \ t=0, \ x=0\ \ \Rightarrow\ \ c=5\sqrt3 $

$x$	$=5\sqrt3-5\sqrt3 e^{-4t} $
	$=5\sqrt3(1-e^{-4t}) $

$\text{Vertically:}$

$y$	$= \displaystyle \int \dot{y}\ dx$
	$= \displaystyle \int \dfrac{45}{2} e^{-4t}-\dfrac{5}{2}\ dt $
	$=-\dfrac{45}{8}e^{-4t}-\dfrac{5}{2}t+c $

$\text{When}\ \ t=0, \ y=0\ \ \Rightarrow\ \ c= \dfrac{45}{8} $

$y$	$=\dfrac{45}{8}-\dfrac{45}{8} e^{-4t}-\dfrac{5}{2}t $
	$=\dfrac{45}{8}(1-e^{-4t})-\dfrac{5}{2} $

$\therefore \underset{\sim}{r}=\left(\begin{array}{c}5 \sqrt{3}\left(1-e^{-4 t}\right) \\ \dfrac{45}{8}\left(1-e^{-4 t}\right)-\dfrac{5}{2} t\end{array}\right)$

iv. $\text{Range}\ \Rightarrow\ \text{Find}\ \ t\ \ \text{when}\ \ y=0: $

$\dfrac{45}{8}(1-e^{-4t})-\dfrac{5}{2}t $	$=0$
$\dfrac{45}{8}(1-e^{-4t}) $	$=\dfrac{5}{2}t $
$1-e^{-4t}$	$=\dfrac{4}{9}t $

$\text{Graph shows intersection of these two graphs.}$

$\Rightarrow \text{Solution when}\ \ t\approx 2.25$

$\therefore\ \text{Range}$	$=5\sqrt3(1-e^{(-4 \times 2.25)}) $
	$=8.659…$
	$=8.7\ \text{metres (to 1 d.p.)}$

♦ Mean mark (iv) 43%.

Mechanics, EXT2 M1 2023 HSC 12c

An object with mass $m$ kilograms slides down a smooth inclined plane with velocity $ \underset{\sim}{v}(t)$, where $t$ is the time in seconds after the object started sliding down the plane. The inclined plane makes an angle $\theta$ with the horizontal, as shown in the diagram. The normal reaction force is $\underset{\sim}{R}$. The acceleration due to gravity is $\underset{\sim}{g}$ and has magnitude $g$. No other forces act on the object.

The vectors $\underset{\sim}{i}$ and $ \underset{\sim}{j} $ are unit vectors parallel and perpendicular, respectively, to the plane, as shown in the diagram.

Show that the resultant force on the object is $\underset{\sim}{F}=-(m g \ \sin \theta) \underset{\sim}{i}$. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Given that the object is initially at rest, find its velocity $\underset{\sim}{v}(t)$ in terms of $g$, $\theta, t$ and $\underset{\sim}{i}$. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

i. $\text{Proof (See Worked Solution)} $

ii. $\underset{\sim}{v}=-gt\ \sin \theta \ \underset{\sim}{i} $

Show Worked Solution

$\text{Resolving forces in}\ \underset{\sim}{j} \ \text{direction:} $

$ {\underset{\sim}{F}}_\underset{\sim}{j} = \underset{\sim}{R} + m\underset{\sim}{g}\ \cos \theta = 0\ \ \text{(in equilibrium)} $

$\text{Resolving forces in}\ \underset{\sim}{i} \ \text{direction:} $

$ {\underset{\sim}{F}}_\underset{\sim}{i} = -m\underset{\sim}{g} \ \sin \theta \ \ \ \text{(down slope)} $

$\therefore \text{Resultant force:}\ \ \underset{\sim}{F}=-(m g \ \sin \theta) \underset{\sim}{i} $

♦ Mean mark (i) 50%.

ii. $\text{Using}\ \ \underset{\sim}{F}=m \underset{\sim}{a}: $

$m \underset{\sim}{a}$	$=-mg\ \sin \theta \ \underset{\sim}{i} $
$\underset{\sim}{a}$	$=-g\ \sin \theta \ \underset{\sim}{i} $
$\underset{\sim}{v}$	$= \displaystyle \int \underset{\sim}{a}\ dt $
	$=-gt\ \sin \theta +c $

$\text{When}\ \ t=0,\ \ \underset{\sim}{v}=0\ \ \Rightarrow \ \ c=0 $

$\therefore \underset{\sim}{v}=-gt\ \sin \theta \ \underset{\sim}{i} $

PHYSICS, M6 2023 HSC 10 MC

Figure $\text{I}$ shows a current flowing through a loop of wire that is in a uniform magnetic field.

The loop is then rotated to the position shown in Figure $\text{II}$.

The magnitude of the force on the side $X Y$ and the magnitude of the torque on the loop in Figure $\text{II}$ are compared to those in Figure $\text{I}$.

Which row of the table correctly describes the comparison?

\begin{align*}
\begin{array}{l}
\rule{0pt}{2.5ex} \ \rule[-1ex]{0pt}{0pt}& \\
\rule{0pt}{2.5ex}\textbf{A.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{B.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{C.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{D.}\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|c|c|}
\hline
\rule{0pt}{2.5ex}\quad \textit{Force}\quad \rule[-1ex]{0pt}{0pt}&\quad \textit{Torque}\quad \\
\hline
\rule{0pt}{2.5ex}\text{I > II}\rule[-1ex]{0pt}{0pt}&\text{I = II}\\
\hline
\rule{0pt}{2.5ex}\text{I > II}\rule[-1ex]{0pt}{0pt}& \text{I > II}\\
\hline
\rule{0pt}{2.5ex}\text{I = II}\rule[-1ex]{0pt}{0pt}& \text{I = II} \\
\hline
\rule{0pt}{2.5ex}\text{I = II}\rule[-1ex]{0pt}{0pt}& \text{I > II} \\
\hline
\end{array}
\end{align*}

Show Answers Only

$D$

Show Worked Solution

The magnitude of the force on side $XY$ can be calculated by $ F= lIB \sin \theta$
As side $ XY$ is always perpendicular to the magnetic field, $ \theta = 90^{\circ} $ and Force $\text{I}$ = Force $\text{II}$
The magnitude of the torque on side $XY$ can be calculated by $ \tau=rF\sin\theta$
In Figure $\text{I}$, $ \theta= 90^{\circ} $ and in Figure $\text{II}$, $ \theta = 0^{\circ} $ → Torque $\text{I}$ > Torque $\text{II}$

$\Rightarrow D$

♦ Mean mark 52%.

Financial Maths, STD1 F3 2023 HSC 30

A plumber leases equipment which is valued at $60 000.

The salvage value of the equipment at any time can be calculated using either of the two methods of depreciation shown in the table.

\begin{array} {|l|c|}
\hline
\rule{0pt}{2.5ex} \textit{Method of depreciation} \rule[-1ex]{0pt}{0pt} & \textit{Rate of depreciation} \\
\hline
\rule{0pt}{2.5ex} \text{Straight-line method} \rule[-1ex]{0pt}{0pt} & \text{\$3500 per annum} \\
\hline
\rule{0pt}{2.5ex} \text{Declining-balance method} \rule[-1ex]{0pt}{0pt} & \text{12% per annum} \\
\hline
\end{array}

Under which method of depreciation would the salvage value of the equipment be lower at the end of 3 years? Justify your answer with appropriate mathematical calculations. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{Straight-line method:}$

$S$	$=V_0-Dn$
	$=60\ 000-3500\times 3$
	$=$49\ 500$

$\text{Declining-balance method:}$

$S$	$=V_0(1-r)^n$
	$=60\ 000(1-0.12)^3$
	$=60\ 000(0.88)^3$
	$=$40\ 888.32$

$\text{Salvage value is lower for the declining-balance method.}$

Show Worked Solution

$\text{Straight-line method:}$

$S$	$=V_0-Dn$
	$=60\ 000-3500\times 3$
	$=$49\ 500$

$\text{Declining-balance method:}$

$S$	$=V_0(1-r)^n$
	$=60\ 000(1-0.12)^3$
	$=60\ 000(0.88)^3$
	$=$40\ 888.32$

$\text{Salvage value is lower for the}$

$\text{declining-balance method.}$

♦ Mean mark 48%.

Measurement, STD1 M4 2023 HSC 28

The nutrition label for a food item is shown.

Based on the information on this label, what is the daily recommended intake of carbohydrates, to the nearest gram? (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

$318\ \text{g}$

Show Worked Solution

$6\text{% of daily intake}$	$=19.1\ \text{g}$
$\text{daily intake}$	$=\dfrac{19.1}{6}\times 100$
	$=318.\dot{3}\ \text{g}$
	$\approx 318\ \text{g/day}$

♦ Mean mark 42%.

Measurement, STD1 M3 2023 HSC 29

The diagram shows the location of three places $X$, $Y$ and $C$.

$Y$ is on a bearing of 120° and 15 km from $X$.

$C$ is 40 km from $X$ and lies due west of $Y$.

$P$ lies on the line joining $C$ and $Y$ and is due south of $X$.

Find the distance from $X$ to $P$. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
What is the bearing of $C$ from $X$, to the nearest degree? (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

$7.5\ \text{km}$
$259^{\circ}$

Show Worked Solution

a. $\text{In}\ \Delta XPY:$

$\angle PXY=180-120=60^{\circ}$

$\cos 60^{\circ}$	$=\dfrac{XP}{15}$
$XP$	$=15\times \cos 60^{\circ}$
	$=7.5\ \text{km}$

♦♦ Mean mark (a) 24%.

b. $\text{In}\ \Delta XPC:$

$\text{Let}\ \theta = \angle CXP$

$\cos \theta$	$=\dfrac{7.5}{40}$
$\theta$	$=\cos^{-1} \Big(\dfrac{7.5}{40}\Big)$
	$=79.193…$
	$=79^{\circ}\ \text{(nearest degree)}$

$\text{Bearing}\ C\ \text{from}\ X$	$=180+79$
	$=259^{\circ}$

♦♦♦♦ Mean mark (b) 9%.

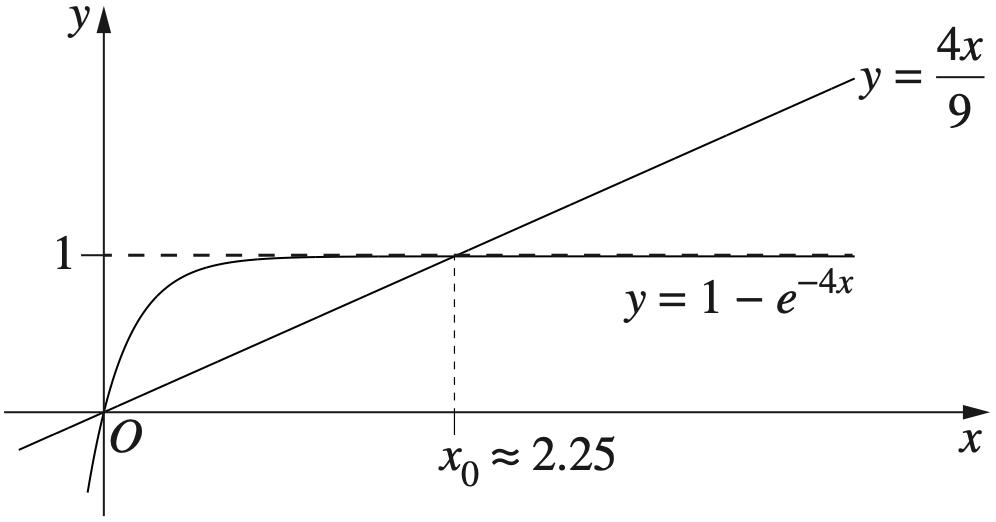
Calculus, EXT1 C2 2023 HSC 14a

Let $f(x)=2 x+\ln x$, for $x>0$.

Explain why the inverse of $f(x)$ is a function. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---
Let $g(x)=f^{-1}(x)$. By considering the value of $f(1)$, or otherwise, evaluate $g^{\prime}(2)$. (2 mark)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

i. $f(x)=2 x+\ln x$

$f^{′}(x)=2+\dfrac{1}{x} $

$\text{In domain}\ x \gt 0\ \ \Rightarrow f^{-1}(x) \gt 0 \ \ (f(x)\ \text{is monotonically increasing}) $

$\text{Since}\ f(x)\ \text{is one-to-one,}\ f^{-1}(x)\ \text{is a function.} $

ii. $\dfrac{1}{3}$

Show Worked Solution

i. $f(x)=2 x+\ln x$

$f^{′}(x)=2+\dfrac{1}{x} $

$\text{In domain}\ x \gt 0\ \ \Rightarrow f^{-1}(x) \gt 0 \ \ (f(x)\ \text{is monotonically increasing}) $

$\text{Since}\ f(x)\ \text{is one-to-one,}\ f^{-1}(x)\ \text{is a function.} $

Mean mark (i) 54%.

ii. $g(x)=f^{-1}(x) $

$f(g(x))=x$

$\text{Differentiate both sides:}$

$g^{′}(x)\ f^{′}(g(x))$	$=1$
$g^{′}(x)$	$=\dfrac{1}{f^{′}(g(x))}$
$g^{′}(2)$	$=\dfrac{1}{f^{′}(g(2))}$

$f(1)=2 \times 1 + \ln1 = 2 $

$\Rightarrow g(2)=1 \ \text{(by inverse definition)}$

$\therefore g^{′}(2)$	$= \dfrac{1}{f^{′}(1)} $
	$=\dfrac{1}{2+\frac{1}{1}}$
	$=\dfrac{1}{3} $

♦♦ Mean mark (ii) 32%.

Vectors, EXT1 V1 2023 HSC 13b

Particle $A$ is projected from the origin with initial speed $v$ m s$^{-1}$ at an angle $\theta$ with the horizontal plane. At the same time, particle $B$ is projected horizontally with initial speed $u$ ms$^{-1}$ from a point that is $H$ metres above the origin, as shown in the diagram.

The position vector of particle $A, t$ seconds after it is projected, is given by

\[\textbf{r}_A(t)=\left(\begin{array}{c}v t\ \cos \theta \\vt\ \sin\theta-\dfrac{1}{2} g t^2\end{array}\right) \text{. (Do NOT prove this.)}\]

The position vector of particle $B, t$ seconds after it is projected, is given by

\[\textbf{r}_B(t)=\left(\begin{array}{c}u t \\H-\dfrac{1}{2} g t^2\end{array}\right) \text{. (Do NOT prove this.)}\]

The angle $\theta$ is chosen so that $\tan \theta=2$.

The two particles collide.

By first showing that $\cos \theta=\dfrac{1}{\sqrt{5}}$, verify that $v=\sqrt{5} u$. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Show that the particles collide at time $T=\dfrac{H}{2 u}$. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---

When the particles collide, their velocity vectors are perpendicular.

Show that $H=\dfrac{2 u^2}{g}$. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Prior to the collision, the trajectory of particle $A$ was a parabola. (Do NOT prove this.)
Find the height of the vertex of that parabola above the horizontal plane. Give your answer in terms of $H$. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{See Worked Solutions}$
$\text{See Worked Solutions}$
$\text{See Worked Solutions}$
$H$

Show Worked Solution

i. $\text{Given}\ \ \tan \theta =2$

$\cos \theta = \dfrac{1}{\sqrt 5} $

$\text{Since particles collide, for some}\ t: $

$vt\ \cos \theta$	$=ut$
$v \cdot \dfrac{1}{\sqrt 5} $	$=u$
$v$	$=\sqrt5 u$

ii. $\text{Equating y-components of}\ \textbf{r}_A\ \text{and}\ \textbf{r}_B : $

$vt\ \sin \theta-\dfrac{1}{2}gt^2$	$=H-\dfrac{1}{2}gt^2$
$vt\ \sin \theta$	$=H$
$u \sqrt{5} \times t \times \dfrac{2}{\sqrt5} $	$=H$
$t$	$= \dfrac{H}{2u} $

iii. $\text{Velocity vectors:} $

\[\textbf{v}_A(t)=\left(\begin{array}{c}v\ \cos \theta \\v\ \sin\theta-gt\end{array}\right)=\left(\begin{array}{c} u \\ 2u-gt \end{array}\right)\]

\[\textbf{v}_B(t)=\left(\begin{array}{c}u \\-gt \end{array}\right)\]

$\text{Since particles are perpendicular at collision:}$

$\textbf{v}_A \cdot \textbf{v}_B=0$

♦♦ Mean mark (iii) 37%.

$u^2+(-gt)(2u-gt)$	$=0$
$u^2-2gtu+g^2t^2$	$=0$
$(u-gt)^2$	$=0$
$gt$	$=u$
$t$	$=\dfrac{u}{g}$
$\dfrac{H}{2u}$	$=\dfrac{u}{g}\ \ \text{(see part (ii))}$
$\therefore H$	$=\dfrac{2u^2}{g}$

iv. $\text{Height of vertex}\ \ \Rightarrow \ \text{Find}\ t\ \text{when y-component of}\ \textbf{v}_A=0 $

$v\ \sin \theta-gt$	$=0$
$t$	$=\dfrac{v\ \sin \theta}{g} $

$\text{Height of vertex}\ =\ \text{y-component of}\ \textbf{r}_A\ \text{when}\ \ t= \dfrac{v\ \sin \theta}{g} $

$\text{Height}$	$=vt\ \sin \theta-\dfrac{1}{2}gt^2 $
	$=\dfrac{v^2\sin^2 \theta}{g}-\dfrac{1}{2}g\Big{(} \dfrac{v^2\sin^2 \theta}{g^2}\Big{)} $
	$=\dfrac{v^2 \sin^2 \theta}{2g} $
	$=\dfrac{(2u)^2}{2g} $
	$=\dfrac{2u^2}{g} $
	$=H$

♦♦ Mean mark (iv) 34%.

Calculus, EXT1 C3 2023 HSC 13a

A hemispherical water tank has radius $R$ cm. The tank has a hole at the bottom which allows water to drain out.

Initially the tank is empty. Water is poured into the tank at a constant rate of $2 k R$ cm³ s$^{-1}$, where $k$ is a positive constant.

After $t$ seconds, the height of the water in the tank is $h$ cm, as shown in the diagram, and the volume of water in the tank is $V$ cm³.

It is known that $V= \pi \Big{(} R h^2-\dfrac{h^3}{3}\Big{)}. $ (Do NOT prove this.)

While water flows into the tank and also drains out of the bottom, the rate of change of the volume of water in the tank is given by $\dfrac{d V}{d t}=k(2 R-h)$.

Show that $\dfrac{d h}{d t}=\dfrac{k}{\pi h}$. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
Show that the tank is full of water after $T=\dfrac{\pi R^2}{2 k}$ seconds. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
The instant the tank is full, water stops flowing into the tank, but it continues to drain out of the hole at the bottom as before.
Show that the tank takes 3 times as long to empty as it did to fill. (3 marks)

--- 9 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{See Worked Solutions}$
$\text{See Worked Solutions}$
$\text{See Worked Solutions}$

Show Worked Solution

i. $V=\pi \Big{(}Rh^2-\dfrac{h^3}{3} \Big{)} $

$\dfrac{dV}{dh} = \pi(2Rh-h^2) $

$\dfrac{dV}{dt} = k(2R-h)\ \ \ \text{(given)} $

$\dfrac{dh}{dt}$	$= \dfrac{dV}{dt} \cdot \dfrac{dh}{dV} $
	$=k(2R-h) \cdot \dfrac{1}{\pi} \cdot \dfrac{1}{h(2R-h)} $
	$= \dfrac{k}{\pi h} $

ii. $\dfrac{dt}{dh} = \dfrac{\pi h}{k} $

$t$	$= \displaystyle \int \dfrac{dt}{dh}\ dh $
	$= \dfrac{\pi}{k} \displaystyle \int h\ dh $
	$= \dfrac{\pi}{k} \Big{[} \dfrac{h^2}{2} \Big{]} +c $

$\text{When}\ \ t=0, h=0 $

$\Rightarrow c=0 $

$ t= \dfrac{\pi h^2}{2k} $

$\text{Tank is full at time}\ T\ \text{when}\ \ h=R: $

$ T= \dfrac{\pi R^2}{2k}\ \text{seconds} $

♦ Mean mark (ii) 41%.

iii. $\text{Net water flow}\ = k(2R-h)\ \ \text{(given)} $

$\text{Flow in}\ =2kR\ \ \text{(given)} $

$\text{Flow out}\ = k(2R-h)-2kR=-kh $

$ \dfrac{dh}{dt}= \dfrac{-kh}{\pi h(2R-h)} = \dfrac{-k}{\pi (2R-h)} $

♦♦♦ Mean mark (iii) 20%.

$\dfrac{dt}{dh}$	$=\dfrac{- \pi (2R-h)}{k} $
$ \displaystyle \int k\ dt$	$=- \pi \displaystyle \int (2R-h)\ dh $
$kt$	$=- \pi \Big{(} 2Rh-\dfrac{h^2}{2} \Big{)}+c $

$\text{When}\ \ t=0, \ h=R: $

$0$	$=- \pi \Big{(}2R^2-\dfrac{R^2}{2} \Big{)} + c$
$c$	$= \pi \Big{(} \dfrac{3R^2}{2} \Big{)} $

$\text{Find}\ t\ \text{when}\ h=0: $

$kt$	$=- \pi(0) + \pi \dfrac{3R^2}{2} $
$t$	$= \dfrac{3 \pi R^2}{2k} $
	$= 3 \times \dfrac{\pi R^2}{2k} $

$\therefore\ \text{Tank takes 3 times longer to empty than fill.} $

Algebra, STD1 A3 2023 HSC 26

Electricity provider $A$ charges 25 cents per kilowatt hour (kWh) for electricity, plus a fixed monthly charge of $40.

Complete the table showing Provider $A$ 's monthly charges for different levels of electricity usage. (1 mark)

\begin{array} {|l|c|}
\hline
\rule{0pt}{2.5ex} \text{Electricity used in a month (kWh)} \rule[-1ex]{0pt}{0pt} & \ \ \ \ \ 0\ \ \ \ \ & \ \ \ 400\ \ \ & \ \ 1000\ \ \\
\hline
\rule{0pt}{2.5ex} \text{Monthly charge (\$)} \rule[-1ex]{0pt}{0pt} & 40 & & 290 \\
\hline
\end{array}

Provider $B$ charges 35 cents per kWh, with no fixed monthly charge. The graph shows how Provider $B$ 's charges vary with the amount of electricity used in a month.

On the grid on above, graph Provider A's charges from the table in part (a). (1 mark)
Use the two graphs to determine the number of kilowatt hours per month for which Provider $A$ and Provider $B$ charge the same amount. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
A customer uses an average of 800 kWh per month.
Which provider, $A$ or $B$, would be the cheaper option and by how much? (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

c. $400\text{ kWh}$

d. $A\text{ is cheaper by }$40.$

Show Worked Solution

♦♦ Mean mark (b) 40%.

c. $\text{Same charge when Provider }A = \text{Provider } B \text{ i.e. where the lines intersect}$

$=400\text{ kWh (see graph above)}$

d. $\text{When kWh}= 800, \ \ A=$240 \text{ and } B=$280$

$\therefore A\text{ is cheaper by }$40.$

Financial Maths, STD1 F2 2023 HSC 24

Bobby invested $5000.

The table shows the progress of his investment over the first 4 months.

What are the values of $A$ and $B$? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Bobby could have earned simple interest on the investment at 0.62% per month.
How much interest would Bobby have earned over 4 months by choosing this option? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $A=$30.54,\ \ B=$5121.08$

b. $$124$

Show Worked Solution

a.	$A$	$=5090.54\times\dfrac{0.6}{100}$
		$=$30.54\text{ (2 d.p.)}$

	$B$	$=5090.54+30.54$
		$=$5121.08$

b. $P=$5000,\ \ r=\dfrac{0.62}{100},\ \ n=4$

$I$	$=Prn$
	$=5000\times \dfrac{0.62}{100}\times 4$
	$=$124$

♦♦ Mean mark (b) 31%.

Financial Maths, STD1 F2 2023 HSC 21

An amount of $12 000 is invested in an account that pays 1 % interest per quarter, compounding quarterly for five years.

What is the future value of this investment? (3 marks)

Show Answers Only

$$14\ 642.28$

Show Worked Solution

$PV=$12\ 000,\ n=5\times 4=20, \ r=\dfrac{1}{100}$

$FV$	$=PV(1+r)^n$
	$=12\ 000 \Big(1+\dfrac{1}{100}\Big)^{20}$
	$=$14\ 642.28048$
	$\approx $14\ 642.28\text{ (2 d.p.)}$

♦ Mean mark 42%.

Statistics, STD1 S3 2023 HSC 19

The scatterplot shows the number of ice-creams sold, $y$, at a shop over a ten-day period, and the temperature recorded at 2 pm on each of these days.

The data are modelled by the equation of the line of best fit given below.

$y=0.936 x-8.929$, where $x$ is the temperature.

Sam used a particular temperature with this equation and predicted that 23 ice-creams would be sold.
What was the temperature used by Sam, to the nearest degree? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
In using the equation to make the prediction in part (a), was Sam interpolating or extrapolating? Justify your answer. (2 marks)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $34^{\circ}\text{ (nearest degree)}$

b. $\text{See worked solutions}$

Show Worked Solution

a. $y$	$=0.936x-8.929$
$23$	$=0.936x-8.929$
$0.936x$	$=23+8.929$
$x$	$=\dfrac{31.921}{0.936}$
	$=34.112\ldots ^{\circ}$
	$= 34^{\circ}\text{ (nearest degree)}$

♦♦ Mean mark (a) 31%.

b. $\text{Sam is extrapolating as 34°C is outside the range of data}$

$\text{points shown on the graph (i.e. temp between 0 and 30°C).}$

♦♦ Mean mark (b) 33%.

Measurement, STD1 M3 2023 HSC 16

From the top of a vertical cliff 120 metres high, a boat is observed. The angle of depression of the boat from the top of the cliff is 18°, as shown in the diagram.

Find the distance of the boat from the base of the cliff. Give your answer to the nearest metre. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

$369 \text{ m (nearest metre)}$

Show Worked Solution

$\text{Let }x\text{ be the distance from the cliff to the boat.}$

$\text{The angle at the boat}=18^{\circ}\text{ as it is alternate to the angle of depression from the cliff to the boat.}$

$\tan\theta$	$=\dfrac{\text{opp}}{\text{adj}}$
$\tan 18^{\circ}$	$=\dfrac{120}{x}$
$x$	$=\dfrac{120}{\tan 18^{\circ}}$
	$=369.322\ldots \text{m}$
	$\approx 369 \text{ m (nearest metre)}$

♦♦ Mean mark 30%.

Statistics, STD1 S1 2023 HSC 13

The graph shows the frequency of scores out of 10 awarded to a museum by visitors.

What is the mode of these data? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Describe TWO features of this graph. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $\text{Mode = Score with the highest frequency}=9$

b. $\text{Features could include any 2 of the following:}$

$\text{Data is negatively skewed as the mean and median are to the left of the mode}$
$\text{23 of the 24 scores, or 95.8%, are 5 or above.}$
$Q_2\text{(Median)}=8$
$Q_1=7\text{ and }Q_3=9$
$IQR=Q_1-Q_3=9-7=2$
$Q_1-1.5\times IQR=7-1.5\times 2=4\ \ \Rightarrow \ \ \text{1 is an outlier}$
$\text{Mean}=\dfrac{189}{24}=7.875$
$\text{If the outlier (1) was removed, Mean}=\dfrac{188}{23}=8.174\text{ (2 d.p.)}$

Show Worked Solution

a. $\text{Mode = Score with the highest frequency}=9$

b. $\text{Features could include any 2 of the following:}$

$\text{Data is negatively skewed as the mean and median are to the left of the mode}$
$\text{23 of the 24 scores, or 95.8%, are 5 or above.}$
$Q_2\text{(Median)}=8$
$Q_1=7\text{ and }Q_3=9$
$IQR=Q_1-Q_3=9-7=2$
$Q_1-1.5\times IQR=7-1.5\times 2=4\ \ \Rightarrow \ \ \text{1 is an outlier}$
$\text{Mean}=\dfrac{189}{24}=7.875$
$\text{If the outlier (1) was removed, Mean}=\dfrac{188}{23}=8.174\text{ (2 d.p.)}$

♦ Mean mark (a) 47%.
♦♦♦ Mean mark (b) 18%.

Measurement, STD1 M5 2023 HSC 12

A floor plan is shown.

What are the dimensions, in metres, of the living room? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
The shaded area of the kitchen floor is to be tiled. Each tile is 40 cm by 40 cm. How many tiles are needed to cover the kitchen floor? (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
The tiles are supplied in boxes of 10 . Only full boxes can be purchased. How many boxes need to be purchased to tile the kitchen floor? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $5.2\times 5.94$

b. $72\text{ tiles}$

c. $8\text{ boxes}$

Show Worked Solution

a. $\text{Dimensions}=5.2\times (2.15+0.16+3.6)=5.2\times5.94$

♦ Mean mark (a) 51%.

b. $\text{Method 1}$

$\text{Kitchen Area}$	$=3.2\times 3.6$
	$=11.52\text{ m}^2$
$\text{Tile area}$	$=0.4\times 0.4$
	$=0.16\text{ m}^2$
$\text{Tiles needed}$	$=\dfrac{11.52}{0.16}$
	$=72\text{ tiles}$

$\text{Method 2}$

$\text{Tiles to fit width}$	$=\dfrac{3.6}{0.4}$
	$=9$
$\text{Tiles to fit length}$	$=\dfrac{3.2}{0.4}$
	$=8$
$\text{Tiles needed}$	$=9\times 8$
	$=72\text{ tiles}$

♦ Mean mark (b) 43%.

c. $\text{Boxes}=\dfrac{72}{10}=7.2$

$\therefore\ \text{Boxes }=8$

Calculus, EXT1 C3 2023 HSC 12e

The region, $R$, bounded by the hyperbola $y=\dfrac{60}{x+5}$, the line $x=10$ and the coordinate axes is shown.

Find the volume of the solid of revolution formed when the region $R$ is rotated about the $y$-axis. Leave your answer in exact form. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

$V=1200 \pi-600\pi\ \ln3 \ \ \text{u}^3$

Show Worked Solution

$y=\dfrac{60}{x+5}\ \ \Rightarrow\ \ x=\dfrac{60}{y}-5 $

♦ Mean mark 49%.

$V$	$=\pi \displaystyle \int_4^{12} x^2\ dy + \pi r^2h$
	$=\pi \displaystyle \int_4^{12} \Big{(} \dfrac{60}{y}-5 \Big{)}^2 \ dy + \pi \times 10^2 \times 4 $
	$=\ 25\pi \displaystyle \int_4^{12} \Big{(} \dfrac{12}{y}-1 \Big{)}^2 \ dy + 400\pi $
	$=\ 25\pi \displaystyle \int_4^{12} \Big{(} \dfrac{144}{y^2}-\dfrac{24}{y} + 1 \Big{)} \ dy + 400\pi $
	$=\ 25\pi \Big{[} \dfrac{-144}{y}- 24 \ln y + y\Big{]}_4^{12} + 400\pi $
	$=\ 25\pi \Big{[} (-12-24 \ln 12 +12)-(-36-24 \ln 4+4)\Big{]} + 400\pi $
	$=\ 25\pi (24 \ln 4-24 \ln 12+32) + 400\pi $
	$=600 \pi\ \ln(3^{-1}) + 800 \pi + 400 \pi $
	$=1200 \pi-600\pi\ \ln3 \ \ \text{u}^3$

Measurement, STD1 M4 2023 HSC 10 MC

A tap is dripping at the rate of 4 mL per minute.

Which expression shows how many litres this would amount to in one year?

$\dfrac{4 \times 1000}{60 \times 24 \times 365}$
$\dfrac{4 \times 60 \times 24 \times 365}{1000}$
$\dfrac{60 \times 24 \times 365}{4 \times 1000}$
$\dfrac{1000}{4 \times 60 \times 24 \times 365}$

Show Answers Only

$B$

Show Worked Solution

$\text{Rate}\Rightarrow 4 \text{ mL} / \text{minute}$

$\text{Litres in 1 year}$	$=\dfrac{4}{1000}\times 60\times 24\times365$
	$=\dfrac{4 \times 60 \times 24 \times 365}{1000}$

$\Rightarrow B$

♦ Mean mark 47%.

Measurement, STD1 M5 2023 HSC 9 MC

A bag contains 150 jelly beans. Some of them are red and the rest are blue. The ratio of red to blue jelly beans is 2 : 3.

Sophie eats 10 of each colour.

What is the new ratio of red to blue jelly beans?

$2 : 3$
$4 : 9$
$5 : 8$
$11 : 17$

Show Answers Only

$C$

Show Worked Solution

$\text{Original ratio}\ = 2:3$

$\text{5 parts = 150}\ \Rightarrow\ \text{1 part}\ = 150/5=30$

$\text{Original ratio (by number)}\ = 2 \times 30:3 \times 30 = 60:90$

$\text{After eating 10 of each colour:}$

$\text{Ratio}\ = 50:80 = 5:8$

$\Rightarrow C$

♦♦ Mean mark 34%.

Algebra, STD1 A3 2023 HSC 4 MC

The diagram shows water in a pool which is in the shape of a triangular prism. The pool is being emptied of water at a constant rate.

Which graph best illustrates the change in depth of water with time?

Show Answers Only

$D$

Show Worked Solution

$\text{Eliminate B and C as water depth decreases with time.}$

$\text{Eliminate A as rate of flow out of the tank is not linear.}$

$\Rightarrow D$

♦ Mean mark 49%.

Measurement, STD1 M5 2023 HSC 3 MC

Two towns are $5$ cm apart on a map that uses a scale of $1 : 100\ 000$.

What is the actual distance between the two towns?

$5\text{ km}$
$50\text{ km}$
$500\text{ km}$
$5000\text{ km}$

Show Answers Only

$A$

Show Worked Solution

$5\text{ cm : }$	$ 500\ 000\text{ cm}$
$5\text{ cm : }$	$ 5000\text{ m}$
$5\text{ cm : }$	$ 5\text{ km}$

$\Rightarrow A$

♦ Mean mark 23%.

Functions, EXT1 F1 2023 HSC 9 MC

The graph of a cubic function, $y=f(x)$, is given below.

Which of the following functions has an inverse relation whose graph has more than 3 points with an $x$-coordinate of 1 ?

$y=\sqrt{f(x)}$
$y=\dfrac{1}{f(x)}$
$y=f(|x|)$
$y=|f(x)|$

Show Answers Only

$D$

Show Worked Solution

$\text{An inverse function with more than 3 points when}\ \ x=1\ \ \text{is the same}$

$\text{as the original function intersecting}\ \ y=1\ \ \text{more than 3 times.}$

$\text{Consider}\ \ y=|f(x)| : $

$ y=1\ \ \text{cuts}\ \ y=f(x)\ \text{three times and}\ \ y=|f(x)|\ \ \text{four times} $

$\text{as the graph below the x-axis (bottom right) is reflected in the axis.}$

$\Rightarrow D$

♦ Mean mark 47%.

Vectors, EXT1 V1 2023 HSC 6 MC

Given the two non-zero vectors $\underset{\sim}{a}$ and $\underset{\sim}{b}$, let $\underset{\sim}{c}$ be the projection of $\underset{\sim}{a}$ onto $\underset{\sim}{b}$.

What is the projection of $10 \underset{\sim}{a}$ onto $2 \underset{\sim}{b}$ ?

$2 \underset{\sim}{c}$
$5 \underset{\sim}{c}$
$10 \underset{\sim}{c}$
$20 \underset{\sim}{c}$

Show Answers Only

$C$

Show Worked Solution

$\underset{\sim}c=\text{proj}_{\underset{\sim}b}\underset{\sim}a =\dfrac{\underset{\sim}a \cdot \underset{\sim}b}{|b|^2} \underset{\sim}b $

♦ Mean mark 49%.

$\text{proj}_{2\underset{\sim}b} 10\underset{\sim}a $	$=\dfrac{10\underset{\sim}a \cdot 2\underset{\sim}b}{\big{\|}2\underset{\sim}b\big{\|}^2} 2\underset{\sim}b $
	$=\dfrac{20 \times 2}{2^2} \Bigg{(}\dfrac{\underset{\sim}a \cdot \underset{\sim}b}{\|\underset{\sim}b\|^2} \underset{\sim}b \Bigg{)} $
	$=10 \underset{\sim}c $

$\Rightarrow C$

Calculus, 2ADV C3 2023 HSC 30

Let $f(x)=e^{-x} \sin x$.

Find the coordinates of the stationary points of $f(x)$ for $0\leq x\leq 2\pi$. You do NOT need to check the nature of the stationary points. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Without using any further calculus, sketch the graph of $y=f(x)$, for $0\leq x\leq 2\pi$, showing stationary points and intercepts. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $ \Big(\dfrac{\pi}{4},\dfrac{1}{\sqrt2 \times e^{\frac{\pi}{4}}}\Big)\ \text{and}\ \Big(\dfrac{5\pi}{4},\dfrac{-1}{\sqrt2 \times e^{\frac{5\pi}{4}}}\Big)$

Show Worked Solution

a. $f(x)=e^{-x} \sin x$

$f^{′}(x)=e^{-x} \cos x-e^{-x} \sin x = e^{-x}( \cos x-\sin x) $

$\text{SPs when}\ f^{′}(x)=0: $

$e^{-x}=0\ \ \rightarrow \ \text{no solution} $

$\cos x-\sin x$	$=0$
$1-\tan x$	$=0$
$\tan$	$=1$

Mean mark (a) 54%.

$x=\dfrac{\pi}{4}, \dfrac{5\pi}{4} $

$f(\dfrac{\pi}{4})=e^{-\frac{\pi}{4}}\sin \frac{\pi}{4}=\dfrac{1}{\sqrt2 \times e^{\frac{\pi}{4}}} $

$f(\dfrac{5\pi}{4})=e^{-\frac{5\pi}{4}}\sin \frac{5\pi}{4}=\dfrac{-1}{\sqrt2 \times e^{\frac{5\pi}{4}}} $

$\therefore\ \text{SPs at}\ \Big(\dfrac{\pi}{4},\dfrac{1}{\sqrt2 \times e^{\frac{\pi}{4}}}\Big)\ \text{and}\ \Big(\dfrac{5\pi}{4},\dfrac{-1}{\sqrt2 \times e^{\frac{5\pi}{4}}}\Big)$

b. $\ x\text{-intercepts at}\ \ x=0, \pi,\ 2\pi $

♦♦ Mean mark (b) 34%.

Probability, 2ADV S1 2023 HSC 31

Four Year 12 students want to organise a graduation party. All four students have the same probability, $P(F)$, of being available next Friday. All four students have the same probability, $P(S)$, of being available next Saturday.

It is given that $P(F)=\dfrac{3}{10}, P(S\mid F)=\dfrac{1}{3}$, and $P(F\mid S)=\dfrac{1}{8}$.

Kim is one of the four students.

Is Kim's availability next Friday independent from his availability next Saturday? Justify your answer. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Show that the probability that Kim is available next Saturday is $\dfrac{4}{5}$. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---
What is the probability that at least one of the four students is NOT available next Saturday? (2 marks)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $P(F) \neq P(F|S)\ \text{which is not the case}\ \ (\dfrac{3}{10} \neq \dfrac{1}{8}) $

$\therefore\ \text{Kim’s availability on Friday is not independent of Saturday}$

b. $\text{See Worked Solutions} $

c. $\dfrac{369}{625} $

Show Worked Solution

a. $P(F) \neq P(F|S)\ \text{which is not the case}\ \ (\dfrac{3}{10} \neq \dfrac{1}{8}) $

$\therefore\ \text{Kim’s availability on Friday is not independent of Saturday}$

♦♦♦ Mean mark (a) 18%.

b.	$P(S\|F) $	$= \dfrac{P(S) \cap P(F)}{P(F)} $
	$\dfrac{1}{3}$	$= \dfrac{P(S) \cap P(F)}{\frac{3}{10}} $
	$\dfrac{1}{10}$	$=P(S) \cap P(F) $

♦ Mean mark (b) 44%.

$P(F\|S)$	$= \dfrac{P(F) \cap P(S)}{P(S)} $
$\dfrac{1}{8}$	$=\dfrac{\frac{1}{10}}{P(S)} $
$\dfrac{1}{8} \times P(S) $	$=\dfrac{1}{10} $
$P(S)$	$=\dfrac{4}{5} $

c.	$P\text{(at least 1 not available)}$	$=1-P\text{(all are available)} $
		$=1-\left(\dfrac{4}{5}\right)^4 $
		$=\dfrac{369}{625} $

♦♦ Mean mark (c) 34%.

Statistics, 2ADV S3 2023 HSC 29

A continuous random variable $X$ has probability density function $f(x)$ given by

$f(x)=\left\{\begin{array}{cl} 12 x^2(1-x), & \text { for } 0 \leq x \leq 1 \\ 0, & \text { for all other values of } x \end{array}\right.$

Find the mode of $X$. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
Find the cumulative distribution function for the given probability density function. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
Without calculating the median, show that the mode is greater than the median. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $x=\dfrac{2}{3} $

b. $F(x)=\left\{\begin{array}{cl} 0, & \text { for } x \lt 0 & \\ 4x^3-3x^4, & \text { for } 0 \leq x \leq 1 \\ 1, & \text { for } x > 1 \end{array}\right.$

c. $\text{See Worked Solutions}$

Show Worked Solution

a. $\text{Mode}\ \rightarrow \ f(x)_\text{max} $

$f(x)=12 x^2(1-x)=12x^2-12x^3 $

$f^{′}(x)=24x-36x^2=12x(2-3x) $

$f^{″}(x)=24-72x $

♦ Mean mark (a) 45%.

$\text{Max/min when}\ f^{′}(x)=0 $

$2-3x=0\ \ ⇒\ \ x=\dfrac{2}{3} \ \ (x \neq 0) $

$\text{At}\ x=\dfrac{2}{3}, \ f^{″}(x)=24-72(\dfrac{2}{3})=-24<0 $

$\therefore \ \text{Mode (max) at}\ x=\dfrac{2}{3} $

b.	$F(x)$	$= \int 12x^2-12x^3\ dx$
		$=4x^3-3x^4+c $

$\text{At}\ x=0, F(x)=0\ \ ⇒\ \ c=0 $

$F(x)=4x^3-3x^4 $

$F(x)=\left\{\begin{array}{cl} 0, & \text { for } x \lt 0 & \\ 4x^3-3x^4, & \text { for } 0 \leq x \leq 1 \\ 1, & \text { for } x > 1 \end{array}\right.$

c. $\text{Find}\ F\Big{(}\dfrac{2}{3}\Big{)}: $

$F\Big{(}\dfrac{2}{3}\Big{)} $	$=4 \times \Big{(}\dfrac{2}{3}\Big{)}^3-3 \times \Big{(}\dfrac{2}{3}\Big{)}^4 $
	$=\dfrac{16}{27}>0.5 $

$\therefore\ \text{Mode > median}$

♦♦♦ Mean mark (c) 17%.

Calculus, 2ADV C4 2023 HSC 28

The curve $y=f(x)$ is shown on the diagram. The equation of the tangent to the curve at point $T(-1,6)$ is $y=x+7$. At a point $R$, another tangent parallel to the tangent at $T$ is drawn.

The gradient function of the curve is given by $\dfrac{dy}{dx}=3x^2-6x-8$.

Find the coordinates of $R$. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

$R(3,-22)$

Show Worked Solution

$\text{Gradient at}\ R=1:$

$3x^2-6x-8$	$=1$
$3x^2-6x-9$	$=0$
$3(x^2-2x-3$	$=0$
$3(x+1)(x-3)$	$=0$

♦ Mean mark 51%.

$x\text{-coordinate of}\ R = 3$

$y$	$=\int 3x^2-6x-8\ dx$
	$=x^3-3x^2-8x+c$

$\text{Graph passes through}\ (-1,6):$

$6$	$=-1-3+8+c$
$c$	$=2$

$y=x^3-3x^2-8x+2$

$\text{When}\ x=3:$

$y=27-27-24+2=-22$

$\therefore R(3,-22)$

Calculus, 2ADV C4 2023 HSC 26

A camera films the motion of a swing in a park.

Let $x(t)$ be the horizontal distance, in metres, from the camera to the seat of the swing at $t$ seconds.

The seat is released from rest at a horizontal distance of 11.2 m from the camera.

The rate of change of $x$ can be modelled by the equation

$\dfrac{dx}{dt}=-1.5\pi\ \sin(\dfrac{5\pi}{4}t)$.

Find an expression for $x(t)$. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
How many times does the swing reach the closest point to the camera during the first 10 seconds? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

$x(t)=\dfrac{6}{5} \cos(\dfrac{5\pi}{4}t) + 10$
$\text{6 times}$

Show Worked Solution

a. $\dfrac{dx}{dt}=-1.5\pi\ \sin(\dfrac{5\pi}{4}t)$

$x(t)$	$= -1.5\pi\ \int \sin(\dfrac{5\pi}{4}t)\ dt $
	$= 1.5\pi \times \dfrac{4}{5\pi} \times \cos(\dfrac{5\pi}{4}t) + c$
	$=\dfrac{6}{5} \cos(\dfrac{5\pi}{4}t) + c $

Mean mark (a) 51%.

$\text{When}\ t=0, \ x(t)=11.2:$

$11.2$	$=\dfrac{6}{5} \cos(0) + c$
$c$	$=11.2-\dfrac{6}{5} $
	$=10$

$x(t)=\dfrac{6}{5} \cos(\dfrac{5\pi}{4}t) + 10$

b. $\text{Period}\ =\dfrac{2\pi}{n} = \dfrac{2\pi}{\frac{5\pi}{4}} = \dfrac{8}{5} = 1.6\ \text{(seconds)}$

♦♦ Mean mark (b) 31%.

$\text{1st time swing reaches closest point to camera = 0.8 seconds}$

$\text{Periods in next 9.2 seconds}$	$=\dfrac{9.2}{1.6}$
	$= 5.75\ \text{times}$

$\therefore\ \text{Swing reaches the closest point 6 times in the 1st 10 seconds}$

Financial Maths, 2ADV M1 2023 HSC 25

On the first day of November, Jia deposits $10 000 into a new account which earns 0.4% interest per month, compounded monthly. At the end of each month, after the interest is added to the account, Jia intends to withdraw $$M$ from the account.

Let $A_n$ be the amount (in dollars) in Jia's account at the end of $n$ months.

Show that $A_2 = 10\ 000(1.004)^2-M(1.004)-M$. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Show that $A_n = (10\ 000-250M)(1.004)^n + 250M$. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---
Jia wants to be able to make at least 100 withdrawals.
What is the largest value of $M$ that will enable Jia to do this? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{See Worked Solutions}$
$\text{See Worked Solutions}$
$$121.52$

Show Worked Solution

a. $A_1=10\ 000(1.004)-M$

$A_2$	$=A_1(1.004)-M$
	$=[(10\ 000(1.004)-M)](1.004)-M$
	$=10\ 000(1.004)^2-M(1.004)-M$

b. $A_3=10\ 000(1.004)^3-M(1.004)^2-M(1.004)-M$

$ \vdots$

♦ Mean mark (b) 44%.

$A_n$	$=10\ 000(1.004)^n-M(1.004)^{n-1}-…-M(1.004)-M$
	$=10\ 000(1.004)^n-M \underbrace{(1+1.004+1.004^2+…+1.004^{n-1})}_{\text{GP where}\ a=1, r=1.004, n=n} $

$A_n$	$=10\ 000(1.004)^n-M(\dfrac{1.004^n-1}{1.004-1}) $
	$=10\ 000(1.004)^n-M(\dfrac{1.004^n-1}{0.004}) $
	$=10\ 000(1.004)^n-250M(1.004^n-1) $
	$=10\ 000(1.004)^n-250M(1.004)^n+250M $
	$=(10\ 000-250M)(1.004)^n + 250M$

c. $\text{Find}\ M\ \text{when}\ A_{100}=0: $

$A_{100}$	$= (10\ 000-250M)(1.004)^{100}+250M$
$0$	$=10\ 000(1.004)^{100}-250M(1.004)^{100}+250M $

$250M(1.004^{100}-1)$	$=10\ 000(1.004)^{100} $
$M$	$=\dfrac{10\ 000(1.004)^{100}}{250(1.004^{100}-1)} $
	$=121.527…$

$ \therefore M_\text{max} = $121.52$

Mean mark (c) 53%.

Calculus, 2ADV C3 2023 HSC 24

A gardener wants to build a rectangular garden of area 50 m² against an existing wall as shown in the diagram. A concrete path of width 1 metre is to be built around the other three sides of the garden.

Let $x$ and $y$ be the dimensions, in metres, of the outer rectangle as shown.

Show that $y$ = $\dfrac {50}{x - 2}+1 $. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Find the value of $x$ such that the area of the concrete path is a minimum. Show that your answer gives a minimum area. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{See worked solutions}$
$x=12$

Show Worked Solution

a.	$ (y-1)(x-2)$	$=50$
	$yx-2y-x+2$	$=50$
	$y(x-2)$	$=48+x$
	$y$	$=\dfrac{48+x}{x-2}$
	$y$	$=\dfrac{50+(x-2)}{x-2}$
	$y$	$=\dfrac{50}{x-2}+1$

b. $\text{Let}\ A=\ \text{area of concrete path}$

$A$	$= xy-50$
	$= x(\dfrac{50}{x-2}+1)-50$
	$=\dfrac{50x}{x-2}+x-50$

$\dfrac{dA}{dx}$	$=\dfrac{50(x-2)-50x}{(x-2)^2}+1$
	$=\dfrac{-100}{(x-2)^2}+1$

$\text{Max/min when}\ \dfrac{dA}{dx}=0$

$\dfrac{-100}{(x-2)^2}+1$	$=0$
$(x-2)^2$	$=100$
$x-2$	$=\pm 10$

$x=12\ \ (x>0)$

♦♦ Mean mark (b) 33%.

$\text{Check gradients about}\ \ x=12: $

\begin{array} {|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} x \rule[-1ex]{0pt}{0pt} & 10 & 12 & 14\\
\hline
\rule{0pt}{2.5ex}\dfrac{dA}{dx} \rule[-1ex]{0pt}{0pt} & – \frac{9}{16} & 0 & \frac{11}{36}\\
\rule{0pt}{2.5ex} \rule[-1ex]{0pt}{0pt} & \text{ \ } & \text{ _ } & \text{ / } \\
\hline
\end{array}

$\therefore \text{Minimum at}\ x=12.$

Calculus, 2ADV C1 2023 HSC 7 MC

It is given that `y=f(g(x))`, where `f(1)=3`, `f^{′}(1)=-4`, `g(5)=1` and `g^{′}(5)=2`.

What is the value of `y^{′}` at `x=5`?

`-8`
`-4`
`3`
`6`

Show Answers Only

`A`

Show Worked Solution

`y`	`=f(g(x))`
`y^{′}`	`=f^{′}(g(5)) xx g^{′}(5)`
	`=f^{′}(1) xx 2`
	`=-4xx2`
	`=-8`

`=>A`

♦♦ Mean mark 38%.

Calculus, 2ADV C4 2023 HSC 5 MC

The diagram shows the graph `y=f(x)`, where `f(x)` is an odd function.

The shaded area is 1 square unit.

The number `a`, where `a > 1`, is chosen so that `int_0^a f(x)\ dx=0`.

What is the value of `int_{-a}^1 f(x)\ dx` ?

`-1`
`0`
`1`
`3`

Show Answers Only

`A`

Show Worked Solution

`text{Since}\ \ int_0^a f(x)\ dx=0\ and \ int_0^1 f(x)\ dx=-1\ \ text{(given)}`

`int_1^a f(x)\ dx=1`

`:. int_{-a}^{-1} f(x)\ dx=-1\ \ text{(f(x) is odd)}`

`:. int_{-a}^1 f(x)\ dx=-1`

`=>A`

♦ Mean mark 49%.

Statistics, STD2 S5 2023 HSC 38

A random variable is normally distributed with a mean of 0 and a standard deviation of 1 . The table gives the probability that this random variable lies below `z` for some positive values of `z`.

The probability values given in the table are represented by the shaded area in the following diagram.

The weights of adult male koalas form a normal distribution with mean `mu` = 10.40 kg, and standard deviation `sigma` = 1.15 kg.

In a group of 400 adult male koalas, how many would be expected to weigh more than 11.93 kg? (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`37\ text{koalas*}`

`text{*36 or 36.72 koalas would also receive full marks}`

Show Worked Solution

`ztext{-score (11.93)}`	`=(x-mu)/sigma`
	`=(11.93-10.4)/1.15`
	`=1.330`

`Ptext{(Koala weighs > 11.93 kg)}\ = P(z>1.330)`

`text{Using the table:}`

`P(z>1.33)`	`=1-0.9082`
	`=0.0918`

♦ Mean mark 39%.

`:.\ text{Expected koalas > 11.93 kg}`	`=0.0918 xx 400`
	`=36.72`
	`=37\ text{koalas*}`

`text{*36 or 36.72 koalas would also receive full marks}`

Statistics, STD2 S4 2023 HSC 34

A university uses gas to heat its buildings. Over a period of 10 weekdays during winter, the gas used each day was measured in megawatts (MW) and the average outside temperature each day was recorded in degrees Celsius (°C).

Using `x` as the average daily outside temperature and `y` as the total daily gas usage, the equation of the least-squares regression line was found.

The equation of the regression line predicts that when the temperature is 0°C, the daily gas usage is 236 MW.

The ten temperatures measured were: 0°, 0°, 0°, 2°, 5°, 7°, 8°, 9°, 9°, 10°,

The total gas usage for the ten weekdays was 1840 MW.

In any bivariate dataset, the least-squares regression line passes through the point `(bar x,bar y)`, where `bar x` is the sample mean of the `x`-values and `bary` is the sample mean of the `y`-values.

Using the information provided, plot the point `(bar x,bar y)` and the `y`-intercept of the least-squares regression line on the grid. (3 marks)

What is the equation of the regression line? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
In the context of the dataset, identify ONE problem with using the regression line to predict gas usage when the average outside temperature is 23°C. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Show Answers Only

b. `y=-10.4x+236`

c. `text{Answers could include one of the following:}`

`text{→ 23°C is outside the range of the dataset and requires the trend}`

`text{to be extrapolated.}`

`text{→ At 23°C, the equation predicts negative daily gas usage.}`

Show Worked Solution

a. `barx=(0+0+0+2+5+7+8+9+9+10)/10=5^@text{C}`

`bary=1840/10=184`

`text{Regression line passes through:}\ (0,236) and (5,184)`

♦ Mean mark (a) 44%.

b. `m=(y_2-y_1)/(x_2-x_1)=(184-236)/(5-0)=-10.4`

`text{Equation of line}\ m=-10.4\ text{passing through}\ (0,236):`

`(y-y_1)`	`=m(x-x_1)`
`y-236`	`=-10.4(x-0)`
`y`	`=-10.4x+236`

♦♦♦ Mean mark (b) 21%.

c. `text{Answers could include one of the following:}`

`text{→ 23°C is outside the range of the dataset and requires the trend}`

`text{to be extrapolated.}`

`text{→ At 23°C, the equation predicts negative daily gas usage.}`

♦♦♦ Mean mark 23%.

Measurement, STD2 M6 2023 HSC 33

The diagram shows a shape `APQBCD`. The shape consists of a rectangle `ABCD` with an arc `PQ` on side `AB` and with side lengths `BC` = 3.6 m and `CD` = 8.0 m.

The arc `PQ` is an arc of a circle with centre `O` and radius 2.1 m and `∠POQ=110°`.

What is the perimeter of the shape `APQBCD`? Give your answer correct to one decimal place. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

`23.8\ text{m}`

Show Worked Solution

`text{Arc}\ PQ`	`=110/360 xx pi xx 2.1^2`
	`=4.03171… \ text{m}`

`text{Consider}\ ΔOPQ:`

♦ Mean mark 42%.

`sin 55^@`	`=x/2.1`
`x`	`=2.1 xx sin 55^@`
	`=1.7202…`

`PQ=2x=3.440\ text{m}`

`:.\ text{Perimeter}`	`=8+(2xx3.6)+4.031+(8-3.440)`
	`=23.79…`
	`=23.8\ text{m (to 1 d.p.)}`

Financial Maths, STD2 F4 2023 HSC 32

Ali has a credit card which has no interest-free period. Interest is charged at 13.5% per annum, compounding daily, on the amount owing.

During the month, Ali made only one purchase of $450 using the credit card. The full amount owing was repaid 21 days later.

Calculate the amount of interest charged on the purchase, assuming that interest is charged for the 21 days. (2 marks)
What percentage of the full amount repaid is the interest? Give the answer to two decimal places. (2 marks)

Show Answers Only

`$3.51`
`0.77%`

Show Worked Solution

a. `text{Daily interest rate}\ (r) = 13.5/365 % = 0.135/365`

`n=\ text{21 days}`

`FV`	`=PV(1+r)^n`
	`=450(1+0.135/365)^21`
	`=$453.51`

`:.\ text{Interest charged}\ = 453.51-450=$3.51`

♦ Mean mark (a) 45%.

b.	`text{Interest as % total repaid}`	`=3.51/453.51 xx 100`
		`=0.007739…`
		`=0.77%\ text{(to 2 d.p.)}`

♦ Mean mark (b) 49%.

Networks, STD2 N3 2023 HSC 31

A function centre employs staff so that all necessary tasks can be completed between the end of one function and the beginning of the next function.

The network diagram shows the time taken in hours for the tasks that need to be completed.

Find the TWO critical paths. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
The function centre wants to decrease the length of each critical path by 3 hours. They can do this by hiring more staff to do ONE of the tasks so it takes less time to complete.
For which task should the centre hire more staff, and how long should that task take to ensure all tasks can be completed in 14 hours? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. `HIGC and HIK`

b. `text{More staff should be hired for task}\ I.`

`text{By decreasing task}\ I\ text{by 3 hours (so it takes 4 hours), the}`

`text{critical path of the network reduces to 14 hours.}`

Show Worked Solution

a. `text{Scanning both ways:}`

`text{Critical paths:}\ HIGC and HIK`

♦ Mean mark (a) 46%.

b. `text{More staff should be hired for task}\ I.`

`text{By decreasing task}\ I\ text{by 3 hours (so it takes 4 hours), the}`

`text{critical path of the network reduces to 14 hours.}`

Mean mark (b) 52%.

Financial Maths, STD2 F1 2023 HSC 30

A receipt from a supermarket shows a total of $124.87. The GST shown on the receipt is $3.86.

GST, at a rate of 10%, is only charged on some items.

What was the value of the items which did NOT have GST charged? (3 marks)

Show Answers Only

`$82.41`

Show Worked Solution

`text{Let}\ X=\ text{cost of goods that attract GST (before GST added)}`

`10% xx X`	`=3.86`
`X`	`=$38.60\ \ text{(before GST added)}`

`text{Items with no GST}`	`=124.87-38.60-3.86`
	`=$82.41`

♦ Mean mark 46%.

Financial Maths, STD2 F4 2023 HSC 29

The table shows monthly repayments for each $1000 borrowed.

A couple borrows $520 000 to buy a house at 8% per annum over 25 years.
How much does the couple repay in total for this loan? (3 marks)

--- 7 WORK AREA LINES (style=lined) ---
Chris borrows some money at 7% per annum. Chris will repay the loan over 15 years, paying $3596 per month.
How much money does Chris borrow? (1 mark)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

`$1\ 204\ 320`
`400\ 000`

Show Worked Solution

a. `text{8.0% interest over a 25 year loan}`

`text{Monthly repayments to borrow $1000 = $7.72}`

`text{Total months}\ = 25 xx 12 = 300`

`text{Monthly repayments}`	`=520 xx 7.72`
	`=$4014.40`

`:.\ text{Total repayments}`	`= 4014.40 xx 300`
	`=$1\ 204\ 320`

♦ Mean mark (a) 50%.

b. `text{7.0% interest over a 15 year loan}`

`text{Monthly repayments to borrow $1000 = $8.99}`

`:.\ text{Amount borrowed}`	`=3596/8.99 xx $1000`
	`=400\ 000`

♦♦♦ Mean mark (b) 11%.

Measurement, STD2 M6 2023 HSC 27

The diagram shows the location of three places `X`, `Y` and `C`.

`Y` is on a bearing of 120° and 15 km from `X`.

`C` is 40 km from `X` and lies due west of `Y`.

`P` lies on the line joining `C` and `Y` and is due south of `X`.

Find the distance from `X` to `P`. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
What is the bearing of `C` from `X`, to the nearest degree? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

`7.5\ text{km}`
`259^@`

Show Worked Solution

a. `text{In}\ ΔXPY:`

`anglePXY=180-120=60^@`

`cos 60^@`	`=(XP)/15`
`XP`	`=15 xx cos 60^@`
	`=7.5\ text{km}`

b. `text{In}\ ΔXPC:`

`text{Let}\ \ theta = angleCXP`

`cos theta`	`=7.5/40`
`theta`	`=cos^{-1}(7.5/40)`
	`=79.193…`
	`=79^@\ \ text{(nearest degree)}`

`text{Bearing}\ C\ text{from}\ X`	`=180+79`
	`=259^@`

♦ Mean mark (b) 39%.

Measurement, STD2 M1 2023 HSC 24

The diagram shows the cross-section of a wall across a creek.

Use two applications of the trapezoidal rule to estimate the area of the cross-section of the wall. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
The wall has a uniform thickness of 0.80 m. The weight of 1 m³ of concrete is 3.52 tonnes.
How many tonnes of concrete are in the wall? Give the answer to two significant figures. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

`18\ text{m}^2`
`text{51 tonnes}`

Show Worked Solution

a. `h=8.0/2=4`

`A`	`~~h/2[1.9+1.7+2(2.7)]`
	`~~4/2(9)`
	`~~18\ text{m}^2`

b. `V_text{wall}=18 xx 0.8=14.4\ text{m}^3`

`text{Mass of concrete}`	`=14.4 xx 3.52`
	`=50.688`
	`=51\ text{tonnes (2 sig.fig.)}`

♦ Mean mark (b) 46%.

Networks, STD2 N2 2023 HSC 19

A network of running tracks connects the points `A, B, C, D, E, F, G, H`, as shown. The number on each edge represents the time, in minutes, that a typical runner should take to run along each track.

Which path could a typical runner take to run from point `A` to point `D` in the shortest time? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
A spanning tree of the network above is shown.
Is it a minimum spanning tree? Give a reason for your answer. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. `ABFGD`

b. `text{See worked solutions}`

Show Worked Solution

a. `text{Using Djikstra’s Algorithm:}`

`text{Shortest route}`	`=ABFGD`
	`=3+1+5+5`
	`=14`

b. `text{Total time of given spanning tree}`

`=3+11+1+2+4+5+5`

`=31`

`text{Consider the MST below:}`

`text{Total time (MST)}\ = 3+1+2+4+5+5+9=29`

`:.\ text{Given tree is NOT a MST.}`

♦ Mean mark (b) 47%.

Statistics, STD2 S5 2023 HSC 18

The histogram shows a summary of scores on a test.

Provide TWO features of the histogram that indicate that the data comes from a normal distribution. (2 marks)

Show Answers Only

`text{Choose two from the following features:}`

- `text{Data distribution is symmetrical about the mean}`
- `text{Mean = median = mode}`
- `text{Histogram has only a single peak}`

Show Worked Solution

`text{Choose two from the following features:}`

- `text{Data distribution is symmetrical about the mean}`
- `text{Mean = median = mode}`
- `text{Histogram has only a single peak}`

♦♦ Mean mark 31%.

Statistics, STD2 S1 2023 HSC 15 MC

Ashan's mathematics class needs to complete six tests, each worth 100 marks.

After completing the first five tests, Ashan calculated that he would need a mark of 90 in the final test in order to have a mean mark of 80 for the six tests.

What was Ashan's mean mark after completing the first five tests?

Show Answers Only

`A`

Show Worked Solution

`text{Total marks after 6 tests}\ = 80xx6=480`

`text{Actual marks after 5 tests}\ = 480-90=390`

`text{Average after 5 tests}\ = 390/5=78`

`=>A`

♦ Mean mark 40%.

Networks, STD2 N3 2023 HSC 14 MC

A network with source `A` and sink `B` is shown. The capacities of two paths are labelled. The cut shown on the diagram has a capacity of 30 .

Which of the following statements is correct?

The maximum flow is 30.
The maximum flow is 35.
The maximum flow is 30 or less.
The maximum flow is 30 or more.

Show Answers Only

`C`

Show Worked Solution

`text{The cut shows a maximum flow of 30, however there is no information}`

`text{that it is the minimum cut across the network}`

`text{(i.e. it is possible the minimum cut is lower than 30).}`

`=>C`

♦♦ Mean mark 33%.

Financial Maths, STD2 F1 2023 HSC 13 MC

An item is discounted by 30% and then a further discount of 20% is applied to the reduced price.

What is the total percentage discount?

Show Answers Only

`=>B`

Show Worked Solution

`text{Method 1}`

`text{Let original price}\ =x`

`text{1st discount}\ =0.7x`

`text{2nd discount}\ = 0.7x xx 0.8=0.56x`

`text{Total discount}\ = 1-0.56=0.44`

♦♦ Mean mark 47%.

`text{Method 2}`

`text{$100 less 30% = $70}`

`text{$70 less 20%} = 70-0.2xx70=$56`

`text{Total discount $100 ↓ $56 = 44%}`

`=>B`

Measurement, STD2 M6 2023 HSC 12 MC

A cylindrical pipe with a radius of 12.5 cm is filled with water to a depth, `d` cm, as shown.

The surface of the water has a width of 20 cm.

What is the depth of water in the pipe?

2.5 cm
5.0 cm
7.5 cm
12.5 cm

Show Answers Only

`B`

Show Worked Solution

`text{Triangle base}\ = 20/2=10\ text{cm}`

`text{Let}\ x =\ text{⊥ distance from centre to water}`

`text{Using Pythagoras:}`

`12.5^2`	`=x^2+10^2`
`x^2`	`=12.5^2-10^2`
	`=56.25`
`x`	`=7.5\ text{cm}`

`d=12.5-7.5=5.0\ text{cm}`

`=>B`

♦ Mean mark 42%.

Financial Maths, STD2 F1 2023 HSC 6 MC

An item was purchased for a price of $880, including 10% GST.

What is the amount of GST included in the price?

$8.00
$8.80
$80.00
$88.00

Show Answers Only

`=>C`

Show Worked Solution

`text{Let}\ C =\ text{Original cost}`

`C+0.1 xx C`	`=880`
`1.1C`	`=880`
`C`	`=880/1.1`
	`=$800`

`:.\ text{GST}\ =800xx0.1=$80`

`=>C`

♦ Mean mark 41%.

BIOLOGY, M2 2013 HSC 35d

Analyse how the use of isotopes has contributed to tracing biochemical pathways in plants. (6 marks)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

Scientists are able to synthesise chemicals with implanted radio-isotopes which organisms use identically to the natural chemicals.
Autoradiography is the use of x-ray or photographic film to detect these radioactive materials. They produce permanent record of positions and relative intensities which scientists can analyse.
$\ce{^3H}$ can be used to track the transport of $\ce{H}$ across the thylakoid membrane.
$\ce{^{32}P}$ can be used to show that water moves in xylem vessels. When roots were surrounded by water containing $\ce{^{32}P}$, it shown it was taken up by the roots, then through the xylem vessels into other plant organs.

Show Worked Solution

Scientists are able to synthesise chemicals with implanted radio-isotopes which organisms use identically to the natural chemicals.
Autoradiography is the use of x-ray or photographic film to detect these radioactive materials. They produce permanent record of positions and relative intensities which scientists can analyse.
$\ce{^3H}$ can be used to track the transport of $\ce{H}$ across the thylakoid membrane.
$\ce{^{32}P}$ can be used to show that water moves in xylem vessels. When roots were surrounded by water containing $\ce{^{32}P}$, it shown it was taken up by the roots, then through the xylem vessels into other plant organs.

BIOLOGY, M2 2014 HSC 14 MC

The current theory to explain the movement of materials within the phloem of a living plant involves the following steps:

1. Osmosis
2. Active transport of sugars into non-photosynthetic cells
3. Active transport of sugars from photosynthetic cells
4. Flow of sugar solution up and down

Which of the following is the correct order of these steps?

3, 4, 1, 2
2, 4, 1, 3
1, 3, 2, 4
3, 1, 4, 2

Show Answers Only

$D$

Show Worked Solution

By Elimination

Sugars are created in photosynthetic cells but are required in all cells. Phloem are the series of cells which allow the transport of sugars in plants, and therefore the steps must start with 3 and end with 2 (Eliminate B and C).
The current theory states that the movement of materials is driven by osmotic pressure, and therefore osmosis must occur before materials are able to move (Eliminate A).

$\Rightarrow D$

♦ Mean mark 43%.

BIOLOGY, M2 2014 HSC 8 MC

What is the most suitable title for this diagram?

A section of xylem tissue
A section of phloem tissue
A transverse section of phloem tissue
A longitudinal section of xylem and phloem tissue

Show Answers Only

$B$

Show Worked Solution

By Elimination

The structure shown is one cell thick, and therefore must be phloem, not xylem (Eliminate A and D).
The section shown is a longitudinal, not transverse, as a transverse section would show only one cell as it would be viewed from the top or bottom (Eliminate C).

$\Rightarrow B$

♦ Mean mark 39%.

BIOLOGY, M3 2015 HSC 30

The graph shows the history of the relative numbers of three varieties of bird $(X, Y$ and $Z$ ) within a bird species, on a remote island in the Pacific Ocean.

The bird species arrived on the island in a migration event. Before migration, the bird species was not present on the island.

The graph record of bird numbers on the island is divided into two sections (1 and 2). Over the time data were recorded, the environment of the island did not change.

What bird varieties originally migrated to the island? (1 mark)

--- 1 WORK AREA LINES (style=lined) ---
Using the Darwin/Wallace theory of evolution, and making reference(s) to the data in the graph, explain the changes to the population of each variety of bird in
i. section (1) of the graph. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
ii. section (2) of the graph. (4 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

a. Varieties $Z$ and $Y$.

b.i. In section (1):

Variety $Z$ is naturally selected as its numbers grow over time until they plateau when it reaches the limits of resources the environment can provide.
Variety $Y$ is not naturally selected as it is not suited to the environment and becomes extinct as its numbers fall over time to zero.

b.ii. In section (2):

Variety $X$ develops, likely from mutation.
Variety $Z$ faces competition from variety $X$ as the numbers of variety $Z$ quickly fall as the numbers of variety $X$ quickly grow. This shows that variety $X$ possesses characteristics which vary from $Z$ and make it more suited to the island.
Variety $Z$ population remains at low levels due to the difficulty of competing for resources with variety $X$, yet they do not go extinct but instead become a minority variety in the species.
The numbers of variety $X$ plateau off at a lower level than variety $Z$ as it reaches the limits of resources the environment can provide for both variety $Z$ and $X$.

Show Worked Solution

a. Varieties $Z$ and $Y$.

b.i. In section (1):

Variety $Z$ is naturally selected as its numbers grow over time until they plateau when it reaches the limits of resources the environment can provide.
Variety $Y$ is not naturally selected as it is not suited to the environment and becomes extinct as its numbers fall over time to zero.

♦ Mean mark (b)(i) 47%.

b.ii. In section (2):

Variety $X$ develops, likely from mutation.
Variety $Z$ faces competition from variety $X$ as the numbers of variety $Z$ quickly fall as the numbers of variety $X$ quickly grow. This shows that variety $X$ possesses characteristics which vary from $Z$ and make it more suited to the island.
Variety $Z$ population remains at low levels due to the difficulty of competing for resources with variety $X$, yet they do not go extinct but instead become a minority variety in the species.
The numbers of variety $X$ plateau off at a lower level than variety $Z$ as it reaches the limits of resources the environment can provide for both variety $Z$ and $X$.

♦ Mean mark (b)(ii) 47%.

BIOLOGY, M2 2015 HSC 36e

'Science has been used to solve problems in the investigation of photosynthesis, and so has provided information of benefit to society.'

Justify this statement with reference to the scientific knowledge behind radioactive tracers for the study of photosynthesis. (7 marks)

--- 20 WORK AREA LINES (style=lined) ---

Show Answers Only

The intricate nature of photosynthesis has posed many barriers when scientists attempt to study it. To overcome this scientists have used radioactive tracers, synthetic chemicals which are taken up by the plant and act as normal organic chemicals except they contain a radioactive component.
Radioactive atoms release radiation that can be seen by technologies like X-ray film, geiger counters etc. The pathway of a radioactive substance through the living thing can be followed, as can the biochemical pathways that the molecule/atom is involved in.
$\ce{C^{14}O2}$ and $\ce{H2O^{18}}$ are both radioactive tracers that can be used to study photosynthesis.
If plants are surrounded by $\ce{C^{14}O2 (g)}$ the radioactivity is soon seen in starch granules in the leaves of the plant. This shows that the starch is formed from the $\ce{CO2}$ in the air, and is composed of carbon atoms from the air. None of the $\ce{C^{14}}$ in the $\ce{C^{14}O2 (g)}$ taken in by the plant is lost.
If plants are watered with $\ce{H2O^{18} (l)}$ the radioactivity is seen in the $\ce{O2}$ that the plant releases into the air around the plant and not in molecules constructed by photosynthesis contained within the leaf.
Therefore in photosynthesis the water is split and the oxygen released into the atmosphere, the $\ce{H}$ incorporated into the plant within intermediate molecules in a biochemical pathway, and then finally into a starch molecule.
This knowledge is of benefit to society because we need to find ways of reducing the carbon in the atmosphere because of excess use of fossil fuel combustion and its resultant climate change. We can understand that land clearing with its removal of photosynthetic species will exacerbate the build up of carbon in the atmosphere because of the loss of photosynthesis it causes.
Society is also concerned about the need to generate oxygen such as in the context of massive amounts of fossil fuel combustion also removing oxygen from the atmosphere. Understanding that plants release oxygen in photosynthesis is part of the offsets for fossil fuel use in re-forestation projects as the carbon is locked up in the plant and oxygen is released into the atmosphere.

Show Worked Solution

The intricate nature of photosynthesis has posed many barriers when scientists attempt to study it. To overcome this scientists have used radioactive tracers, synthetic chemicals which are taken up by the plant and act as normal organic chemicals except they contain a radioactive component.
Radioactive atoms release radiation that can be seen by technologies like X-ray film, geiger counters etc. The pathway of a radioactive substance through the living thing can be followed, as can the biochemical pathways that the molecule/atom is involved in.
$\ce{C^{14}O2}$ and $\ce{H2O^{18}}$ are both radioactive tracers that can be used to study photosynthesis.
If plants are surrounded by $\ce{C^{14}O2 (g)}$ the radioactivity is soon seen in starch granules in the leaves of the plant. This shows that the starch is formed from the $\ce{CO2}$ in the air, and is composed of carbon atoms from the air. None of the $\ce{C^{14}}$ in the $\ce{C^{14}O2 (g)}$ taken in by the plant is lost.
If plants are watered with $\ce{H2O^{18} (l)}$ the radioactivity is seen in the $\ce{O2}$ that the plant releases into the air around the plant and not in molecules constructed by photosynthesis contained within the leaf.
Therefore in photosynthesis the water is split and the oxygen released into the atmosphere, the $\ce{H}$ incorporated into the plant within intermediate molecules in a biochemical pathway, and then finally into a starch molecule.
This knowledge is of benefit to society because we need to find ways of reducing the carbon in the atmosphere because of excess use of fossil fuel combustion and its resultant climate change. We can understand that land clearing with its removal of photosynthetic species will exacerbate the build up of carbon in the atmosphere because of the loss of photosynthesis it causes.
Society is also concerned about the need to generate oxygen such as in the context of massive amounts of fossil fuel combustion also removing oxygen from the atmosphere. Understanding that plants release oxygen in photosynthesis is part of the offsets for fossil fuel use in re-forestation projects as the carbon is locked up in the plant and oxygen is released into the atmosphere.

BIOLOGY, M2 2016 HSC 36e

'Over the past 400 years, the development of our knowledge of the chemical transformations occurring both inside and outside plants has led to our current understanding of photosynthesis.'

Evaluate this statement with reference to the experiments of TWO named scientists. (7 marks)

--- 16 WORK AREA LINES (style=lined) ---

Show Answers Only

In 1774 Joseph Priestley made observations about changes to the air around a living plant. He observed a candle would burn longer within a bell jar of air if a plant were included under the bell jar.
He deduced that the burning of the candle was using up something in the air and thus had a limited burning time in a fixed volume of air. He further deduced the plant was reversing that change and restoring the air to allow the candle to burn longer.
Priestley later described a gas (oxygen) used up from air in combustion of the candle, yet released by plants. Adding oxygen to the outside air mixture can be termed a chemical transformation of air done by plants. This led to the understanding that photosynthesis produces oxygen.

Data collected inside the plant

The experiments by Calvin in the 1940s involved an illuminated flattened glass vessel, wide but thin, containing microscopic algae in solution. The algae were given a pulse of radioactive carbon dioxide $\ce{(^{14}CO2)}$, injected into a stream of air into the vessel.
Samples of Chlorella were then released at intervals (3, 5, 10 seconds and then 15 second periods) into boiling alcohol to kill the algae and stop the progress of biochemical reactions containing the $\ce{(^{14}CO2)}$.
Compounds that the radioactive carbon had reached at a particular moment were determined by two-dimensional paper chromatography and autoradiography after the chlorella cells were broken up.
New chemicals formed were deduced with the same results with chromatography of standard chemicals. For example, phosphoglycerate was identified as the first metabolite in the carbon cycle that was then changed into the glyceraldehyde phosphate.
In this way the series of chemical transformations of carbon compounds in the light-independent reactions of photosynthesis could be followed.
The work of scientists studying both the external and internal environments was essential in developing our understanding of photosynthesis.

Show Worked Solution

In 1774 Joseph Priestley made observations about changes to the air around a living plant. He observed a candle would burn longer within a bell jar of air if a plant were included under the bell jar.
He deduced that the burning of the candle was using up something in the air and thus had a limited burning time in a fixed volume of air. He further deduced the plant was reversing that change and restoring the air to allow the candle to burn longer.
Priestley later described a gas (oxygen) used up from air in combustion of the candle, yet released by plants. Adding oxygen to the outside air mixture can be termed a chemical transformation of air done by plants. This led to the understanding that photosynthesis produces oxygen.

Data collected inside the plant

The experiments by Calvin in the 1940s involved an illuminated flattened glass vessel, wide but thin, containing microscopic algae in solution. The algae were given a pulse of radioactive carbon dioxide $\ce{(^{14}CO2)}$, injected into a stream of air into the vessel.
Samples of Chlorella were then released at intervals (3, 5, 10 seconds and then 15 second periods) into boiling alcohol to kill the algae and stop the progress of biochemical reactions containing the $\ce{(^{14}CO2)}$.
Compounds that the radioactive carbon had reached at a particular moment were determined by two-dimensional paper chromatography and autoradiography after the chlorella cells were broken up.
New chemicals formed were deduced with the same results with chromatography of standard chemicals. For example, phosphoglycerate was identified as the first metabolite in the carbon cycle that was then changed into the glyceraldehyde phosphate.
In this way the series of chemical transformations of carbon compounds in the light-independent reactions of photosynthesis could be followed.
The work of scientists studying both the external and internal environments was essential in developing our understanding of photosynthesis.

BIOLOGY, M2 2016 HSC 17 MC

Capillaries have thin walls that help them perform their main function.

The best explanation for this is that

capillaries are the smallest vessels in the body.
thin walls are an adaptation that help diffusion.
blood flow in capillaries is under very low pressure.
thin walls maximise the surface area available for gas exchange.

Show Answers Only

$\Rightarrow B$

Show Worked Solution

Thin walls are needed in capillaries as this helps oxygen and carbon dioxide be diffused in and out much easier.

$\Rightarrow B$

♦ Mean mark 47%.

BIOLOGY, M2 2016 HSC 16 MC

Ringbarking is the removal of a thin strip of bark from the entire circumference of a tree.

The tree will initially survive, but the roots will eventually die because ringbarking stops

photosynthesis.
the transport of water.
the transport of oxygen.
the transport of dissolved nutrients.

Show Answers Only

$D$

Show Worked Solution

Ringbarking removes a large portion, or even all, of the living part of the tree. This will eventually kill the roots as the transport of sugar from the leaves to the roots will be disrupted or ceased completely.

$\Rightarrow D$

♦ Mean mark 49%.

BIOLOGY, M1 2016 HSC 9 MC

Why is passive transport alone inadequate for the production of urine that is high in nitrogenous wastes?

Osmosis cannot target specific solutes.
Solutes cannot move against a concentration gradient.
Solute transport increases at low concentration gradients.
Osmosis moves water from a low concentration to a high concentration.

Show Answers Only

$B$

Show Worked Solution

Highly concentrated urine must move against the concentration gradient to be able to be excreted from the body.

$\Rightarrow B$

♦ Mean mark 53%.

BIOLOGY, M1 2017 HSC 36e

Analyse the impact of the development of the electron microscope on the understanding of chloroplast structure and function. (7 marks)

--- 14 WORK AREA LINES (style=lined) ---

Show Answers Only

Using light microscopes, scientists were able to view and identify chloroplasts. However, it wasn’t until the development of the electron microscope with its greater magnification and resolution, that scientists were able to view a chloroplast’s internal structure.
Structures such as the grana, stroma and thylakoids could then be identified. The role of each in the process of photosynthesis could then be studied.
Thylakoids are flattened, hollow discs which are arranged in stacks called grana. The stacking of the layers into grana increases stability and surface area for the capture of light.
The membranes of these thylakoids contain chlorophyll and are the site for the light-dependent reactions of photosynthesis.
The space outside the thylakoid is called the stroma, which is an aqueous fluid present within the inner membrane of the chloroplast. It contains DNA, ribosomes, lipid droplets and starch granules. This is where the light independent reactions, the Calvin cycle, takes place.
The functions described would not have been linked to the internal structures of the chloroplast without the development of an electron microscope.

Show Worked Solution

Using light microscopes, scientists were able to view and identify chloroplasts. However, it wasn’t until the development of the electron microscope with its greater magnification and resolution, that scientists were able to view a chloroplast’s internal structure.
Structures such as the grana, stroma and thylakoids could then be identified. The role of each in the process of photosynthesis could then be studied.
Thylakoids are flattened, hollow discs which are arranged in stacks called grana. The stacking of the layers into grana increases stability and surface area for the capture of light.
The membranes of these thylakoids contain chlorophyll and are the site for the light-dependent reactions of photosynthesis.
The space outside the thylakoid is called the stroma, which is an aqueous fluid present within the inner membrane of the chloroplast. It contains DNA, ribosomes, lipid droplets and starch granules. This is where the light independent reactions, the Calvin cycle, takes place.
The functions described would not have been linked to the internal structures of the chloroplast without the development of an electron microscope.

BIOLOGY, M1 2017 HSC 20 MC

A student performed a valid enzyme-substrate experiment. At the end of each 10-minute period, the quantity of the gaseous product formed was collected,

removed and measured. The graph shows the results of this experiment.

Which of the following statements explains the trend shown in the graph?

The rate of enzyme activity is decreasing.
The concentration of the product is decreasing.
The concentration of the enzyme is decreasing.
The concentration of the substrate is decreasing.

Show Answers Only

$D$

Show Worked Solution

The graph shows that over the periods, the substrate concentration/quantity decreased.

$\Rightarrow D$

♦♦ Mean mark 37%.

BIOLOGY, M1 2017 HSC 18 MC

A student used a microscope to estimate the size of blood cells. Two types of cells were observed. The student estimated one type to be about 50% larger than the other.

Which of the following could be used to assess the accuracy of the student's findings?

The size of other body cells
The sizes of blood cells estimated by other students
The expected sizes of blood cells quoted in scientific literature
The average size of blood cells from three repetitions of the investigation

Show Answers Only

$C$

Show Worked Solution

By Elimination

Comparing to other body cells would have no relevance to the estimation being addressed (Eliminate A).
Both options B and D would assess the reliability of the findings, not the accuracy. (Eliminate B and D).

$\Rightarrow C$

♦ Mean mark 44%.

\(1 \times \ddot{x} \)	\(=-4 \dot{x} \)
\(\dfrac{d\dot{x}}{dt}\)	\(=-4\dot{x}\)
\(\dfrac{dt}{d\dot{x}}\)	\(= -\dfrac{1}{4\dot{x}} \)
\(t\)	\(=-\dfrac{1}{4} \displaystyle \int \dfrac{1}{\dot{x}} \ d\dot{x} \)
\(-4t\)	\(=\ln \|\dot{x}\|+c \)

\(-4t\)	\(=\ln\|\dot{x}\|-\ln 20\sqrt3 \)
\(-4t\)	\(=\ln\Bigg{\|}\dfrac{\dot{x}}{20\sqrt{3}} \Bigg{\|} \)
\(\dfrac{\dot{x}}{20\sqrt{3}} \)	\(=e^{-4t} \)
\(\dot{x}\)	\(=20\sqrt{3}e^{-4t}\)

\(1 \times \ddot{y} \)	\(=-1 \times 10-4 \dot{y} \)
\(\dfrac{d\dot{y}}{dt}\)	\(=-(10+4\dot{y})\)
\(\dfrac{dt}{d\dot{y}}\)	\(= -\dfrac{1}{10+4\dot{y}} \)
\(t\)	\(=- \displaystyle \int \dfrac{1}{10+4\dot{y}} \ d\dot{y} \)
\(-4t\)	\(=- \displaystyle \int \dfrac{4}{10+4\dot{y}} \ d\dot{y} \)
\(-4t\)	\(=\ln \|10+4\dot{y}\|+c \)

\(-4t\)	\(=\ln\|10+4\dot{y}\|-\ln 90 \)
\(-4t\)	\(=\ln\Bigg{\|}\dfrac{10+4\dot{y}}{\ln{90}} \Bigg{\|} \)
\(\dfrac{10+4\dot{y}}{90} \)	\(=e^{-4t} \)
\(4\dot{y}\)	\(=90e^{-4t}-10\)
\(\dot{y}\)	\(=\dfrac{45}{2} e^{-4t}-\dfrac{5}{2} \)

\(x\)	\(= \displaystyle \int \dot{x}\ dx\)
	\(= \displaystyle \int 20\sqrt3 e^{-4t}\ dt \)
	\(=-5\sqrt3 e^{-4t}+c \)

\(x\)	\(=5\sqrt3-5\sqrt3 e^{-4t} \)
	\(=5\sqrt3(1-e^{-4t}) \)

\(y\)	\(=\dfrac{45}{8}-\dfrac{45}{8} e^{-4t}-\dfrac{5}{2}t \)
	\(=\dfrac{45}{8}(1-e^{-4t})-\dfrac{5}{2} \)

\(\dfrac{45}{8}(1-e^{-4t})-\dfrac{5}{2}t \)	\(=0\)
\(\dfrac{45}{8}(1-e^{-4t}) \)	\(=\dfrac{5}{2}t \)
\(1-e^{-4t}\)	\(=\dfrac{4}{9}t \)

\(\therefore\ \text{Range}\)	\(=5\sqrt3(1-e^{(-4 \times 2.25)}) \)
	\(=8.659…\)
	\(=8.7\ \text{metres (to 1 d.p.)}\)