In one year, a factory makes:
- eleven thousand and twenty-five bikes
- three thousand, nine hundred and seven scooters
Write these as numbers in the boxes below:
|
|
bikes |
|
|
scooters |
Aussie Maths & Science Teachers: Save your time with SmarterEd
In one year, a factory makes:
Write these as numbers in the boxes below:
|
|
bikes |
|
|
scooters |
`text(11 025 bikes)`
`text(3907 scooters)`
`text(11 025 bikes)`
`text(3907 scooters)`
Patrick gets $7.35 in pocket money each week.
He does extra jobs one week and earns $4.75 more.
How much money did Patrick receive in total in the week?
| `$11.00` | `$11.10` | `$12.00` | `$12.10` |
|
|
|
|
|
`$12.10`
`$7.35 + 4.75 = $12.10`
The bottles in Renee's fridge are pictured below.
Renee decides to make a graph where each bar represents one type of bottle in her fridge.
Renee makes an error when creating the graph.
What should Renee do to correct the error?
|
|
Make each category bar a different colour. |
|
|
Change the title to 'Number of bottles in the fridge by volume'. |
|
|
Change the 'Number of bottles' label to 'Volume of bottles'. |
|
|
Remove the 'Juice' category since orange juice and apple juice are already shown. |
`text(Remove the ‘Juice’ category since orange juice and)`
`text(apple juice are already shown.)`
`text(Remove the ‘Juice’ category since orange juice and)`
`text(apple juice are already shown.)`
Madison uses the number sentence 15 × 12 = 180 to solve a problem.
Which of the following could be the problem?
|
|
Madison buys 15 showbags. How much does each showbag cost? |
|
|
Madison spends $15 on 180 showbags. How much does she spend? |
|
|
Madison buys 15 showbags that cost $12 each. How many showbags does she buy? |
|
|
Madison buys 12 showbags that cost $15 each. How much does she spend? |
`text(Madison buys 12 showbags that cost $15 each.)`
`text(How much does she spend?)`
`text($15 per showbag × 12 showbags = $180)`
`:.\ text(Madison buys 12 showbags that cost $15 each.)`
`text(How much does she spend?)`
A map of the huts in Ghengis Khan's camp is drawn below.
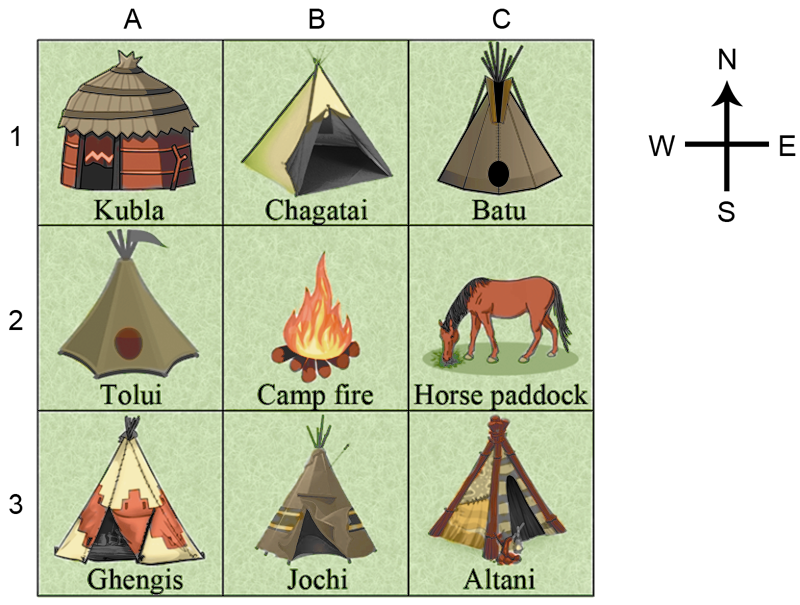
In what direction is Ghengis' hut from Batu's hut?
|
|
north-west |
|
|
north-east |
|
|
north |
|
|
south-west |
|
|
south-east |
|
|
south |
`text(south-west)`
`text(south-west)`
Claudia gets to ring the school bell once every 5 school days.
Today is a school day.
What is the probability that Claudia will ring the school bell?
| `text(5%)` | `0.35` | `1/5` | `5/7` |
|
|
|
|
|
`1/5`
| `P text{(Claudia rings bell)}` | `=text(favorable events)/text(total possible events)` |
| `= 1/5` |
Dinesh is a teacher and buys pencils for his class.
He purchases the pencils in two different sized packets.
Dinesh buys 10 packet A's and 4 packet B's.
He then divides all the pencils equally among his 9 students.
How many pencils does each student receive?
| `6` | `8` | `12` | `54` | `72` |
|
|
|
|
|
|
`8`
| `text(Total pencils)` | `=(10 xx 6)+(4 xx3)` |
| `=72` |
| `:.\ text(Pencils per student)` | `=72 -: 9` |
| `=8` |
Milly purchases 48 batteries.
The batteries come in packets of 8.
Which number sentence shows the number of packets of batteries Milly buys?
| `48 ÷ 8 = 6` | `48 + 8 = 56` | `48 - 8 = 40` | `48 xx 8 = 384` |
|
|
|
|
|
`48 ÷ 8 = 6`
`48 ÷ 8 = 6`
There are 48 Year 7 students at a high school.
Each student is asked if they own a bike or not and the results are recorded.
`3/4` of the students said they owned a bike.
How many Year 7 students at the school own a bike?
`36`
`text(Students who own a bike)`
`= 3/4 xx 48`
`= 36`
A school teacher allocates pieces of cardboard to class groups depending on the number of students in each group.
The table below is used.
Using the pattern in the table, how many pieces of cardboard should a group of 3 students receive?
`9`
`text(The pattern shows that each student receives)`
`text(2 pieces of cardboard.)`
`:.\ text(A group of 3 will be given 9 pieces.)`
Claudia gets to ring the school bell once every 5 school days.
Today is a school day.
What is the probability that Claudia will ring the school bell?
| `text(5%)` | `0.35` | `1/5` | `5/7` |
|
|
|
|
|
`1/5`
| `P` | `=text(favorable events)/text(total possible events)` |
| `= 1/5` |
`{x: cos^2(x) + 2cos (x) = 0} =`
`A`
`text(Factorise:)`
`cos (x) (cos x + 2) = 0`
`:. cos x = 0,\ \ text(or)`
`cos x = -2 -> text(no solution)`
`=> A`
Let `f: [0, pi/2] -> R,\ f(x) = sin(4x) + 1.` The graph of `f` is transformed by a reflection in the `x`-axis followed by a dilation of factor 4 from the `y`-axis.
The resulting graph is defined by
`E`
`f(x) = sin(4x)+1`
`text(Reflecting in the)\ x text(-axis,)`
`=> h(x) = – sin (4x) – 1`
`text(Dilation by a factor of 4 from the)\ \ y text(-axis,)`
`=> g(x) = -sin(x)-1`
`text(Dilation factor: adjust the domain from)\ \ [0, pi/2]`
`text(to)\ \ [0xx4, pi/2 xx 4]=[0,2pi].`
`=> E`
The sample space when a fair die is rolled is `{1, 2, 3, 4, 5, 6}`, with each outcome being equally likely.
For which of the following pairs of events are the events independent?
`E`
| `text(Let)\ \ A` | `= {1, 2}` |
| `B` | `= {2, 4, 6}` |
| `A nn B` | `= {2}` |
| `text(Pr)(A)` | `= 1/3` |
| `text(Pr)(B)` | `= 1/2` |
| `text(Pr)(A nn B)` | `= 1/6` |
| `text(S) text(ince)\ \ text(Pr) (A) xx text(Pr) (B)` | `= text(Pr)(A nn B)` |
| `1/3 xx 1/2` | `= 1/6` |
`:. A, B\ \ text(are independent.)`
`=> E`
The diagram shows the function `f:(2, oo)→R`, where `f(x)= log_e(x - 2).`
In the diagram, the shaded region is bounded by `f(x)`, the `x`-axis and the line `x = 7`.
Find the exact value of the area of the shaded region. (4 marks)
`5log_e 5 – 4\ \ \ text(u²)`
| `text(Shaded Area)\ (A_1)` | `= text(Rectangle) – A_2` |
| `text(Area of Rectangle)` | `= 7 xx log_e 5` |
`text(Finding the Area of)\ A_2`
| `y` | `= log_e(x – 2)` |
| `x – 2` | `= e^y` |
| `x` | `= e^y + 2` |
| `:. A_2` | `= int_0^(log_e5) x\ dy` |
| `= int_0^(log_e5) e^y + 2\ dy` | |
| `= [e^y + 2y]_0^(log_e5)` | |
| `= [(e^(log_e 5) + 2log_e5) – (e^0 + 0)]` | |
| `= (5 + 2log_e 5) – 1` | |
| `= 4 + 2log_e 5` |
| `:. A_1` | `= 7 log_e5 – (4 + 2log_e 5)` |
| `= 5log_e 5 – 4\ \ \ text(u²)` |
Let `X` be a continuous random variable with probability density function `f(x) = {(−4xlog_e(x),0<x<=1),(0,text(elsewhere)):}` Part of the graph of `f` is shown below. The graph has a turning point at `x = 1/e`. --- 5 WORK AREA LINES (style=lined) --- --- 5 WORK AREA LINES (style=lined) ---
a. `text(Using Product Rule:)` `d/(dx) ((x^k)/(k^2)(klog_e(x)-1))` `=d/(dx)((x^k)/k log_e(x)-(x^k)/(k^2))` `= x^(k-1) log_e(x) + 1/k x^(k-1)-1/k x^(k-1)` `= x^(k-1) log_e(x)` `:. intx^(k-1) log_e(x)\ dx = (x^k)/(k^2)(klog_e(x)-1)` b. `text(Pr)(x > 1/e)` `= −4 int_(1/e)^1 (xlog_e(x))\ dx,\ text(where)\ k = 2` `= −4[(x^2)/4(2log_e(x)-1)]_(1/e)^1` `= −4[1/4(0 -1)-1/(4e^2)(2log_e(e^(−1))-1)]` `= −4[−1/4 + 1/(4e^2) + 1/(2e^2)]` `= 1-3/(e^2)`
MARKER’S COMMENT: Students who expanded before differentiating tended to score more highly.
The sample space when a fair twelve-sided die is rolled is `{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}`. Each outcome is equally likely.
For which one of the following pairs of events are the events independent?
`A`
`text(Consider option A:)`
`text(Let)\ \A = {1, 3, 5, 7, 9, 11}`
`text(Let)\ \ B = {1, 4, 7, 10}`
`A nn B = {1, 7}`
`text(If independent events,)`
`text(Pr) (A nn B) = text(Pr) (A) xx text(Pr) (B)`
`text(Pr) (A) = 6/12=1/2`
`text(Pr) (B) = 4/12=1/3`
`text(Pr) (A nn B) = 2/12=1/6`
`:.\ text(Pr) (A nn B) = text(Pr) (A) xx text(Pr) (B)`
`:. A, B\ \ text(are independent)`
`=> A`
Deep in the South American jungle, Tasmania Jones has been working to help the Quetzacotl tribe to get drinking water from the very salty water of the Parabolic River. The river follows the curve with equation `y = x^2-1`, `x >= 0` as shown below. All lengths are measured in kilometres.
Tasmania has his camp site at `(0, 0)` and the Quetzacotl tribe’s village is at `(0, 1)`. Tasmania builds a desalination plant, which is connected to the village by a straight pipeline.
--- 6 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
The desalination plant is actually built at `(sqrt7/2, 3/4)`.
If the desalination plant stops working, Tasmania needs to get to the plant in the minimum time.
Tasmania runs in a straight line from his camp to a point `(x,y)` on the river bank where `x <= sqrt7/2`. He then swims up the river to the desalination plant.
Tasmania runs from his camp to the river at 2 km per hour. The time that he takes to swim to the desalination plant is proportional to the difference between the `y`-coordinates of the desalination plant and the point where he enters the river.
`qquadT = 1/2 sqrt(x^4-x^2 + 1) + 1/4k(7-4x^2)` hours where `k` is a positive constant of proportionality. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
The value of `k` varies from day to day depending on the weather conditions.
--- 1 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
a. `text(S)text(ince)\ \ (m,n)\ \ text(lies on)\ \ y=x^2-1,`
`=> n=m^2-1`
`V(0,1), D(m,m^2-1)`
| `L` | `= sqrt((m-0)^2 + ((m^2-1)-1)^2)` |
| `= sqrt(m^2 + m^4-4m^2 + 4)` | |
| `= sqrt(m^4-3m^2 + 4)\ \ text(… as required)` |
b.i. `(dL)/(dm) = (2m^2-3m)/(sqrt(m^4-3m^2 + 4))`
`text(Solve:)\ \ (dL)/(dm) = 0quadtext(for)quadm >= 0`
`\Rightarrow m = sqrt6/2`
`text(Substitute into:)\ \ D(m, m^2-1),`
`:. text(Desalination plant at)\ \ (sqrt6/2, 1/2)`
| b.ii. | `L(sqrt6/2)` | `= sqrt(m^4-3m^2 + 4)` |
| `=sqrt(36/16-3xx6/4+4` | ||
| `=sqrt7/2` |
c. `text(Let)\ \ P(x,x^2-1)\ text(be run point on bank)`
`text(Let)\ \ D(sqrt7/2, 3/4)\ text(be desalination location)`
| `T` | `=\ text(run time + swim time)` |
| `= (sqrt((x-0)^2 + ((x^2-1)-0)^2))/2 + k(3/4-(x^2-1))` | |
| `= (sqrt(x^2 + x^4-2x^2 + 1))/2 + k/4(3-4(x^2-1))` | |
| `:. T` | `= (sqrt(x^4-x^2 + 1))/2 + 1/4k(7-4x^2)` |
d.i. `(dT)/(dx) = (x(2x^2-1))/(2sqrt(x^4-x^2 + 1))-(sqrt13 x)/13`
d.ii. `text(Solve:)\ \ (dT)/(dx) = 0`
`x = sqrt3/2`
`y=x^2-1=-1/4`
`:. T_(text(min)) \ text(when point is)\ \ (sqrt3/2, −1/4)`
e. `(dT)/(dx) = (x(2x^2-1))/(2sqrt(x^4-x^2 + 1))-2kx`
`text(When)\ \ x=1:`
| `text(Solve:)\ \ (dT)/(dx)` | `=0\ \ text(for)\ k,` |
| `1/2 -2k` | `=0` |
| `:.k` | `=1/4` |
f. `text(Require)\ T_text(min)\ text(to occur at right-hand endpoint)\ \ x = sqrt7/2.`
`text(This can occur in 2 situations:)`
`text(Firstly,)\ \ T\ text(has a local min at)\ \ x = sqrt7/2,`
`text(Solve:)\ \ (x(2x^2-1))/(2sqrt(x^4-x^2 + 1))-2kx=0| x = sqrt7/2,\ \ text(for)\ k,`
`:.k = (5sqrt37)/74`
`text(S)text(econdly,)\ \ T\ text(is decreasing function over)\ x ∈ (0, sqrt7/2),`
`text(Solve:)\ \ (dT)/(dx) <= 0 | x = sqrt7/2,\ text(for)\ k,`
`:. k > (5sqrt37)/74`
`:. k >= (5sqrt37)/74`
--- 1 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 8 WORK AREA LINES (style=lined) ---
a.i. `f^{prime}(x) = 12x^2 + 5`
a.ii. `text(S)text(ince)\ \ x^2>=0\ \ text(for all)\ x,`
| ` 12x^2` | `>= 0` |
| `12x^2 + 5` | `>= 5` |
| `f^{prime}(x)` | `>= 5\ \ text(for all)\ x` |
b.i. `p(x) = text(is a cubic)`
`:. m = 0, 1, 2`
`text{(Note: part a.ii shows that a cubic may have no SP’s.)}`
b.ii. `text(For)\ p^(−1)(x)\ text(to exist)`
`:. m = 0, 1`
c.i. `text(Let)\ y = q(x)`
`text(Inverse: swap)\ x ↔ y`
| `x` | `= 3-2y^3` |
| `y^3` | `= (3-x)/2` |
`:. q^(-1)(x) = root(3)((3-x)/2), \ x ∈ R`
c.ii. `text(Any function and its inverse intersect on)`
`text(the line)\ \ y=x.`
| `text(Solve:)\ \ 3-2x^3` | `= xqquadtext(for)\ x,` |
| `x` | `= 1` |
`:.\ text{Intersection at (1, 1)}`
| d.i. | `g^{prime}(x)` | `= 0` |
| `3x^2 + 4x + c` | `= 0` | |
| `Delta` | `= 0` | |
| `16-4(3c)` | `= 0` | |
| `:. c` | `= 4/3` |
d.ii. `text(Define)\ \ g(x) = x^3 + 2x^2 + 4/3x + k`
`text(Stationary point when)\ \ g^{prime}(x)=0`
`g^{prime}(x) = 3x^2+4x+4/3`
`text(Solve:)\ \ g^{prime}(x)=0\ \ text(for)\ x,`
`x = -2/3`
`text(Intersection of)\ g(x)\ text(and)\ g^(-1)(x)\ text(occurs on)\ \ y = x`
`text(Point of intersection is)\ (-2/3, -2/3)`
`text(Find)\ k:`
| `g(-2/3)` | `= -2/3\ text(for)\ k` |
| `:. k` | ` = -10/27` |
In a chocolate factory the material for making each chocolate is sent to one of two machines, machine A or machine B. The time, `X` seconds, taken to produce a chocolate by machine A, is normally distributed with mean 3 and standard deviation 0.8. The time, `Y` seconds, taken to produce a chocolate by machine B, has the following probability density function `f(y) = {{:(0,y < 0),(y/16,0 <= y <= 4),(0.25e^(−0.5(y-4)),y > 4):}` --- 3 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- --- 5 WORK AREA LINES (style=lined) --- --- 5 WORK AREA LINES (style=lined) --- All of the chocolates produced by machine A and machine B are stored in a large bin. There is an equal number of chocolates from each machine in the bin. It is found that if a chocolate, produced by either machine, takes longer than 3 seconds to produce then it can easily be identified by its darker colour. --- 6 WORK AREA LINES (style=lined) ---
a.i. `0.4938` a.ii. `0.4155` b. `4.333` c. `0.1812` d. `0.4103`
a.i. `X ∼\ N(3,0.8^2)` `text(Pr)(3 <= X <= 5) = 0.4938\ \ text{(4 d.p.)}` c. `text(Solution 1)` `text(Let)\ \ W = #\ text(chocolates from)\ B\ text(that take less)` `text(than 3 seconds)` `W ∼\ text(Bi)(10, 9/32)` `text(Using CAS: binomPdf)(10, 9/32,4)` `text(Pr)(W = 4) = 0.1812\ \ text{(4 d.p.)}` `text(Solution 2)`
a.ii.
`text(Pr)(3 <= Y <= 5)`
`= text(Pr)(3 <= Y <= 4) + (4 < Y <= 5)`
`= int_3^4 (y/16)dy + int_4^5(1/4 e^(−1/2(y-4)))dy`
`= 0.4155\ \ text{(4 d.p.)}`
b.
`text(E)(Y)`
`= int_0^4 y(y/16)dy + int_4^∞ 0.25ye^(−1/2(y-4))dy`
`= 4.333\ \ text{(3 d.p.)}`
`text(Pr)(W = 4)`
`=((10),(4)) (9/32)^4 (23/32)^6`
`=0.1812`
MARKER’S COMMENT: Students who used tree diagrams were the most successful.
d.

`text(Pr)(A | L)`
`= (text(Pr)(AL))/(text(Pr)(L))`
`= (0.5 xx 0.5)/(0.5 xx 0.5 + 0.5 xx 23/32)`
`= 0.4103\ \ text{(4 d.p.)}`
--- 2 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
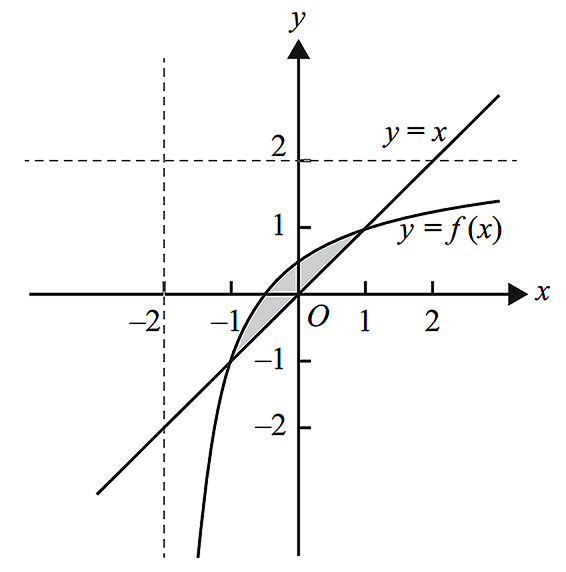
--- 5 WORK AREA LINES (style=lined) ---
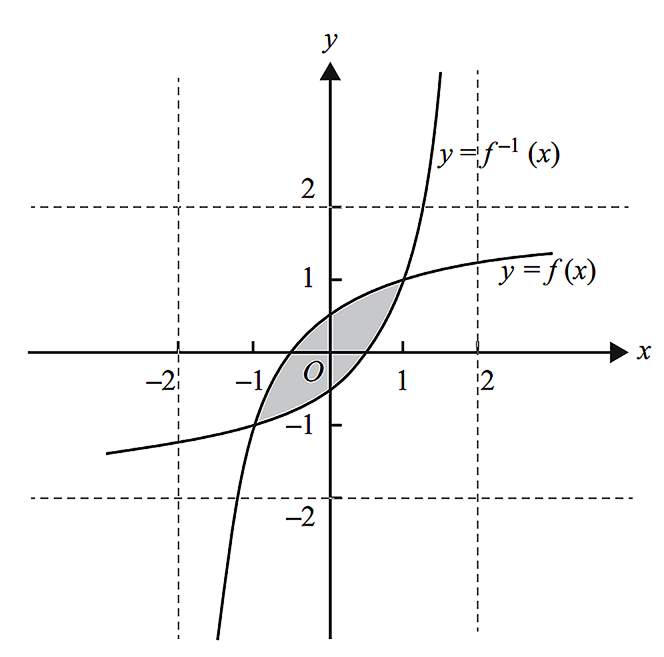
--- 5 WORK AREA LINES (style=lined) ---
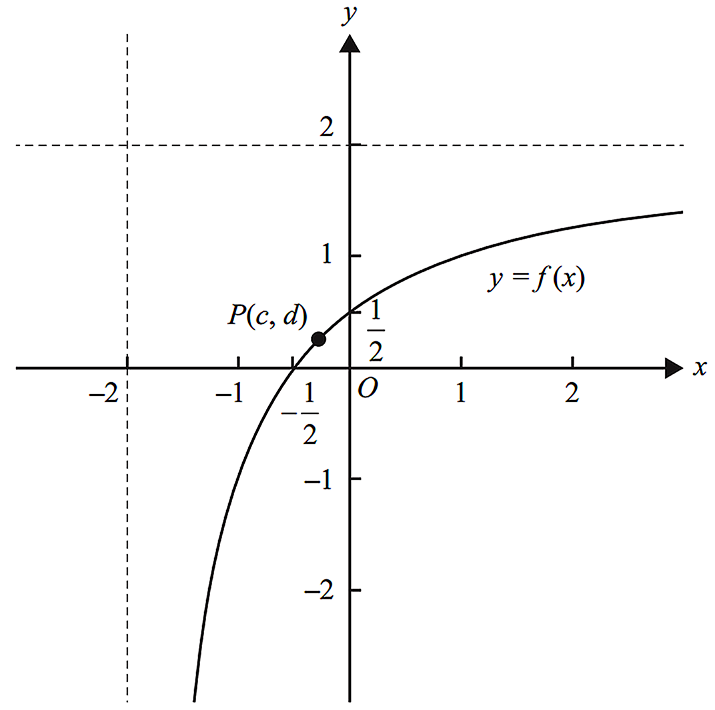
The point `P(c, d)` is on the graph of `f`.
Find the exact values of `c` and `d` such that the distance of this point to the origin is a minimum, and find this minimum distance. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Let `g: (−k, oo) -> R, g(x) = (kx + 1)/(x + k)`, where `k > 1`.
--- 7 WORK AREA LINES (style=lined) ---
--- 7 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
Find the values of `k` such that `s(k) >= 1`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
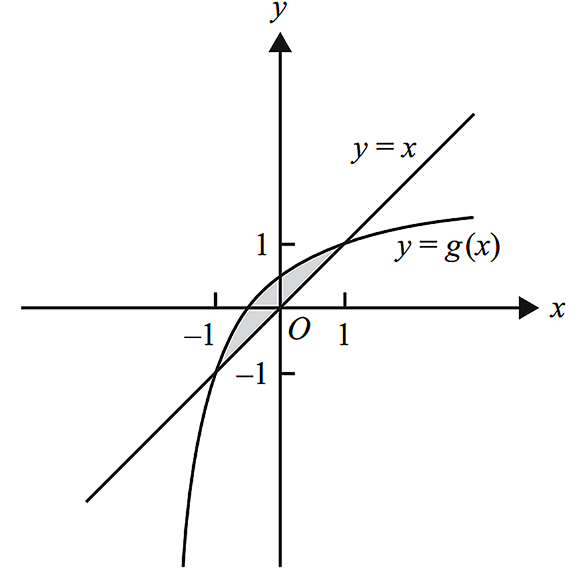
Let `A(k)` be the rule of the function `A` that gives the area of this enclosed region. The domain of `A` is `(1, oo)`.
--- 4 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
a. `text(Solution 1)`
| `(2x + 1)/(x + 2)` | `= 2-3/(x + 2)` |
| `= 2 + {(-3)}/(x + 2) qquad [text(CAS: prop Frac) ((2x + 1)/(x + 2))]` |
`text(Solution 2)`
| `(2x + 1)/(x + 2)` | `=(2(x+2)-3)/(x+2)` |
| `=2+ (-3)/(x+2)` |
b.i. `text(Let)\ \ y = f(x)`
`text(For Inverse: swap)\ \ x ↔ y`
| `x` | `=2-3/(y + 2)` |
| `(x-2)(y+2)` | `=-3` |
| `y` | `=(-3)/(x-2)-2` |
`text(Range of)\ f(x):\ \ y in R text(\){2}`
`:. f^(-1) (x) = (-3)/(x-2)-2, \ x in R text(\){2}`
b.ii. `text(Find intersection points:)`
| `f(x)` | `= x` |
| `(2x+1)/(x+2)` | `=x` |
| `2x+1` | `=x^2+2x` |
| `:. x` | `= +- 1` |
| `:.\ text(Area)` | `= int_(-1)^1 (f(x)-x)\ dx` |
| `=int_(-1)^1 (2-3/(x + 2)-x)\ dx` | |
| `= 4-3 ln(3)\ text(u²)` |
| b.iii. | `text(Area)` | `= int_(-1)^1 (f(x)-f^(-1) (x)) dx` |
| `=2 xx (4-3 ln(3))\ \ \ text{(twice the area in (b)(ii))}` | ||
| `= 8-6 log_e (3)\ text(u²)` |
| c. |  |
|
| `text(Let)\ \ z` | `= OP, qquad P(c, -3/(c + 2) + 2)` | |
| `z` | `= sqrt (c^2 + (2-3/(c + 2))^2), \ c > -2` | |
`text(Stationary point when:)`
`(dz)/(dc) = 0, c > -2`
`:.\ c = sqrt 3-2 overset and (->) d = 2-sqrt 3`
`:. text(Minimum distance) = (2 sqrt 2-sqrt 6)`
d. `text(Given:)\ \ -k < x_1 < x_2`
`text(Must prove:)\ \ g(x_2)-g(x_1) > 0`
`text(LHS:)`
`g(x_2)-g(x_1)`
`= (kx_2 +1)/(x_2+k)-(kx_1 +1)/(x_1+k)`
`=((kx_2 +1)(x_1+k)-(kx_1 +1)(x_2+k))/((x_2+k)(x_1+k))`
`=(k^2(x_2-x_1)-(x_2-x_1))/((x_2+k)(x_1+k))`
`=((k^2-1)(x_2-x_1))/((x_2+k)(x_1+k))`
`x_2-x_1 >0,\ and \ k^2-1>0`
`text(S)text(ince)\ \ x_2>x_1> -k,`
`=> -x_2<-x_1<k`
`=>k+x_1 >0, \ and \ k+x_2>0`
`:.g(x_2)-g(x_1) >0`
`:. g(x_2) > g(x_1)`
| e.i. | `g(x)` | `= -x` |
| `(kx +1)/(x+k)` | `=-x` | |
| `kx+1` | `=-x^2-xk` | |
| `x^2+2k+1` | `=0` | |
| `:. x` | `=(-2k +- sqrt(4k^2-4))/2` | |
| `= sqrt (k^2-1)-k\ \ text(for)\ \ x > -k` |
`:. X (-k + sqrt(k^2-1),\ \ k-sqrt(k^2-1))`
e.ii. `text(Equate)\ \ x text(-coordinates:)`
| `-k + sqrt(k^2-1)` | `= -1/2` |
| `sqrt(k^2-1)` | `=k-1/2` |
| `k^2-1` | `=k^2-k+1/4` |
| `:. k` | `= 5/4` |
| e.iii. | `s(k)` | `= (1/2 xx YZ xx XO)^2` |
| `= 1/4 xx (YZ)^2 xx (XO)^2` |
`ZO = sqrt(1^2+1^2) = sqrt2`
`YZ=2 xx ZO = 2sqrt2`
`(YZ)^2 = 8`
| `(XO)^2` | `=(-k + sqrt(k^2-1))^2-(k-sqrt (k^2-1))^2` |
| `=2(-k + sqrt(k^2-1))^2` | |
`text(Solve)\ \ s(k) >= 1\ \ text(for)\ \ k >= 1,`
| `1/4 xx 8 xx 2(-k + sqrt(k^2-1))^2` | `>=1` |
| `(-k + sqrt(k^2-1))^2` | `>=1/4` |
| `k-sqrt(k^2-1)` | `>=1/2` |
| `k-1/2` | `>= sqrt(k^2-1)` |
| `k^2-k+1/4` | `>=k^2-1` |
| `:.k` | `<= 5/4` |
`:. 1<k<= 5/4`
| f.i. | `A(k)` | `= int_(-1)^1 (g(x)-x)\ dx,\ \ k > 1` |
| `= int_(-1)^1 ((kx+1)/(x+k) -x)\ dx` | ||
| `= int_(-1)^1 (k+ (1-k^2)/(x+k) -x)` | ||
| `=[kx + (1-k^2) log_e(x+k)-x^2/2]_(-1)^1` | ||
| `=(k+(1-k^2)log_e(1+k)-1/2)-(-k+(1-k^2)log_e(k-1)-1/2)` | ||
| `=2k+(1-k^2)log_e ((1+k)/(k-1))` | ||
| `= (k^2-1) log_e ((k-1)/(k + 1)) + 2k` |
| f.ii. |  |
|
| `0` | `< A(k) < text(Area of)\ Delta ABC` | |
| `0` | `< A(k) < 1/2 xx AC xx BO` | |
| `0` | `< A(k) < 1/2 sqrt(2^2 + 2^2) xx (sqrt(1^2 + 1^2))` | |
| `0` | `< A(k) < 1/2 xx 2 sqrt 2 xx sqrt 2` | |
| `:. 0` | `< A(k) < 2` | |
A school has a class set of 22 new laptops kept in a recharging trolley. Provided each laptop is correctly plugged into the trolley after use, its battery recharges. On a particular day, a class of 22 students uses the laptops. All laptop batteries are fully charged at the start of the lesson. Each student uses and returns exactly one laptop. The probability that a student does not correctly plug their laptop into the trolley at the end of the lesson is 10%. The correctness of any student’s plugging-in is independent of any other student’s correctness. --- 5 WORK AREA LINES (style=lined) --- --- 5 WORK AREA LINES (style=lined) --- The time for which a laptop will work without recharging (the battery life) is normally distributed, with a mean of three hours and 10 minutes and standard deviation of six minutes. Suppose that the laptops remain out of the recharging trolley for three hours. --- 5 WORK AREA LINES (style=lined) --- A supplier of laptops decides to take a sample of 100 new laptops from a number of different schools. For samples of size 100 from the population of laptops with a mean battery life of three hours and 10 minutes and standard deviation of six minutes, `hat P` is the random variable of the distribution of sample proportions of laptops with a battery life of less than three hours. --- 6 WORK AREA LINES (style=lined) --- It is known that when laptops have been used regularly in a school for six months, their battery life is still normally distributed but the mean battery life drops to three hours. It is also known that only 12% of such laptops work for more than three hours and 10 minutes. --- 5 WORK AREA LINES (style=lined) --- The laptop supplier collects a sample of 100 laptops that have been used for six months from a number of different schools and tests their battery life. The laptop supplier wishes to estimate the proportion of such laptops with a battery life of less than three hours. --- 2 WORK AREA LINES (style=lined) --- The laptop supplier finds that, in a particular sample of 100 laptops, six of them have a battery life of less than three hours. --- 2 WORK AREA LINES (style=lined) --- `qquad qquad f(x) = {(((210-x)e^((x-210)/20))/400, 0 <= x <= 210), (0, text{elsewhere}):}` --- 2 WORK AREA LINES (style=lined) ---
a. `text(Solution 1)` `text(Let)\ \ X = text(number not correctly plugged),` `X ~ text(Bi) (22, .1)` `text(Pr) (X >= 1) = 0.9015\ \ [text(CAS: binomCdf)\ (22, .1, 1, 22)]` `text(Solution 2)` b. `text(Pr) (X < 5 | X >= 1)` `= (text{Pr} (1 <= X <= 4))/(text{Pr} (X >= 1))` `= (0.83938…)/(0.9015…)\ \ [text(CAS: binomCdf)\ (22, .1, 1,4)]` `= 0.9311\ \ text{(4 d.p.)}` c. `text(Let)\ \ Y = text(battery life in minutes)` `Y ~ N (190, 6^2)` `text(Pr) (Y <= 180)= 0.0478\ \ text{(4 d.p.)}` `[text(CAS: normCdf)\ (−oo, 180, 190,6)]` d. `text(Let)\ \ W = text(number with battery life less than 3 hours)` `W ~ Bi (100, .04779…)` e. `text(Let)\ \ B = text(battery life), B ~ N (180, sigma^2)` g. `text(95% confidence int:) qquad quad [(text(CAS:) qquad qquad 1-text(Prop)\ \ z\ \ text(Interval)), (x = 6), (n = 100)]` `p in (0.01, 0.11)`
`text(Pr) (X>=1)`
`=1-text(Pr) (X=0)`
`=1-0.9^22`
`=0.9015\ \ text{(4 d.p.)}`
`text(Pr) (hat P >= .06 | hat P >= .05)`
`= text(Pr) (X_2 >= 6 | X_2 >= 5)`
`= (text{Pr} (X_2 >= 6))/(text{Pr} (X_2 >= 5))`
`= (0.3443…)/(0.5234…)`
`= 0.658\ \ text{(3 d.p.)}`
`text(Pr) (B > 190)`
`= .12`
`text(Pr) (Z < a)`
`= 0.88`
`a`
`dot = 1.17499…\ \ [text(CAS: invNorm)\ (0.88, 0, 1)]`
`-> 1.17499`
`= (190-180)/sigma\ \ [text(Using)\ Z = (X-u)/sigma]`
`:. sigma`
`dot = 8.5107`
f.
`text(Pr) (MML)`
`= 1/2 xx 1/2 xx 1/2`
`= 1/8`
h.
`mu`
`= int_0^210 (x* f(x)) dx`
`:. mu`
`dot = 170.01\ text(min)`
Let `f` be a differentiable function defined for `x > 2` such that
`int_3^(ab + 2) f (x)\ dx = int_3^(a + 2) f(x)\ dx + int_3^(b + 2) f(x)\ dx` where `a > 1 and b > 1.`
The rule for `f (x)` is
`E`
`text(Solution 1)`
`text(Consider option)\ E:`
| `int_3^(ab + 2) (1/(x-2))\ dx` | `= int_3^(a + 2) (1/(x-2))\ dx + int_3^(b + 2) (1/(x-2))\ dx` |
| `[log_e (x-2)]_3^(ab+2)` | `=[log_e (x-2)]_3^(a+2) + [log_e (x-2)]_3^(b+2)` |
| `log_e(ab)-log_e1` | `=(log_e a-log_e1) + (log_e b-log_e1)` |
| `log_e(ab)` | `=log_e a + log_e b` |
`text(Solution 2)`
`text(Define each specific function)`
`(text{i.e.}\ \ f(x) = 1/(x – 2))`
`text(Enter functional equation until)`
`text(CAS output is “true”.)`
`=> E`
Let `f` be a differentiable function defined for all real `x`, where `f (x) >= 0` for all `x in [0, a].`
If `int_0^a f(x)\ dx = a`, then `2 int_0^(5a) (f (x/5) + 3)\ dx` is equal to
A. `2a + 6`
B. `10a + 6`
C. `20a`
D. `40a`
E. `50a`
`D`
`2 int_0^(5a) f(x/5) + 3\ dx`
`= 2 int_0^(5a) f(x/5)\ dx + 2 int_0^(5a) (3)\ dx`
`= 2 xx 5 [F(x/5)]_0^(5a) + [3x]_0^(5a)`
`= 10 [F(a) – F (0)] + 30a`
`= 10a + 30a`
`= 40a`
`=> D`
Consider the transformation `T`, defined as
`T: R^2 -> R^2, T([(x), (y)]) = [(−1, 0), (0, 3)][(x), (y)] + [(0), (5)]`
The transformation `T` maps the graph of `y = f (x)` onto the graph of `y = g(x).`
If `int_0^3 f(x)\ dx = 5`, then `int_-3^0 g(x)\ dx` is equal to
`E`
`text(Transformation taking)\ \ f -> g:`
`:. g(x) = 3 f(−x) + 5`
| `int_-3^0 g(x)\ dx` | `= int_-3^0 (3 f(−x) + 5)\ dx` |
| `= 3 int_-3^0 f(−x)\ dx + int_-3^0 5\ dx` | |
| `=3 int_0^3 f(x)\ dx + [5x]_-3^0` | |
| `= 3(5) + 15` | |
| `= 30` |
`=> E`
Consider the discrete probability distribution with random variable `X` shown in the table below.
The smallest and largest possible values of `text(E)(X)` are respectively
`E`
`text(Smallest)\ text(E)(X)\ \ text(occurs when)\ \ a=0.8,`
| `:.\ text(Smallest)\ text(E)(X)` | `=0.8 xx -1 + 0.2 xx 4` |
| `=0` |
`text(Consider the value of)\ b,`
`text(Sum of probabilities) = 1`
`:. 0 <= 4b <= 0.8 \ => \ 0 <= b <= 0.2`
`text(Largest)\ text(E)(X)\ \ text(occurs when)\ \ a=0, and b=0.2,`
`:.\ text(Largest)\ text(E)(X)`
`=0.2 xx 0 + 0.2 xx 0.2+(2xx0.2)xx(2xx0.2)+0.2 xx 4`
`=0.04 + 0.16 + 0.8`
`=1`
`=> E`
For two events, `P` and `Q`, `text(Pr)(P ∩ Q) = text(Pr)(P′ ∩ Q)`.
`P` and `Q` will be independent events exactly when
`=> E`
A new skateboard park is to be built in Beachton.
This project involves 13 activities, `A` to `M`.
The directed network below shows these activities and their completion times in days.
--- 2 WORK AREA LINES (style=lined) ---
Write down the critical path for this project. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
The cost of reducing the completion time by one day for these activities is shown in the table below.
What is the minimum cost to complete the project in the shortest time possible? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
The new activity, `N`, will take six days to complete and has a float time of one day.
Activity `N` will finish at the same time as the project.
i. Add activity `N` to the network below. (1 mark)
--- 0 WORK AREA LINES (style=lined) ---

ii. What is the latest start time for activity `N`? (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
| a. | `text(EST)` | `= 1 + 4 + 6` |
| `= 11\ text(days)` |
b. `text(Critical Path:)\ AEIK`
c. `text(Activity)\ H`
d. `text(Minimum days to complete is 14 days by reducing)`
`text(either)\ E\ text(or)\ I\ text(by 1 day.)`
`:. text(Minimum cost of $2000 when activity)\ I\ text(is reduced)`
`text(by 1 day.)`
| e.i. |
| e.ii. | `text(LST)` | `=\ text(critical path time − 6 days)` |
| `= 15-6` | ||
| `= 9\ text(days from the start.)` |
A company produces two types of hockey stick, the ‘Flick’ and the ‘Jink’.
Let `x` be the number of Flick hockey sticks that are produced each month.
Let `y` be the number of Jink hockey sticks that are produced each month.
Each month, up to 500 hockey sticks in total can be produced.
The inequalities below represent constraints on the number of each hockey stick that can be produced each month.
| Constraint 1 | `x >= 0` | Constraint 2 | `y >= 0` |
| Constraint 3 | `x + y <= 500` | Constraint 4 | `y <= 2x` |
There is another constraint, Constraint 5, on the number of each hockey stick that can be produced each month.
Constraint 5 is bounded by Line `A`, shown on the graph below.
The shaded region of the graph contains the points that satisfy constraints 1 to 5.
The profit, `P`, that the company makes from the sale of the hockey sticks is given by
`P = 62x + 86y`
The profit made on the Flick hockey sticks is `m` dollars per hockey stick.
The profit made on the Jink hockey sticks is `n` dollars per hockey stick.
The maximum profit of $42 000 is made by selling 400 Flick hockey sticks and 100 Jink hockey sticks.
What are the values of `m` and `n`? (2 marks)
a. `text(Constraint 4 means the number of Jink sticks)`
`text(produced each month is less than or equal to)`
`text(twice the number of flick sticks produced each)`
`text(month.)`
b. `y <= 300`
c. `text(From the equation, 1 Jink stick produces a)`
`text(higher profit than 1 Flick stick.)`
`text(Maximum profit at)\ (200,300)`
| `P` | `= (62 xx 200) + (86 xx 300)` |
| `= $38\ 200` |
d. `Q = mx + ny`
`text(Max profit at)\ (400,100)`
`(400,100)\ text(lies on)\ x + y = 500`
`=>\ text(Max profit equation has the same)`
`text(gradient as the profit line.)`
`=> m = −1, m = n`
`text(Using the maximum profit = $42 000,)`
| `400m + 100n` | `= 42\ 000` |
| `500m` | `= 42\ 000` |
| `m` | `= (42\ 000)/500` |
| `= 84` |
`:. m = n = 84`
A travel company is studying the choice between air (`A`), land (`L`), sea (`S`) or no (`N`) travel by some of its customers each year.
Matrix `T`, shown below, contains the percentages of customers who are expected to change their choice of travel from year to year.
`{:(qquadqquadqquadqquadqquadquadtext(this year)),(qquadqquadqquadquadAqquadqquadLqquadqquadSqquadquadN),(T = [(0.65,0.25,0.25,0.50),(0.15,0.60,0.20,0.15),(0.05,0.10,0.25,0.20),(0.15,0.05,0.30,0.15)]{:(A),(L),(S),(N):}text(next year)):}`
Let `S_n` be the matrix that shows the number of customers who choose each type of travel `n` years after 2014.
Matrix `S_0` below shows the number of customers who chose each type of travel in 2014.
`S_0 = [(520),(320),(80),(80)]{:(A),(L),(S),(N):}`
Matrix `S_1` below shows the number of customers who chose each type of travel in 2015.
`S_1 = TS_0 = [(478),(d),(e),(f)]{:(A),(L),(S),(N):}`
--- 2 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
In 2016, the number of customers studied was increased to 1360.
Matrix `R_2016`, shown below, contains the number of these customers who chose each type of travel in 2016.
`R_2016 = [(646),(465),(164),(85)]{:(A),(L),(S),(N):}`
`R_2017 = TR_2016 + BqquadqquadqquadR_2018 = TR_2017 + B`
`{:(qquadqquadqquadqquadqquadquadtext(this year)),(qquadqquadqquadquadAqquadqquadLqquadqquadSqquadquadN),(T = [(0.65,0.25,0.25,0.50),(0.15,0.60,0.20,0.15),(0.05,0.10,0.25,0.20),(0.15,0.05,0.30,0.15)]{:(A),(L),(S),(N):}text(next year)):}qquadqquad{:(),(),(B = [(80),(80),(40),(−80)]{:(A),(L),(S),(N):}):}`
--- 2 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
a. `d=298, \ e=94, \ f=130`
b. `(0.65 xx 520) + (0.25 xx 320) + (0.25 xx 80) + (0.50 xx 80) = 478`
c. `text(Sea Travel in 2014-80 customers.)`
`text(Of those 80 customers,)`
| `text(Sea Travel in 2015)` | `= 25text(%) xx 80` |
| `= 20\ text(customers)` |
d. `text(Expected total for air travel in 2015)`
`= 478\ text(customers)`
`text(In 2014, 520 customers chose air travel.)`
`text(65% of those chose air travel in 2015)`
`= 65text(%) xx 520`
`= 338\ text(customers)`
| `:.\ text(Percentage)` | `= 338/478 xx 100` |
| `= 70.71…` | |
| `= 71text(%)` |
e.i. `text(80 customers who have no travel in a given)`
`text(year are removed from the study. This occurs)`
`text(in both 2017 and 2018.)`
| e.ii. | `R_2017` | `= TR_2016 + B` |
| `= [(0.65,0.25,0.25,0.50),(0.15,0.60,0.20,0.15),(0.05,0.10,0.25,0.20),(0.15,0.05,0.30,0.15)][(646),(465),(164),(85)] + [(80),(80),(40),(−80)]` | ||
| `= [(699.65),(501.45),(176.80),(102.10)]` |
| `R_2018` | `= TR_2017 + B` |
| `= [(0.65,0.25,0.25,0.50),(0.15,0.60,0.20,0.15),(0.05,0.10,0.25,0.20),(0.15,0.05,0.30,0.15)][(699.65),(501.45),(176.80),(102.10)]` | |
| `= [(755.39),(536.49),(189.75),(118.38)]` |
`:. 190\ text(customers are expected to choose)`
`text(sea travel in 2018.)`
A golf course has a sprinkler system that waters the grass in the shape of a sector, as shown in the diagram below.
A sprinkler is positioned at point `S` and can turn through an angle of 100°.
The shaded area on the diagram shows the area of grass that is watered by the sprinkler.
Round your answer to the nearest metre. (1 mark)
This sprinkler will water a section of grass as shown in the diagram below.
The section of grass that is watered is 4.5 m wide at all points.
Water can reach a maximum of 12 m from the sprinkler at `L`.
What is the area of grass that this sprinkler will water?
Round your answer to the nearest square metre. (2 marks)
| a. | `text(Area of sector)` | `= theta/360 xx pi xx r^2` |
| `147.5` | `= 100/360 xx pi xx d^2` | |
| `d^2` | `= 147.5/pi xx 360/100` | |
| `= 169.02…` | ||
| `:.d` | `= 13.00…` | |
| `= 13\ text{m (nearest m)}` |
| b. | `text(Area)` | `= ((360 – theta))/360 xx pi xx R^2 – ((360 – theta))/360 xx pi xx r^2` |
| `= 260/360 xx pi (12^2 – 7.5^2)` | ||
| `= 199.09…` | ||
| `= 199\ text{m² (nearest m²)}` |
During a game of golf, Salena hits a ball twice, from `P` to `Q` and then from `Q` to `R`.
The path of the ball after each hit is shown in the diagram below.
After Salena’s first hit, the ball travelled 80 m on a bearing of 130° from point `P` to point `Q`.
After Salena’s second hit, the ball travelled 100 m on a bearing of 054° from point `Q` to point `R`.
Use the cosine rule to find the distance travelled by this ball.
Round your answer to the nearest metre. (2 marks)
Round your answer to the nearest degree. (1 mark)
| a. |  |
| `PR^2` | `= PQ^2 + QR^2 – 2 xx PQ xx QR xx cos104^@` |
| `= 80^2 + 100^2 – 2 xx 80 xx 100 xx cos104^@` | |
| `= 20\ 270.75…` | |
| `= 142.37…` | |
| `= 142\ text{m (nearest m)}` |
b. `text(Find)\ angle RPQ.`
`text(Using the sin rule),`
| `(sin angleRPQ)/100` | `= (sin104^@)/142` |
| `sin angle RPQ` | `= (100 xx sin104^@)/142` |
| `= 0.683…` | |
| `angle RPQ` | `= 43.1^@\ \ (text(1 d.p.))` |
`:. text(Bearing of)\ R\ text(from)\ P`
`= 130 – 43.1`
`= 086.9`
`= 087^@\ \ (text(nearest degree))`
Ken has borrowed $70 000 to buy a new caravan. He will be charged interest at the rate of 6.9% per annum, compounding monthly. --- 3 WORK AREA LINES (style=lined) --- --- 4 WORK AREA LINES (style=lined) --- --- 5 WORK AREA LINES (style=lined) ---
a.i.`$65\ 076.22` a.ii.`$4676.22` b. `$28\ 204.02`
a.i. `text(By TVM Solver,)` `:.\ text(Ken will owe $65 076.22)` `=> FV = 54\ 151.60` `text(fully repaid by monthly payments)` `text(of $800 over 3 years.)`
`N`
`= 12`
`I(%)`
`= 6.9`
`PV`
`= 70\ 000`
`PMT`
`= -800`
`FV`
`= ?`
`text(P/Y)`
`= text(C/Y) = 12`
`=> FV = -65\ 076.219…`
a.ii.
`text(Total interest paid)`
`= text(Total repayments) – text(reduction in principal)`
`= (12 xx 800) – (70\ 000 – 65\ 076.22)`
`= $4676.22`
b. `text(Find the loan balance after 3 years)`
MARKER’S COMMENT: Correct input tables allowed for a method mark if answers were calculated incorrectly.
`N`
`= 12 xx 3 = 36`
`I(%)`
`= 6.9`
`PV`
`= 70\ 000`
`PMT`
`= -800`
`FV`
`= ?`
`text(P/Y)`
`=text(C/Y)=12`
`text(Find the loan amount that can be)`
`N`
`= 36`
`I(%)`
`= 6.9`
`PV`
`= ?`
`PMT`
`= -800`
`FV`
`= 0`
`text(P/Y)`
`= text(C/Y)= 0`
`=> PV = 25\ 947.58`
`:.\ $L`
`= 54\ 151.60 -25\ 947.58`
`= $28\ 204.02`
Ken’s first caravan had a purchase price of $38 000.
After eight years, the value of the caravan was $16 000.
--- 2 WORK AREA LINES (style=lined) ---
Assume that the value of the caravan has been depreciated using the flat rate method of depreciation.
Write down a recurrence relation, in terms of `C_(n +1)` and `C_n`, that models the value of the caravan. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Assume that the value of the caravan has been depreciated using the unit cost method of depreciation.
By how much is the value of the caravan reduced per kilometre travelled? (1 mark)
--- 5 WORK AREA LINES (style=lined) ---
`= {(38\ 000-16\ 000)}/8`
`= $2750`
| b. | `C_0` | `= 38\ 000,` |
| `C_(n+1)` | `= C_n-2750` |
| c. | `text(Total kms travelled)` | `= 8 xx 5000` |
| `= 40\ 000` |
`:.\ text(Depreciation per km)`
`= {(38\ 000-16\ 000)}/(40\ 000)`
`= $0.55`
Five children, Alan, Brianna, Chamath, Deidre and Ewen, are each to be assigned a different job by their teacher. The table below shows the time, in minutes, that each child would take to complete each of the five jobs.
The teacher wants to allocate the jobs so as to minimise the total time taken to complete the five jobs.
In doing so, she finds that two allocations are possible.
If each child starts their allocated job at the same time, then the first child to finish could be either
`B`
The following graph with five vertices is a complete graph.
Edges are removed so that the graph will have the minimum number of edges to remain connected.
The number of edges that are removed is
`C`
Megan walks from her house to a shop that is 800 m away.
The equation for the relationship between the distance, in metres, that Megan is from her house `t` minutes after leaving is
`text(distance) = {(100t, 0 <= t <= 6),(\ 600, 6 < t <= a),(quadkt, a < t <= 10):}`
If Megan reaches the shop 10 minutes after leaving her house, the value of `a` is
`B`
`text(When)\ t = 10, d = 800`
| `800` | `= 10k` |
| `k` | `= 80` |
`text(From the equations and using)\ \ k=80,`
| `80a` | `= 600` |
| `:. a` | `= 600/80` |
| `= 7.5` |
`=> B`
The point (2, 12) lies on the graph of `y = kx^n`, as shown below.
Another graph that represents this relationship between `y` and `x` could be
`E`
`text(Consider each option,)`
`text(Option)\ A:\ text(graph between)\ x\ text(and)\ y\ text(cannot be linear.)`
`text(Option)\ B:\ y = 6x^2`
`text(Test)\ (2,12):\ 6 xx 2^2 = 24 != 12`
`text(Option)\ C:\ y = 3/2 x^2`
`text(Test)\ (2,12):\ 3/2 xx 2^2 = 6 != 12`
`text(Option)\ D:\ y = 6x^3`
`text(Test)\ (2,12):\ 6 xx 2^3 = 48 != 12`
`text(Option)\ E:\ y = 3/2 x^3`
`text(Test)\ (2,12):\ 3/2 xx 2^3 = 12`
`=> E`
The feasible region for a linear programming problem is shaded in the diagram below.
The equation of the objective function for this problem is of the form
`P = ax + by`, where `a > 0` and `b > 0`
The dotted line in the diagram has the same slope as the objective function for this problem.
The maximum value of the objective function can be determined by calculating its value at
`C`
`text(By applying the sliding rule technique)`
`text{(moving the objective function out in}`
`text{a series of parallel lines), the maximum}`
`text(value occurs at point)\ C.`
`=> C`
A string of seven flags consisting of equilateral triangles in two sizes is hanging at the end of a racetrack, as shown in the diagram below.
The edge length of each black flag is twice the edge length of each white flag.
For this string of seven flags, the total area of the black flags would be
`D`
`text(Shapes are similar.)`
`text(Scale factor of sides = 2)`
`text(Scale factor of areas) = 2^2 = 4`
`text(S)text(ince there are 4 black and 3)`
`text(white flags,)`
`:.\ text{Total area of black flags (in white flags)}`
`= 4/3 xx 4`
`= 16/3 xx text(Area of white flags)`
`=> D`
All towns in the state of Victoria are in the same time zone.
Mallacoota (38°S, 150°E) and Portland (38°S, 142°E) are two coastal towns in the state of Victoria.
On one day in January, the sun rose in Mallacoota at 6.03 am.
Assuming that 15° of longitude equates to a one-hour time difference, the time that the sun was expected to rise in Portland is
`E`
| `text(Angular difference)` | `= 150 – 142` |
| `= 8^@` |
| `text(Time difference)` | `= 8/15 xx 60` |
| `= 32\ text(minutes)` |
`text(S)text(ince Portland is West of Mallacoota,)`
`text(it’s sunrise will be later.)`
| `:.\ text(Portland)` | `= 6:03 + 32\ text(minutes)` |
| `= 6:35\ text(am)` |
`=> E`
Mai invests in an annuity that earns interest at the rate of 5.2% per annum compounding monthly.
Monthly payments are received from the annuity.
The balance of the annuity will be $130 784.93 after five years.
The balance of the annuity will be $66 992.27 after 10 years.
The monthly payment that Mai receives from the annuity is closest to
`C`
`text(By TVM solver, starting at 5 years,)`
| `N` | `= 5 xx 12=60` |
| `I(text(%))` | `= 5.2` |
| `PV` | `= −130\ 784.93` |
| `PMT` | `= ?` |
| `FV` | `= 66\ 992.27` |
| `text(P/Y)` | `= text(C/Y) = 12` |
| `:. PMT` | `= 1500.00…` |
`=> C`
`text(Consider the surface area of each pool:)`
`text(1st pool) = 6 xx 19 = 114\ text(m²)`
`text(2nd pool) = 7 xx 18 = 126\ text(m²)`
`text(3rd pool) = 12.5 xx 12.5 = 156.25\ text(m²)`
`text(4th pool) =10 xx 15 = 150\ text(m²)`
`:.\ text(The 3rd pool, 12.5 × 12.5, has the largest)`
`text(surface area.)`
Jake makes a pattern with black and white balls.
Altogether, how many balls are needed for the 5th pattern?
| `13` | `14` | `15` | `18` |
|
|
|
|
|
`14`
`text(White ball pattern: 2, 3, 4, 5, 6 …)`
`text(Black ball pattern: 4, 5, 6, 7, 8, …)`
`:.\ text(Total balls in pattern 5)`
`=6\ text(white balls) + 8\ text(black balls)`
`=14\ text(balls)`
Jane and five of her friends share 2 cakes.
If all six friends share equally, what fraction of one cake does each of them get?
| `1/2` | `1/3` | `1/6` | `1/12` |
|
|
|
|
|
`1/3`
| `text(Fraction of 1 cake)` | `=2/6` |
| `=1/3` |
A group of soccer fans all go to a soccer game.
Entry to the game costs $3.
Altogether the group pay $156.
How many soccer fans are there in the group?
| `50` | `51` | `52` | `63` |
|
|
|
|
|
`52`
| `text(Fans in group)` | `=156 -: 3` |
| `=52` |
5 boys win $3.
They share the money equally.
How much does each boy get?
| cents |
`60¢`
| `$3 ÷ 5` | `= 300¢ ÷ 5` |
| `= 60¢` |
`=>\ text(Each boy gets)\ 60¢`
Percy buys a cricket ball and a set of stumps.
The total cost is $23.
The stumps cost $3 more than the ball.
What is the cost of the ball?
| $ |
`$10`
`text(Test some numbers:)`
`text(Stumps $12 – Ball $11)`
`= $1\ text(difference)`
`text(Stumps $13 – Ball $10)`
`= $3\ text(difference)`
`=>\ text(The ball must cost $10.)`
Kim started at 5 and made this number pattern
| `5, 6, 8, 11, 15, 20,` |
|
What is the next number in the pattern?
| `21` | `25` | `26` | `30` |
|
|
|
|
|
`26`
`text(The difference between each number increases)`
`text(by 1 each time.)`
| `5+1` | `=6` |
| `6+2` | `=8` |
| `vdots\ \ ` | |
| `20+6` | `=26` |
`=>\ text(The next number is 26.)`