Eric owns a book which has more than 258 pages but less than 285 pages
Which of these could represent the number of pages in Eric’s book?
| 287 | 294 | 249 | 262 |
|
|
|
|
|
Aussie Maths & Science Teachers: Save your time with SmarterEd
Eric owns a book which has more than 258 pages but less than 285 pages
Which of these could represent the number of pages in Eric’s book?
| 287 | 294 | 249 | 262 |
|
|
|
|
|
`262`
`text{Check each option:}`
`text{287 is more than 285 ⇒ incorrect}`
`text{294 is more than 285 ⇒ incorrect}`
`text{249 is less than 258 ⇒ incorrect}`
`text{262 is more than 258 and less than 285 ⇒ correct}`
i. `A(3, 0 , 0), \ \ G(0, 3, 3)`
`vec(AG)`
`= ((0), (3), (3))-((3), (0), (0)) = ((text{−3}), (3), (3))`
`|\ vec(AG)\ |`
`= sqrt (9 + 9 + 9)`
`= 3 sqrt 3\ text(units)`
ii.
`H (3, 3, 3)`
`vec(BH) = ((3), (3), (3))`
`vec(AG) ⋅ vec(BH)`
`= |\ vec(AG)\ | ⋅ |\ vec(BH)\ |\ cos theta`
`((text{−3}), (3), (3)) ⋅ ((3), (3), (3))`
`= sqrt (9 + 9 + 9) ⋅ sqrt (9 + 9 + 9) cos theta`
`-9 + 9 + 9`
`= 27 cos theta`
`cos theta`
`= 1/3`
`theta`
`= 70.52…`
`= 70^@32′`
The delivery fee for a parcel, in dollars, charged by a courier company is based on the weight of the parcel, in kilograms.
This relationship is shown in the step graph below for parcels that weigh up to 20 kg.
Which one of the following statements is not true?
`E`
`text(Consider option)\ E:`
`text(Delivery fee for 12kg parcel) = $26`
`text(Delivery fee for 2kg parcel) = $12\ text{($14 difference)}`
`:.\ text(Statement)\ E\ text(is correct.)`
`=> E`
Two trees stand on horizontal ground.
A 25 m cable connects the two trees at point A and point B, as shown in the diagram below.
Point A is 45 m above the ground and point B is 30 m above the ground.
The horizontal distance, in metres, between point A and point B is
`C`
A flag consists of three different coloured sections: red, white and blue.
The flag is 3 m long and 2 m wide, as shown in the diagram below.
The blue section is an isosceles triangle that extends to half the length of the flag.
The area of the blue section, in square metres, is
`B`
| `text(Area)` | `= 1/2 xx 2 xx 1.5` |
| `= 1.5\ text(m²)` |
`=> B`
Consider the graph below.
Which one of the following is not a Hamiltonian cycle for this graph?
`D`
`text(Hamiltonian cycle – start and finish at the same)`
`text(vertex and touch all other vertices once.)`
`text(Option)\ D\ text(is not a valid path as it needs an edge)\ E\ text(to)\ D.`
`=> D`
A connected planar graph has seven vertices and nine edges.
The number of faces that this graph will have is
`D`
| `v + f ` | `= e + 2` |
| `7 + f ` | `= 11` |
| `f` | `= 4` |
`=> D`
The diagram below shows the direct communication links that exist between Sam (S), Tai (T), Umi (U) and Vera (V). For example, the arrow from Umi to Vera indicates that Umi can communicate directly with Vera.
A communication matrix can be used to convey the same information.
In this matrix:
The communication matrix could be
| A. |
`{:(qquadqquadqquadqquadqquadqquadquad receiver),(\ quad qquadqquadqquadqquad qquadS\ \ \ Tquad U\ \ V),(sender qquad{:(S),(T),(U),(V):}[(0,1,0,1),(0,0,0,1),(0,1,0,1),(1,0,1,0)]):}`
|
B. |
`{:(qquadqquadqquadqquadqquadqquadquad receiver),(\ quad qquadqquadqquadqquad qquadS\ \ \ Tquad U\ \ V),(sender qquad{:(S),(T),(U),(V):}[(0,1,0,1),(1,0,0,1),(0,1,0,1),(1,1,1,0)]):}`
|
| C. |
`{:(qquadqquadqquadqquadqquadqquadquad receiver),(\ quad qquadqquadqquadqquad qquadS\ \ \ Tquad U\ \ V),(sender qquad{:(S),(T),(U),(V):}[(0,1,0,1),(0,0,0,1),(0,1,0,0),(1,1,1,0)]):}`
|
D. |
`{:(qquadqquadqquadqquadqquadqquadquad receiver),(\ quad qquadqquadqquadqquad qquadS\ \ \ Tquad U\ \ V),(sender qquad{:(S),(T),(U),(V):}[(0,1,0,1),(0,0,0,1),(0,1,0,1),(1,1,1,0)]):}`
|
| E. |
`{:(qquadqquadqquadqquadqquadqquadquad receiver),(\ quad qquadqquadqquadqquad qquadS\ \ \ Tquad U\ \ V),(sender qquad{:(S),(T),(U),(V):}[(0,1,0,2),(0,0,0,2),(0,1,0,2),(2,2,2,0)]):}`
|
`D`
`text(By Elimination):`
`text(Vera can talk to Tai) \ => \ e_42 = 1`
`:.\ text(Eliminate)\ A and E`
`text(Umi can talk to Vera) \ => \ e_34 = 1`
`:.\ text(Eliminate)\ C`
`text(Tai cannot talk to Sam) \ => \ e_21 = 0`
`:.\ text(Eliminate)\ B`
`=> D`
In a particular supermarket, the three top-selling magazines are Angel (A), Bella (B) and Crystal (C).
The transition diagram below shows the way shoppers at this supermarket change their magazine choice from week to week.
A transition matrix that provides the same information as the transition diagram is
| A. |
`{:(qquadqquadquad this\ week),(qquadquadAqquadquad\ Bqquadquad\ C),([(0.55,0.70,0.35),(0.70,0.60,0.40),(0.35,0.40,0.40)]{:(A),(B),(C):}qquad n\ext\ week):}`
|
B. |
`{:(qquadqquadquad this\ week),(qquadquadAqquadquad\ Bqquadquad\ C),([(0.55,0.60,0.25),(0.45,0.15,0.35),(0,0.25,0.40)]{:(A),(B),(C):} qquad n\ext\ week):}`
|
| C. |
`{:(qquadqquadquad this\ week),(qquadquadAqquadquad\ Bqquadquad\ C),([(0.55,0.25,0.35),(0.45,0.60,0.25),(0,0.15,0.40)]{:(A),(B),(C):} qquad n\ext\ week):}`
|
D. |
`{:(qquadqquadquad this\ week),(qquadquadAqquadquad\ Bqquadquad\ C),([(0.55,0.25,0.35),(0.45,0.60,0.25),(0.35,0.15,0.40)]{:(A),(B),(C):} qquad n\ext\ week):}`
|
| E. |
`{:(qquadqquadquad this\ week),(qquadquadAqquadquad\ Bqquadquad\ C),([(0.55,0.25,0),(0.45,0.60,0.25),(0,0.15,0.75)]{:(A),(B),(C):} qquad n\ext\ week):}`
|
`C`
`text(By Elimination):`
`25text(%)\ text(of)\ B\ text(moves to)\ A \ => \ e_12 = 0.25`
`:.\ text(Eliminate)\ A and B`
`C\ text(retains 40% from week to week)\ => \ e_33 = 0.4`
`:.\ text(Eliminate)\ E`
`0text(%)\ text(of)\ A\ text(moves to)\ C \ => \ e_31 = 0`
`:.\ text(Eliminate)\ D`
`=> C`
Matrix `A = [(1, 2), (0, 3), (1, 0), (4, 5)]` and matrix `B = [(2, 0, 3, 1), (4, 5, 2, 0)]`.
Matrix `Q = A xx B`.
The element in row `i` and column `j` of matrix `Q` is `q_(ij)`.
Element `q_41` is determined by the calculation
`E`
`Q = [(1, 2), (0, 3), (1, 0), (4, 5)][(2, 0, 3, 1), (4, 5, 2, 0)]`
`q_41 = 4 xx 2 + 5 xx 4`
`=> E`
The matrix `[(1, 0, 0), (0, 1, 1), (1, 0, 1)]` is an example of
`A`
`text(All elements are 0 or 1 and other definitions)`
`text(don’t apply.)`
`=> A`
Manu invests $3000 in an account that pays interest compounding monthly.
The balance of his investment after `n` months, `B_n` , can be determined using the recurrence relation
`B_0 = 3000, qquad B_(n+1) = 1.0048 xx B_n`
The total interest earned by Manu’s investment after the first five months is closest to
`D`
| `text(Total interest)` | `= 3000 xx 1.0048^5 – 3000` |
| `~~ $72.69` |
`=> D`
Consider the following four recurrence relations representing the value of an asset after `n` years, `V_n`.
How many of these recurrence relations indicate that the value of an asset is depreciating?
`C`
| `V_(n+1)` | `= V_n + 2500\ => \ text(appreciating)` |
| `V_(n-1)` | `= V_n – 2500\ => \ text(depreciating)` |
| `V_(n+1)` | `= 0.875 V_n\ => \ text(depreciating)` |
`text(When)\ \ V_(n+1) = 1.125 V_n – 2500`
| `V_1` | `= 1.125 xx 20\ 000 – 2500` |
| `= 20\ 000\ text{(same price)}` |
`=> C`
The following recurrence relation can generate a sequence of numbers.
`T_0 = 10, qquad T_(n + 1) = T_n + 3`
The number 13 appears in this sequence as
`A`
`text(If)\ \ n = 0:`
| `T_1` | `= T_0 + 3` |
| `= 10 + 3` | |
| `= 13` |
`=> A`
Table 4 below shows the monthly rainfall for 2019, in millimetres, recorded at a weather station, and the associated long-term seasonal indices for each month of the year.
Part 1
The deseasonalised rainfall for May 2019 is closest to
Part 2
The six-mean smoothed monthly rainfall with centring for August 2019 is closest to
`text(Part 1:)\ B`
`text(Part 2:)\ C`
Part 1
`text(Deseasonalised rainfall for May)`
`= 92.6/1.222`
`= 75.8\ text(mm)`
`=> B`
Part 2
`text{Six-mean smoothed average (Aug)}`
`=[(92.6 + 77.2 + 80 + 86.8 + 93.8 + 55.2) ÷6 +`
`(77.2 + 80 + 86.8 + 93.8 + 55.2 + 97.3) ÷ 6] ÷ 2`
`~~ (80.93 + 81.72) ÷ 2`
`~~ 81.3\ text(mm)`
`=> C`
The times between successive nerve impulses (time), in milliseconds, were recorded.
Table 1 shows the mean and the five-number summary calculated using 800 recorded data values.
Part 1
The difference, in milliseconds, between the mean time and the median time is
Part 2
Of these 800 times, the number of times that are longer than 300 milliseconds is closest to
Part 3
The shape of the distribution of these 800 times is best described as
`text(Part 1:)\ B`
`text(Part 2:)\ D`
`text(Part 3:)\ C`
Part 1
| `text(Difference)` | `= 220 -150` |
| `= 70` |
`=> B`
Part 2
`Q_3 = 300`
`:.\ text(Impulses longer than 300 milliseconds)`
`= 25text(%) xx 800`
`= 200`
`=> D`
Part 3
`text(Distribution has a long tail to the right)`
`:.\ text(Positively skewed)`
| `text(Upper fence)` | `= Q_3 + 1.5 xx IQR` |
| `= 300 + 1.5 (300 – 70)` | |
| `= 645` |
`=> C`
Let `f(x) = tan^(-1) (3x - 6) + pi`.
--- 2 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
--- 0 WORK AREA LINES (style=lined) ---
| a. | `f^{\prime}(x)` | `= (d/(dx) (3x – 6))/(1 + (3x – 6)^2)` |
| `= 3/(9x^2 – 36x + 37)` |
b. `f^{\prime\prime}(x) = (3(18x – 36))/(9x^2 – 36x + 37)^2`
`f^{\prime\prime}(x) = 0\ \ text(when)\ \ 18x – 36 = 0 \ => \ x = 2`
`text(If)\ \ x < 2, 18x – 36 < 0 \ => \ f^{\prime\prime}(x) < 0`
`text(If)\ \ x > 2, 18x – 36 > 0 \ => \ f^{\prime\prime}(x) > 0`
`text(S) text(ince)\ \ f^{\prime\prime}(x)\ \ text(changes sign about)\ \ x = 2,`
`text(a POI exists at)\ \ x = 2`
| c. |
Let `f(x) = arctan (3x - 6) + pi`. --- 2 WORK AREA LINES (style=lined) --- --- 5 WORK AREA LINES (style=lined) --- --- 0 WORK AREA LINES (style=lined) ---
b. `f^{\prime\prime}(x) = (3(18x – 36))/(9x^2 – 36x + 37)^2` `f^{\prime\prime}(x) = 0\ \ text(when)\ \ 18x – 36 = 0 \ => \ x = 2` `text(If)\ \ x < 2, 18x – 36 < 0 \ => \ f^{\prime\prime}(x) < 0` `text(If)\ \ x > 2, 18x – 36 > 0 \ => \ f^{\prime\prime}(x) > 0` `text(S) text(ince)\ \ f^{\prime\prime}(x)\ \ text(changes sign about)\ \ x = 2,` `text(a POI exists at)\ \ x = 2`
a.
`f^{\prime}(x)`
`= (d/(dx) (3x – 6))/(1 + (3x – 6)^2)`
`= 3/(9x^2 – 36x + 37)`
c.
Evaluate `int_(-1)^0 (1 + x)/sqrt(1 - x)\ dx`, using the substitution `u=1-x`. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
`(8 sqrt 2)/3 – 10/3`
| `u` | `= 1 – x \ => \ x = 1 – u` |
| `(du)/(dx)` | `= -1 \ => \ dx = -du` |
| `text(When)\ \ x` | `= 0,\ u = 1` |
| `x` | `= -1,\ u = 2` |
| `int_(-1)^0 (1 + x)/sqrt(1 – x)\ dx` | `= -int_2^1 (2 – u)/sqrt u\ du` |
| `= int_1^2 2u^(-1/2) – u^(1/2)\ du` | |
| `= [4u^(1/2) – 2/3u^(3/2)]_1^2` | |
| `= 4 sqrt 2 – (4 sqrt 2)/3 – (4 – 2/3)` | |
| `= (8 sqrt 2)/3 – 10/3` |
Evaluate `int_(-1)^0 (1 + x)/sqrt(1 - x)\ dx`. (3 marks)
--- 8 WORK AREA LINES (style=lined) ---
`(8 sqrt 2)/3 – 10/3`
| `text(Let)\ \ u` | `= 1 – x \ => \ x = 1 – u` |
| `(du)/(dx)` | `= -1 \ => \ dx = -du` |
| `text(When)\ \ x` | `= 0,\ u = 1` |
| `x` | `= -1,\ u = 2` |
| `int_(-1)^0 (1 + x)/sqrt(1 – x)\ dx` | `= -int_2^1 (2 – u)/sqrt u\ du` |
| `= int_1^2 2u^(-1/2) – u^(1/2)\ du` | |
| `= [4u^(1/2) – 2/3u^(3/2)]_1^2` | |
| `= 4 sqrt 2 – (4 sqrt 2)/3 – (4 – 2/3)` | |
| `= (8 sqrt 2)/3 – 10/3` |
Consider the function `f(x) = x^2 + 3x + 5` and the point `P(1, 0)`. Part of the graph `y = f(x)` is shown below.
--- 2 WORK AREA LINES (style=lined) ---
i. Find the slope of the line connecting points `P` and `Q` in terms of `a`. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
ii. Find the slope of the tangent to the graph of `f` at point `Q` in terms of `a`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
iii. Let the tangent to the graph of `f` at `x = a` pass through point `P`.
Find the values of `a`. (2 marks)
--- 7 WORK AREA LINES (style=lined) ---
iv. Give the equation of one of the lines passing through point `P` that is tangent to the graph of `f`. (1 mark)
--- 6 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
a. `f(1) = 1 + 3 + 5 = 9`
`text(S)text(ince)\ \ f(1) != 0, P(1, 0)\ text(does not lie on)\ \ y = f(x)`
b.i. `P(1, 0), Q(a, f(a))`
| `m_(PQ)` | `= (f(a)-0)/(a-1)` |
| `= (a^2 + 3a + 5)/(a-1)` |
b.ii. `f^{prime}(x) = 2x + 3`
`m_Q = f^{prime}(a) = 2a + 3`
b.iii. `text(T)text(angent:)\ m = 2a + 3,\ text(passes through)\ (a, a^2 + 3a + 5)`
`y-(a^2 + 3a + 5) = (2a + 3)(x-1)`
`text(Passes through)\ P(1, 0):`
| `0-(a^2 + 3a + 5)` | `= (2a + 3)(1-a)` |
| `-(a^2 + 3a + 5)` | `= 2a-2a^2 + 3-3a` |
| `a^2-2a-8` | `= 0` |
| `(a-4)(1 + 2)` | `= 0` |
`:. a = 4\ text(or)\ -2`
b.iv. `text(When)\ \ a = -2`
`m_text(tang) = 2x-2 + 3 = -1`
`text(Equation of line)\ \ m =-1,\ text(through)\ P(1, 0)`
| `y-a` | `=-1(x-1)` |
| `y` | `= -x + 1` |
`text(Similarly, if)\ \ a = 4:`
`y = 11x-11`
c. `f(x)\ text(is a quadratic with no roots.`
`text(Shortest distance needs S.P. to occur when)\ \ x = 1`
`f^{prime}(x) = 2x + 3`
`text(MIN S.P. of)\ \ f(x)\ \ text(occurs when)\ \ f^{prime}(x) = 0`
`x =-3/2`
`f(-2/3-k) = f(1)\ \ text(for shortest distance.)`
`:. k = 5/2`
Differentiate with respect to `x`:
Let `y=sin x/(x + 1)`. Find `dy/dx `. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
`dy/dx = {cos x (x + 1)-sin x} / (x + 1)^2`
`y = sinx/(x + 1)`
`d/dx (u/v) = (u^{\prime} v-uv^{\prime})/v^2`
| `u` | `= sin x` | `v` | `= x + 1` |
| `u^{\prime}` | `= cos x` | `\ \ \ v^{\prime}` | `= 1` |
`:.dy/dx = {cos x (x + 1)-sin x} / (x + 1)^2`
Let `f(x) = e^(x^2)`.
Find `f^{\prime} (3)`. (3 marks)
--- 4 WORK AREA LINES (style=lined) ---
`6e^9`
`text(Using Chain Rule:)`
| `f^{\prime} (x)` | `= 2xe^(x^2)` |
| `f^{\prime} (3)` | `= 2 (3) e^((3)^2)` |
| `= 6e^9` |
For `f(x) = log_e (x^2 + 1)`, find `f^{\prime}(2)`. (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
`4/5`
`text(Using Chain Rule:)`
| `f ^{\prime}(x)` | `= (2x)/(x^2 + 1)` |
| `:. f ^{\prime}(2)` | `= (2(2))/(2^2 + 1)` |
| `= 4/5` |
Let `y=ln(3x^3 + 2)`.
Find `dy/dx`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
`2e^x(e^x + 1)`
| `y` | `=ln(3x^3 + 2)` | |
| `(dy)/(dx)` | `=(3*3x^2)/(3x^3 + 2)` | |
| `=(9x^2)/(3x^3 + 2)` |
Let `y= (x + 5) log_e (x)`.
Find `(dy)/(dx)` when `x = 5`. (2 marks)
`log_e 5 +2`
| `(dy)/(dx)` | `= 1 xx log_e x + (x + 5) * (1)/(x)` |
| `= log_e x + (x + 5)/(x)` |
`:. dy/dx|_(x=5)=log_e 5 +2`
Let `g(x) = (2-x^3)^3`.
Evaluate `g^{\prime}(1)`. (2 marks)
`g^{\prime}(1) = -9`
`text(Using Chain Rule:)`
| `g^{\prime}(x)` | `= 3 (2-x^3)^2 (-3x^2)` |
| `= -9x^2 (2-x^3)^2` | |
| `:. g^{\prime}(1)` | `= -9 (1) (2-1)^2` |
| `= -9` |
`f(x) = 1/sqrt2 sqrtx`, where `x in [0,2]`
--- 4 WORK AREA LINES (style=lined) ---
The graph of `y = f(x)`, where `x ∈ [0, 2]`, is shown on the axes below.
--- 0 WORK AREA LINES (style=lined) ---
`f^(-1)(x) = 2x^2`
a. `text(Domain)\ \ f^(-1)(x)= text(Range)\ \ f(x)=[0,1]`
`y = 1/sqrt2 x`
`text(Inverse: swap)\ \ x ↔ y`
| `x` | `= 1/sqrt2 sqrty` | |
| `sqrty` | `= sqrt2 x` | |
| `y` | `= 2x^2` |
`:. f^(-1)(x) = 2x^2`
| b. | |
A car manufacturer is reviewing the performance of its car model X. It is known that at any given six-month service, the probability of model X requiring an oil change is `17/20`, the probability of model X requiring an air filter change is `3/20` and the probability of model X requiring both is `1/20`.
--- 5 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
| a. |
| `text(Pr)(F ∩ O′)` | `= text(Pr)(F) – text(Pr)(F∩ O)` | |
| `= 3/20 – 1/20` | ||
| `= 1/10` |
| b. |
| `text(Pr)(F ∩ O′)` | `= n/(m + n) – 1/(m + n)` |
| `1/20` | `= (n – 1)/(m + n)` |
| `m + n` | `= 20n – 20` |
| `m` | `= 19n – 20` |
A car manufacturer is reviewing the performance of its car model X. It is known that at any given six-month service, the probability of model X requiring an oil change is `17/20`, the probability of model X requiring an air filter change is `3/20` and the probability of model X requiring both is `1/20`. --- 5 WORK AREA LINES (style=lined) --- --- 5 WORK AREA LINES (style=lined) ---
a.
`text(Pr)(F ∩ O′)`
`= text(Pr)(F) – text(Pr)(F∩ O)`
`= 3/20 – 1/20`
`= 1/10`
b.
`text(Pr)(F ∩ O′)`
`= n/(m + n) – 1/(m + n)`
`1/20`
`= (n – 1)/(m + n)`
`m + n`
`= 20n – 20`
`m`
`= 19n – 20`
Evaluate `f^{\prime}(1)`, where `f: R -> R, \ f(x) = e^(x^2-x + 3)`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
`e^3`
| `f(x)` | `= e^(x^2-x + 3)` |
| `f^{\prime}(x)` | `= (2x-1)e^(x^2-x + 3)` |
| `f^{\prime}(1)` | `= (2-1)e^(1-1 + 3)` |
| `= e^3` |
Let `y = x^2 sin(x)`.
Find `(dy)/(dx)`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
`2x sin(x) + x^2 cosx`
`(dy)/(dx) = 2x sin(x) + x^2 cosx`
Prove `sqrt5 + sqrt3 > sqrt14` by contradiction. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
`text(See Worked Solutions)`
`text(Proof by contradiction:)`
`text(Assume)\ \ sqrt5 + sqrt3 <= sqrt14`
| `(sqrt5 + sqrt3)^2` | `<= (sqrt14)^2` |
| `5 + 2sqrt15 + 3` | `<= 14` |
| `2sqrt15` | `<= 6` |
| `sqrt15` | `<= 3` |
| `15` | `<= 9\ \ \ text{(incorrect)}` |
`:. text(By contradiction,)\ sqrt5 + sqrt3 > sqrt14`
Let `z = sqrt3 - 3 i`
--- 6 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
| i. | `z` | `= sqrt3 – 3 i` |
| `|z|` | `= sqrt((sqrt3)^2 + 3^2) = 2 sqrt3` |
| `tan theta` | `= frac{3}{sqrt3}=sqrt3` |
| `theta` | `= frac{pi}{3}` |
| `text{arg} (z)` | `= – frac{pi}{3}` |
`therefore z = 2 sqrt3 \ text{cis} (frac{-pi}{3})`
ii. `z^n + (overset_z)^n = 0`
`[2 sqrt3 \ cos (frac{-pi}{3}) + i sin (frac{-pi}{3})]^n + [ 2 sqrt3 \ cos (frac{-pi}{3}) – i sin (frac{-pi}{3}) ]^n = 0`
`(2 sqrt3)^n [cos (frac{-n pi}{3}) + i sin (frac{-n pi}{3}) + cos (frac{-n pi}{3}) – i sin (frac{-n pi}{3}) = 0`
| `2 \ cos (frac{-n pi}{3})` | `= 0` |
| `cos (frac{n pi}{3})` | `= 0` |
| `frac{n pi}{3}` | `= frac{pi}{2} + k pi \ , \ k = 0, ± 1, ± 2, …` |
| `frac{n}{3}` | `= frac{(2k + 1)}{2}` |
| `n` | `= frac{3 (2k + 1)}{2}` |
`text{Numerator will always be odd ⇒ no solution exists}`
Which of the following is the complex number \(-\sqrt{3}+3 i ?\)?
\(B\)
| \(\abs{z}\) | \(=\sqrt{(\sqrt{3})^2+3^2}=2 \sqrt{3}\) |
| \(\tan \theta\) | \(=\dfrac{\sqrt{3}}{3}=\dfrac{1}{\sqrt{3}}\) |
| \(\theta\) | \(=\dfrac{\pi}{6}\) |
\(\arg (z)=\dfrac{\pi}{2}+\dfrac{\pi}{6}=\dfrac{2 \pi}{3}\)
| \(\therefore z\) | \(=2 \sqrt{3}\left(\cos \left(\dfrac{2 \pi}{3}\right)+i \sin \left(\dfrac{2 \pi}{3}\right)\right.\) |
| \(=2 \sqrt{3} e^{\small{\dfrac{i 2 \pi}{3}}}\) |
\(\Rightarrow B\)
Let `alpha = 1 + i sqrt3` and `beta = 1 + i`.
--- 3 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
| i. | `frac{alpha}{beta}` | `= frac{1 + i sqrt3}{1 + i} xx frac{1 – i}{1 – i}` |
| `= frac{(1 + i sqrt3)(1 – i)}{1^2 – i^2}` | ||
| `= frac{1 – i + i sqrt3 – i^2 sqrt3}{2}` | ||
| `= frac{1+sqrt3}{2} + i (frac{sqrt3 – 1}{2})` |
| ii. | `alpha` | `= 1 + i sqrt3` |
| `| alpha |` | `= sqrt(1^2 + (sqrt3)^2) = 2` |
`text{arg} \ (alpha) = tan^-1 (frac{sqrt3}{1}) = frac{pi}{3}`
`therefore \ alpha = 2 text{cis} (frac{pi}{3})`
| iii. | `beta` | `= sqrt2 text{cis} (frac{pi}{4})` |
| `frac{alpha}{beta}` | `= frac{2}{sqrt2} \ text{cis} (frac{pi}{3} – frac{pi}{4})` | |
| `= sqrt2 text{cis} (frac{pi}{12})` |
iv. `text{Equating imaginary parts of i and ii:}`
| `sqrt2 \ sin \ (frac{pi}{12})` | `= frac{sqrt3 – 1}{2}` |
| `sin (frac{pi}{12})` | `= frac{sqrt3 – 1}{2 sqrt2} xx frac{sqrt2}{sqrt2}` |
| `= frac{sqrt6 – sqrt2}{4}` |
`z = sqrt2 e^((ipi)/15)` is a root of the equation `z^5 = alpha(1 + isqrt3), \ alpha ∈ R`.
--- 4 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
i. `beta = 1 + isqrt3`
`|beta| = sqrt(1 + (sqrt3)^2) = 2`
`text(arg)(beta) = tan^(−1) (sqrt3/1) = pi/3`
`beta = 2e^((ipi)/3)`
| ii. | `z` | `= sqrt2 e^((ipi)/15)` |
| `z^5` | `= (sqrt2 e^((ipi)/15))^5` | |
| `= (sqrt2)^5 e^((ipi)/15 xx 5)` | ||
| `= 4sqrt2 e^((ipi)/3)` |
`:. alpha = 2sqrt2`
iii. `text(arg)(z^5) = pi/3 + 2kpi, \ \ k = 0, ±1, ±2, …`
`text(arg)(z) = pi/15 + (2kpi)/5`
`k = 1:\ text(arg)(z) = pi/15 + (2pi)/5 = (11pi)/15`
`k = text(−1):\ text(arg)(z) = pi/15 – (2pi)/5 = −pi/3`
`k = 2:\ text(arg)(z) = pi/15 + (4pi)/5 = (13pi)/15`
`k =text(−2):\ text(arg)(z) = pi/15 – (4pi)/5 = −(11pi)/15`
`:. 4\ text(other roots are:)`
`e^((i11pi)/15), e^(−(ipi)/3), e^((i13pi)/15), e^(−(i11pi)/15)`
Calculate the value of \(\dfrac{e^{\small{\dfrac{i \pi}{3}}}-e^{-\small{\dfrac{i \pi}{3}}}}{2 i}\). (2 marks)
\(\dfrac{\sqrt{3}}{2}\)
| \(\dfrac{e^{\small{\dfrac{i \pi}{3}}}-e^{-\small{\dfrac{i \pi}{3}}}}{2 i}\) | \(=\dfrac{\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}-\left(\cos \left(-\frac{\pi}{3}\right)+i \sin \left(-\frac{\pi}{3}\right)\right)}{2 i}\) |
| \(=\dfrac{\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}-\left(\cos \frac{\pi}{3}-i \sin \frac{\pi}{3}\right)}{2 i}\) | |
| \(=\dfrac{2 i \sin \frac{\pi}{3}}{2 i}\) | |
| \(=\sin \frac{\pi}{3}\) | |
| \(=\dfrac{\sqrt{3}}{2}\) |
In which quadrant of the complex plane is the complex number \(4e^{\small{\dfrac{i16}{3}}}\) found?
\(\D\)
\(z=4 e^{\small{\dfrac{in6}{3}}}\)
\(\arg (z)=\dfrac{16}{3} \approx 5.3\)
\(\dfrac{3 \pi}{2}<5.3<2 \pi\)
\(\therefore \ \text{Quadrant IV}\)
\(\Rightarrow D\)
Let `t=tan(theta/2).`
--- 3 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
| i. | `t` | `= tan frac{theta}{2}` |
| `frac{dt}{d theta}` | `= frac{1}{2} text{sec}^2 frac{theta}{2}` | |
| `= frac{1}{2} (1 + tan^2 frac{theta}{2})` | ||
| `= frac{1}{2} (1 + t^2)` |
ii. `text{Show} \ \ sin theta = frac{2t}{1 + t^2} :`
| `sin theta` | `= 2 \ sin frac{theta}{2} cos frac{theta}{2}` |
| `= 2 * frac{t}{sqrt(1 + t^2)} * frac{1}{sqrt(1 + t^2)}` | |
| `= frac{2t}{1 + t^2}` |
iii. `int \ text{cosec} \ theta \ d theta`
`t = tan frac {theta}{2}`
`frac{dt}{d theta} = frac{1}{2} text{sec}^2 frac{theta}{2} \ , \ d theta = frac{2dt}{sec^2 frac{theta}{2}} = frac{2}{1 + t^2} dt`
| `int \ text{cosec} \ theta\ d theta` | `= int frac{1 + t^2}{2t} xx frac{2}{1 + t^2} dt` |
| `= int frac{1}{t}\ dt` | |
| `= log_e | t | + c` | |
| `= log_e | tan frac{theta}{2} | + c` |
Let `beta = 1-i sqrt3`.
--- 6 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
i. `beta = 1 – i sqrt3`
`| beta | = sqrt(1^2 + (sqrt3)^2) = 2`
| `tan theta` | `= frac{sqrt3}{1} = sqrt3` |
| `theta` | `= frac{pi}{3}` |
| `text{arg} (beta)` | `= -frac{pi}{3}` |
`therefore \ beta = 2 \ text{cis} (-frac{pi}{3})`
| ii. | `beta^5` | `= 2^5 \ text{cis} (-frac{pi}{3} xx5)` |
| `= 32 \ text{cis} (-frac{5pi}{3} + 2 pi)` | ||
| `= 32 \ text{cis} (frac{pi}{3})` |
| iii. | `beta^5` | `= 32 ( cos (frac{pi}{3}) + i sin (frac{pi}{3}) )` |
| `= 32 ( frac{1}{2} + i frac{sqrt3}{2})` | ||
| `= 16 + i 16 sqrt3` |
--- 2 WORK AREA LINES (style=lined) ---
--- 8 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
| i. | `frac{1 + i sqrt3}{1 + i} xx frac{1 – i}{1 – i}` | `= frac{(1 + i sqrt3)(1 – i)}{1 – i^2}` |
| `= frac{1 – i + i sqrt3 – sqrt3 i^2}{2}` | ||
| `= frac{1 + sqrt3}{2} – i ( frac{1 – sqrt3}{2} )` |
ii. `z_1 = 1 + i sqrt3`
`| z_1 | = sqrt(1 + ( sqrt3)^2) = 2`
`text{arg} (z_1) = tan^-1 (sqrt3) = frac{pi}{3}`
`z_1 = 2 (cos frac{pi}{3} + i sin frac{pi}{3})`
`z_2 = 1 + i`
`| z_2 | = sqrt(1^2 + 1^2) = sqrt2`
`text{arg} (z_2) = tan^-1 (1) = frac{pi}{4}`
`z_2 = sqrt2 (cos frac{pi}{4} + i sin frac{pi}{4})`
| `frac{1 + i sqrt3}{1 + i}` | `= frac{z_1}{z_2}` |
| `= frac{2}{sqrt2} ( cos ( frac{pi}{3} – frac{pi}{4} ) + i sin ( frac{pi}{3} – frac{pi}{4} ) )` | |
| `= sqrt2 ( cos (frac{pi}{12}) + i sin (frac{pi}{12}) )` |
iii. `text{Equating real parts of i and ii:}`
| `sqrt2 cos (frac{pi}{12})` | `= frac{1 + sqrt3}{2}` |
| `cos(frac{pi}{12})` | `= frac{1 + sqrt3}{2 sqrt2} xx frac{sqrt2}{sqrt2}` |
| `= frac{sqrt2 + sqrt6}{4}` |
| iv. | `(frac{1 + i sqrt2}{1 + i})^12` | `= (sqrt2)^12 (cos (frac{pi}{12} xx 12) + i sin (frac{pi}{12} xx 12))` |
| `= 64 (cos pi + i sin pi)` | ||
| `= – 64` |
Express the complex number \(z=-2 \sqrt{2}-2 \sqrt{6} i\) in the exponential form. (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
\(4 \sqrt{2} e^{-i \small{\dfrac{2 \pi}{3}}}\)
| \(\abs{z}\) | \(=\sqrt{(2 \sqrt{2})^2+(2 \sqrt{6})^2}\) |
| \(=\sqrt{8+24}\) | |
| \(=4 \sqrt{2}\) |
| \(\tan \theta\) | \(=\dfrac{2 \sqrt{2}}{2 \sqrt{6}}=\dfrac{1}{\sqrt{3}}\) |
| \(\theta\) | \(=\dfrac{\pi}{6}\) |
\(\operatorname{Arg}(z)=-\left(\dfrac{\pi}{2}+\dfrac{\pi}{6}\right)=-\dfrac{2 \pi}{3}\)
| \(\therefore z\) | \(=4 \sqrt{2} \operatorname{cis}\left(\dfrac{-2 \pi}{3}\right)\) |
| \(=4 \sqrt{2} e^{-i \small{\dfrac{2 \pi}{3}}}\) |
The point `C` divides the interval `AB` so that `frac{CB}{AC} = frac{m}{n}`. The position vectors of `A` and `B` are `underset~a` and `underset~b` respectively, as shown in the diagram.
--- 6 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
Let `OPQR` be a parallelogram with `overset->(OP) = underset~p` and `overset->(OR) = underset~r`. The point `S` is the midpoint of `QR` and `T` is the intersection of `PR` and `OS`, as shown in the diagram.
--- 8 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
i.
| `frac{overset->(AC)}{overset->(AB)}` | `= frac{n}{m + n}` |
| `overset->(AC)` | `= frac{n}{m + n} * overset->(AB)` |
| `= frac{n}{m + n} (underset~b – underset~a)` |
| ii. | `overset->(OC)` | `= overset->(OA) + overset->(AC)` |
| `= underset~a + frac{n}{m + n} (underset~b – underset~a)` | ||
| `= underset~a – frac{n}{m + n} underset~a + frac{n}{m + n} underset~b` | ||
| `= (1 – frac{n}{m + n}) underset~a + frac{n}{m + n} underset~b` | ||
| `= (frac{m + n – n}{m + n}) underset~a + frac{n}{m + n} underset~b` | ||
| `= frac{m}{m + n} underset~a + frac{n}{m + n} underset~b` |
iii. `text{Show} \ \ overset->(OT) = frac{2}{3} underset~r + frac{1}{3} underset~p`
`text{Consider} \ \ Delta PTO \ \ text{and} \ \ Delta RTS:`
`angle PTO = angle RTS \ (text{vertically opposite})`
`angle OPT = angle SRT \ (text{vertically opposite})`
`therefore \ Delta PTO \ text{|||} \ Delta RTS\ \ text{(equiangular)}`
`OT : TS = OP : SR = 2 : 1`
`(text{corresponding sides in the same ratio})`
| `frac{overset->(OT)}{overset->(OS)}` | `= frac{2}{3}` |
| `overset->(OT)` | `= frac{2}{3} overset->(OS)` |
| `= frac{2}{3} ( underset~r + frac{1}{2} underset~p)` | |
| `= frac{2}{3} underset~r + frac{1}{3} underset~p` |
iv. `text{Let} \ \ overset->(OT) \ text{divide} \ PR\ text{so that}\ \ frac{TR}{PT} = frac{m}{n}`
`text{Using part (ii):}`
| `overset->(OT)` | `= frac{m}{m + n} underset~p + frac{n}{m + n} c` |
| `overset->(OT)` | `= frac{1}{3} underset~p + frac{2}{3} underset~r \ \ \ (text{part (iii)})` |
| `frac{m}{m + n}` | `= frac{1}{3} , frac{n}{m + n} = frac{2}{3}` |
`=> \ m = 1 \ , \ n = 2`
`therefore \ T \ text{divides} \ PR \ text{in ratio 2 : 1}.`
In the set of integers, let `P` be the proposition:
'If `k + 1` is divisible by 3, then `k^3 + 1` divisible by 3.'
--- 5 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 8 WORK AREA LINES (style=lined) ---
i. `text{Let} \ \ k + 1 = 3N, \ N∈ Z`
`=> k = 3N – 1`
| `k^3 + 1` | `= (3N -1)^3 + 1` |
| `= (3N)^3 + 3(3N)^2 (-1) + 3(3N)(-1)^2 + (-1)^3 + 1` | |
| `= 27N^3 – 27N^2 + 9N – 1 + 1` | |
| `= 3 (9N^3 – 9N^2 + 3N)` | |
| `= 3Q \ , \ Q ∈ Z` |
`therefore \ text{If} \ \ k+ 1 \ \ text{is divisible by 3}, text{then} \ \ k^3 + 1 \ \ text{is divisible by 3.}`
ii. `text{Contrapositive}`
`text{If} \ \ k^3 + 1 \ \ text{is not divisible by 3, then}\ \ k + 1\ \ text{is not divisible by 3.}`
iii. `text{Converse:}`
`text{If} \ \ k^3 + 1\ \ text{is divisible by 3, then}\ \ k + 1\ \ text{is divisible by 3.}`
`text(Contrapositive of converse:)`
`text{If}\ \ k + 1\ \ text{is not divisible by 3, then}\ \ k^3 + 1\ \ text{is not divisible by 3.}`
`text(i.e.)\ \ k + 1 \ \ text{is not divisible by 3 when}\ \ k + 1 = 3Q + 1\ \ text{or}\ \ k + 1 = 3Q + 2, text{where}\ Q ∈ Z`
| `text{If} \ \ k + 1` | `= 3Q + 1\ \ => \ k=3Q` |
| `k^3 + 1` | `= (3Q)^3 + 1` |
| `= 27Q^3 + 1` | |
| `= 3(9Q^3) + 1` | |
| `= 3M + 1 \ \ (text{not divisible by 3,}\ M ∈ Z)` |
| `text{If} \ \ k + 1` | `= 3Q + 2\ \ => \ k=3Q+1` |
| `k^3 + 1` | `= (3Q + 1)^3 + 1` |
| `= (3Q)^3 + 3(3Q)^2 + 3(3Q) + 1 + 1` | |
| `= 27Q^3 + 27Q^2 + 9Q + 2` | |
| `= 3(9Q^3 + 9Q^2 + 3Q) + 2` | |
| `= 3M + 2 \ (text{not divisible by 3,}\ M ∈ Z) ` |
`therefore \ text{By contrapositive, if}\ \ k^3 + 1\ \ text {is divisible by 3, k + 1 is divisible by 3.}`
Let `z_1` be a complex number and let `z_2 = e^(frac{i pi}{3}) z_1`
The diagram shows points `A` and `B` which represent `z_1` and `z_2`, respectively, in the Argand plane.
--- 6 WORK AREA LINES (style=lined) ---
--- 8 WORK AREA LINES (style=lined) ---
i.
| `text{Let}` | `z_1` | `= r(cos theta + i sin theta)` |
| `z_2` | `= e^(i frac{pi}{3}) z_1` | |
| `= r (cos ( theta + frac{pi}{3} ) + i sin (theta + frac{pi}{3}))` |
`| z_1 | = | z_2 | => OA = OB`
` angle AOB = frac{pi}{3} \ ( z_2 \ text{is a} \ frac{pi}{3} \ text{anti-clockwise rotation of} \ z_1 )`
`=> angle OBA = angle BAO = pi/3\ \ \ text{(angles opposite equal sides)}`
`therefore \ OAB \ text{is equilateral}`
| ii. | `z_1` | `= z_2 e^(i frac{pi}{3})` |
| `frac{z_1}{z_2}` | `= e^(i frac{pi}{3})` | |
| `(frac{z_1}{z_2})^3` | `= e^((3 xx i frac{pi}{3})) \ \ (text{by De Moivre})` | |
| `frac{z_1^3}{z_2^3}` | `= e^(i pi)` | |
| `z_1^3` | `= -z_2^3` | |
| `z_1^3 + z_2^3` | `= 0` |
| `(z_1 + z_2)(z_1^2 – z_1 z_2 + z_2^2)` | `= 0` |
| `z_1^2 – z_1 z_2 + z_2^2` | `= 0` |
| `z_1^2 + z_2^2` | `= z_1 z_2` |
--- 2 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
| i. | `e^(i n theta) + e^(-i n theta)` | `= cos(n theta) + i sin(n theta) + cos(-n theta) + i sin(-n theta)` |
| `= cos(n theta) + i sin(n theta) + cos(n theta) – i sin(n theta)` | ||
| `= 2 cos (n theta)` |
| ii. | `(e^{i theta} + e^{-i theta})^4` | `= (2 cos theta)^4` |
| `= 16 cos^4 theta` |
`text{Expand} \ (e^{i theta} + e^{-i theta})^4 :`
`e^(i 4 theta) + 4 e^(i 3 theta) e^(-i theta) + 6 e^(i 2 theta) e^(-i 2 theta) + 4 e^(i theta) e^(-i 3 theta) + e^(-i 4 theta)`
`= e^(i 4 theta) + 4e^(i 2 theta) + 6 + 4^(-i 2 theta) + e^(-i 4 theta)`
`= e^(i 4 theta) + e^(i 4 theta) + 4 (e^{i 2 theta} + e^{-i 2 theta}) + 6`
`= 2 cos (4 theta) + 8 cos (2 theta) + 6`
| `therefore \ 16 cos^4 theta` | `= 2 cos (4 theta) + 8 cos (2 theta) + 6` |
| `cos^4 theta` | `= frac{1}{8} cos(4 theta) + 1/2 cos(2 theta) + 3/8` |
| `cos^4 theta` | `= frac{1}{8} (cos(4 theta) + 4 cos(2 theta) + 3)` |
| iii. | `int_0^(frac{pi}{2}) cos^4 theta\ d theta` | `= frac{1}{8} int_0^(frac{pi}{2}) cos(4 theta) + 4 cos(2 theta) + 3\ d theta` |
| `= frac{1}{8} [ frac{1}{4} sin(4 theta) + 2 sin (2 theta) + 3 theta ]_0^(frac{pi}{2}` | ||
| `= frac{1}{8} [( frac{1}{4} sin (2 pi) + 2 sin pi + frac{3 pi}{2}) – 0 ]` | ||
| `= frac{1}{8} ( frac{3 pi}{2})` | ||
| `= frac{3 pi}{16}` |
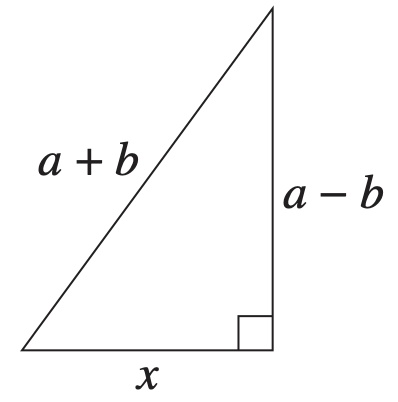
--- 5 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
i. `text{Strategy 1}`
`text{Using Pythagoras:}`
| `x` | `= sqrt{(a + b)^2-(a-b)^2}` |
| `= sqrt(4ab)` | |
| `= 2 sqrt(ab)` |
`a + b \ text{is a hypotenuse}`
| `a + b` | `≥ x` |
| `a + b` | `≥ 2sqrt(ab)` |
| `frac{a + b}{2}` | `≥ sqrt(ab)` |
`text{Strategy 2}`
| `(sqrta-sqrtb)^2` | `≥ 0` |
| `a-2 sqrt(a) sqrt(b) + b` | `≥ 0` |
| `a + b` | `≥ 2 sqrt(ab)` |
| `frac{a + b}{2}` | `≥ sqrt(ab)` |
ii. `text{Let} \ \ a = p , b = 2 q`
`text(Using part i:)`
| `frac{p + 2q}{2}` | `≥ sqrt(2 pq)` |
| `p + 2q` | `≥ 2 sqrt(2 pq)` |
| `p^2 + 4pq + 4 q^2` | `≥ 8 pq` |
| `p^2 + 4 q^2` | `≥ 4 pq` |
Consider the two lines in three dimensions given by
`underset~r = ((3),(-1),(7)) + λ_1 ((1),(2),(1))` and `underset~r = ((3),(-6),(2)) + λ_2 ((-2),(1),(3))`.
By equating components, find the point of intersection of the two lines. (3 marks)
--- 8 WORK AREA LINES (style=lined) ---
`((1),(-5),(5))`
`underset~(r_1) = ((3),(-1),(7)) + λ_1 ((1),(2),(1)) = ((3 + λ_1),(-1 + 2λ_1),(7 + λ_1))`
`underset~(r_2) = ((3),(-6),(2)) + λ_2 ((-2),(1),(3)) = ((3 – 2λ_2),(-6 + λ_2),(2 + 3λ_2))`
`text{Intersection occurs when:}`
| `3 + λ_1 ` | `= 3 – 2λ_2 \ … \ (1)` |
| `-1 + 2λ_1` | `= -6 + λ_2 \ … \ (2)` |
| `7 + λ_1` | `= 2 + 3λ_2 \ … \ (3)` |
`text{Subtract} \ (3) – (1):`
| `4` | `= -1 + 5 λ_2` |
| `λ_2` | `=1` |
`text{Substitute} \ \ λ_2 = 1\ \ text{into} \ (1):`
| `3 + λ_1` | `= 1` |
| `λ_1` | `= -2` |
`text{Test that}\ \ λ_1 = -2 \ , \ λ_2 = 1\ \ text{satisfies} \ (2):`
| `-1 + 2 xx – 2` | `= -6 + 1` |
| `-5` | `= -5` |
`∃ \ λ_1, λ_2, \ text{that satisfy all equations}`
`=> \ text{3 lines intersect at a point}`
`:.\ text{Point of intersection}`
`= ((3),(-6),(2)) + 1 ((-2),(1),(3)) = ((1),(-5),(5))`
A particle is projected from the origin with initial velocity `u` m/s at an angle `theta` to the horizontal. The particle lands at `x = R` on the `x`-axis. The acceleration vector is given by `underset~a = ((0),(-g))`, where `g` is the acceleration due to gravity. (Do NOT prove this.)
--- 8 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
--- 7 WORK AREA LINES (style=lined) ---
i. `underset~a = ((0),(-g))`
`ddotx = 0`
`dotx = int ddotx \ dt = c`
`text{When} \ \ t = 0, \ dotx = u cos theta \ => \ c = u cos theta`
`=> dotx = u cos theta`
`x = int dotx \ dt =u t cos theta + c`
`text{When} \ \ t = 0 , \ x = 0, \ c = 0`
`therefore \ x = ut cos theta`
`ddoty = -g`
`doty = int-g \ dt = -g t + c`
`text{When} \ \ t = 0 , \ doty = u sin theta`
`=> doty = u sin theta-g t`
`y = int doty \ dt = ut sin theta-frac {1}{2} g t^2 + c`
`text{When} \ \ t = 0, \ y = 0 \ => \ c = 0`
`therefore y = ut sin theta-frac(1)(2) g t^2`
`:. underset~r = ((x),(y)) = ((ut cos theta),(ut sin theta-frac{1}{2} g t^2))`
ii. `x = ut \ cos theta`
`t = frac{x}{u \ cos theta}`
`text{Substitute into} \ y:`
| `y` | `= u * frac{x}{u \ cos theta}\ sin theta-frac{1}{2} g ( frac{x}{u \ cos theta} )^2` |
| `= x tan theta-frac{gx^2}{2 u^2 cos^2 theta}` | |
| `= frac{-gx^2}{2u^2} ( frac{1}{cos^2 theta}-frac{2u^2}{gx} tan theta )` | |
| `= frac{-gx^2}{2u^2} ( sec^2 theta-frac{2u^2}{gx} tan theta )` | |
| `= frac{-gx^2}{2u^2} ( tan^2 theta-frac{2u^2}{gx} tan theta + 1 )` |
iii. `text{When} \ \ x = R \ , \ y = 0`
| `frac{-gR^2}{2 u^2}` | `( tan^2 theta-frac{2u^2}{gR} tan theta + 1 ) = 0` |
| `tan^2 theta-frac{2u^2}{gR} tan theta + 1 = 0` | |
| `Delta` |
`= ( frac{-2u^2}{gR} )^2-4 * 1 * 1` |
| `= frac{4u^4}{g^2 R^2}-4` |
| `u^2` | `> gR\ \ \ text{(given)}` | |
| `u^4` | `> g^2 R^2` | |
| `frac{u^4}{g^2 R^2}` | `> 1` | |
| `frac{4u^4}{g^2 R^2}` | `> 4` | |
| `frac{4u^4}{g^2 R^2}-4` | `> 0` | |
| `Delta` | `> 0` |
`therefore \ 2 \ text{distinct values of} \ \ theta\ \ text{satisfy} \ \ x = R.`
A 50-kilogram box is initially at rest. The box is pulled along the ground with a force of 200 newtons at an angle of 30° to the horizontal. The box experiences a resistive force of `0.3R` newtons, where `R` is the normal force, as shown in the diagram.
Take the acceleration `g` due to gravity to be 10m/s2.
--- 5 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
i.
`text{Resolving forces vertically:}`
| `R + 200 \ sin 30^@` | `= 50g` |
| `R + 200 xx frac{1}{2}` | `= 50 xx 10` |
| `R + 100` | `= 500` |
| `therefore \ R` | `= 400 \ text(N)` |
ii. `text{Resolving forces horizontally:}`
| `text{Net Force}` | `= 200 \ cos 30^@ – 0.3 R` |
| `= 200 xx frac{sqrt3}{2} – 0.3 xx 400` | |
| `= 100 sqrt3 – 120` | |
| `= 53.2 \ text{N (to 1 d. p.)}` |
| iii. | `F` | `=ma` |
| `50 a` | `=100 sqrt300 – 120` | |
| `a` | `= frac{100 sqrt3 – 120}{50}\ text(ms)^(-2)` |
`text{Initially} \ \ u = 0,`
| `v` | `= u + at` |
| `v_(t=3)` | `= 0 + frac{100 sqrt3 – 120}{50} xx 3` |
| `= 3.1923 \ …` | |
| `= 3.19 \ text{ms}^-1 \ text{(to 2 d.p.)}` |
Solve `z^2 + 3 z + (3-i) = 0`, giving your answer(s) in the form `a + bi`, where `a` and `b` are real. (4 marks)
--- 10 WORK AREA LINES (style=lined) ---
`z= -1 + i \ \ text{or} \ \ -2-i`
`z^2 + 3z + (3-i) = 0`
| `z` | `= frac{-3 ± sqrt(9-4 · 1 (3-i))}{2}` |
| `= frac{-3 ± sqrt(4i-3)}{2} ` |
`text{Consider} \ \ Delta = sqrt(4i-3) :`
| `x + i y` | `= sqrt(4i-3)` |
| `(x + iy)^2` | `= 4i-3` |
| `x^2-y^2 + 2xyi` | `= 4i-3` |
`text{Equating real and imaginary parts:}`
| `2 xy` | `= 4` |
| `xy` | `= 2\ …\ (1)` |
| `x^2-y^2` | `= -3\ …\ (2)` |
`=> x = 1 \ , \ y =2`
`=> \ x + iy = 1 + 2 i`
| `therefore z` | `= frac{-3 ± (1 + 2i)}{2}` |
| `z ` | `= -1 + i \ \ text{or} \ \ -2-i` |
Consider the two vectors `underset~u = 2 underset~i - underset~j + 3 underset~k` and `underset~v = p underset~i + underset~j + 2 underset~k`.
For what values of `p` are `underset~u - underset~v` and `underset~u + underset~v` perpendicular? (3 marks)
--- 8 WORK AREA LINES (style=lined) ---
`p= ± 3`
`underset~u – underset~v = ((-2),(-1),(3)) – ((p),(1),(2)) = ((-2 – p),(-2),(1))`
`underset~u + underset~v = ((-2),(-1),(3)) + ((p),(1),(2)) = ((p – 2),(0),(5))`
`⊥ \ text{when} \ \ (underset~u – underset~v) · (underset~u + underset~v ) = 0 :`
`((-2 – p),(-2),(1)) · ((p – 2),(0),(5)) = 0`
| `-(p + 2)(p-2) + 5` | `= 0` |
| `-(p^2 – 4) + 5` | `= 0` |
| `-p^2 + 9` | `= 0` |
| `p^2` | `= 9` |
| `p` | `= ± 3` |
A particle starts at the origin with velocity 1 and acceleration given by
`a = v^2 + v`,
where `v` is the velocity of the particle.
Find an expression for `x`, the displacement of the particle, in terms of `v`. (3 marks)
--- 7 WORK AREA LINES (style=lined) ---
`x= ln \ | frac{v + 1}{2} |`
| `a` | `= v^2 + v` |
| `v · frac{dv}{dx}` | `= v^2 + v` |
| `frac{dv}{dx}` | `= v + 1` |
| `frac{dx}{dv}` | `= frac{1}{v + 1}` |
| `x` | `= int frac{1}{v + 1}\ dv` |
| `= ln \ | v + 1 | + c` |
`text{When} \ \ x = 0 , \ v = 1`
`0 = ln \ 2 + c`
`c = -ln \ 2`
| `therefore \ x` | `= ln \ | v + 1| – ln \ 2` |
| `= ln \ | frac{v + 1}{2} |` |
Use integration by parts to evaluate `int_1^e x ln x \ dx`. (3 marks)
`frac{e^2 + 1}{4}`
| `u = ln \ x` | `v′ = x` |
| `u′ = frac{1}{x}` | `v = frac{x^2}{2}` |
| `int _1^e x \ ln \ x \ dx` | `= [ frac{x^2}{2} · ln \ x ]_1^e – int_1^e frac{x^2}{2} · frac{1}{x}\ dx` |
| `= [frac{e^2}{2} ln \ e – frac{1}{2} ln 1]- int_1^e frac{x}{2}\ dx` | |
| `= frac{e^2}{2} – [ frac{x^2}{4}]_1^e` | |
| `= frac{e^2}{2} – ( frac{e^2}{4} – frac{1}{4} )` | |
| `= frac{e^2 + 1}{4}` |
Consider the proposition:
'If `2^n - 1` is not prime, then `n` is not prime'.
Given that each of the following statements is true, which statement disproves the proposition?
`D`
`text(Strategy 1 – Contradiction)`
`text(Consider option)\ D,`
`text(S)text(ince)\ \ 2^11 -1\ \ text(is divisible by 23, it is NOT prime.)`
`text(The proposition states that 11 is not prime which is false.)`
`:. 2^11 – 1\ \ text(is divisible by 23, disproves the proposition.)`
`text(Strategy 2 – Contrapositive)`
`text{The proposition is conditional}`
`X => Y`
`text{L}text{ogically equivalent contrapositive statement}`
`not \ Y => not \ X`
`text{i.e. If} \ n \ text{is prime} \ => \ 2^n – 1 \ text{is prime.}`
`text{Consider D:}`
`n = 11 \ text{(prime)}`
`2^11 – 1 \ text{is divisible by 23 (not prime)}`
`therefore \ text{Contrapositive statement is false and disproves the proposition.}`
`=> \ D`