SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Complex Numbers, SPEC1 2019 VCAA 7

  1. Show that  `3-sqrt3 i = 2sqrt3 text(cis)(-pi/6)`.   (1 mark)

  2. Find  `(3-sqrt3 i)^3`, expressing your answer in the form  `x + iy`, where  `x`,  `y ∈ R`.   (2 marks)

  3. Find the integer values of  `n`  for which  `(3-sqrt3 i)^n`  is real.   (1 mark)

  4. Find the integer values of  `n`  for which  `(3-sqrt3 i)^n = ai`, where  `a`  is a real number.   (1 mark)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `0-i 24sqrt3`
  3. `n = 6k\ \ (k ∈ ZZ)`
  4. `n = 3 + 6k\ \ (k ∈ ZZ)`
Show Worked Solution

a.  `|3-sqrt3 i|= sqrt(3^2 + (-sqrt3)^2)= sqrt12= 2sqrt3`

`text(Arg)(3-sqrt3 i)` `= tan^(-1)(-(sqrt3)/3)= -pi/6`
   

`:. 3-sqrt3 i = 2sqrt3\ text(cis)(-pi/6)`

b.    `(3-sqrt3 i)^3` `= (2sqrt3)^3\ text(cis)(3 xx-pi/6)`
    `= 24sqrt3\ text(cis)(-pi/2)`
    `= 24sqrt3(cos(-pi/2) + isin(-pi/2))`
    `= 0-i 24sqrt3`

 

c.   `(3-sqrt3 i)^n = (2sqrt3)^n\ text(cis)((-npi)/6)`

`text(Real when)\ \ sin(-(npi)/6) = -sin((npi)/6) = 0`

`(npi)/6 = 0, pi, 2pi, …, kpi\ \ (k ∈ ZZ)`

`:. n = 6k\ \ (k ∈ ZZ)`

 

d.  `(3-sqrt3 i)^n = ai\ \ text(when)\ \ cos(-(npi)/6) = cos((npi)/6) = 0`

`(npi)/6 = pi/2, (3pi)/2, …, pi/2 + kpi\ \ (k ∈ ZZ)`

`:. n = 3 + 6k\ \ (k ∈ ZZ)`

Calculus, SPEC1 2019 VCAA 5

The graph of  `f(x) = cos^2(x) + cos(x) + 1`  over the domain  `0 <= x <= 2pi`  is shown below.

  1.  i.  Find `f^{′}(x)`.  (1 mark)

  2. ii. Hence, find the coordinates of the turning points of the graph in the interval  `(0, 2pi)`.  (2 marks)

  3. Sketch the graph of  `y = 1/(f(x))`  on the set of axes above. Clearly label the turning points and endpoints of this graph with their coordinates.  (3 marks)
Show Answers Only
  1. i.  `−sin(x)(2cos(x) + 1)`
  2. ii. `(pi, 1), ((2pi)/3,3/4), ((4pi)/3, 3/4)`
  3.  

Show Worked Solution
a.i.    `f(x)` `= cos^2(x) + cos(x) + 1`
  `f^{′}(x)` `= -2sin(x)cos(x)-sin(x)`
    `= -sin(x)(2cos(x) + 1)`

 

a.ii.   `text(SP when)\ \ sin(x) = 0\ \ text(or)\ \ 2cos(x) + 1 = 0`

`sin(x) = 0 \ => \ x = pi\ \ (x = 0\ \ text{not in domain})`

`2cos(x) + 1` `= 0`
`cos(x)` `= -1/2`
`x` `= (2pi)/3, (4pi)/3`

 
`text(When)\ \ cos(x) = −1/2 \ => \ f(x) = 1/4-1/2 + 1 = 3/4`

`:.\ text(Turning Points:)\ (pi, 1), ((2pi)/3,3/4), ((4pi)/3, 3/4)`

 

b.   

Calculus, MET2 2019 VCAA 1

Let  `f: R -> R,\ \ f(x) = x^2e^(-x^2)`.

  1. Find `f^{\prime}(x)`.  (1 mark)

  2. i.  State the nature of the stationary point on the graph of  `f`  at the origin.  (1 mark)

  3. ii.  Find the maximum value of the function  `f`  and the values of  `x`  for which the maximum occurs.  (2 marks)

  4. iii. Find the values of  `d in R`  for which  `f(x) + d`  is always negative.  (1 mark)

  5. i.  Find the equation of the tangent to the graph of  `f`  at  `x = –1`.  (1 mark)

  6. ii. Find the area enclosed by the graph of  `f`  and the tangent to the graph of  `f`  at  `x = –1`, correct to four decimal places.  (2 marks)

  7. Let  `M(m, n)`  be a point on the graph of  `f`, where  `m in [0, 1]`.
  8. Find the minimum distance between  `M`  and the point  `(0, e)`, and the value of  `m`  for which this occurs, correct to three decimal places.  (3 marks)

Show Answers Only

  1. `2x e^(-x^2)(1-x^2)`
  2. i.  `text(Local minimum)`
  3. ii. `f(x)_max= 1/e\ \ text(when) \ x = -1 and 1`
  4. iii. `d<1/e`
  5. i.  `y = 1/e` 
  6. ii. `0.3568\ text{(to 4 d.p.)}`
  7. `D_(min) = 2.511\ \ text(when)\ \ m ~~ 0.783`

Show Worked Solution

a.    `f^{\prime}(x)` `= x^2 ⋅ -2x ⋅ e^(-x^2) + e^(-x^2) ⋅ 2x`
    `= 2x e^(-x^2) (1-x^2)`

​

b.i.    `f ^{″}(0) = 2 > 0\ \ \ text{(by CAS)}`
  `:.\ text(Local minimum)`

 

b.ii.    `text(SP’s occur when)\ \ x = –1, 0, 1`
  `f(x)_max = 1/e\ \ text(when)\ \ x = –1  and  1`

 

b.iii.    `f(x)_max + d` `< 0`
  `d` `< 1/e`

 

c.i.    `text(At)\ \ x = –1, \ f(x)\ text(has a max turning point).`
  `:.\ text(T)text(angent:)\ \ y = 1/e`

 

c.ii.    `text(Area)` `= int_(_1)^1 1/e-x^2e^(-x^2) dx`
    `~~ 0.3568\ text{(to 4 d.p.)}`

 

d.   `text(When)\ x = m,\ \ n = m^2 e^(-m^2)`

`text(Find distance between)\ \ M(m, m^2 e^(-m^2)) and P(0, e):`

`D = sqrt((m-0)^2 + (m^2 e^(-m^2)-e)^2)`

`=>\ text(MIN distance when)\ \ (dD)/(dm) = 0`

`D_(min) = 2.511\ \ text(when)\ \ m ~~ 0.783\ \ \ text{(by CAS)}`

Statistics, SPEC1 2019 VCAA 3

A machine produces chocolate in the form of a continuous cylinder of radius 0.5 cm. Smaller cylindrical pieces are cut parallel to its end, as shown in the diagram below.

The lengths of the pieces vary with a mean of 3 cm and a standard deviation of 0.1 cm.
 


 

  1. Find the expected volume of a piece of chocolate in cm³.   (1 mark)

  2. Find the variance of the volume of a piece of chocolate in cm6.   (1 mark)

  3. Find the expected surface area of a piece of chocolate in cm².   (1 mark)

Show Answers Only
  1. `0.75pi\ text(cm³)`
  2. `0.000625pi^2\ text(cm)^6`
  3. `3.5pi\ text(cm²)`
Show Worked Solution
a.    `E(V)` `= pir^2 xx E(h)`
    `= pi xx 0.5^2 xx 3`
    `= 0.75pi\ text(cm³)`

 

b.    `text(Var)(V)` `= text(Var)(pir^2h)`
    `= pi^2 xx 0.5^4 xx text(Var)(h)`
    `= 0.0625pi^2 xx 0.1^2`
    `= 0.000625pi^2\ text(cm)^6`

 

c.    `E text{(Surface Area)}` `= 2pir^2 + 2pir xx E(h)`
    `= 2pir(r +E(h))`
    `= pi(0.5 + 3)`
    `= 3.5pi\ text(cm²)`

Functions, 2ADV F2 SM-Bank 35

  1. Sketch the function  `y = f(x)`  where  `f(x) = (x - 1)^3`  on a number plane, labelling all intercepts.  (1 mark)

  2. On the same graph, sketch  `y = −f(−x)`. Label all intercepts.  (2 marks)

Show Answers Only
  1.   
  2.   
Show Worked Solution

i.   `y = (x – 1)^3 => y = x^3\ text(shifted 1 unit to the right.)`
 

 

ii.   `y = −f(x) \ => \ text(reflect)\ \ y = (x – 1)^3\ \ text(in)\ xtext(-axis).`

`y = −f(−x) \ => \ text(reflect)\ \ y = −f(x)\ \ text(in)\ ytext(-axis).`

 

Functions, 2ADV F1 SM-Bank 37

Find all values of  `x`  for which  `|\ x - 4\ | = x/2 + 7`.  (3 marks)

Show Answers Only

`x = 22\ \ text(or)\ −2`

Show Worked Solution
`x – 4` `= x/2 + 7` `text(or)` `-(x-4)` `= x/2 + 7`
`2x – 8` `= x + 14`   `−2x + 8` `= x + 14`
`x` `= 22`   `3x` `= −6`
      `x` `= −2`

`:. x = 22\ \ text(or)\ −2`

Functions, 2ADV F1 SM-Bank 36

Consider the function  `f(x) = 1/(x + 2)`.
 

 
 

  1. Sketch the graph  `y = f(−x)`.   (2 marks)

  2. On the same graph, sketch  `y = −f(x)`.   (2 marks)

Show Answers Only

i.

ii.   

Show Worked Solution

i.   `text(Sketch)\ \ y = 1/(x + 2)`

`y = f(−x) \ =>\ text(reflect)\ \ y = 1/(x + 2)\ \ text(in the)\ ytext(-axis).`
 

 

ii.   `y = −f(x) \ =>\ text(reflect)\ \ y = 1/(x + 2)\ \ text(in the)\ xtext(-axis).`
 

Probability, MET2 2019 VCAA 7 MC

The discrete random variable `X` has the following probability distribution.
 

  `qquad x` `qquad 0 qquad` `qquad 1 qquad` `qquad 2 qquad` `qquad 3 qquad`
  `qquad Pr(X = x) qquad` `a` `3a` `5a` `7a`

 
The mean of `X` is

  1. `1/16`
  2. `1`
  3. `35/16`
  4. `17/8`
  5. `2`
Show Answers Only

`D`

Show Worked Solution

`16a = 1 qquad => qquad a = 1/16`

`text(E)(X)` `= 3/16 xx 1 + 5/16 xx 2 + 7/16 xx 3`
  `=34/16`
  `= 17/8`

 
`=>   D`

Calculus, MET2 2019 VCAA 5 MC

Let  `f prime(x) = 3x^2 - 2x`  such that  `f(4) = 0`.

The rule of  `f`  is

A.   `f(x) = x^3 - x^2`

B.   `f(x) = x^3 - x^2 + 48`

C.   `f(x) = x^3 - x^2 - 48`

D.   `f(x) = 6x - 2`

E.   `f(x) = 6x - 24`

Show Answers Only

`C`

Show Worked Solution
`f(x)` `= int 3x^2 – 2x\ dx`
  `= x^3 – x^2 + c`

 

`text(When)\ \ x = 4, \ f(x) = 0`

`0 = 4^3 – 4^2 + c`

`c = -48`
 

`:. f(x) = x^3 – x^2 – 48`

`=>   C`

Statistics, 2ADV S2 SM-Bank 14

A probability density function  `f(x)`  is given by
 

`f(x) = {(px(3 - x), \ text(if)\ \ 0 <= x <= 3),(0, \ text(if)\ \ x < 0\ \ text(or if)\ \ x > 3):}`
 

where  `p`  is a positive constant.

  1. Find the value of  `p`.  (2 marks)

  2. Find the mode of  `f(x)`.  (2 marks)

Show Answers Only
  1. `2/9`
  2. `3/2`
Show Worked Solution

i.   `text(Total Area under curve = 1)`

`p int_0^3 3x-x^2\ dx` `= 1`
`p[3/2 x^2-(x^3)/3]_0^3` `= 1`
`p[27/2-27/3-0]` `= 1`
`(9p)/2` `= 1`
`p` `= 2/9`

 

ii.   `f(x) = 2/9(3x-x^2)`

`f^{′}(x) = 2/9(3-2x)`

`text(S.P. when)\ \ f^{′}(x) = 0:`

`3-2x` `= 0`
`x` `= 3/2`

 
`f^{″}(x) = -4/9 < 0 \ =>\ text(MAX)`

`:.\ text(Mode) = 3/2`

Statistics, 2ADV S3 EQ-Bank 17

The diastolic measurement for blood pressure in 35-year-old people is normally distributed, with a mean of 75 and a standard deviation of 12.

  1. A person is considered to have low blood pressure if their diastolic measurement is 63 or less.What percentage of 35-year-olds have low blood pressure?  (1 mark)

  2. Calculate the `z`-score for a diastolic measurement of 57.  (1 mark)

  3. The probability that a 35-year-old person has a diastolic measurement for blood pressure between 57 and 63 can be found by evaluating
     
    `qquad qquad int_a^b f(x)\ dx`
     
    where `a` and `b` are constants and where
     
    `qquad qquad f(x) = 1/(sqrt(2pi)) e^((−x^2)/2)`
     
    is the normal probability density function with mean 0 and standard deviation 1.

     

    By first finding the values `a` and `b`, calculate an approximate value for this probability by using the trapezoidal rule with 3 function values.  (3 marks)

  4. Hence, find the approximate probability that a 35-year-old person chosen at random has a diastolic measurement of 57 or less.  (1 mark)

Show Answers Only
  1. `16text(% have low blood pressure)`
  2. `−1.5`
  3. `9.2text(%)`
  4. `6.8text(%)`
Show Worked Solution
i.    `ztext(-score)\ (63)` `= (x – mu)/σ`
    `= (63 – 75)/12`
    `= −1`

 

`:. 16text(% have low blood pressure)`

 

ii.    `ztext(-score)` `= (57 – 75)/12`
    `= −1.5`

 

iii.  `y = 1/sqrt(2pi) e^((−x^2)/2)`

 
`text(Area)` `= h/2(y_0 + 2y_1 + y_2)`
  `~~ 0.25/2 (0.1295 + 2 xx 0.1826 + 0.2420)`
  `~~ 0.0920`
  `~~ 9.2text(%)`

 

iv.   

 

`P(text{blood pressure}\ <= 57)` `= 16 – 9.2`
  `~~ 6.8text(%)`

Algebra, MET2 2019 VCAA 2 MC

The set of values of  `k`  for which  `x^2 + 2x-k = 0`  has two real solutions is

  1. `{-1, 1}`
  2. `(-1, oo)`
  3. `(-oo, -1)`
  4. `{-1}`
  5. `[-1, oo)`
Show Answers Only

`B`

Show Worked Solution

`text(Two real solutions):`

`b^2-4ac` `> 0`
`4-4 ⋅ 1 ⋅ (-k)` `> 0`
`4k` `> -4`
`k` `> -1`

 
`k in (-1, oo)`

`=>   B`

Graphs, MET2 2019 VCAA 1 MC

Let  `f: R -> R,\ \ f(x) = 3 sin ((2x)/5) - 2`.

The period and range of  `f`  are respectively

  1. `5 pi`  and  `[-3, 3]`
  2. `5 pi`  and  `[-5, 1]`
  3. `5 pi`  and  `[-1, 5]`
  4. `(5 pi)/2`  and  `[-5, 1]`
  5. `(5 pi)/2`  and  `[-3, 3]`
Show Answers Only

`B`

Show Worked Solution
`text(Period)` `= (2pi)/n`
  `= (2 pi)/(2/5)`
  `= 5 pi`
   
`text(Range)` `= [-2 -3, -2 + 3]`
  `= [-5, 1]`

 
`=>   B`

Calculus, MET1 2019 VCAA 7

The graph of the relation  `y = sqrt (1-x^2)`  is shown on the axes below. `P` is a point on the graph of this relation, `A` is the point `(-1, 0)` and `B` is the point `(x, 0)`.
 

  1. Find an expression for the length `PB` in terms of `x` only.   (1 mark) 

  2. Find the maximum area of the triangle `ABP`.  (3 marks)

Show Answers Only
  1. `PB = sqrt(1-x^2)`
  2. `(3 sqrt 3)/8`
Show Worked Solution

a.    `PB = sqrt(1-x^2)`

 

b.    `A` `= 1/2 ⋅ AB ⋅ PB`
    `= 1/2 (x + 1) ⋅ (1-x^2)^(1/2)`
  `(dA)/(dx)` `= 1/2[(x + 1) ⋅ 1/2 ⋅ -2x ⋅ 1/sqrt(1-x^2) + sqrt(1-x^2)]`
    `= 1/2((-x^2-x + 1-x^2)/sqrt(1-x^2))`
    `= (-2x^2-x + 1)/(2 sqrt(1-x^2))`

 
`text(Find max when)\ \ (dA)/(dx) = 0`

`2x^2 + x-1 = 0`

`(2x-1)(x + 1) = 0`

`x = 1/2 qquad (x =\ text{–1 is a min)}`

`:. A_max` `= 1/2 (3/2)(1-1/4)^(1/2)`
  `= 3/4 ⋅ sqrt(3/4)`
  `= (3 sqrt 3)/8`

Probability, MET1 2019 VCAA 6

Fred owns a company that produces thousands of pegs each day. He randomly selects 41 pegs that are produced on one day and finds eight faulty pegs.

  1. What is the proportion of faulty pegs in this sample?  (1 mark) 

  2. Pegs are packed each day in boxes. Each box holds 12 pegs. Let  `hat P`  be the random variable that represents the proportion of faulty pegs in a box.
  3. The actual proportion of faulty pegs produced by the company each day is `1/6`.
  4. Find  `text(Pr)(hat P < 1/6)`. Express your answer in the form  `a(b)^n`, where  `a`  and  `b`  are positive rational numbers and  `n`  is a positive integer.  (2 marks)

Show Answers Only

  1. `8/41`
  2. `(17/6) ⋅ (5/6)^11`

Show Worked Solution

a.    `text(Proportion of faulty pegs) = 8/41`
 

b.   `hat P = x/n = 1/6`

`text(Given)\ \ n = 12`

`1/6 = X/12 \ => \ X = 2`

`X\ ~\ text(Bi) (12, 1/6)`

`text(Pr)(hat P < 1/6)` `= text(Pr)(X < 2)`
  `= text(Pr)(X = 0) + text(Pr)(X = 1)`
  `= \ ^12 C_0 * (5/6)^12 + \ ^12 C_1 ⋅ (1/6)(5/6)^11`
  `= (5/6)^11 (5/6 + 12/6)`
  `= (17/6) ⋅ (5/6)^11`

Calculus, MET1 2019 VCAA 5

Let  `f: R\ text(\{1}) -> R, \ f(x) = 2/(x-1)^2 + 1`.

    1. Evaluate  `f(-1)`.   (1 mark)

    2. Sketch the graph of `f` on the axes below, labelling all asymptotes with their equations.   (2 marks)

        

  2. Find the area bounded by the graph of `f`, the `x`-axis, the line  `x = -1`  and the line  `x = 0`.   (2 marks)

Show Answers Only
    1. `3/2`
    2. `text(See Worked Solutions)`
  2. `2`
Show Worked Solution
a.i.    `f(-1)` `= 2/(-1-1)^2 + 1`
    `= 3/2`

​

a.ii.     

 

b.    `text(Area)` `= int_(-1)^0 2/(x-1)^2 + 1\ dx`
    `= int_(-1)^0 2(x-1)^(-2) + 1\ dx`
    `= [-2(x-1)^(-1) + x]_(-1)^0`
    `= [((-2)/-1 + 0)-((-2)/-2-1)]`
    `= 2`

L&E, 2ADV E1 SM-Bank 14

The spread of a highly contagious virus can be modelled by the function

`f(x) = 8000/(1 + 1000e^(−0.12x))`

Where `x` is the number of days after the first case of sickness due to the virus is diagnosed and `f(x)` is the total number of people who are infected by the virus in the first `x` days.

  1. Calculate `f(0)`.   (1 mark)

  2. Find the value of `f(365)` and interpret it result.   (2 marks)

Show Answers Only
  1. `7.99…`
  2. `text(After 1 year, the model predicts the total number)`
    `text(of people infected by the virus is 8000.)`
Show Worked Solution
i.   `f(0)` `= 8000/(1 + 1000e^0)`
    `= 8000/1001`
    `= 7.99…`

 

ii.    `f(365)` `= 8000/(1 + 1000e^(−0.12 xx 365))`
    `= 8000/(1 + 1000e^(−43.8))`
    `~~ 8000`

 
`text(After 1 year, the model predicts the total number)`

`text(of people infected by the virus is 8000.)`

Calculus, 2ADV C2 EQ-Bank 2

Differentiate with respect to `x`:

`10^(5x^2 - 3x)`.  (2 marks)

Show Answers Only

`(dy)/(dx) = ln 10  (10x – 3) * 10^(5x^2 – 3x)`

Show Worked Solution

`y = 10^(5x^2 – 3x)`

TIP: The new Advanced reference sheet can be used here!

`(dy)/(dx) = ln 10  (10x – 3) * 10^(5x^2 – 3x)`

 

Vectors, EXT1 V1 SM-Bank 20

Consider the vector  `underset~a = underset~i + sqrt3underset~j`, where  `underset~i`  and  `underset~j`  are unit vectors in the positive direction of the `x` and `y` axes respectively.

  1. Find the unit vector in the direction of  `underset~a`.    (1 mark)

  2. Find the acute angle that  `underset~a`  makes with the positive direction of the `x`-axis.   (1 mark)

  3. The vector  `underset~b = m underset~i - 2underset~j`.

     

    Given that  `underset~b`  is perpendicular to  `underset~a`, find the value of  `underset~m`.   (1 mark)

Show Answers Only
  1. `1/2(underset~i + sqrt3underset~j)`
  2. `60°`
  3. `2sqrt3`
Show Worked Solution

i.   `underset~a = underset~i + sqrt3underset~j`

`|underset~a| = sqrt(1 + (sqrt(3))^2) = 2`

`overset^a = (underset~a)/(|underset~a|) = 1/2(underset~i + sqrt3underset~j)`

 

ii.   `text(Solution 1)`

`underset~a\ =>\ text(Position vector from)\ \ O\ \ text{to}\ \ (1, sqrt3)`

`tan theta` `=sqrt3`  
`:. theta` `=60°`  
     

`text(Solution 2)`

`text(Angle with)\ xtext(-axis = angle with)\ \ underset~b = underset~i`

`underset~a · underset~i = 1 xx 1 = 1`

`underset~a · underset~i` `= |underset~a||underset~i|costheta`
`1` `= 2 xx 1 xx costheta`
`costheta` `= 1/2`
`:. theta` `= 60°`

 

iii.   `underset~b = m underset~i – 2underset~j`

`underset~a · underset~b = [(1),(sqrt3)] · [(m),(−2)] = m – 2sqrt3`

`text(S)text(ince)\ underset~a ⊥ underset~b:`

`m – 2sqrt3` `= 0`
`m` `= 2sqrt3`

Vectors, EXT1 V1 SM-Bank 19

Consider the following vectors

`overset(->)(OA) = 2underset~i + 2underset~j,\ \  overset(->)(OB) = 3underset~i - underset~j,\ \ overset(->)(OC) = 5underset~i + 3underset~j`

  1. Find  `overset(->)(AB)`.  (1 mark)

  2. The points `A`, `B` and `C` are vertices of a triangle. Prove that the triangle has a right angle at `A`.  (2 marks)

  3. Find the length of the hypotenuse of the triangle.  (1 mark)

Show Answers Only
  1. `underset~i – 3underset~j`
  2. `text(See Worked Solutions)`
  3. `2sqrt5`
Show Worked Solution

i.  `text(Find)\ overset(->)(AB):`

COMMENT: Many teachers recommend column vector notation to simplify calculations and minimise errors – we agree!

`overset(->)(OA) = [(2),(2)],\ \ overset(->)(OB)[(3),(−1)]`

`overset(->)(AB)` `= overset(->)(OB) – overset(->)(OA)`
  `= [(3),(−1)] – [(2),(2)]`
  `= [(1),(−3)]`
  `= underset~i – 3underset~j`

 

ii.    `overset(->)(AC)` `= overset(->)(OC) – overset(->)(OA)`
    `= [(5),(3)] – [(2),(2)]`
    `= [(3),(1)]`
    `= 3underset~i + underset~j`

 

`overset(->)(AB) · overset(->)(AC)` `= 1 xx 3 + −3 xx 1=0`

`=> AB ⊥ AC`

`:. DeltaABC\ text(has a right angle at)\ A.`

 

iii.   `overset(->)(BC)\ text(is the hypotenuse)`

`overset(->)(BC)` `= overset(->)(OC) – overset(->)(OB)`
  `= [(5),(3)] – [(3),(−1)]`
  `= [(2),(4)]`
`|overset(->)(BC)|` `=\ text(length of hypotenuse)`
  `= sqrt(2^2 + 4^2)`
  `= sqrt(20)`
  `= 2sqrt5`

Vectors, EXT1 V1 SM-Bank 16 MC

The vectors  `underset~a = 2underset~i + m underset~j`  and  `underset~b = m^2underset~i - underset~j`  are perpendicular for

A.   `m = −2`  and  `m = 0`

B.   `m = 2`  and  `m = 0`

C.   `m = -1/2`  and  `m = 0`

D.   `m = 1/2`  and  `m = 0`

Show Answers Only

`D`

Show Worked Solution

`underset ~a ⊥ underset ~b\ \ =>\ \ underset ~a ⋅ underset ~b=0`

`underset ~a ⋅ underset ~b` `= 2m^2 + m(-1)`
`0` `= 2m^2 – m`
`0` `= m(2m – 1)`

 
`:. m = 0, quad m = 1/2`

`=> D`

Vectors, EXT1 V1 SM-Bank 15

Consider the vectors

`underset~a = 6underset~i + 2underset~j,\ \ underset~b = 2underset~i - m underset~j`

  1. Calculate  `2underset~a - 3underset~b`.  (1 mark)

  2. Find the values of  `m`  for which  `|underset~b| = 3sqrt2`.  (2 marks)

  3. Find the value of  `m`  such that  `underset~a`  is perpendicular to  `underset~b`.  (1 mark)

Show Answers Only
  1. `[(6),(4 + 3m)]`
  2. `±sqrt14`
  3. `6`
Show Worked Solution
i.    `2underset~a – 3underset~b` `= 2[(6),(2)] – 3[(2),(−m)]`
    `= [(12),(4)] – [(6),(−3m)]`
    `= [(6),(4 + 3m)]`

 

ii.   `underset~a = [(6),(2)], \ \ underset~b = [(2),(−m)]`

`|underset~b|` `= sqrt(4 + m^2)`
`3sqrt2` `= sqrt(4 + m^2)`
`18` `= 4 + m^2`
`m^2` `= 14`
`m` `= ±sqrt14`

 

iii.   `text(If)\ \ underset~a ⊥ underset~b \ => \ underset~a · underset~b = 0`

`6 xx 2 + 2 xx – m` `= 0`
`2m` `= 12`
`:. m` `= 6`

Vectors, EXT1 V1 SM-Bank 12

Find the projection of  `underset~a`  onto  `underset~b`  given  `underset~a = 2underset~i + underset~j`  and  `b = 3underset~i - 2underset~j`.  (2 marks)

Show Answers Only

`12/13underset~i – 8/13underset~j`

Show Worked Solution

`underset~a = [(2),(1)],\ \ underset~b = [(3),(−2)]`

COMMENT: Many teachers recommend column vector notation to simplify calculations and minimise errors – we agree!

`text(proj)_(underset~b) underset~a` `= (underset~a · underset~b)/(underset~b · underset~b) xx underset~b`
  `= (6 – 2)/(9 + 4)(3underset~i – 2underset~j)`
  `= 4/13(3underset~i – 2underset~j)`
  `= 12/13underset~i – 8/13underset~j`

Vectors, EXT1 V1 SM-Bank 10

In the quadrilateral  `PQRS`, `T` lies on  `SR`  such that  `ST : TR = 3 : 1`.
 


 

  1. Find  `overset(->)(TS)`  in terms of  `underset~u`,  `underset~v`  and  `underset~w`.   (1 mark)

  2. Hence, find  `overset(->)(TP)`  in terms of  `underset~u`,  `underset~v`  and  `underset~w`.   (1 mark)

Show Answers Only
  1. `3/4(underset~w-underset~u-underset~v)`
  2. `1/4 underset~u + 3/4 underset~w-3/4 underset~v`
Show Worked Solution

i.   `overset(->)(TS) = 3/4 xx-overset(->)(SR)`

`overset(->)(SR) = underset~u + underset~v-underset~w`

`:. overset(->)(TS)` `= 3/4 xx − (underset~u + underset~v-underset~w)`
  `= 3/4(underset~w-underset~u-underset~v)`

 

ii.    `overset(->)(TP)` `= overset(->)(SP) + overset(->)(TS)`
    `= underset~u + 3/4(underset~w-underset~u-underset~v)`
    `= 1/4 underset~u + 3/4 underset~w-3/4 underset~v`

Calculus, EXT2 C1 2019 HSC 15c

  1. Show that  `int_0^1 x/(x + 1)^2\ dx = ln 2 - 1/2`.  (2 marks)


  2. Let  `I_n = int_0^1 x^n/(x + 1)^2\ dx`.

     


    Show that  `I_n = 1/(2(n - 1)) - n/(n - 1) I_(n - 1)\ \ text(for)\ \ n >= 2`.  (3 marks)


  3. Evaluate  `I_3`.  (2 marks)

Show Answers Only
  1. `text(Proof)\ text{(See Worked Solutions)}`
  2. `text(Proof)\ text{(See Worked Solutions)}`
  3. `text(See Worked Solutions)`
Show Worked Solution

i.    `text(Show)\ \ int_0^1 x/(x + 1)^2\ dx = ln 2 – 1/2`

`text(Let)\ \ u = x + 1 \ => \ x = u – 1`

`(du)/(dx) = 1 \ => \ du = dx`
 

`text(When)\ \ x = 1,\ \ u = 2`

`text(When)\ \ x = 0,\ \ u = 1`

`int_0^1 x/(x + 1)^2\ dx` `= int_1^2 (u – 1)/(u^2)\ du`
  `= int_1^2 1/u\ du – int_1^2 1/u^2\ du`
  `= [ln u]_1^2 + [1/u]_1^2`
  `= ln 2 – ln 1 + 1/2 – 1`
  `= ln 2 – 1/2`

 
ii.    `I_u = int_0^1 x^n/(x + 1)^2\ dx`

`u = x^n` `v prime = 1/(x + 1)^2`
`u prime = nx^(n – 1)` `v = -1/{(x + 1)}`

 

`I_n` `= [uv]_0^1 – int_0^1 u prime v\ dx`
  `= [(-x^n)/(x + 1)]_0^1 + int_0^1 (n x^(n – 1))/(x + 1)\ dx`
  `= (-1/2 – 0) + n int_0^1 (x^(n – 1) (x + 1))/(x + 1)^2\ dx`
  `= -1/2 + n int_0^1 x^n/(x + 1)^2 + (x^(n – 1))/(x + 1)^2\ dx`
  `= -1/2 + n I_n + n I_(n – 1)`
`nI_n – I_n` `= 1/2 – n I_(n – 1)`
`I_n(n – 1)` `= 1/2 – n I_(n – 1)`
`:. I_n` `= 1/(2(n – 1)) – n/(n – 1) I_(n – 1)`

 

iii.    `I_1` `= ln 2 – 1/2`
  `I_2` `= 1/(2(2 – 1)) – 2/{(2 – 1)} I_1`
    `= 1/2 – 2 I_1`
    `= 1/2 – 2 ln 2 + 1`
    `= 3/2 – 2 ln 2`

 

`:. I_3` `= 1/4 – 3/2(3/2 – 2 ln 2)`
  `= 1/4 – 9/4 + 3 ln 2`
  `= 3 ln 2 – 2`

Proof, EXT2 P2 2019 HSC 14c

  1. Show that  `cot x - cot 2x = text(cosec)\ 2x`.  (2 marks)

  2. Use mathematical induction to prove that, for all  `n >= 1`,

`sum_(r = 1)^n\ text(cosec)(2^r x) = cot x - cot(2^n x)`.  (2 marks)

Show Answers Only
  1. `text(Proof)\ text{(See Worked Solutions)}`
  2. `text(Proof)\ text{(See Worked Solutions)}`
Show Worked Solution

i.    `text(Show)\ \ cot x – cot 2x = text(cosec)\ 2x`

`text(LHS)` `= (cos x)/(sin x) – 1/(tan 2x)`
  `= (cos x)/(sin x) – (1 – tan^2 x)/(2 tan x)`
  `= (cos x)/(sin x) – ((1 – (sin^2 x)/(cos^2 x))/(2 (sin x)/(cos x)))`
  `= (cos x)/(sin x) – ((cos^2 x – sin^2 x)/(2 sin x cos x))`
  `= (2 cos^2 x – cos^2 x + sin^2 x)/(2 sin x cos x)`
  `= 1/(sin 2x)`
  `= text(cosec)\ 2x`
  `= ­text(RHS)`

 

ii.    `text(Prove)\ \ sum_(r = 1)^n\ text(cosec)(2^rx) = cot x – cot 2^n x\ \ text(for)\ \ n >= 1`

`text(Show true for)\ \ n = 1:`

♦ Mean mark 45%.

`text(LHS) = text(cosec)(2x)`

`text(RHS) = cot x – cot 2x = text(cosec)(2x)\ \ text{(using part (i))}`

`:.\ text(True for)\ \ n = 1`
 

`text(Assume true for)\ \ n = k:`

`text(cosec)\ 2x + text(cosec)\ 4x + … + text(cosec)\ 2^rx = cot x – cot 2^r x`

`text(Prove true for)\ \ n = k + 1:`

`text(i.e. cosec)\ 2x + … + text(cosec)\ 2^r x + text(cosec)\ 2^(r + 1) x = cot x – cot 2^(r + 1) x`

`text(LHS)` `= cot x – cot 2^r x + text(cosec)\ 2^(r + 1) x`
  `= cot x – cot 2^r x + text(cosec)\ (2.2^r x)`
  `= cot x – cot 2^r x + cot 2^r x – cot 2^(r + 1) x`
  `= cot x – cot 2^(r + 1) x`
  `= ­text(RHS)`

 
`:.\ text(True for)\ \ n=k+1`

`:.\ text(S)text(ince true for)\ \ n=1, text(by PMI, true for integral)\ \ n>=1.`

Mechanics, EXT2 M1 2019 HSC 14b

A parachutist jumps from a plane, falls freely for a short time and then opens the parachute. Let t be the time in seconds after the parachute opens, `x(t)`  be the distance in metres travelled after the parachute opens, and  `v(t)`  be the velocity of the parachutist in `text(ms)^(-1)`.

The acceleration of the parachutist after the parachute opens is given by

`ddot x = g - kv,`

where `g\ text(ms)^(-2)` is the acceleration due to gravity and `k` is a positive constant.

  1. With an open parachute the parachutist has a terminal velocity of  `w\ text(ms)^(-1)`.

     

    Show that  `w = g/k`.  (1 mark)

    At the time the parachute opens, the speed of descent is `1.6 w\ text(ms)^(-1)`.

  2. Show that it takes  `1/k log_e 6`  seconds to slow down to a speed of `1.1w\ text(ms)^(-1)`.  (4 marks)

  3. Let  `D`  be the distance the parachutist travels between opening the parachute and reaching the speed `1.1w\ text(ms)^(-1)`.

     

     

    Show that  `D = g/k^2 (1/2 + log_e 6)`.  (3 marks)

Show Answers Only
  1. `text(Proof)\ text{(See Worked Solutions)}`
  2. `text(Proof)\ text{(See Worked Solutions)}`
  3. `text(Proof)\ text{(See Worked Solutions)}`
Show Worked Solution

i.   `v_T=w\ \  text(when)\ \ ddot x = 0`

`0` `= g – kw`
`w` `= g/k`

 

ii.   `text(Show)\ \ t = 1/k log_e 6\ \ text(when)\ \ v = 1.1w`

`(dv)/(dt)` `= g – kv`
`(dt)/(dv)` `= 1/(g – kv)`
`t` `= int 1/(g – kv)\ dv`
  `= -1/k ln(g – kv) + C`

 
`text(When)\ \ t = 0,\ \ v = 1.6w`

`0` `= -1/k ln(g – 1.6 kw) + C`
`C` `= 1/k ln(g – 1.6 kw)`
`t` `= 1/k ln (g – 1.6kw) – 1/k ln(g – kv)`
  `= 1/k ln((g – 1.6 kw)/(g – kv))`

 
`text(Find)\ \ t\ \ text(when)\ \ v = 1.1w`

`t` `= 1/k ln((g – 1.6 k xx g/k)/(g – 1.1k xx g/k))`
  `=1/k ln((g – 1.6 g)/(g – 1.1g))`
  `=1/k((-0.6g)/(-0.1g))`
  `= 1/k ln 6`

 

iii.    `v ⋅ (dv)/(dx)` `= g – kv`
  `(dv)/(dx)` `= (g – kv)/v`
  `(dx)/(dv)` `= v/(g – kv)`
  `x` `= int v/(g – kv)\ dv`
    `= 1/k int (kv)/(g – kv)\ dv`
    `= -1/k int 1 – g/(g – kv)\ dv`

 

`:. D` `= -1/k int_(1.6w)^(1.1w) 1 – g/(g – kv)\ dv`
  `= 1/k int_(1.1w)^(1.6w) 1 – g/(g – kv)\ dv`
  `= 1/k[v + g/k ln (g – kv)]_(1.1w)^(1.6w)`
  `= g/k^2[(kv)/g + ln (g – kv)]_(1.1w)^(1.6w)`
  `= g/k^2[((1.6kw)/g + ln (g – 1.6kw)) – ((1.1 kw)/g + ln (g – 1.1kw))]`
  `= g/k^2[1.6 + ln ((g – 1.6kw)/(g – 1.1kw)) – 1.1]`
  `= g/k^2(0.5 + ln 6)`

Mechanics, EXT2* M1 2019 HSC 13c

Two objects are projected from the same point on a horizontal surface. Object 1 is projected with an initial velocity of  `20\ text(ms)^(-1)` directed at an angle of  `pi/3`  to the horizontal. Object 2 is projected 2 seconds later.

The equations of motion of an object projected from the origin with initial velocity `v` at an angle `theta` to the `x`-axis are

`x = vt cos theta`

`y = -4.9t^2 + vt sin theta`,

where  `t`  is the time after the projection of the object. Do NOT prove these equations.

  1. Show that Object 1 will land at a distance  `(100 sqrt 3)/4.9` m from the point of projection.  (2 marks)

  2. The two objects hit the horizontal plane at the same place and time.

     

    Find the initial speed and the angle of projection of Object 2, giving your answer correct to 1 decimal place.  (3 marks)

Show Answers Only
  1. `text(Proof)\ text{(See Worked Solutions)}`
  2. `24.2\ text(ms)^(-1)`
Show Worked Solution

a.   `text(Object 1:)`

`x` `= 20t cos\ pi/3`
  `= 10t`
`y` `= -4.9t^2 + 20t sin\ pi/3`
  `= -4.9t^2 + 10 sqrt 3 t`

 
`text(Let)\ \ t_1 = text{time of flight (Object 1)}`

`-4.9t_1^2 + 10 sqrt 3 t_1` `= 0`
`t_1(-4.9t_1 + 10 sqrt 3)` `= 0`
`4.9t_1` `= 10 sqrt 3\ \ (t >= 0)`
`t_1` `= (10 sqrt 3)/4.9`

 
`text(Find)\ \ x\ \ text(when)\ \ t_1 = (10 sqrt 3)/4.9:`

`x` `= 10 xx (10 sqrt 3)/4.9`
  `= (100 sqrt 3)/4.9\ text(… as required)`

 

(ii)   `text{Time of flight (Object 2)}= (10 sqrt 3)/4.9 – 2`

♦ Mean mark 42%.

`text(Range)` `= (100 sqrt 3)/4.9`
`(100 sqrt 3)/4.9` `= v((10 sqrt 3)/4.9 – 2) cos theta`
`v cos theta` `= (100 sqrt 3)/4.9 xx 4.9/(10 sqrt 3 – 9.8)`
`v cos theta` `= (100 sqrt 3)/(10 sqrt 3 – 9.8) \ \ \ …\ (1)`

 

`0` `= -4.9t^2 + vt sin theta`
`0` `= -4.9 xx ((10 sqrt 3)/4.9 – 2)^2 + v((10 sqrt 3)/4.9 – 2) sin theta`
`0` `= -4.9((10 sqrt 3 – 9.8)/4.9) + v sin theta`
`v sin theta` `= 10 sqrt 3 – 9.8 \ \ \ …\ (2)`

 
`(2) ÷ (1)`

`tan theta` `= (10 sqrt 3 – 9.8) xx (10 sqrt 3 – 9.8)/(100 sqrt 3)`
  `= 0.3265…`
`:. theta` `= 18.1^@\ text{(1 d.p.)}`

 
`text{Substitute into (2)}`

`:.v` `= (10 sqrt 3 – 9.8) /(sin 18.1^@)`
  `= 24.206`
  `= 24.2\ text(ms)^(-1)\ text{(1 d.p.)}`

Functions, EXT1′ F1 2019 HSC 12d

Consider the function  `f(x) = x^3 - 1`.

  1.  Sketch the graph  `y = |\ f(x)\ |`.  (1 mark)

  2.  Sketch the graph  `y = 1/(f(x))`.  (2 marks)

  3.  Without using calculus, sketch the graph  `y = x/(f(x))`.  (2 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `text(See Worked Solutions)`
  3. `text(See Worked Solutions)`
Show Worked Solution

i.   `y = |\ x^3 – 1\ |`

 

ii.   `y = 1/(x^3 – 1)`

 

iii.   `y = x/(x^3 – 1)`

Calculus, EXT1′ C3 2019 HSC 12b

The diagram shows two straight railway tracks that meet at an angle of  `(2 pi)/3`  at the point `P`.

Trains  `A`  and  `B`  are joined by a cable which is 70 m long.

At time  `t`  seconds, train  `A`  is  `x`  metres from  `P`  and train  `B`  is  `y`  metres from `P`.

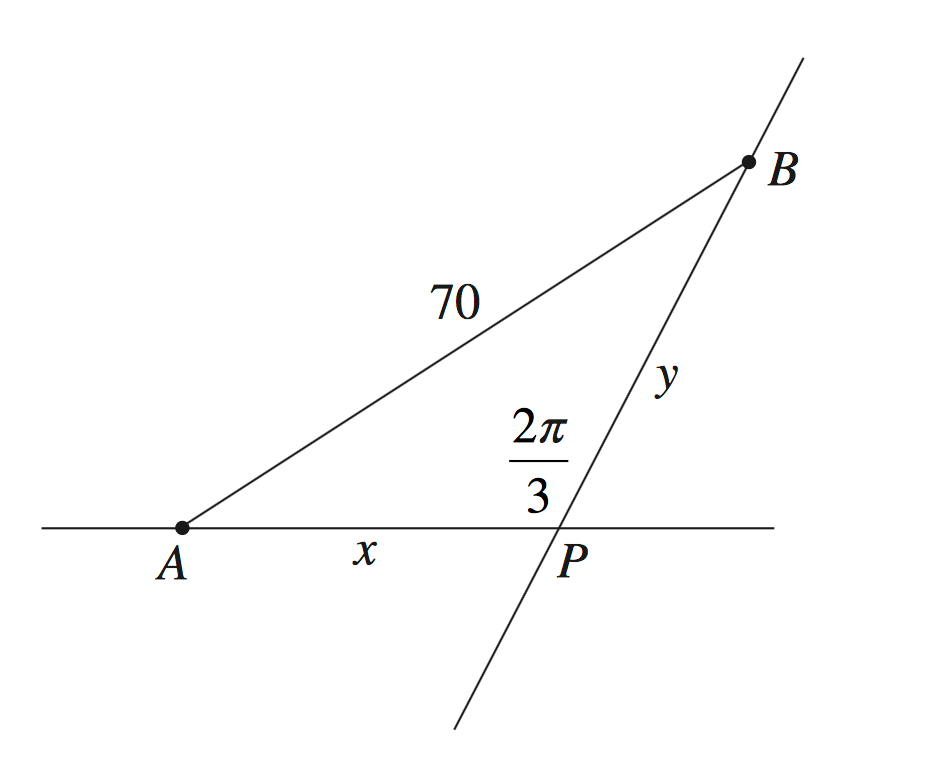
Train  `B`  is towing train  `A`  and is moving at a constant speed of  `4\ text(ms)^(-1)` away from `P`.

  1. Show that  `x^2 + xy + y^2 = 70^2`.  (1 mark)
  2. What is the value of  `(dx)/(dt)`  when train  `A`  is 30 metres from  `P`  and train  `B`  is 50 metres from `P`?  (3 marks)

 

Show Answers Only
  1. `text(Proof)\ text{(See Worked Solutions)}`
  2. `-52/11`
Show Worked Solution

(i)   `text(Using cosine rule):`

`x^2 + y^2 – 2xy cos ((2 pi)/3)` `= 70^2`
`x^2 + y^2 – 2xy xx -1/2` `= 70^2`
`x^2 + xy + y^2` `= 70^2`

 

(ii)    `(dy)/(dt)` `= 4`
  `(dx)/(dt)` `= (dy)/(dt) ⋅ (dx)/(dy)`

 
`text{Differentiate part (i)}:`

`2x + x ⋅ (dy)/(dx) + y + 2y ⋅ (dy)/(dx)` `= 0`
`(dy)/(dx) (x + 2y)` `= -2x – y`
`(dy)/(dx)` `= (-2x – y)/(x + 2y)`

 
`text(When)\ \ x = 30,\ \ y = 50`

`(dx)/(dt)` `= 4 xx (30 + 2(50))/(-2(30) – 50)`
  `= 4 xx -130/110`
  `= -52/11`

Complex Numbers, EXT2 N1 2019 HSC 11e

Let  `z = -1 + i sqrt 3`.

  1. Write  `z`  in modulus-argument form.  (2 marks)

  2. Find  `z^3`, giving your answer in the form  `x + iy`, where  `x`  and  `y`  are real numbers.  (2 marks)

Show Answers Only
  1. `z = 2 text(cis) (2 pi)/3`
  2. `8 + 0i`
Show Worked Solution
i.   `|\ z\ |` `= -1 + i sqrt 3`
    `= sqrt((-1)^2 + (sqrt 3)^2)`
    `= 2`

 

  `tan theta` `= -sqrt 3`
  `text(arg)(z)` `= (2 pi)/3`
  `:. z` `= 2 text(cis) (2 pi)/3`

 

ii.   `z^3 = 2^3 [cos(3 xx (2 pi)/3) + i sin (3 xx (2 pi)/3)]\ \ \ text{(by De Moivre)}`

`= 8(cos 2 pi + i sin 2 pi)`

`= 8(1 + 0i)`

`= 8 + 0i`

Calculus, EXT2 C1 2019 HSC 3 MC

Which expression is equal to  `int x cos x\ dx`?

  1. `-x sin x + cos x + C`
  2. `-x sin x - cos x + C`
  3. `x sin x + cos x + C`
  4. `x sin x - cos x + C`
Show Answers Only

`C`

Show Worked Solution
`u = x` `v prime = cos x`
`u prime = 1` `v = sin x`

 

`int uv prime\ dx` `= uv – int u prime v\ dx`
  `= x sin x – int sin x\ dx`
  `= x sin x + cos x + C`

 
`=>   C`

Financial Maths, STD1 F2 2019 HSC 35

A bank offers two different savings accounts.

Account `X` offers simple interest of 7% per annum.
Account `Y` offers compound interest of 6% per annum compounded yearly.

The table displays the future values of $20 000 invested in each account for the first 2 years.
 


  

  1. How much more money is there in Account `X` than in Account `Y` at the end of 2 years?  (1 mark)

  2. Show that there would be more money in Account `Y` than in Account `X` at the end of 8 years.  (3 marks)

Show Answers Only
  1. `$328`
  2. `text(See Worked Solutions)`
Show Worked Solution
a.    `text(Extra money in)\ \ X` `= 22\ 800 – 22\ 472`
    `= $328`

 

b.   `text(Account)\ X:`

♦ Mean mark part (b) 30%.

`I` `= Prn`
  `= 20\ 000 xx 7/100 xx 8`
  `= 11\ 200`

 
`=> text(Balance)\ X = 20\ 000 + 11\ 200 = $31\ 200`
 

`text(Account)\ Y:`

`FV` `= PV(1 + r)^n`
  `= 20\ 000(1 + 6/100)^8`
  `= $31\ 876.96`

 
`:. text(After 8 years, there’s more money in Account)\ Y.`

Algebra, STD1 A3 2019 HSC 23

Five rabbits were introduced onto a farm at the start of 2018. At the start of 2019 there were 10 rabbits on the farm. It is predicted that the number of rabbits on the farm will continue to double each year.

  1. Complete the following table.  (1 mark)
     


     

  2. Complete the scale on the vertical axis and then plot the data from part (a) on the grid.  (2 marks)


      

  3. Would a linear model or an exponential model better fit this graph? Explain the reason for your answer.  (1 mark)

Show Answers Only
  3. `text(Exponential model – the graph isn’t a straight line.)`
    `text(The number of rabbits grow at an increasing rate.)`
Show Worked Solution
a.   

 

b.   

♦ Mean mark part (c) 25%.

c.   `text(Exponential model – the graph isn’t a straight line.)`

`text(The number of rabbits grow at an increasing rate.)`

Measurement, STD1 M5 2019 HSC 20

The plan of the lower level of a small house is shown.


 

  1. How many windows are shown on the plan?  (1 mark)

  2. What is the actual perimeter, in metres, of the shaded part of the kitchen floor?  (2 marks)

Show Answers Only
  1. `text(6 windows)`
  2. `6.5\ text(metres)`
Show Worked Solution

a.   `text(6 windows)`

 

b.    `text(Plan Perimeter)` `= 2 xx 3\ text(units) + 2 xx 3.5\ text(units)`
    `= 13\ text(units)`

 

`:.\ text(Actual perimeter)` `= 13 xx 0.5`
  `= 6.5\ text(metres)`

Proof, EXT1 P1 2019 HSC 14a

Prove by mathematical induction that, for all integers `n >= 1`,

`1(1!) + 2(2!) + 3(3!) + … + n(n!) = (n + 1)! - 1`.  (3 marks)

Show Answers Only

`text(Proof)\ text{(See Worked Solutions)}`

Show Worked Solution

`text(Prove true for)\ n = 1:`

`text(LHS) = 1(1!) = 1`

`text(RHS) = (1 + 1)! – 1 = 2! – 1 = 1 = text(LHS)`

`:.\ text(True for)\ \ n = 1`
 

`text(Assume true for)\ \ n = k:`

`1(1!) + 2(2!) + … + k(k!) = (k + 1)! – 1`
 

`text(Prove true for)\ \ n = k + 1`

`text(i.e.)\ \ underbrace(1(1!) + 2(2!) + … + k(k!))_((k + 1)! – 1) + (k + 1)(k + 1)! = (k + 2)! – 1`

`text(LHS)` `= (k + 1)! – 1 + (k + 1)(k + 1)!`
  `= (k + 1)! [1 + (k + 1)] – 1`
  `= (k + 1)!(k + 2) – 1`
  `= (k + 2)! – 1`

 
`\Rightarrow\ \ text(True for)\ \ n = k + 1`

`:.\ text(S)text(ince true for)\ \ n = 1,\ text(by PMI, true for integral)\ \ n >= 1.`

Measurement, STD1 M4 2019 HSC 6 MC

When blood pressure is measured, two numbers are recorded: systolic pressure and diastolic pressure. If the measurements recorded are 130 systolic and 85 diastolic, then the blood pressure is written as '130 over 85'.

The bars on the graph indicate the healthy ranges of blood pressure for people of various ages.
 


 

Which person has both blood pressure measurements in the healthy range for their age?

  1. Stella aged 23 with blood pressure 120 over 72
  2. Shane aged 35 with blood pressure 124 over 90
  3. Jon aged 54 with blood pressure 137 over 94
  4. Annie aged 61 with blood pressure 142 over 88
Show Answers Only

`D`

Show Worked Solution

`text(Annie has both measures in the healthy range.)`

♦ Mean mark 48%.

 
`=> D`

Measurement, STD1 M4 2019 HSC 3 MC

Sugar is sold in four different sized packets.

Which is the best buy?

  1.  100 g for $0.40
  2.  500 g for $1.65
  3.  1 kg for $3.50
  4.  2 kg for $6.90
Show Answers Only

`B`

Show Worked Solution

`text(Price per kilogram:)`

`100\ text(g) -> 10 xx 0.40 = $4.00`

`500\ text(g) -> 2 xx 1.65 = $3.30`

`1\ text(kg) -> $3.50`

`2\ text(kg) -> 6.90 ÷ 2 = $3.45`

`=> B`

Calculus, EXT1 C1 2019 HSC 12d

A refrigerator has a constant temperature of 3°C. A can of drink with temperature 30°C is placed in the refrigerator.

After being in the refrigerator for 15 minutes, the temperature of the can of drink is 28°C.

The change in the temperature of the can of drink can be modelled by  `(dT)/(dt) = k(T - 3)`,  where `T` is the temperature of the can of drink, `t` is the time in minutes after the can is placed in the refrigerator and `k` is a constant.

  1. Show that  `T = 3 + Ae^(kt)`, where `A` is a constant, satisfies

     

    `qquad(dT)/(dt) = k(T - 3)`.  (1 mark)

  2. After 60 minutes, at what rate is the temperature of the can of drink changing?   (3 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `-0.10^@\ text{C per minute (decreasing)}`
Show Worked Solution

a.    `T = 3 + Ae^(kt)`

`(dT)/(dt)` `= k ⋅ Ae^(kt)`
  `= k (3 + Ae^(kt) – 3)`
  `= k(T – 3)`

 

b.   `text(When)\ \ t = 0,\ \ T = 30,`

`30` `= 3 + Ae^0`
`A` `= 27`

 
`text(When)\ \ t = 15,\ \ T = 28,`

`28` `= 3 + 27e^(15k)`
`25` `= 27e^(15k)`
`e^(15k)` `= 25/27`
`15k` `= ln (25/27)`
`k` `= 1/15 xx ln (25/27)`

 
`text(Find)\ \ (dT)/(dt)\ \ text(when)\ \ t = 60:`

`(dT)/(dt)` `= 1/15 xx ln (25/27) xx 27e^(60 xx 1/15 ln (25/27))`
  `= 27/15 xx ln (25/27) xx e^(4 ln (25/27))`
  `=27/15 xx ln(25/27) xx (25/27)^4`
  `= -0.1018…`
  `= -0.10^@ text{C per minute (decreasing)}`

Calculus, EXT1 C1 2019 HSC 12a

Distance `A` is inversely proportional to distance `B`, such that  `A = 9/B`  where `A` and `B` are measured in metres. The two distances vary with respect to time. Distance `B` is increasing at a rate of  `0.2\ text(ms)^(-1)`.

What is the value of  `(dA)/(dt)`  when  `A = 12`?  (3 marks)

Show Answers Only

`-3.2\ text(ms)^(-1)`

Show Worked Solution

`A = 9/B,\ \ (dB)/(dt) = 0.2\ \ text{(given)}`

`(dA)/(dB)` `= -9/B^2`
`(dA)/(dt)` `= (dA)/(dB) xx (dB)/(dt)`
  `= -9/B^2 xx 0.2`

 
`text(When)\ \ A = 12\ \ =>\ \ B = 3/4 :`

`(dA)/(dt)` `= -9/(3/4)^2 xx 0.2`
  `= -3.2\ text(ms)^(-1)`

Statistics, EXT1 S1 2019 HSC 11f

Prize-winning symbols are printed on 5% of ice-cream sticks. The ice-creams are randomly packed into boxes of 8.

  1. What is the probability that a box contains no prize-winning symbols?  (1 mark)

  2. What is the probability that a box contains at least 2 prize-winning symbols?  (2 marks)

Show Answers Only
  1. `0.95^8`
  2. `5.72 text(%)`
Show Worked Solution

i.   `text(Chances of any stick winning:)`

`P(W) = 0.05`

`P(barW) = 0.95`

`P (text{In box of 8, all}\ barW)`

`= 0.95^8`

 

ii.   `P\ text{(at least two winners in a box)}`

`= 1 – P text{(1 winner)} – P text{(0 winners)}`

`= 1 – \ ^8 C_1 xx 0.95^7 xx 0.05^1 – \ ^8 C_0 xx 0.95^8`

`= 0.05724…`

`= 5.72 text{%   (to 2 d.p.)}`

Functions, EXT1 F2 2019 HSC 11d

Find the polynomial  `Q(x)`  that satisfies  `x^3 + 2x^2-3x-7 = (x-2) Q(x) + 3`.  (2 marks)

Show Answers Only

`Q(x ) = x^2 + 4x + 5`

Show Worked Solution
`(x-2) ⋅ Q(x) + 3` `= x^3 + 2x^2-3x-7`
`(x-2) ⋅ Q(x)` `= x^3 + 2x^2-3x-10`

 

`:. Q(x ) = x^2 + 4x + 5`

Functions, EXT1 F1 2019 HSC 11b

For what values of  `x`  is  `x/(x + 1) < 2`?  (3 marks)

Show Answers Only

`x < -2 or x > -1`

Show Worked Solution

`x/(x + 1) < 2`

`text(Multiply b.s. by)\ \ (x + 1)^2`

`x(x + 1)` `< 2(x + 1)^2`
`x^2 + x` `< 2x^2 + 4x + 2`
`0` `< x^2 + 3x + 2`
`0` `< (x + 2)(x + 1)`

 
`text(From graph:)`

`x < -2 or x > -1`

Functions, 2ADV’ F2 2019 HSC 4 MC

The diagram shows the graph of  `y = f(x)`.
 


 

Which equation best describes the graph?

A.     `y = x/(x^2 - 1)`

B.     `y = x^2/(x^2 - 1)`

C.     `y = x/(1 - x^2)`

D.     `y = x^2/(1 - x^2)`

Show Answers Only

`B`

Show Worked Solution

`text(By elimination:)`

`text(Graph is an even function)`

`=> f(x) = f(-x)`

`:.\ text(Eliminate A and C)`
 

`text(When)\ -1 < x < 1,\ \ y <= 0`

`:.\ text(Eliminate D)`

`=>  B`

Algebra, STD2 A4 2019 HSC 36

A small business makes and sells bird houses.

Technology was used to draw straight-line graphs to represent the cost of making the bird houses `(C)` and the revenue from selling bird houses `(R)`. The `x`-axis displays the number of bird houses and the `y`-axis displays the cost/revenue in dollars.
 


 

  1. How many bird houses need to sold to break even?  (1 mark)

  2. By first forming equations for cost `(C)` and revenue `(R)`, determine how many bird houses need to be sold to earn a profit of $1900.  (3 marks)

Show Answers Only
  1. `20`
  2. `96`
Show Worked Solution

a.   `20\ \ (xtext(-value at intersection))`

 

b.   `text(Find equations of both lines):`

♦♦ Mean mark 28%.

`(0, 500)\ text(and)\ (20, 800)\ text(lie on)\ \ C`

`m_C = (800-500)/(20-0) = 15`

`=> C = 500 + 15x`
 

`(0,0)\ text(and)\ (20, 800)\ text(lie on)\ \ R`

`m_R = (800-0)/(20-0) = 40`

`=> R = 40x`
 

`text(Profit) = R-C`

`text(Find)\ \ x\ \ text(when Profit = $1900:)`

`1900` `= 40x-(500 + 15x)`
`25x` `= 2400`
`x` `= 96`

Algebra, STD2 A4 2019 HSC 33

The time taken for a car to travel between two towns at a constant speed varies inversely with its speed.

It takes 1.5 hours for the car to travel between the two towns at a constant speed of 80 km/h.

  1. Calculate the distance between the two towns.  (1 mark)

  2. By first plotting four points, draw the curve that shows the time taken to travel between the two towns at different constant speeds.  (3 marks)

Show Answers Only
  1. `120\ text(km)`
  2.  
Show Worked Solution
a.    `D` `= S xx T`
    `= 80 xx 1.5`
    `= 120\ text(km)`

 
b.   

\begin{array} {|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} \ \ s\ \  \rule[-1ex]{0pt}{0pt} & 20 & 40 & 60 & 80 \\
\hline
\rule{0pt}{2.5ex} t \rule[-1ex]{0pt}{0pt} & 6 & 3 & 2 & 1.5 \\
\hline
\end{array}

Calculus, 2ADV C3 2019 HSC 14b

The derivative of a function  `y = f(x)`  is given by  `f^{′}(x) = 3x^2 + 2x-1`.

  1. Find the `x`-values of the two stationary points of  `y = f(x)`, and determine the nature of the stationary points.  (2 marks)

  2. The curve passes through the point  `(0, 4)`.

     

    Find an expression for  `f(x)`.  (2 marks)

  3. Hence sketch the curve, clearly indicating the stationary points.  (2 marks)

  4. For what values of `x` is the curve concave down?  (1 mark)

Show Answers Only
  1. `x = 1/3\ \ text{(min)}`
    `x = -1\ \ text{(max)}`
  2. `f(x) = x^3 + x^2-x + 4`
  3. `text(See Worked Solution)`
  4. `x < -1/3`
Show Worked Solution

a.    `f^{′}(x) = 3x^2 + 2x-1`

`f^{″}(x) = 6x + 2`

`text(S.P.’s when)\ \ f^{′}(x) = 0`

`3x^2 + 2x-1` `= 0`
`(3x-1)(x + 1)` `= 0`

 
`x = 1/3 or -1`

`text(When)\ x = 1/3,`

`f^{″}(x) = 4 > 0 =>\ text(MIN)`
 

`text(When)\ x = -1,`

`f^{″}(x)= -4 < 0 =>\ text(MAX)`

 

b.    `f(x)` `= int f^{′}(x)\ dx`
    `= int 3x^2 + 2x-1\ dx`
    `= x^3 + x^2-x + c`

 
`(0, 4)\ \ text(lies on)\ \ f(x)\ \ =>\ \ c = 4`

`:. f(x) = x^3 + x^2-x + 4`

 

c.    `text(When)\ \ x = -1,\ \ y = 5`
  `text(When)\ \ x = 1/3,\ \ y = 103/27`

 

 

d.   `text(Concave down when)\ f^{″}(x) < 0`

♦ Mean mark 36%.

`6x + 2` `< 0`
`6x` `< -2`
`x` `< -1/3`

Calculus, 2ADV C4 2019 HSC 13c

  1.  Differentiate  `(ln x)^2`.  (2 marks)

  2.  Hence, or otherwise, find  `int(ln x)/x\ dx`.  (1 mark)

Show Answers Only
  1. `(2 ln x)/x`
  2. `1/2 (ln x)^2 + C`
Show Worked Solution
i.    `y` `= (ln x)^2`
  `(dy)/(dx)` `= 2 ⋅ 1/x ⋅ ln x`
    `= (2 ln x)/x`

♦ Mean mark part (ii) 49%.

ii.    `int (ln x)/x\ dx` `=1/2 int (2 ln x)/x dx`
    `= 1/2 (ln x)^2 +C`

Calculus, EXT1* C1 2019 HSC 12c

The number of leaves, `L(t)`, on a tree `t` days after the start of autumn can be modelled by

`L(t) = 200\ 000e^(-0.14t)`

  1. What is the number of leaves on the tree when  `t = 31`?  (1 mark)

  2. What is the rate of change of the number of leaves on the tree when  `t = 31`?  (2 marks)

  3. For what value of `t` are there 100 leaves on the tree?  (2 marks)

Show Answers Only
  1. `2607\ text(leaves)`
  2. `-365.02…`
  3. `54.3\ text{(1 d.p.)}`
Show Worked Solution

i.  `text(When)\ \ t = 31`

`L(t)` `= 200\ 000 xx e^(-0.14(31))`
  `=2607.305…`
  `= 2607\ text(leaves)`

 

ii.    `L` `= 2000\ 000^(-0.14t)`
  `(dL)/(dt)` `= -0.14 xx 200\ 000 e^(0.14t`
    `= -28\ 000e^(-0.14t)`

 
`text(When)\ \ t = 31,`

`(dL)/(dt)` `= -28\ 000 xx e^(-0.14(31))`
  `= -365.02…`

 
`:.\ text(365 leaves fall per day.)`

 

iii.   `text(Find)\ t\ text(when)\ \ L = 100:`

`100` `= 200\ 000 e^(-0.14t)`
`e^(-0.14t)` `= 0.0005`
`e^(-0.14t)` `= ln 0.0005`
`t` `= (ln 0.0005)/(-0.14)`
  `= 54.292…`
  `= 54.3\ text{(1 d.p.)}`

Financial Maths, 2ADV M1 2019 HSC 12b

In an arithmetic series, the fourth term is 6 and the sum of the first 16 terms is 120.

Find the common difference.  (3 marks)

Show Answers Only

`1/3`

Show Worked Solution

`T_4 = 6,`

`a + 3d = 6\ …\ \ (1)`

`S_16 = 120,`

`16/2(2a + 15d)` `= 120`
`16a + 120d` `= 120\ …\ \ (2)`

 
`text(Substitute)\ \ a = 6 – 3d\ \ text{from (1) into (2):}`

`16(6 – 3d) + 120d` `= 120`
`96 – 48d + 120d` `= 120`
`72d` `= 24`
`d` `= 1/3`

Probability, 2ADV S1 2019 HSC 11f

A bag contains 5 green beads and 7 purple beads. Two beads are selected at random, without replacement.

What is the probability that the two beads are the same colour?  (2 marks)

Show Answers Only

`31/66`

Show Worked Solution

`P\ text{(same colour)}` `= P (GG) + P(PP)`
  `= 5/12 ⋅ 4/11 + 7/12 ⋅ 6/11`
  `= 62/132`
  `= 31/66`