Band 5 – Page 23

Financial Maths, GEN1 2024 VCAA 24 MC

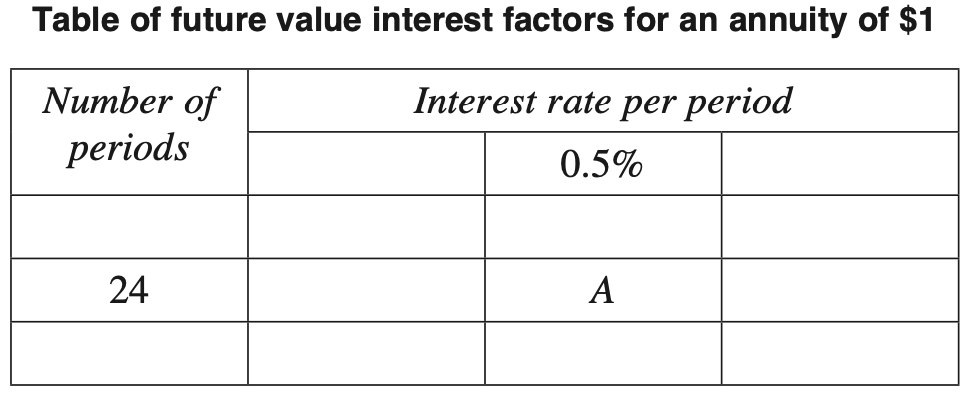
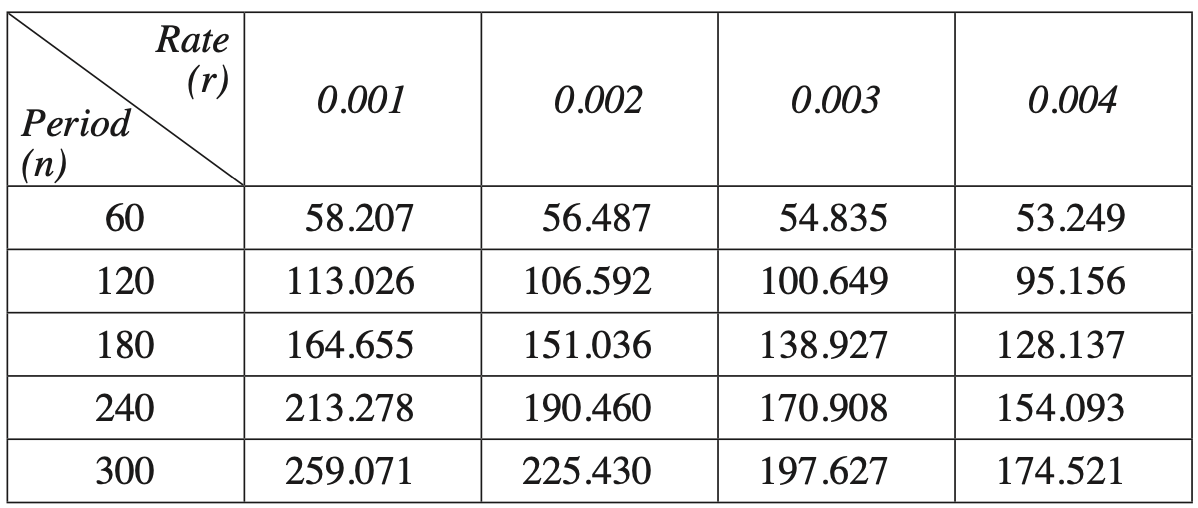
André invested $18 000 in an account for five years, with interest compounding monthly.

He adds an extra payment into the account each month immediately after the interest is calculated.

For the first two years, the balance of the account, in dollars, after $n$ months, $A_n$, can be modelled by the recurrence relation

$A_0=18\,000, \quad A_{n+1}=1.002 A_n+100$

After two years, André decides he would like the account to reach a balance of $30 000 at the end of the five years.

He must increase the value of the monthly extra payment to achieve this.

The minimum value of the new payment for the last three years is closest to

$189.55
$195.45
$202.35
$246.55

Show Answers Only

$A$

Show Worked Solution

$\text{Step 1: Using CAS}$

$\text{Annual interest rate}\ = (1.002-1) \times 12 = 0.024 = 2.4\% $

$\text{Compounding periods (2 years)}\ = 2 \times 12=24$

$\text{Value of investment after 2 years}\ =$21\,340.18$

♦ Mean mark 46%.

$\text{Step 2: Using CAS}$

$\text{Next 3 years:}\ N=3 \times 12 = 36$

$\text{Minimum value of new payment}\ =$189.55$

$\Rightarrow A$

Financial Maths, GEN1 2024 VCAA 22-23 MC

Stewart takes out a reducing balance loan of \$240 000, with interest calculated monthly.

Stewart makes regular monthly repayments.

Three lines of the amortisation table are shown below.

\begin{array}{|c|r|r|r|r|}
\hline
\rule{0pt}{2.5ex} \textbf{Payment} & \textbf {Payment} & \textbf {Interest} &\textbf{Principal reduction} & \textbf{Balance}\\
\rule[-1ex]{0pt}{0pt}\textbf{number} & \textbf{($$$)}\ \ \ \ \ & \textbf{($$$)}\ \ \ \ \ & \textbf{($$$)}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ & \textbf{($$$)}\ \ \ \ \ \\
\hline
\rule{0pt}{2.5ex} 0 & 0.00 & 0.00 & 0.00\ \ \ \ \ \ \ \ \ \ & 240\,000.00 \\
\hline
\rule{0pt}{2.5ex} 1 & 2741.05 & 960.00 & 1781.05\ \ \ \ \ \ \ \ \ \ & 238\,218.95 \\
\hline
\rule{0pt}{2.5ex} 2 & 2741.05 & & & \\
\hline
\end{array}

Part 1

The principal reduction associated with Payment number 2 is closest to

$1773.93
$1781.05
$1788.17
$2741.05

Part 2

The number of years that it will take Stewart to repay the loan in full is closest to

Show Answers Only

Part 1: $C$

Part 2: $A$

Show Worked Solution

Part 1

$\text{Interest rate (monthly)}\ =\dfrac{960}{240\,000} = 0.004$

$\text{Interest repaid (payment 2)}\ =\dfrac{960}{240\,000}\times 238\,218.95=$952.88$

$\text{Principal Reduction (payment 2)}\ =2741.05-952.88=$1788.17$

$\Rightarrow C$

Part 2

$\text{Using CAS:}$

$\text{Annual interest rate}\ = 12 \times 0.004 = 4.8\%$

$\text{Number of repayments }= 108\ \text{months} = 9\ \text{years}$

$\Rightarrow A$

♦ Mean mark (Part 2) 54%.

Financial Maths, GEN1 2024 VCAA 20 MC

Dainika invested $2000 for three years at 4.4% per annum, compounding quarterly.

To earn the same amount of interest in three years in a simple interest account, the annual simple interest rate would need to be closest to

4.60%
4.68%
4.84%
4.98%

Show Answers Only

$B$

Show Worked Solution

$\text{Interest rate (per compounding period)} = \dfrac{4.4}{4} = 1.1 \%$

$\text{Compounding periods}\ =3\times4=12$

$FV=PV(1+r)^{n} = 2000(1+0.011)^{12}=$2280.57$

$\text{Annual interest}\ = \dfrac{280.57}{3}=$93.52$

$\text{S.I. rate}\ =\dfrac{93.52}{2000}\times 100\%=4.676\dots\%$

$\Rightarrow B$

♦ Mean mark 48%.

Recursion, GEN1 2024 VCAA 17 MC

A first-order linear recurrence relation of the form

$u_0=a, \quad \quad u_{n+1}=Ru_n+d$

generates the terms of a sequence. A geometric sequence will be generated if

$R=1$ and $d=-1$
$ R=1$ and $d=1$
$R=4$ and $d=-1$
$R=2$ and $d=0$

Show Answers Only

$D$

Show Worked Solution

$\text{Consider Option D where }R=2\ \text{and }d=0$

$u_0=a, \quad u_{n+1}=2u_n$

$\text{Generates the geometric sequence }\ a,\ 2a,\ 4a,\ 8a,\ …$

$\Rightarrow D$

♦♦ Mean mark 35%.

Data Analysis, GEN1 2024 VCAA 11-12 MC

The number of breeding pairs of a small parrot species has been declining over recent years.

The table below shows the number of breeding pairs counted, pairs, and the year number, year, for the last 12 years. A scatterplot of this data is also provided.

The association between pairs and year is non-linear.

Part 1

The scatterplot can be linearised using a logarithmic (base 10) transformation applied to the explanatory variable.

The least squares equation calculated from the transformed data is closest to

$\log _{10}(pairs)=2.44-0.0257 \times year$
$\log _{10}(pairs)=151-303 \times year$
$pairs =274-12.3 \times \log _{10}(year)$
$pairs =303-151 \times \log _{10}( year)$

Part 2

A reciprocal transformation applied to the variable $pairs$ can also be used to linearise the scatterplot.

When a least squares line is fitted to the plot of $\dfrac{1}{pairs}$ versus $year$, the largest difference between the actual value and the predicted value occurs at $year$

Show Answers Only

Part 1: $D$

Part 2: $A$

Show Worked Solution

Part 1

$\text{Apply reciprocal transformation and find regression line:}$

$\text{Least squares equation:}\ \ pairs=303-151\times\log_{10}{(year)}$

$\Rightarrow D$

Part 2

$\text{Largest difference occurs at year 1}$

$\Rightarrow A$

♦ Mean mark (Part 1) 48%.

Data Analysis, GEN1 2024 VCAA 9-10 MC

The least squares equation for the relationship between the average number of male athletes per competing nation, males, and the number of the Summer Olympic Games, number, is

$males =67.5-1.27 \times number$

Part 1

The summary statistics for the variables number and males are shown in the table below.

The value of Pearson's correlation coefficient, $r$, rounded to three decimal places, is closest to

$-0.569$
$-0.394$
$0.394$
$0.569$

Part 2

At which Summer Olympic Games will the predicted average number of males be closest to 25.6 ?

31st
32nd
33rd
34th

Show Answers Only

Part 1: $A$

Part 2: $C$

Show Worked Solution

Part 1

$b$	$=r \times \dfrac{s_y}{s_x}$
$-1.27$	$=r\times\dfrac{19}{8.51}$
$\therefore\ r$	$=\dfrac{-1.27\times 8.51}{19}$
	$=-0.5688\dots$

$\Rightarrow A$

♦ Mean mark (Part 1) 52%.

Part 2

$males$	$=67.5-1.27\times number$
$25.6$	$=67.5-1.27\times number$
$number$	$=\dfrac{67.5-25.6}{1.27}$
	$=32.992\dots$
	$\approx 33$

$\Rightarrow C$

Data Analysis, GEN1 2024 VCAA 6 MC

More than 11 000 athletes from more than 200 countries competed in the Tokyo Summer Olympic Games.

An analysis of the number of athletes per country produced the following five-number summary.

\begin{array}{|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} \textbf{Minimum} \rule[-1ex]{0pt}{0pt}& \textbf{First quartile } & \textbf{Median } & \textbf{Third quartile} & \textbf{Maximum } \\
\hline
\rule{0pt}{2.5ex} 2 \rule[-1ex]{0pt}{0pt}& 5 & 11 & 48 & 613 \\
\hline
\end{array}

The smallest number of athletes per country that would display as an outlier on a boxplot of this data is

Show Answers Only

$C$

Show Worked Solution

$IQR=48-5=43$

$\text{Upper boundary}$	$=Q_3+1.5\times IQR$
	$=48+1.5\times 43$
	$=112.5$

$\therefore\ \text{Smallest number of athletes to show as an outlier = 113.}$

$\Rightarrow C$

♦ Mean mark 53%.

Complex Numbers, EXT2 N2 2024 HSC 16b

The number $w=e^{\small{\dfrac{2 \pi i}{3}}}$ is a complex cube root of unity. The number $\gamma$ is a cube root of $w$.

Show that $\gamma+\bar{\gamma}$ is a real root of $z^3-3 z+1=0$. (3 marks)

--- 12 WORK AREA LINES (style=lined) ---
By using part (i) to find the exact value of $\cos \dfrac{2 \pi}{9} \cos \dfrac{4 \pi}{9} \cos \dfrac{8 \pi}{9}$, deduce the value(s) of $\cos \dfrac{2^n \pi}{9} \cos \dfrac{2^{n+1} \pi}{9} \cos \dfrac{2^{n+2} \pi}{9}$ for all integers $n \geq 1$. Justify your answer. (3 marks)

--- 12 WORK AREA LINES (style=lined) ---

Show Answers Only

i. $w=e^{\small{\dfrac{2 \pi i}{3}}} \Rightarrow \ \text{complex (cube) root of 1}$

$\gamma^3=w, \quad \gamma \bar{\gamma}=\abs{\gamma}^2=1$

$\text{Show}\ \ \gamma+\bar{\gamma}\ \ \text{is a real root of} \ \ z^3-3 z+1=0:$

	$(\gamma+\bar{\gamma})^3-3(\gamma+\bar{\gamma})+1$
		$=\gamma^3+3 \gamma^2 \bar{\gamma}+3 \gamma \bar{\gamma}^2+\bar{\gamma}^3-3 \gamma-3 \bar{\gamma}+1$
		$=\gamma^3+3 \gamma\abs{\gamma}^2+3 \bar{\gamma}\abs{\gamma}^2+\bar{\gamma}^3-3 \gamma-3 \bar{\gamma}+1$
		$=w+3 \gamma+3 \bar{\gamma}+\bar{w}-3 \gamma-3 \bar{\gamma}+1$
		$=w+\bar{w}+1$
		$=0 \quad \text{(Sum of complex roots of 1 = 0)}$

$\text{Show}\ \ \gamma+\bar{\gamma} \ \ \text{is real:}$

$\gamma+\bar{\gamma}=a+b i+a-b i=2 a \quad(a \in \mathbb{R})$

$\therefore \gamma+\bar{\gamma} \ \ \text{is a real root of} \ \ z^3-3 z+1=0.$

ii. $e^{\small{\dfrac{2 \pi i}{9}}}\ \ \text{is a cube root of}\ \ \omega \ \Rightarrow \ \Bigg(e^{\small{\dfrac{2 \pi i}{9}}}\Bigg)^3=e^{\small{\dfrac{2 \pi i}{3}}}$

$\text{Cubic roots are} \ \dfrac{2}{3} \ \text {rotations from each other.}$

$\text{Roots of} \ \ z^3-3 z+1=0:$

	$(\gamma+\bar{\gamma})_1$	$=2 \cos \left(\dfrac{2 \pi}{9}\right)$
	$(\gamma+\bar{\gamma})_2$	$=2 \cos \left(\dfrac{8 \pi}{9}\right)$
	$(\gamma+\bar{\gamma})_3$	$=2 \cos \left(\dfrac{4\pi}{9}\right)$

$\text{Product of roots} \ \ \alpha B \gamma=-\dfrac{d}{a}:$

	$2 \cos \left(\dfrac{2 \pi}{9}\right) \cdot 2 \cos \left(\dfrac{8 \pi}{9}\right) \cdot 2 \cos \left(\dfrac{4 \pi}{4}\right)$	$=-1$
	$\cos \left(\dfrac{2 \pi}{9}\right) \cdot \cos \left(\dfrac{8 \pi}{9}\right) \cdot \cos \left(\dfrac{4 \pi}{9}\right)$	$=-\dfrac{1}{8}$

$\text{Consider} \ \ \cos \left(\dfrac{2 \pi}{9}\right) \cdot \cos \left(\dfrac{2^{n+1} \pi}{9}\right) \cdot \cos \left(\dfrac{2^{n+2} \pi}{9}\right):$

$\text{If} \ \ n=1,$

$\cos \left(\dfrac{2 \pi}{9}\right) \cdot \cos \left(\dfrac{4 \pi}{9}\right) \cdot \cos \left(\dfrac{8 \pi}{9}\right)=-\dfrac{1}{8}\ \ \text{(see above)}$

$\text {If} \ \ n=2,$

$\cos \left(\dfrac{4 \pi}{9}\right) \cdot \cos \left(\dfrac{8 \pi}{9}\right) \cdot \cos \left(\dfrac{2\pi}{9}\right)=-\dfrac{1}{8}$

$\Rightarrow \ \text{Multiplying each argument by 2 does not change the equation}$

$\therefore \cos \left(\dfrac{2^n \pi}{9}\right) \cdot \cos \left(\dfrac{2^{n+1} \pi}{9}\right) \cdot \cos \left(\dfrac{2^{n+2} \pi}{9}\right)=-\dfrac{1}{8}$

Show Worked Solution

i. $w=e^{\small{\dfrac{2 \pi i}{3}}} \Rightarrow \ \text{complex (cube) root of 1}$

$\gamma^3=w, \quad \gamma \bar{\gamma}=\abs{\gamma}^2=1$

$\text{Show}\ \ \gamma+\bar{\gamma}\ \ \text{is a real root of} \ \ z^3-3 z+1=0:$

♦♦ Mean mark (i) 36%.

	$(\gamma+\bar{\gamma})^3-3(\gamma+\bar{\gamma})+1$
		$=\gamma^3+3 \gamma^2 \bar{\gamma}+3 \gamma \bar{\gamma}^2+\bar{\gamma}^3-3 \gamma-3 \bar{\gamma}+1$
		$=\gamma^3+3 \gamma\abs{\gamma}^2+3 \bar{\gamma}\abs{\gamma}^2+\bar{\gamma}^3-3 \gamma-3 \bar{\gamma}+1$
		$=w+3 \gamma+3 \bar{\gamma}+\bar{w}-3 \gamma-3 \bar{\gamma}+1$
		$=w+\bar{w}+1$
		$=0 \quad \text{(Sum of complex roots of 1 = 0)}$

$\text{Show}\ \ \gamma+\bar{\gamma} \ \ \text{is real:}$

$\gamma+\bar{\gamma}=a+b i+a-b i=2 a \quad(a \in \mathbb{R})$

$\therefore \gamma+\bar{\gamma} \ \ \text{is a real root of} \ \ z^3-3 z+1=0.$

ii. $e^{\small{\dfrac{2 \pi i}{9}}}\ \ \text{is a cube root of}\ \ \omega \ \Rightarrow \ \Bigg(e^{\small{\dfrac{2 \pi i}{9}}}\Bigg)^3=e^{\small{\dfrac{2 \pi i}{3}}}$

$\text{Cubic roots are} \ \dfrac{2}{3} \ \text {rotations from each other.}$

♦♦♦ Mean mark (ii) 18%.

$\text{Roots of} \ \ z^3-3 z+1=0:$

	$(\gamma+\bar{\gamma})_1$	$=2 \cos \left(\dfrac{2 \pi}{9}\right)$
	$(\gamma+\bar{\gamma})_2$	$=2 \cos \left(\dfrac{8 \pi}{9}\right)$
	$(\gamma+\bar{\gamma})_3$	$=2 \cos \left(\dfrac{4\pi}{9}\right)$

$\text{Product of roots} \ \ \alpha B \gamma=-\dfrac{d}{a}:$

	$2 \cos \left(\dfrac{2 \pi}{9}\right) \cdot 2 \cos \left(\dfrac{8 \pi}{9}\right) \cdot 2 \cos \left(\dfrac{4 \pi}{4}\right)$	$=-1$
	$\cos \left(\dfrac{2 \pi}{9}\right) \cdot \cos \left(\dfrac{8 \pi}{9}\right) \cdot \cos \left(\dfrac{4 \pi}{9}\right)$	$=-\dfrac{1}{8}$

$\text{Consider} \ \ \cos \left(\dfrac{2 \pi}{9}\right) \cdot \cos \left(\dfrac{2^{n+1} \pi}{9}\right) \cdot \cos \left(\dfrac{2^{n+2} \pi}{9}\right):$

$\text{If} \ \ n=1,$

$\cos \left(\dfrac{2 \pi}{9}\right) \cdot \cos \left(\dfrac{4 \pi}{9}\right) \cdot \cos \left(\dfrac{8 \pi}{9}\right)=-\dfrac{1}{8}\ \ \text{(see above)}$

$\text {If} \ \ n=2,$

$\cos \left(\dfrac{4 \pi}{9}\right) \cdot \cos \left(\dfrac{8 \pi}{9}\right) \cdot \cos \left(\dfrac{2\pi}{9}\right)=-\dfrac{1}{8}$

$\Rightarrow \ \text{Multiplying each argument by 2 does not change the equation}$

$\therefore \cos \left(\dfrac{2^n \pi}{9}\right) \cdot \cos \left(\dfrac{2^{n+1} \pi}{9}\right) \cdot \cos \left(\dfrac{2^{n+2} \pi}{9}\right)=-\dfrac{1}{8}$

Calculus, EXT2 C1 2024 HSC 15d

Using a suitable substitution, find $\displaystyle\int \dfrac{2 x^2}{\sqrt{2 x-x^2}}\, d x$. (3 marks)

--- 12 WORK AREA LINES (style=lined) ---

Show Answers Only

$I=3 \sin ^{-1}(x-1)-4 \sqrt{2x-x^2}-(x-1) \sqrt{2x-x^2}+c$

Show Worked Solution

	$\displaystyle \int \dfrac{2x^2}{\sqrt{2x-x^2}}\, dx$	$=\displaystyle \int \frac{2 x^2}{\sqrt{1-(1-2 x+x^2)}}\, dx$
		$=\displaystyle \int \frac{2 x^2}{\sqrt{1-(x-1)^2}} \, dx$

♦ Mean mark 49%.

$\text {Let} \ \ x-1=\sin \theta \ \Rightarrow \ x=1+\sin \theta$

$\dfrac{dx}{d \theta}=\cos \theta \ \Rightarrow \ dx=\cos \theta \, d \theta$

	$I$	$=\displaystyle \int \frac{2(1+\sin \theta)^2}{\sqrt{1-\sin ^2 \theta}} \cdot \cos \theta \, d \theta$
		$=2 \displaystyle \int \frac{1+2 \sin \theta+\sin ^2 \theta}{\cos \theta} \cdot \cos \theta \, d \theta$
		$=2 \displaystyle \int 1+2 \sin \theta+\frac{1}{2}(1-\cos (2 \theta)) \, d \theta$
		$=\displaystyle \int 2+4 \sin \theta+1-\cos (2 \theta) \, d \theta$
		$=\displaystyle \int 3+4 \sin \theta-\cos (2 \theta) \, d \theta$
		$=3 \theta-4 \cos \theta-\dfrac{1}{2} \sin (2 \theta)+c$
		$=3 \theta-4 \cos \theta-\sin \theta \cos \theta+c$

$\Rightarrow \cos \theta=\sqrt{1^2-(x-1)^2}=\sqrt{2x-x^2}$

$\therefore I=3 \sin ^{-1}(x-1)-4 \sqrt{2x-x^2}-(x-1) \sqrt{2x-x^2}+c$

Vectors, EXT2 V1 2024 HSC 14e

The diagram shows triangle $O Q A$.

The point $P$ lies on $O A$ so that $O P: O A=3: 5$.

The point $B$ lies on $O Q$ so that $O B: O Q=1: 3$.

The point $R$ is the intersection of $A B$ and $P Q$.

The point $T$ is chosen on $A Q$ so that $O, R$ and $T$ are collinear.

Let $\underset{\sim}{a}=\overrightarrow{O A}, \ \underset{\sim}{b}=\overrightarrow{O B}$ and $\overrightarrow{P R}=k \overrightarrow{P Q}$ where $k$ is a real number.

Show that $\overrightarrow{O R}=\dfrac{3}{5}(1-k) \underset{\sim}{a}+3 k \underset{\sim}{b}$. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Writing $\overrightarrow{A R}=h \overrightarrow{A B}$, where $h$ is a real number, it can be shown that $\overrightarrow{O R}=(1-h) \underset{\sim}{a}+h \underset{\sim}{b}$. (Do NOT prove this.)

Show that $k=\dfrac{1}{6}$. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Find $\overrightarrow{O T}$ in terms of $\underset{\sim}{a}$ and $\underset{\sim}{b}$. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

i. $\underset{\sim}{a}=\overrightarrow{O A}, \ \underset{\sim}{b}=\overrightarrow{O B}, \ \overrightarrow{P R}=k \overrightarrow{P Q}$

$\overrightarrow{O P}: \overrightarrow{O A}=3: 5 \ \Rightarrow \ \overrightarrow{O P} = \dfrac{3}{5} \times \overrightarrow{O A} $

$\overrightarrow{O B}: \overrightarrow{O Q}=1: 3\ \Rightarrow \ \overrightarrow{O Q} = 3 \times \overrightarrow{OB} $

$\text {Show } \overrightarrow{O R}=\dfrac{3}{5}(1-k) \underset{\sim}{a}+3 k \underset{\sim}{b}$

	$\overrightarrow{O R}$	$=\overrightarrow{O P}+k \overrightarrow{P Q}$
		$=\overrightarrow{O P}+k(\overrightarrow{O Q}-\overrightarrow{O P})$
		$=(1-k) \overrightarrow{O P}+k \overrightarrow{O Q}$
		$=\dfrac{3}{5}(1-k)\underset{\sim}{a}+3 k \underset{\sim}{b}$

ii. $\overrightarrow{A R}=h \overrightarrow{A B}, \quad h \in \mathbb{R}$

$\overrightarrow{OR}=(1-h) \underset{\sim}{a}+h \underset{\sim}{b} \ \ \text{(given)}$

$\overrightarrow{O R}=\dfrac{3}{5}(1-k) \underset{\sim}{a}+3 k \underset{\sim}{b} \ \ \text{(part(i))}$

$\text{Vector }\underset{\sim}{a} \neq \lambda \underset{\sim}{b}\ (\lambda \in \mathbb{R})\ \Rightarrow \ \text{linearly independent and are basis vectors for } \overrightarrow{O R}$.

$\text {Equating coefficients:}$

$\dfrac{3}{5}(1-k)=1-h\ \ldots\ (1)$

$h=3 k\ \ldots\ (2)$

$\text{Substituting (2) into (1)}$

	$\dfrac{3}{5}(1-k)$	$=1-3 k$
	$3-3 k$	$=5-15 k$
	$k$	$=\dfrac{1}{6}$

iii. $\overrightarrow{O T}=\dfrac{3}{4}(\underset{\sim}{a}+\underset{\sim}{b})$

Show Worked Solution

i. $\underset{\sim}{a}=\overrightarrow{O A}, \ \underset{\sim}{b}=\overrightarrow{O B}, \ \overrightarrow{P R}=k \overrightarrow{P Q}$

$\overrightarrow{O P}: \overrightarrow{O A}=3: 5 \ \Rightarrow \ \overrightarrow{O P} = \dfrac{3}{5} \times \overrightarrow{O A} $

$\overrightarrow{O B}: \overrightarrow{O Q}=1: 3\ \Rightarrow \ \overrightarrow{O Q} = 3 \times \overrightarrow{OB} $

$\text {Show } \overrightarrow{O R}=\dfrac{3}{5}(1-k) \underset{\sim}{a}+3 k \underset{\sim}{b}$

	$\overrightarrow{O R}$	$=\overrightarrow{O P}+k \overrightarrow{P Q}$
		$=\overrightarrow{O P}+k(\overrightarrow{O Q}-\overrightarrow{O P})$
		$=(1-k) \overrightarrow{O P}+k \overrightarrow{O Q}$
		$=\dfrac{3}{5}(1-k)\underset{\sim}{a}+3 k \underset{\sim}{b}$

ii. $\overrightarrow{A R}=h \overrightarrow{A B}, \quad h \in \mathbb{R}$

$\overrightarrow{OR}=(1-h) \underset{\sim}{a}+h \underset{\sim}{b} \ \ \text{(given)}$

$\overrightarrow{O R}=\dfrac{3}{5}(1-k) \underset{\sim}{a}+3 k \underset{\sim}{b} \ \ \text{(part(i))}$

$\text{Vector }\underset{\sim}{a} \neq \lambda \underset{\sim}{b}\ (\lambda \in \mathbb{R})\ \Rightarrow \ \text{linearly independent and are basis vectors for } \overrightarrow{O R}$.

$\text {Equating coefficients:}$

$\dfrac{3}{5}(1-k)=1-h\ \ldots\ (1)$

$h=3 k\ \ldots\ (2)$

$\text{Substituting (2) into (1)}$

	$\dfrac{3}{5}(1-k)$	$=1-3 k$
	$3-3 k$	$=5-15 k$
	$k$	$=\dfrac{1}{6}$

iii. $\overrightarrow{O T}=\lambda \overrightarrow{O R}$

$\text {Using parts (i) and (ii):}$

$\overrightarrow{O R}=\dfrac{3}{5}\left(1-\dfrac{1}{6}\right)\underset{\sim}{a}+3\left(\dfrac{1}{6}\right) \underset{\sim}{b}=\dfrac{1}{2}\left(\underset{\sim}{a}+\underset{\sim}{b}\right)$

$\overrightarrow{O T}=\dfrac{\lambda}{2}(\underset{\sim}{a}+\underset{\sim}{b})$

♦ Mean mark (iii) 45%.

$\text {Find } \lambda:$

	$\overrightarrow{O T}$	$=\overrightarrow{O A}+\mu \overrightarrow{A Q}$
	$\dfrac{\lambda}{2}(\underset{\sim}{a}+\underset{\sim}{b})$	$=\underset{\sim}{a}+\mu(3 \underset{\sim}{b}-\underset{\sim}{a}) \quad \Big(\text{noting}\ \overrightarrow{A Q}=\overrightarrow{O Q}-\overrightarrow{O A}=3 \underset{\sim}{b}-\underset{\sim}{a}\Big)$
		$=\underset{\sim}{a}(1-\mu)+3 \mu \underset{\sim}{b}$

$\text {Equating coefficients:}$

$\dfrac{\lambda}{2}=3 \mu \ \Rightarrow \ \mu=\dfrac{\lambda}{6}$

	$1-\dfrac{\lambda}{6}$	$=\dfrac{\lambda}{2}$
	$6-\lambda$	$=3 \lambda$
	$\lambda$	$=\dfrac{3}{2}$

$\therefore \overrightarrow{O T}=\dfrac{3}{4}(\underset{\sim}{a}+\underset{\sim}{b})$

Complex Numbers, EXT2 N2 2024 HSC 14c

For the complex numbers $z$ and $w$, it is known that $\arg \left(\dfrac{z}{w}\right)=-\dfrac{\pi}{2}$.

Find $\left|\dfrac{z-w}{z+w}\right|$. (2 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

$\abs{\dfrac{z-w}{z+w}}=1$

Show Worked Solution

$\arg \left(\dfrac{z}{w}\right)=\arg \, z-\arg \, w=-\dfrac{\pi}{2}$

$\text{Graphically, \(\arg \, z$ is a $90^{\circ}$ anticlockwise rotation from $\arg \, w$.}\)

♦ Mean mark 49%.

$\abs{z-w}=\abs{z+w} \ \text{(diagonals of rectangle)}$

$\therefore \abs{\dfrac{z-w}{z+w}}=1$

Proof, EXT2 P1 2024 HSC 14d

The following argument attempts to prove that $0=1$.

We evaluate $\displaystyle\int \frac{1}{x}\, d x$ using the method of integration by parts.

	$\displaystyle \int \frac{1}{x}\,d x$	$=\displaystyle \int \frac{1}{x} \times 1\, d x$
		$=\displaystyle\frac{1}{x} \times x-\int-\frac{1}{x^2} x\, d x$
		$=1+\displaystyle\int \frac{1}{x}\, d x$

We may now subtract $\displaystyle \int \frac{1}{x}\,d x$ from both sides to show that $0=1$.

Explain what is wrong with this argument. (2 marks)

--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text {Consider the line in proof }$

$\displaystyle {\int \frac{1}{x}\, d x=1+\int \frac{1}{x}\, d x}$

$\Rightarrow \text{ Each integral will have its own constant }$

$\Rightarrow \text{If constants are \(c_1$ and $c_2, \abs{c_1-c_2}=1$ in this proof.}\)

$\Rightarrow \text{Subtracting}\ \displaystyle \int \frac{1}{x}\,d x\ \text{from both sides invalidates the proof.}$

Show Worked Solution

$\text {Consider the line in proof }$

$\displaystyle {\int \frac{1}{x}\, d x=1+\int \frac{1}{x}\, d x}$

♦♦ Mean mark 34%.

$\Rightarrow \text{ Each integral will have its own constant }$

$\Rightarrow \text{If constants are \(c_1$ and $c_2, \abs{c_1-c_2}=1$ in this proof.}\)

$\Rightarrow \text{Subtracting}\ \displaystyle \int \frac{1}{x}\,d x\ \text{from both sides invalidates the proof.}$

Vectors, EXT2 V1 2024 HSC 13a

The point $A$ has position vector $8 \underset{\sim}{i}-6 \underset{\sim}{j}+5 \underset{\sim}{k}$. The line $\ell$ has vector equation

$x \underset{\sim}{i}+y \underset{\sim}{j}+z \underset{\sim}{k}=t(\underset{\sim}{i}+\underset{\sim}{j}+2 \underset{\sim}{k})$.

The point $B$ lies on $\ell$ and has position vector $p \underset{\sim}{i}+p \underset{\sim}{j}+2 p \underset{\sim}{k}$.

Show that $\abs{A B}^2=6 p^2-24 p+125$. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---
Hence, or otherwise, determine the shortest distance between the point $A$ and the line $\ell$. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

i. $A\left(\begin{array}{c}8 \\ -6 \\ 5\end{array}\right), \quad \ell: \left(\begin{array}{l}x \\ y \\ z\end{array}\right)+t\left(\begin{array}{l}1 \\ 1 \\ 2\end{array}\right), \quad B\left(\begin{array}{c}p \\ p \\ 2 p\end{array}\right)$

$\overrightarrow{A B}=\left(\begin{array}{l}p \\ p \\ 2 p\end{array}\right)-\left(\begin{array}{c}8 \\ -6 \\ 5\end{array}\right)=\left(\begin{array}{c}p-8 \\ p+6 \\ 2 p-5\end{array}\right)$

	$\abs{AB}^2$	$=(p-8)^2+(p+6)^2+(2 p-5)^2$
		$=p^2-16 p+64+p^2+12 p+36+4 p^2-20 p+25$
		$=6 p^2-24 p+125$

ii. $\abs{AB}_{\text {min}}=\sqrt{101} \text { units}$

Show Worked Solution

$\overrightarrow{A B}=\left(\begin{array}{l}p \\ p \\ 2 p\end{array}\right)-\left(\begin{array}{c}8 \\ -6 \\ 5\end{array}\right)=\left(\begin{array}{c}p-8 \\ p+6 \\ 2 p-5\end{array}\right)$

	$\abs{AB}^2$	$=(p-8)^2+(p+6)^2+(2 p-5)^2$
		$=p^2-16 p+64+p^2+12 p+36+4 p^2-20 p+25$
		$=6 p^2-24 p+125$

ii. $\text{Find shortest distance between \(A$ and $\ell$.}\)

$\Rightarrow \text { Find \(p$ when $\abs{A B}$ is a minimum:}\)

$\text{Minimum occurs when}\ \ p=\dfrac{-b}{2 a}=\dfrac{24}{2 \times 6}=2$

$\therefore \abs{AB}_{\text {min}}=\sqrt{6(2)^2-24(2)+125}=\sqrt{101} \text { units}$

♦ Mean mark (ii) 45%.

Proof, EXT2 P1 2024 HSC 12d

Explain why there is no integer $n$ such that $(n+1)^{41}-79 n^{40}=2$. (2 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{Show}\ \ \nexists \, n \in \mathbb{Z}: \ (n+1)^{41}-79 n^{40}=2$

$\text {If \(n$ is even:}\)

$\text{LHS}=(\text{odd})^{41}-79(\text{even})^{40}=\text {odd}-\text {even}=\text {odd} \neq 2$

$\text {If \(n$ is odd:}\)

$\text {LHS }=(\text {even})^{41}-79(\text {odd})^{40}=\text {even}- \text {odd}=\text {odd} \neq 2$

$\therefore\ \text {By contradiction}$

$\nexists \, n \in \mathbb{Z}: \ (n+1)^{41}-79 n^{40}=2$

Show Worked Solution

$\text{Show}\ \ \nexists \, n \in \mathbb{Z}: \ (n+1)^{41}-79 n^{40}=2$

$\text {If \(n$ is even:}\)

$\text{LHS}=(\text{odd})^{41}-79(\text{even})^{40}=\text {odd}-\text {even}=\text {odd} \neq 2$

$\text {If \(n$ is odd:}\)

$\text {LHS }=(\text {even})^{41}-79(\text {odd})^{40}=\text {even}- \text {odd}=\text {odd} \neq 2$

$\therefore\ \text {By contradiction}$

$\nexists \, n \in \mathbb{Z}: \ (n+1)^{41}-79 n^{40}=2$

♦ Mean mark 49%.

Trigonometry, EXT1 T3 2024 HSC 14c

Explain why the equation $\tan ^{-1}(3 x)+\tan ^{-1}(10 x)=\theta$, where $-\pi<\theta<\pi$, has exactly one solution. (1 marks)

--- 5 WORK AREA LINES (style=lined) ---
Solve $\tan ^{-1}(3 x)+\tan ^{-1}(10 x)=\dfrac{3 \pi}{4}$. (2 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

i. $\tan ^{-1}(3 x)+\tan ^{-1}(10 x)=\theta \quad-\pi<\theta<\pi$

$\text {Range:}\ \ \tan ^{-1}(3 x) \in\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right), \ \tan ^{-1}(10 x) \in\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)$

$\Rightarrow \text { Both are monotonically increasing functions}$

$\Rightarrow\tan ^{-1}(3 x)+\tan ^{-1}(10 x) \text{ is also monotonically increasing with range }(-\pi, \pi)$

$\Rightarrow \text{ Only 1 solution exists (horizontal line will only cut graph once).}$

ii. $x=\dfrac{1}{2}$

Show Worked Solution

i. $\tan ^{-1}(3 x)+\tan ^{-1}(10 x)=\theta \quad-\pi<\theta<\pi$

$\text {Range:}\ \ \tan ^{-1}(3 x) \in\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right), \ \tan ^{-1}(10 x) \in\left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right)$

♦♦♦ Mean mark (i) 11%.

$\Rightarrow \text { Both are monotonically increasing functions}$

$\Rightarrow\tan ^{-1}(3 x)+\tan ^{-1}(10 x) \text{ is also monotonically increasing with range }(-\pi, \pi)$

$\Rightarrow \text{ Only 1 solution exists (horizontal line will only cut graph once).}$

ii. $\tan ^{-1}(3 x)+\tan ^{-1}(10 x)=\dfrac{3 \pi}{4}$

$\tan \left(\tan ^{-1}(3 x)+\tan ^{-1}(10 x)\right)=\tan \left(\dfrac{3 \pi}{4}\right)$

♦♦ Mean mark (ii) 32%.

$\dfrac{\tan \left(\tan ^{-1}(3 x)\right)+\tan \left(\tan ^{-1}(10 x)\right)}{1-\tan \left(\tan ^{-1}(3 x)\right) \cdot \tan \left(\tan ^{-1}(10 x)\right)}=-1$

	$\dfrac{3 x+10 x}{1-30 x^2}$	$=-1$
	$13 x$	$=30 x^2-1$
	$30 x^2-13 x-1$	$=0$
	$(15 x+1)(2 x-1)$	$=0$

$x=\dfrac{1}{2}\ \ \text {or}\ \ -\dfrac{1}{15}$

$\text {Graph is monotonically increasing through } (0,0) \Rightarrow \ \Big(x \neq -\dfrac{1}{15} \Big)$

$\therefore x=\dfrac{1}{2}$

Calculus, EXT1 C2 2024 HSC 14b

For what values of the constant $k$ would the function $f(x)=\dfrac{k x}{1+x^2}+\arctan x$ have an inverse? (3 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

$f(x)\ \text{has an inverse for}\ \ -1 \leqslant k \leqslant 1$

Show Worked Solution

	$f(x)$	$=\dfrac{k x}{1+x^2}+\arctan x$
	$f^{\prime}(x)$	$=\dfrac{k\left(1+x^2\right)-k x(2 x)}{\left(1+x^2\right)^2}+\dfrac{1}{1+x^2}$
		$=\dfrac{k+k x^2-2 k x^2+1+x^2}{\left(1+x^2\right)^2}$
		$=\dfrac{x^2(1-k)+k+1}{\left(1+x^2\right)^2}$

♦♦♦ Mean mark 26%.

$\text{Inverse function } \Rightarrow f(x) \text { has no SPs}$

$x^2(1-k)+k+1 \neq 0$

$\text {No solution if } \ \Delta<0:$

	$-4(1-k)(k+1)$	$<0$
	$(1-k)(k+1)$	$>0$

$f(x)\ \text{has an inverse for}\ \ -1 \leq k \leq 1$

Calculus, EXT1 C3 2024 HSC 14a

Find the domain and range of the function that is the solution to the differential equation

$\dfrac{d y}{d x}=e^{x+y}$

and whose graph passes through the origin. (4 marks)

--- 9 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{Domain:}\ \ x<\ln 2$

$\text{Range:}\ \ y>-\ln 2$

Show Worked Solution

$\dfrac{d y}{d x}=e^{x+y}=e^{x}\cdot e^{y}$

	$\displaystyle\int e^{-y}\, d y$	$=\displaystyle \int e^x\, d x$
	$-e^{-y}$	$=e^x+c$

♦ Mean mark 52%.

$\text{Passes through }(0,0):$

$-e^0=e^0+c \ \Rightarrow \ c=-2$

	$-e^{-y}$	$=e^x-2$
	$e^{-y}$	$=2-e^x$
	$-y$	$=\ln \left(2-e^x\right)$
	$y$	$=-\ln \left(2-e^x\right)$

$\text{Since}\ \ 2-e^x>0 \ \Rightarrow \ e^x<2$

$\Rightarrow \ \text{Domain:}\ \ x<\ln 2$

$\text{Since}\ \ e^x>0 \ \Rightarrow \ 2-e^x<2$

$\Rightarrow \ \text{Range:}\ \ y>-\ln 2$

Vectors, EXT1 V1 2024 HSC 13c

The vector $\underset{\sim}{a}$ is $\displaystyle \binom{1}{3}$ and the vector $\underset{\sim}{b}$ is $\displaystyle\binom{2}{-1}$.

The projection of a vector $\underset{\sim}{x}$ onto the vector $\underset{\sim}{a}$ is $k \underset{\sim}{a}$, where $k$ is a real number.

The projection of the vector $\underset{\sim}{x}$ onto the vector $\underset{\sim}{b}$ is $p \underset{\sim}{b}$, where $p$ is a real number.

Find the vector $\underset{\sim}{x}$ in terms of $k$ and $p$. (4 marks)

--- 12 WORK AREA LINES (style=lined) ---

Show Answers Only

$\underset{\sim}{x}=\dfrac{5}{7} \displaystyle \binom{2 k+3 p}{4 k-p}$

Show Worked Solution

$\underset{\sim}{a}=\displaystyle \binom{1}{3}, \ \abs{\underset{\sim}{a}}=\sqrt{1^2+3^2}=\sqrt{10}$

$\underset{\sim}{b}=\displaystyle \binom{2}{-1}, \ \abs{\underset{\sim}{b}}=\sqrt{2^2+(-1)^2}=\sqrt{5}$

$\text{Let } \underset{\sim}{x}=\displaystyle \binom{x_1}{x_2}$

$\operatorname{proj}_{\underset{\sim}{a}} \underset{\sim}{x}=\dfrac{\underset{\sim}{x} \cdot \underset{\sim}{a}}{|\underset{\sim}{a}|^2} \underset{\sim}{a}=\dfrac{x_1+3 x_2}{10} \cdot \underset{\sim}{a}$

$k=\dfrac{x_1+3 x_2}{10} \ \Rightarrow \ x_1+3 x_2=10 k\ \ldots\ (1)$

♦ Mean mark 47%.

$\operatorname{proj}_{\underset{\sim}{b}} \underset{\sim}{x}=\dfrac{\underset{\sim}{b} \cdot \underset{\sim}{x}}{|\underset{\sim}{b}|^2} b=\dfrac{2 x_1-x_2}{5} \cdot \underset{\sim}{b}$

$p=\dfrac{2 x_1-x_2}{5} \ \Rightarrow \ 2 x_1-x_2=5 p\ \ldots\\ (2)$

$\text {Multiply } (2) \times 3$

$6 x_1-3 x_2=15 p\ \ldots\ (3)$

$(1)+(3)$

$7 x_1$	$=10 k+15 p$
$x_1$	$=\dfrac{1}{7}(10 k+15)$

$\text {Multiply } (1) \times 2$

$2 x_1+6 x_2=20 k\ \ldots\ (4)$

$\text {Subtract} (4)-(2)$

$7x_2$	$=20 k-5 p$
$x_2$	$=\dfrac{1}{7}(20 k-5 p)$

$\therefore \underset{\sim}{x}=\displaystyle \frac{1}{7}\binom{10 k+15 p}{20 k-5 p}=\frac{5}{7}\binom{2 k+3 p}{4 k-p}$

Calculus, EXT1 C3 2024 HSC 13a

In an experiment, the population of insects, $P(t)$, was modelled by the logistic differential equation

$\dfrac{d P}{d t}=P(2000-P)$

where $t$ is the time in days after the beginning of the experiment.

The diagram shows a direction field for this differential equation, with the point $S$ representing the initial population.

Explain why the graph of the solution that passes through the point $S$ cannot also pass through the point $T$. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Clearly sketch the graph of the solution that passes through the point $S$. (1 mark)

--- 5 WORK AREA LINES (style=blank) ---
Find the predicted value of the population, $P(t)$, at which the rate of growth of the population is largest. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

i. $\text{Any solution that passes through}\ S\ \text{will follow the}$

$\text{slope field (not crossing any lines) and approach a horizontal}$

$\text{asymptote at}\ P=2000\ \text{from the lower side}\ (P<2000).$

ii.

iii. $P= 1000$

Show Worked Solution

i. $\text{Any solution that passes through}\ S\ \text{will follow the}$

$\text{slope field (not crossing any lines) and approach a horizontal}$

$\text{asymptote at}\ P=2000\ \text{from the lower side}\ (P<2000).$

ii.

iii. $\dfrac{d P}{d t}=P(2000-P)$

$\text {Find \(P$ where $\dfrac{d P}{d t}$ is a maximum.}\)

$\text{Consider the graph}\ \ y=P(2000-P): $

$\Rightarrow \ \text {Graph is a concave down quadratic cutting at}\ \ P=0\ \ \text{and}\ \ P=2000$

$\Rightarrow \ \text{Max value of}\ \ P(2000-P)\ \ \Big(\text{i.e.}\ \dfrac{dP}{dt}\Big)\ \ \text{occurs at}\ \ P=1000\ \text{(axis).}$

♦ Mean mark (iii) 51%.

CHEMISTRY, M2 EQ-Bank 14

The concentration of a solution of hydrochloric acid $\ce{HCl}$ is 1.80% (w/v). What is the molar concentration produced by diluting 20.0 mL of this solution to a total volume of 200.0 mL with deionised water? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

$0.049\ \text{mol/L}$

Show Worked Solution

1.8% (w/v) means that there is 1.8 g of solute in 100 mL.
In 20 mL, there is $1.8\ \text{g} \times 0.2 = 0.36\ \text{g}$ of $\ce{HCl}$.
$n\ce{(HCl)} = \dfrac{0.36}{1.008 + 35.45} = 0.00987\ \text{mol}$
The final concentration after the dilution will be:
$c = \dfrac{n}{V} = \dfrac{0.00987}{0.2} = 0.049\ \text{mol/L}$

CHEMISTRY, M2 EQ-Bank 13

Calculate the volume of solution needed to obtain 0.6 moles of solute from a solution of concentration 1.2 mol/L. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---

Explain the significance of accurate volume measurements when preparing solutions of specific concentrations in the laboratory. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $0.5\ \text{L}$

b. The exact volumes of solutions must be known as:

The concentration of each solution must be precise, as it affects the molar ratios and yields.
Miscalculating volume would lead to incorrect concentrations, impacting experimental results and validity.

Show Worked Solution

a. $V=\dfrac{n}{c}=\dfrac{0.6}{1.2}=0.5\ \text{L}$

b. The exact volumes of solutions must be known as:

The concentration of each solution must be precise, as it affects the molar ratios and yields.
Miscalculating volume would lead to incorrect concentrations, impacting experimental results and validity.

Statistics, EXT1 S1 2024 HSC 9 MC

A bag contains $n$ metal coins, $n \ge 3$, that are made from either silver or bronze.

There are $k$ silver coins in the bag and the rest are bronze.

Two coins are to be drawn at random from the bag, with the first coin drawn not being replaced before the second coin is drawn.

Which of the following expressions will give the probability that the two coins drawn are made of the same metal?

$\dfrac{k(k-1)+(n-k)(n-k-1)}{n(n-1)}$
$\left(\begin{array}{l}n \\ 2\end{array}\right) \left(\begin{array}{l}n \\ k\end{array}\right) \left(\begin{array}{l}1-\dfrac{k}{n} \end{array}\right)^{n-2} $
$\dfrac{\left(\begin{array}{l}k \\ 2\end{array}\right) + \left(\begin{array}{c}n-k \\ 2\end{array}\right)}{n(n-1)} $
$\dfrac{k^{2}+(n-k)^2}{n^{2}}$

Show Answers Only

$A$

Show Worked Solution

$P(B)=P(\text{Bronze}), \ P(S)=P(\text{Silver}) $

$n=\ \text{total coins},\ k=\ \text{bronze coins},\ n-k=\ \text{silver coins}$

$P(BB \cup SS)$	$=\dfrac{k}{n} \times \dfrac{k-1}{n-1} + \dfrac{n-k}{n} \times \dfrac{n-k-1}{n-1}$
	$=\dfrac{k(k-1)+(n-k)(n-k-1)}{n(n-1)}$

$\Rightarrow A$

♦ Mean mark 54%.

CHEMISTRY, M2 EQ-Bank 11

A student is investigating the concentration of copper ions in a water sample collected from a local river. They use an instrument to determine that the sample contains copper ions at a concentration level of 1.75 ppm.

Calculate the mass of copper ions in a 2 L sample of water. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Explain why parts per million is a suitable unit for measuring low concentrations of ions in environmental samples like river water. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. 3.5 mg

b. Benefits of using ppm as a concentration measurement.

Parts per million (ppm) is suitable for measuring low concentrations of ions because it represents the mass of solute per million parts of solution, making it ideal for detecting trace levels of substances.
This unit allows for easy comparison of small concentrations, which is especially useful in environmental studies where contaminants are present in very low amounts.

Show Worked Solution

a. $1\ \text{ppm} = 1\ \text{mg/L}$

$\Rightarrow \ce{[Cu^{2+}]} = 1.75\ \text{mg/L}$

$m\ce{(Cu^{2+})} = 1.75 \times 2 = 3.5\ \text{mg}$

b. Benefits of using ppm as a concentration measurement.

Parts per million (ppm) is suitable for measuring low concentrations of ions because it represents the mass of solute per million parts of solution, making it ideal for detecting trace levels of substances.
This unit allows for easy comparison of small concentrations, which is especially useful in environmental studies where contaminants are present in very low amounts.

CHEMISTRY, M2 EQ-Bank 10

A student is asked to prepare 500.0 mL of a 0.150 mol L$^{-1}$ standard solution of oxalic acid $\ce{(C2H2O4.2H2O)}$, and then to perform a dilution to produce 250.0 mL of a 0.0300 mol L$^{-1}$ solution. Outline and explain each step in this process, including the calculations involved and choice of equipment. (5 marks)

--- 12 WORK AREA LINES (style=lined) ---

Justify the procedure in part (a.) by explaining two measures taken to ensure the accuracy of the standard solution and diluted solution produced. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. Calculate the mass of oxalic acid:

$MM\ce{(C2H2O4.2H2O)}= 2(12.01) + 2(1.008) + 4(16.00) + 4(1.008) +2(16.00) = 126.068\ \text{g mol}^{-1}$

$n\ce{(C2H2O4.2H2O)} = c \times V = 0.150 \times 0.5 = 0.075\ \text{mol}$

$m\ce{(C2H2O4.2H2O)} = 0.075 \times 126.068 = 9.455\ \text{g}$

Measure 9.455 g of oxalic acid using an electronic balance.

Prepare the standard solution:

Transfer the oxalic acid to a 500.0 mL volumetric flask using a funnel and rinse any remaining crystals from the weighing container into the flask with a small amount of distilled water.
Fill the volumetric flask with distilled water to about 80% full and swirl to dissolve the oxalic acid completely and carefully add more distilled water with a pipette until the bottom of the meniscus rests on the 500.0 mL mark to ensure precise volume.
Stopper the flask and invert several times to ensure a homogeneous solution.

Perform the dilution:

$V_1=\dfrac{c_2V_2}{c_1} = \dfrac{0.03 \times 250}{0.15} = 50\ \text{mL}$

Use a pipette to transfer 50.0 mL of the 0.150 mol L$^{-1}$ solution into a 250.0 mL volumetric flask.
Dilute with distilled water up to the 250.0 mL mark in the flask to achieve a concentration of 0.0300 mol L$^{-1}$.

b. Answers could include two of the following:

A volumetric flask is used for both the standard solution and the diluted solution, as it provides precise measurements for the final solution volume. This accuracy is essential for ensuring the concentration is exactly as calculated.
The primary solute is weighed on an electronic balance to the nearest 0.01 g or better, minimising any error in the amount of solute added to the solution.
The pipette provides precise measurements crucial for accurate dilutions.
Using oxalic acid as the primary standard for the investigation. Primary standard’s have high molar masses and are anhydrous (don’t absorb water). This ensures the substance is pure and the electronic balance can accurately weigh the sample.

Show Worked Solution

a. Calculate the mass of oxalic acid:

$MM\ce{(C2H2O4.2H2O)}= 2(12.01) + 2(1.008) + 4(16.00) + 4(1.008) +2(16.00) = 126.068\ \text{g mol}^{-1}$

$n\ce{(C2H2O4.2H2O)} = c \times V = 0.150 \times 0.5 = 0.075\ \text{mol}$

$m\ce{(C2H2O4.2H2O)} = 0.075 \times 126.068 = 9.455\ \text{g}$

Measure 9.455 g of oxalic acid using an electronic balance.

Prepare the standard solution:

Transfer the oxalic acid to a 500.0 mL volumetric flask using a funnel and rinse any remaining crystals from the weighing container into the flask with a small amount of distilled water.
Fill the volumetric flask with distilled water to about 80% full and swirl to dissolve the oxalic acid completely and carefully add more distilled water with a pipette until the bottom of the meniscus rests on the 500.0 mL mark to ensure precise volume.
Stopper the flask and invert several times to ensure a homogeneous solution.

Perform the dilution:

$V_1=\dfrac{c_2V_2}{c_1} = \dfrac{0.03 \times 250}{0.15} = 50\ \text{mL}$

Use a pipette to transfer 50.0 mL of the 0.150 mol L$^{-1}$ solution into a 250.0 mL volumetric flask.
Dilute with distilled water up to the 250.0 mL mark in the flask to achieve a concentration of 0.0300 mol L$^{-1}$.

b. Answers could include two of the following:

A volumetric flask is used for both the standard solution and the diluted solution, as it provides precise measurements for the final solution volume. This accuracy is essential for ensuring the concentration is exactly as calculated.
The primary solute is weighed on an electronic balance to the nearest 0.01 g or better, minimising any error in the amount of solute added to the solution.
The pipette provides precise measurements crucial for accurate dilutions.
Using oxalic acid as the primary standard for the investigation. Primary standard’s have high molar masses and are anhydrous (don’t absorb water). This ensures the substance is pure and the electronic balance can accurately weigh the sample.

Statistics, EXT1 S1 2024 HSC 7 MC

A driver's knowledge test contains 30 multiple-choice questions, each with 4 options. An applicant must get at least 29 correct to pass.

If an applicant correctly answers the first 25 questions and randomly guesses the last 5 questions, what is the probability that the applicant will pass the test?

$\dfrac{1}{256}$
$\dfrac{15}{1024}$
$\dfrac{1}{64}$
$\dfrac{21}{256}$

Show Answers Only

$C$

Show Worked Solution

$\text{For each of the last 5 questions:}$

$P(C) = \dfrac{1}{4}, \ \ P(\bar{C}) = \dfrac{3}{4}$

$P(\text{at least 4 correct})$	$=\ ^5C_4 \Bigg(\dfrac{1}{4}\Bigg)^{4} \Bigg(\dfrac{3}{4}\Bigg)^{1} + \ ^5C_5 \Bigg(\dfrac{1}{4}\Bigg)^{5}\Bigg(\dfrac{3}{4}\Bigg)^{0}$
	$=5 \times \dfrac{1}{256} \times \dfrac{3}{4}+1\times \dfrac{1}{1024} \times 1$
	$=\dfrac{1}{64}$

$\Rightarrow C$

♦ Mean mark 44%.

Functions, EXT1 F1 2024 HSC 6 MC

How many real value(s) of $x$ satisfy the equation

$\abs{b} = \abs{b\,\sin(4x)}$,

where $x \in [0, 2\pi]$ and $b$ is not zero?

$1$
$2$
$4$
$8$

Show Answers Only

$D$

Show Worked Solution

$\abs{b} = \abs{b\,\sin(4x)}\ \ \Rightarrow\ \ \abs{1} = \abs{\sin(4x)}\ \ (b \neq 0)$

$\sin(4x) = \pm 1$

$x \in [0, 2\pi]\ \ \Rightarrow\ \ 4x \in [0, 8\pi]$

$\therefore 8\ \text{real solutions}$

$\Rightarrow D$

♦ Mean mark 53%.

Statistics, 2ADV S3 2024 HSC 25

A function $f(x)$ is defined as

$f(x)=\left\{\begin{array}{ll} 0, & \text { for}\ \ x \lt 0 \\
1-\dfrac{x}{h}, & \text { for}\ \ 0 \leq x \leq h, \\
0, & \text { for}\ \ x \gt h \end{array}\right.$

where $h$ is a constant.

Find the value of $h$ such that $f(x)$ is a probability density function. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
By first finding a formula for the cumulative distribution function, sketch its graph. (2 marks)

--- 7 WORK AREA LINES (style=lined) ---
Find the value of the median of the probability density function $f(x)$ . Give your answer correct to 3 decimal places. (2 marks)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $h=2$

c. $\text{Median}\ =0.586$

Show Worked Solution

a. $f(x)\ \text{is a PDF if:}$

$\displaystyle \int_{0}^{h} 1-\dfrac{x}{h}\,dx$	$=1$
$\Big[x-\dfrac{x^2}{2h} \Big]_0^{h}$	$=1$
$h-\dfrac{h}{2}$	$=1$
$h$	$=2$

b. $ \displaystyle \int 1-\dfrac{x}{2}\,dx = x-\dfrac{x^2}{4} + c$

$\text{At}\ \ x=0, \ \ F(0)=0,\ \ c=0 $

$f(x)=\left\{\begin{array}{ll} 0, & \text { for}\ \ x \lt 0 \\
x-\dfrac{x^2}{4}, & \text { for}\ \ 0 \leq x \leq 2, \\
1, & \text { for}\ \ x \gt 2 \end{array}\right.$

♦♦ Mean mark (b) 27%.

c. $\text{Let}\ \ m=\ \text{median of}\ f(x) $

$\displaystyle \int_0^{m} 1-\dfrac{x}{2}\,dx$	$=0.5$
$\Big[ x-\dfrac{x^2}{4} \Big]_0^m$	$=0.5$
$m-\dfrac{m^2}{4}$	$=0.5$
$4m-m^2$	$=2$
$m^2-4m+2$	$=0$
$(m-2)^2$	$=2$
$m$	$=2 \pm \sqrt{2}$

$\therefore \ \text{Median}$	$=2-\sqrt{2}\ \ (x \in [0,2]) $
	$=0.586\ \text{(3 d.p.)}$

♦♦ Mean mark (c) 38%.

Measurement, STD1 M5 2024 HSC 32

A scale diagram is shown with locations $A, B$ and $C$ marked (assume grid squares are 1 cm × 1 cm).

Jo takes 24 minutes to walk from $A$ to $B$ (in a straight line) when walking at 3 km per hour.

What is the scale used in the diagram? (3 marks)
--- 7 WORK AREA LINES (style=lined) ---
What is the distance from $B$ to $C$, in kilometres? (2 marks)
--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $1:20\,000$

b. $\text{1.4 km}$

Show Worked Solution

a. $\text{Find distance }A\rightarrow B:$

$D=S \times T = 3 \times \dfrac{24}{60} = 1.2\ \text{km}$

	$\text{Scale }\rightarrow\ 6\ \text{cm }$	$:\ 1.2\ \text{km}$
	$6\ \text{cm }$	$:\ 1200\ \text{m}$
	$6\ \text{cm }$	$:\ 1200\times 100\ \text{cm}$
	$6\ $	$:\ 120\,000$
	$1\ $	$:\ 20\,000$

♦♦♦ Mean mark 15%.

b. $\text{Distance }B\rightarrow C = 7\ \text{grid units}$

$\text{Real distance }B\rightarrow C$	$=7 \times 20\,000$
	$=140\,000\ \text{cm}$
	$=1400\ \text{m}$
	$=1.4\ \text{km}$

♦♦♦ Mean mark 28%.

Algebra, STD1 A3 2024 HSC 23

Carrie is organising a fundraiser.

The cost of hiring the venue and the band is $2500. The cost of providing meals is $50 per person.

Complete the table of values to show the total cost of the fundraiser. (1 mark)

--- 0 WORK AREA LINES (style=lined) ---

\begin{array} {|l|c|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} \text{Number of people} \rule[-1ex]{0pt}{0pt} & \ \ \ \ 0\ \ \ \ & 25 & 50 & 75 & 100 & 125 & 150 \\
\hline
\rule{0pt}{2.5ex} \text{Cost} \rule[-1ex]{0pt}{0pt} & & 3750 & 5000 & 6250 & 7500 & 8750 & 10\,000 \\
\hline
\end{array}

Carrie decides that tickets should be sold at $70 per person. The graph shows the expected revenue at this ticket price. Using the information in part (a), plot the line that shows the cost of the fundraiser. (2 marks)
--- 0 WORK AREA LINES (style=lined) ---

How many tickets need to be sold for the fundraiser to break even? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Carrie sold 300 tickets. How much profit did the fundraiser make? (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $\text{Cost when 0 people }= $2500$

c. $100\ \text{tickets}$

d. $\text{Profit }=$3500$

Show Worked Solution

a. $\text{Cost when 0 people }= $2500$

c. $\text{Point of intersection}\ \ \Rightarrow\ \ \text{break-even}$

$\therefore\ \text{Break-even when 100 tickets sold.}$

Mean mark (c) 53%.

d. $\text{Revenue}\ (R)=70n\ \ (n=\ \text{number of people)}$

$\text{Cost}\ (C)=2500 + \Big(\dfrac{1250}{25}\Big)n=2500+50n$

$\text{Find profit}\ (P)\ \text{when}\ \ n=300:$

$P$	$=R-C$
	$=70\times 300-(2500+50\times300)$
	$=21\,000-17\,500$
	$=$3500$

♦ Mean mark (d) 46%.

Measurement, STD1 M5 2024 HSC 29

A floor plan for a living area is shown. All measurements are in millimetres.

What is the length and width of the cupboard, in metres? (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
The floor of the living area is to be tiled. Tiles will NOT be placed under the cupboard.
Each tile is 0.2 m × 0.5 m. The tiles are supplied in boxes of 15 at a cost of $100 per box. Only full boxes can be purchased.
What is the cost of the tiles for the living area? (4 marks)
--- 12 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $4\ \text{m}\times 0.5\ \text{m}$

b. $$1100$

Show Worked Solution

a. $\text{1 metre = 1000 mm}$

$\text{Cupboard}\ = 4\ \text{m}\times 0.5\ \text{m}$

Mean mark (a) 53%.

b. $\text{Method 1}$

$\text{Total area to be tiled}\ =6\times 3-4\times 0.5=16\ \text{m}^2$

$\text{Area of each tile}\ =0.2\times0.5=0.1\ \text{m}^2$

$\text{Tiles needed}\ =\dfrac{16}{0.1}=160\ \text{tiles}$

$\text{Number of boxes}\ =\dfrac{160}{15}=10.66\dots=11\ \text{boxes}$

$\therefore\ \text{Total cost}\ =100\times 11=$1100$

$\text{Method 2}$

$\text{Tiles to fit 6 m width}\ =\dfrac{6}{0.2}=30 $

$\text{Tiles to fit 2 m width}\ =\dfrac{2}{0.2}=10 $

$\text{Total tiles}\ =30\times 5\ \text{rows}+10\times 1\ \text{rows}\ =160$

$\text{Number of boxes}\ =\dfrac{160}{15}=10.66\dots=11\ \text{boxes}$

$\therefore\ \text{Total cost}\ =100\times 11=$1100$

♦♦ Mean mark (b) 35%.

Financial Maths, STD1 F3 2024 HSC 26

Bobby has a credit card that has no interest-free period.

Interest is charged at 0.07% per day, compounding daily, on the outstanding balance.

How much interest is Bobby charged on an outstanding balance of $600 for 30 days? (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

$$12.73\ \text{(nearest cent)}$

Show Worked Solution

$PV=600,\ \ \ r=\dfrac{0.07}{100},\ \ \ n=30$

$FV$	$=PV(1+r)^n$
	$=600\Big(1+\dfrac{0.07}{100}\Big)^{30}$
	$=612.728\dots$

$\therefore\ \text{Interest}\ =$612.73-$600=$12.73\ \text{(nearest cent)}$

♦♦♦ Mean mark 27%.

Measurement, STD1 M3 2024 HSC 25

In a national park, a straight path connects a lookout to a car park. The lookout is 35 m higher than the car park. The path is inclined at an angle of elevation of 4°, as shown.

What is the length of the path, correct to the nearest metre? (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

$502\ \text{m (nearest metre)}$

Show Worked Solution

$\sin\ 4^\circ$	$=\dfrac{35}{p}$
$p$	$=\dfrac{35}{\sin\ 4^\circ}$
	$=501.74\dots$
	$= 502\ \text{m (nearest metre)}$

♦♦ Mean mark 34%.

Measurement, STD1 M2 2024 HSC 22

The timetable shows an airline schedule in 24-hour time for a flight from Town $A$ to Town $B$.

\begin{array} {|c|c|c|}
\hline
\rule{0pt}{2.5ex} \textit{Flight} \rule[-1ex]{0pt}{0pt} & \textit{Departure} & \textit{Arrival} \\ & \textit{(local time Town A)} & \textit{(local time Town B)} \\
\hline
\rule{0pt}{2.5ex} \text{Town $A$ to Town $B$} \rule[-1ex]{0pt}{0pt} & 1159 & 1336 \\
\hline
\end{array}

When it is 10 am in Town $A$, the time in Town $B$ is 9 am on the same day.

How long does the flight take to travel from Town $A$ to Town $B$? (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

$2\ \text{h}\ 37\ \text{minutes}$

Show Worked Solution

$\text{Town B is 1 hour behind town A.}$

$\Rightarrow \ \text{11:59 in Town A is 10:59 in town B.}$

$\therefore\ \text{Length of flight} =13:36-10:59=2\ \text{h}\ 37\ \text{minutes}$

♦ Mean mark 44%.

Measurement, STD1 M1 2024 HSC 18

A garden is made up of a right-angled triangle and a semicircle as shown.

What is the area of the garden, correct to the nearest square metre? (3 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

$35\ \text{m}^2$

Show Worked Solution

$\text{Base of triangle }=2\times\ \text{radius} = 6\ \text{metres}$

$\text{Total Area }$	$=\text{ Area of triangle + area of semicircle}$
	$=\dfrac{1}{2}\times 6\times 7 + \dfrac{1}{2}\times \pi\times 3^2$
	$=21+14.137\dots$
	$=35.137\dots$
	$=35\ \text{m}^2\ (\text{nearest m}^{2})$

♦♦ Mean mark 33%.

Probability, STD1 S2 2024 HSC 17

A wheel is shown with the numbers 0 to 19 marked.

A game is played where the wheel is spun until it stops.

When the wheel stops, a pointer points to the winning number. Each number is equally likely to win.

List all the even numbers on the wheel that are greater than 7. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
What is the probability that the winning number is NOT an even number greater than 7? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $8\ ,\ 10\ ,\ 12\ ,\ 14\ ,\ 16\ ,\ 18$

b. $0.7$

Show Worked Solution

a. $8\ ,\ 10\ ,\ 12\ ,\ 14\ ,\ 16\ ,\ 18\ \text{(6 numbers)}$

b. $\text{Total numbers = 20}$

$\text{Numbers not even and > 7}\ = 20-6=14\ \text{numbers}$

$P\text{(not even and > 7)}\ =\dfrac{14}{20}=0.7$

♦♦ Mean mark (b) 32%.

Measurement, STD1 M3 2024 HSC 14

A hotel is located 186 m north and 50 m west of a train station.

What is the straight line distance from the hotel to the train station? Round your answer to the nearest metre. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---
What is the bearing of the hotel from the train station? Round your answer to the nearest degree. (2 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $193\ \text{m}$

b. $345^\circ\ \text{(nearest degree)}$

Show Worked Solution

a. $\text{By Pythagoras:}$

	$d^2$	$=50^2+186^2$
	$d^2$	$=37\,096$
	$d$	$=\sqrt{37\,096}$
		$=192.603\dots$
		$=193\ \text{m (nearest metre)}$

♦♦ Mean mark (a) 37%.

b.	$\tan\theta$	$=\dfrac{50}{186}$
	$\theta$	$=15.046\dots^\circ$
		$\approx 15^\circ\ \text{(nearest degree)}$

$\text{Bearing}\ H\ \text{from}\ T =360-15=345^\circ$

♦♦♦ Mean mark (b) 12%.

Statistics, STD1 S1 2024 HSC 13

Consider the following dataset.

$1, \ 1, \ 2, \ 3, \ 5, \ 7, \ 15$

What is the interquartile range? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
By using the outlier formula, determine whether 15 is an outlier. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $\text{IQR = 6}$

b. $15\ \text{is not an outlier as it is not greater than 16.}$

Show Worked Solution

a. $Q_2=3, \ Q_1=1, \ Q_3=7$

$\therefore\ IQR=7-1=6$

♦♦♦ Mean mark (a) 25%.

b. $\text{Find upper fence:}$

$Q_3+1.5\times IQR=7 + 1.5\times 6=16$

$\therefore\ \text{15 is not an outlier (15 < 16)}$

♦♦ Mean mark (b) 32%.

Measurement, STD1 M5 2024 HSC 11

A scale drawing of a tree is shown. The scale is $1 : 50$.

What is the actual height of the tree, in metres? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

$4\ \text{m}$

Show Worked Solution

$8\times 1\ \text{cm}\,$	$:\,8\times 50\ \text{cm}$
$8\ \text{cm}\,$	$:\,400\ \text{cm}$
$8\ \text{cm}\,$	$:\,4\ \text{m}$

$\therefore\ \text{The tree is 4 metres tall.}$

♦ Mean mark 48%.

Algebra, STD1 A3 2024 HSC 10 MC

A cyclist rides a bicycle at a constant speed around a circular track.

Which of the graphs best illustrates the distance of the cyclist from the centre of the track as time varies?

Show Answers Only

$A$

Show Worked Solution

$\text{The bike rider is always a fixed distance from the centre (length of the radius).}$

$\Rightarrow A$

♦ Mean mark 42%.

CHEMISTRY, M2 EQ-Bank 6

Iron $\text{(III)}$ hydroxide can be precipitated from the reaction of iron $\text{(III)}$ nitrate solution with sodium hydroxide solution.

$\ce{Fe(NO3)3(aq) + 3NaOH(aq) -> Fe(OH)3(s) + 3NaNO3(aq)}$

Calculate the mass of precipitate formed when 25.0 mL of 0.150 mol L$^{-1}$ iron $\text{(III)}$ nitrate solution is added to 40.0 mL of 0.250 mol L$^{-1}$ sodium hydroxide solution. (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Calculate the concentration of nitrate ions in the final solution. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $0.356\ \text{g}$

b. $0.173\ \text{mol L}^{-1}$

Show Worked Solution

a. $n\ce{(Fe(NO3)3)} = c \times V = 0.150 \times 0.025 = 0.00375\ \text{mol}$

$n\ce{(NaOH)} = 0.25 \times 0.040 = 0.01\ \text{mol}$

The molar ratio of $\ce{Fe(NO3)3:NaOH} = 1:3$
$3 \times 0.00375 = 0.01125\ \text{mol}$ of $\ce{NaOH}$ is required to react with 0.00375 mol of $\ce{Fe(NO3)3}$.
Due to there only being 0.01 mol of $\ce{NaOH}$ present, $\ce{NaOH}$ will be the limiting reagent.
$n\ce{(Fe(OH)3)}$ formed $=n\ce{(NaOH)} \times \dfrac{1}{3} = 0.01 \times \dfrac{1}{3} = 0.00333\ \text{mol}$
$m\ce{(Fe(OH)3)}= n \times MM = 0.00333 \times (55.85 + 3(1.008) + 3(16.00))= 0.356\ \text{g}$

b. Volume of final solution $=0.025 + 0.040 = 0.065\ \text{L}$

$n\ce{(NO3^-)}= 3 \times n(Fe^{3+}) = 3 \times 0.00375 = 0.01125\ \text{mol}$

$c\ce{(NO3^-)} = \dfrac{n}{V} = \dfrac{0.01125}{0.065} = 0.173\ \text{mol L}^{-1}$

CHEMISTRY, M2 EQ-Bank 4 MC

A 5.0 L sample of water (density = 1.0 kg L$^{-1}$) is contaminated with 15 ppm of mercury ions. What is the mass of mercury in this sample?

75 mg
7.5 mg
15 mg
150 mg

Show Answers Only

$A$

Show Worked Solution

The mass of the water is 5 kg.
15 ppm = 15 mg/kg.
Mass of mercury in the sample $=15 \times 5 = 75\ \text{mg}$.

$\Rightarrow A$

CHEMISTRY, M2 EQ-Bank 5

The compound potassium nitrate has the formula $\ce{KNO3}$

A student makes a solution of this compound by dissolving 40.0 g in 250.0 mL of distilled water. Calculate the concentration of this solution in mol L$^{-1}$. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

The student now requires 500.0 mL of a 5.0% (w/v) solution. What volume of the solution in part (a) is required to make this? (3 marks)

--- 6 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $1.58\ \text{mol L}^{-1}$

b. $0.156\ \text{L}$

Show Worked Solution

a. $n\ce{(KNO3)}= \dfrac{m}{MM} = \dfrac{40.0}{39.10 + 14.01 + 3(16.00)} =0.396\ \text{mol}$

Concentration of solution $=\dfrac{n}{V} = \dfrac{0.396}{0.25} = 1.58\ \text{mol L}^{-1}$

b. A 5% solution requires 5 grams of solute in 100 mL of solution.

Therefore a 500 mL solution requires 25 grams of solute.

$n\ce{(KNO3)} = \dfrac{25}{101.11} = 0.247\ \text{mol}$

$c\ce{(KNO3)} = \dfrac{n}{V} = \dfrac{0.247}{0.5} = 0.494\ \text{mol L}^{-1}$

$c_1V_1$	$=c_2V_2$
$1.58 \times V_1$	$=0.494 \times 0.5$
$V_1$	$=\dfrac{0.247}{1.58}$
$V_1$	$=0.156\ \text{L}$

Measurement, STD1 M4 2024 HSC 31

Wombats can run at a speed of 40 km/h over short distances.

At this speed, how many seconds would it take a wombat to run 150 metres? (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{13.5 seconds}$

Show Worked Solution

$\text{Convert km/h to m/sec:}$

$\text{40 km/h}$	$=40\,000\ \text{m/h}$
	$=\dfrac{40\,000}{60 \times 60}\ \text{m/s}$
	$=11.11\ \text{m/s}$

$\therefore\ \text{Time to run 150m}$	$=\dfrac{150}{11.11…}$
	$=13.5\ \text{seconds}$

♦♦♦ Mean mark 25%.

Financial Maths, STD1 F3 2024 HSC 30

The graph shows the decreasing value of an asset.

For the first 4 years, the value of the asset depreciated by $1500 per year, using a straight-line method of depreciation.

After the end of the 4th year, the method of depreciation changed to the declining-balance method at the rate of 35% per annum.

What is the total depreciation at the end of 10 years? (4 marks)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{Total depreciation}\ =$46\,681.57$

Show Worked Solution

$\text{Depreciation after 4 years}\ = 4 \times 1500 = $6000$

$\text{Value after 4 years}\ = 50\,000-6000=44\,000$

$\text{Declining balance used for the next 6 years:}$

$V_0=$44\,000, r=0.35, n=6$

$S$	$=V_0(1-r)^n$
	$=44\,000(1-0.35)^6$
	$=$3318.43$

$\therefore\ \text{Total depreciation}\ =50\,000-3318.43=$46\,681.57$

♦ Mean mark 40%.

Financial Maths, STD1 F2 2024 HSC 28

Alex and Jun each invest $1800 for 5 years.

Alex's investment earns simple interest at a rate of 7.5% per annum.
Jun's investment earns interest at a rate of 6.0% per annum, compounding quarterly.

By calculating the interest earned over the 5 years, determine who will have the greater amount. (3 marks)

--- 8 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text {Alex’s investment:}$

$\text{Interest}=Prn=1800 \times 0.075 \times 5=\$ 675$

$\text {Jun’s investment:}$

$r=\dfrac{6.0\%}{4}=1.5 \% \text { per quarter}$

$\text {Compounding periods }=5 \times 4=20$

$F V=P V(1+r)^n=1800(1+0.015)^{20}=\$ 2424.34$

$\text{Total interest}=F V-P V=2424.34-1800=\$ 624.34$

$\text {Alex’s interest }>\text { Jun’s interest.}$

$\Rightarrow \text{ Alex will have a greater amount (since original investment the same)}$

Show Worked Solution

$\text {Alex’s investment:}$

$\text{Interest}=Prn=1800 \times 0.075 \times 5=\$ 675$

♦♦ Mean mark 36%.

$\text {Jun’s investment:}$

$r=\dfrac{6.0\%}{4}=1.5 \% \text { per quarter}$

$\text {Compounding periods }=5 \times 4=20$

$F V=P V(1+r)^n=1800(1+0.015)^{20}=\$ 2424.34$

$\text{Total interest}=F V-P V=2424.34-1800=\$ 624.34$

$\text {Alex’s interest }>\text { Jun’s interest.}$

$\Rightarrow \text{ Alex will have a greater amount (since original investment the same)}$

Networks, STD1 N1 2024 HSC 20

The diagram shows a network with weighted edges.

Draw a minimum spanning tree for this network and determine its weight. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Is it possible to find another spanning tree with the same weight? Give a reason for your answer. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

b. $\text{Yes.}$

$\text{→ The edge}\ FC\ \text{on the MST above could be replaced by the edge}\ BC$

$\text{to create a second MST (with equivalent weight = 24)}$

Show Worked Solution

♦ Mean mark 53%.

b. $\text{Yes.}$

$\text{→ The edge}\ FC\ \text{on the MST above could be replaced by the edge}\ BC$

$\text{to create a second MST (with equivalent weight = 24)}$

♦♦♦ Mean mark 16%.

Measurement, STD1 M4 2024 HSC 16

The cost of electricity is 30.13 cents per kWh .

Calculate the cost of using a 650 W air conditioner for 6 hours. (2 marks)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{Cost} =\$ 1.18$

Show Worked Solution

$\text{Usage}=6 \times 650=3900\, \text{W}=3.9\, \text{kW}$

$\text{Cost} =3.9 \times 30.13=117.507 \,\text{c}=\$ 1.18 \, \text {(nearest cent)}$

♦♦ Mean mark 32%.

Financial Maths, STD1 F2 2024 HSC 8 MC

Three years ago, the price of a uniform was $180.

Due to inflation, the price increased annually by 2.5%.

What is the price of this uniform now?

$180.14
$ 181.35
$ 193.50
$ 193.84

Show Answers Only

$D$

Show Worked Solution

$r=2.5 \%=\dfrac{2.5}{100}=0.025$

	$FV$	$=PV(1+r)^n$
		$=180(1.025)^3$
		$=193.84$

$\Rightarrow D$

♦♦ Mean mark 38%.

Measurement, STD1 M3 2024 HSC 7 MC

Consider the diagram shown.

Which of the following is the correct expression for the length of $x$ ?

$20\, \cos 40^{\circ}$
$20\, \sin 40^{\circ}$
$\dfrac{20}{\cos 40^{\circ}}$
$\dfrac{20}{\sin 40^{\circ}}$

Show Answers Only

$A$

Show Worked Solution

$\cos 40^{\circ}$	$=\dfrac{x}{20}$
$x$	$=20\, \times \cos 40^{\circ}$

$\Rightarrow A$

♦ Mean mark 49%.

Networks, STD1 N1 2024 HSC 6 MC

The map shows regions within a country.

A network diagram is to be drawn to represent this map. Vertices will be used to indicate each region and edges will be used to represent a border shared between two regions.

How many edges will there be in the network diagram?

$8$
$7$
$6$
$5$

Show Answers Only

$B$

Show Worked Solution

$\text{Network diagram:}$

$\text{Network has 7 edges.}$

$\Rightarrow B$

♦♦ Mean mark 30%.

Calculus, 2ADV C4 2024 HSC 10 MC

The diagram shows the graph $y = f(x)$.

The point $Q$ is a horizontal point of inflection.

Let $A(x)= \displaystyle \int_0^x f(t)\,dt$.

How many points of inflection does the graph $y=A(x)$ have?

$2$
$3$
$4$
$5$

Show Answers Only

$B$

Show Worked Solution

$A(x) = \displaystyle \int_0^x f(t)\,dt \ \text{(note this definite integral produces a}\ F(x)\text{)}$

$A^{′}(x) = f(x) $

$A^{″}(x) = f^{′}(x) $

♦♦ Mean mark 41%.

$\text{POI requirements:}\ A^{″}(x) = 0\ \text{and sign (concavity) changes either side.}$

$\text{Inspect graph of}\ f(x)\ \text{to find where}\ \ f^{′}(x)=0\ \ \text{and gradient changes}$

$\text{either side of possible points.}$

$\text{→ the three turning points all qualify}$

$\text{→ point}\ Q\ \text{does not qualify (gradient is positive both sides)}$

$\Rightarrow B$

Functions, 2ADV F2 2024 HSC 7 MC

The diagram shows the graph $y = f(x)$.

Which of the following best represents the graph $y = f(2x-1)$?

Show Answers Only

$C$

Show Worked Solution

$\text{At}\ \ x=0:$

$f(2x-1)=f(-1)\ \ \Rightarrow\ \ \text{Eliminate}\ A\ \text{and}\ B.$

$\text{Consider the transformations of}\ f(x) \rightarrow\ f(2x-1) $

$\rightarrow\ \text{Shift}\ f(x)\ \text{1 unit to the right.}$

$\rightarrow\ \text{Dilate}\ f(x-1)\ \text{by a factor of}\ \dfrac{1}{2}\ \text{from the}\ y\text{-axis.}$

$\Rightarrow C$

♦ Mean mark 47%.

Calculus, 2ADV C3 2024 HSC 31

Two circles have the same centre $O$. The smaller circle has radius 1 cm, while the larger circle has radius $(1 + x)$ cm. The circles enclose a region $QRST$, which is subtended by an angle $\theta$ at $O$, as shaded.

The area of $QRST$ is $A$ cm$^{2}$, where $A$ is a constant and $A \gt 0$.

Let $P$ cm be the perimeter of $QRST$.

By finding expressions for the area and perimeter of $QRST$, show that $P(x)=2x+\dfrac{2A}{x}$. (3 marks)
--- 10 WORK AREA LINES (style=lined) ---
Show that if the perimeter, $P(x)$, is minimised, then $\theta$ must be less than 2. (3 marks)
--- 14 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $\text{Area}\ =\ \text{Sector}\ OQR-\text{Sector}\ OTS$

$A$	$=\dfrac{\theta}{2\pi} \times \pi (1+x)^2-\dfrac{\theta}{2\pi} \times \pi \times 1^2$
$A$	$=\dfrac{\theta}{2} (1+x)^2-\dfrac{\theta}{2}$
$A$	$=\dfrac{\theta}{2}(1+2x+x^2-1)$
$A$	$=\dfrac{\theta}{2}x(x+2)$
$\theta$	$=\dfrac{2A}{x(x+2)}$

$\text{Perimeter}\ QRST$	$=\dfrac{\theta}{2\pi} \times 2\pi(x+1)+\dfrac{\theta}{2\pi} \times 2\pi (1)+2x $
	$=\theta(x+1)+\theta+2x$
	$=\theta(x+2)+2x$
	$=\dfrac{2A}{x(x+2)}(x+2)+2x$
	$=2x+\dfrac{2A}{x}$

b. $P(x)=2x+\dfrac{2A}{x}$

$P^{′}(x) = 2-\dfrac{2A}{x^2}$

$P^{″}(x) = \dfrac{4A}{x^3} \gt0\ \ (x,A \gt 0)$

$\Rightarrow\ \text{MIN when}\ \ P^{′}(x)=0:$

$2-\dfrac{2A}{x^2}$	$=0$
$2x^2$	$=2A$
$x^2$	$=A$

$\text{Using part (a):}$

$\theta$	$=\dfrac{2A}{x(x-2)}$
	$=\dfrac{2x^2}{x(x+2)}$
	$=\dfrac{2x}{x+2}$
	$=2 \times \dfrac{x}{x+2} $
	$ \lt 2\ \ \Big(\text{since}\ \ \dfrac{x}{x+2} \lt 1 \ \ \text{for all}\ x \Big) $

$\therefore\ \text{If}\ P(x)\ \text{is minimised,}\ \theta \lt 2. $

Show Worked Solution

a. $\text{Area}\ =\ \text{Sector}\ OQR-\text{Sector}\ OTS$

$A$	$=\dfrac{\theta}{2\pi} \times \pi (1+x)^2-\dfrac{\theta}{2\pi} \times \pi \times 1^2$
$A$	$=\dfrac{\theta}{2} (1+x)^2-\dfrac{\theta}{2}$
$A$	$=\dfrac{\theta}{2}(1+2x+x^2-1)$
$A$	$=\dfrac{\theta}{2}x(x+2)$
$\theta$	$=\dfrac{2A}{x(x+2)}$

$\text{Perimeter}\ QRST$	$=\dfrac{\theta}{2\pi} \times 2\pi(x+1)+\dfrac{\theta}{2\pi} \times 2\pi (1)+2x $
	$=\theta(x+1)+\theta+2x$
	$=\theta(x+2)+2x$
	$=\dfrac{2A}{x(x+2)}(x+2)+2x$
	$=2x+\dfrac{2A}{x}$

♦ Mean mark (a) 41%.
COMMENT: Sector/arc calculations used in solution are for those who don’t want to remember formulas.

b. $P(x)=2x+\dfrac{2A}{x}$

$P^{′}(x) = 2-\dfrac{2A}{x^2}$

$P^{″}(x) = \dfrac{4A}{x^3} \gt0\ \ (x,A \gt 0)$

$\Rightarrow\ \text{MIN when}\ \ P^{′}(x)=0:$

$2-\dfrac{2A}{x^2}$	$=0$
$2x^2$	$=2A$
$x^2$	$=A$

$\text{Using part (a):}$

$\theta$	$=\dfrac{2A}{x(x-2)}$
	$=\dfrac{2x^2}{x(x+2)}$
	$=\dfrac{2x}{x+2}$
	$=2 \times \dfrac{x}{x+2} $
	$ \lt 2\ \ \Big(\text{since}\ \ \dfrac{x}{x+2} \lt 1 \ \ \text{for all}\ x \Big) $

$\therefore\ \text{If}\ P(x)\ \text{is minimised,}\ \theta \lt 2. $

♦♦♦ Mean mark (b) 12%.

Financial Maths, 2ADV M1 2024 HSC 24

Jack intends to deposit $80 into a savings account on the first day of each month for 24 months. The interest rate during this time is 6% per annum, compounded monthly.

Calculate how much money Jack will have in his account at the end of the 24 months. (3 marks)
--- 10 WORK AREA LINES (style=lined) ---
A table of future value interest factors could have been used to calculate how much money Jack would have in his account at the end of the 24 months.
Part of the table is shown.

What is the value of $A$ in the table? Give your answer correct to 3 decimal places. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $A_{24}=\$2044.73$

b. $A=25.559$

Show Worked Solution

a. $r=\dfrac{6\%}{12}=0.5\%\ \text{per month}$

$\text{Let}\ \ A_n=\ \text{Amount after}\ n\ \text{months}$

$A_1$	$=80(1.005)$
$A_2$	$=[80(1.005)+80](1.005)$
	$=80(1.005)^2+80(1.005) $
$\vdots$
$A_n$	$=80(1.005)^n+80(1.005)^{n-1}+ … + 80(1.005) $
	$=80\underbrace{(1.005+1.005^2+ … + 1.005^n)}_{\text{GP where}\ \ a=1.005, r=1.005} $
	$=80\Bigg(\dfrac{1.005(1.005^{n}-1)}{1.005-1}\Bigg) $

$\text{After 24 months:}$

$A_{24}$	$=80\Bigg(\dfrac{1.005(1.005^{24}-1)}{1.005-1}\Bigg) $
	$=$2044.73 \ \text{(nearest cent)}$

♦♦ Mean mark (a) 38%.

b.	$FV$	$= 80 \times A$
	$2044.73$	$=80 \times A$
	$A$	$=\dfrac{2044.73}{80}$
		$=25.5591…$
		$=25.559\ \text{(3 d.p.)}$

Mean mark (b) 51%.

Calculus, 2ADV C4 2024 HSC 22

The graph of the function $f(x) = \ln(1 + x^{2})$ is shown.

Prove that $f(x)$ is concave up for $-1 < x < 1$. (3 marks)
--- 10 WORK AREA LINES (style=lined) ---
A table of function values, correct to 4 decimal places, for some $x$ values is provided.

\begin{array} {|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} x \rule[-1ex]{0pt}{0pt} & 0 & 0.25 & 0.5 & 0.75 & 1 \\
\hline
\rule{0pt}{2.5ex} \ln(1+x^2) \rule[-1ex]{0pt}{0pt} & \ \ \ \ 0\ \ \ \ & 0.0606 & 0.2231 & 0.4463 & 0.6931 \\
\hline
\end{array}

Using the function values provided and the trapezoidal rule, estimate the shaded area in the diagram. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Is the answer to part (b) an overestimate or underestimate? Give a reason for your answer. (1 mark)
--- 5 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $f(x)= \ln(1+x^2)$

$f^{′}(x)=\dfrac{2x}{1+x^2}$

$f^{″}(x)$	$=\dfrac{2(1+x^2)-2x(2x)}{(1+x^2)^2}$
	$=\dfrac{2+2x^2-4x^2}{(1+x^2)^2}$
	$=\dfrac{2(1-x^2)}{(1+x^2)^2}$

$\text{Consider domain}\ x \in(-1,1)\ \ \Rightarrow\ \ 1-x^2>0 $

$(1+x^2)^2 \gt 0\ \ \text{for all}\ x$

$\Rightarrow \ f^{″}(x) \gt 0\ \text{for}\ x \in(-1,1) $

$\therefore f(x)\ \text{is concave up for}\ x \in(-1,1) $

b. $\text{Total shaded area}\ \approx 0.5383\ \text{(4 d.p.)}$

c. $\text{Trapezoidal rule assumes straight lines join points in the table.}$

$\text{Since the graph is concave up in the given domain, the trapezoidal rule will}$

$\text{overestimate the area.}$

Show Worked Solution

a. $f(x)= \ln(1+x^2)$

$f^{′}(x)=\dfrac{2x}{1+x^2}$

$f^{″}(x)$	$=\dfrac{2(1+x^2)-2x(2x)}{(1+x^2)^2}$
	$=\dfrac{2+2x^2-4x^2}{(1+x^2)^2}$
	$=\dfrac{2(1-x^2)}{(1+x^2)^2}$

$\text{In domain}\ x \in(-1,1)\ \ \Rightarrow\ \ 1-x^2>0 $

$(1+x^2)^2 \gt 0\ \ \text{for all}\ x$

$\Rightarrow \ f^{″}(x) \gt 0\ \text{for}\ x \in(-1,1) $

$\therefore f(x)\ \text{is concave up for}\ x \in(-1,1) $

♦ Mean mark (a) 47%.

b. $\text{Total shaded area}$

$\approx 2 \times \dfrac{h}{2}[ y_0 + 2(y_1+y_2+y_3) + y_4] $

$\approx 2 \times \dfrac{0.25}{2}[ 0 + 2(0.0606+0.2231+0.4463) + 0.6931] $

$\approx 0.538275 $

$\approx 0.5383\ \text{(4 d.p.)}$

♦ Mean mark (b) 50%.

c. $\text{Trapezoidal rule assumes straight lines join points in the table.}$

$\text{Since the graph is concave up in the given domain, the trapezoidal rule will}$

$\text{overestimate the area.}$

♦ Mean mark (c) 49%.

Financial Maths, STD2 F5 2024 HSC 20

The table shows the future value for an annuity of $1 for varying interest rates and time periods.

Ken invests $200 at the start of each year for eight years, at an interest rate of 5% per annum.
Calculate the future value of Ken's investment. (1 mark)

--- 2 WORK AREA LINES (style=lined) ---
Shay is planning to take a holiday in three years. She needs $4500 for this holiday and will make regular six-monthly payments into an account that earns interest at the rate of 4% per annum, compounded 6 monthly.
What is the minimum amount Shay needs to pay into this account every 6 months? Give your answer to the nearest $10. Support your answer with calculations. (2 marks)

--- 7 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $F V=\$ 2005.32$

b. $\$700$

Show Worked Solution

a. $\text {8 annual periods at 5% p.a.} \Rightarrow \text { Factor}=10.0266$

$F V=200 \times 10.0266=\$ 2005.32$

b. $r=\dfrac{4 \%}{2}=2 \%\ \text{per 6 months}$

$\text {Compounding periods}=3 \times 2=6$

$\Rightarrow \text {Factor }=6.4343$

$4500$	$=\ \text{Annuity} \times 6.4343$
$\text{Annuity}$	$=\dfrac{4500}{6.4343}$
	$=699.38$
	$=\$700\ \text{(nearest \$10)}$

♦ Mean mark (b) 51%.

Networks, STD2 N2 2024 HSC 18f

The diagram shows a network with weighted edges.

Draw a minimum spanning tree for this network and determine its weight. (2 marks)

--- 0 WORK AREA LINES (style=lined) ---

Is it possible to find another spanning tree with the same weight? Give a reason for your answer. (1 mark)

--- 3 WORK AREA LINES (style=lined) ---

Show Answers Only

b. $\text{Yes.}$

$\text{→ The edge}\ FC\ \text{on the MST above could be replaced by the edge}\ BC\ \text{to create}$

$\text{a second MST (with equivalent weight = 24)}$

Show Worked Solution

b. $\text{Yes.}$

$\text{→ The edge}\ FC\ \text{on the MST above could be replaced by the edge}\ BC\ \text{to create}$

$\text{a second MST (with equivalent weight = 24)}$

♦ Mean mark (b) 45%.

Statistics, STD2 S4 2024 HSC 19

A teacher was exploring the relationship between students' marks for an assignment and their marks for a test. The data for five different students are shown on the graph.

The least-squares regression line is also shown.

What is the equation of the least-squares regression line for this dataset? (2 marks)

--- 4 WORK AREA LINES (style=lined) ---
Another student, whose marks are not on the graph, scored 5 for the assignment and 12 on the test.
Did this student do better or worse on the test than the regression line predicts? Provide a reason for your answer. (1 mark)

--- 4 WORK AREA LINES (style=lined) ---

Show Answers Only

a. $\text {Data points: }(3,11),(5,14),(6,12),(7,15),(9,20)$

$y \,\text {-intercept}=6$

$m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{20-6}{10-0}=1.4$

$\text{LSRL}\ \ \Rightarrow \ y=1.4x+6$

b. $\text {The student’s mark \((5,12)$ sits below the LSRL.}\)

$\text {Therefore the student did worse than expected.}$

Show Worked Solution

a. $\text {Data points: }(3,11),(5,14),(6,12),(7,15),(9,20)$

$y\,\text {-intercept}=6$

$m=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{20-6}{10-0}=1.4$

$\text{LSRL}\ \ \Rightarrow \ y=1.4x+6$

♦ Mean mark (a) 46%.

b. $\text {The student’s mark \((5,12)$ sits below the LSRL.}\)

$\text {Therefore the student did worse than expected.}$

Financial Maths, 2ADV M1 2024 HSC 26

Twenty-five years ago, Phoenix deposited a single sum of money into a new bank account, earning 2.4% interest per annum compounding monthly.

Present value interest factors for an annuity of $1 for various interest rates $(r)$ and numbers of periods $(n)$ are given in the table.

Phoenix made the following withdrawals from this account.

$2000 at the end of each month for the first 15 years, starting at the end of the first month.
$1200 at the end of each month for the next 10 years, starting at the end of the 181st month after the account was opened.

Calculate the minimum sum that Phoenix could have deposited in order to make these withdrawals. (4 marks)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{Minimum deposit}\ = $391\,344.80$

Show Worked Solution

$\text{1st Annuity}$

$\text{Find PVA for \$2000 paid monthly for 1st 15 years:}$

$r= \dfrac{2.4%}{12} = 0.2\% = 0.002$

$\text{Total payments (to Phoenix)}\ = 15 \times 12 = 180$

$\text{PVA factor (from table)}\ = 151.036$

$\text{PVA (1st annuity)}\ = 2000 \times 151.036 = $302\,072$

♦ Mean mark 51%.

$\text{2nd Annuity}$

$\text{Find PVA for \$1200 paid monthly from year 16 to 25:}$

$\text{PVA (2nd annuity) = PVA (25 years) }-\text{ PVA (15 years)}$

$r= \dfrac{2.4%}{12} = 0.2\% = 0.002$

$\text{Total payments (25 years)}\ = 25 \times 12 = 300$

$\text{PVA factors (from table): 225.430 (25 years), 151.036 (15 years)}$

$\text{PVA (2nd annuity)}$	$=(1200 \times 225.430)-(1200 \times 151.036)$
	$=$89\,272.80$

$\therefore\ \text{Minimum deposit}\ = 302\,072+89\,272.80 = $391\,344.80$

Financial Maths, STD2 F5 2024 HSC 41

Twenty-five years ago, Phoenix deposited a single sum of money into a new bank account, earning 2.4% interest per annum compounding monthly.

Present value interest factors for an annuity of $1 for various interest rates $(r)$ and numbers of periods $(n)$ are given in the table.

Phoenix made the following withdrawals from this account.

$2000 at the end of each month for the first 15 years, starting at the end of the first month.
$1200 at the end of each month for the next 10 years, starting at the end of the 181st month after the account was opened.

Calculate the minimum sum that Phoenix could have deposited in order to make these withdrawals. (4 marks)

--- 10 WORK AREA LINES (style=lined) ---

Show Answers Only

$\text{Minimum deposit}\ = $391\,344.80$

Show Worked Solution

$\text{1st Annuity}$

$\text{Find PVA for \$2000 paid monthly for 1st 15 years:}$

$r= \dfrac{2.4%}{12} = 0.2\% = 0.002$

$\text{Total payments (to Phoenix)}\ = 15 \times 12 = 180$

$\text{PVA factor (from table)}\ = 151.036$

$\text{PVA (1st annuity)}\ = 2000 \times 151.036 = $302\,072$

♦♦ Mean mark 39%.

$\text{2nd Annuity}$

$\text{Find PVA for \$1200 paid monthly from year 16 to 25:}$

$\text{PVA (2nd annuity) = PVA (25 years) }-\text{ PVA (15 years)}$

$r= \dfrac{2.4%}{12} = 0.2\% = 0.002$

$\text{Total payments (25 years)}\ = 25 \times 12 = 300$

$\text{PVA factors (from table): 225.430 (25 years), 151.036 (15 years)}$

$\text{PVA (2nd annuity)}$	$=(1200 \times 225.430)-(1200 \times 151.036)$
	$=$89\,272.80$

$\therefore\ \text{Minimum deposit}\ = 302\,072+89\,272.80 = $391\,344.80$

\(b\)	\(=r \times \dfrac{s_y}{s_x}\)
\(-1.27\)	\(=r\times\dfrac{19}{8.51}\)
\(\therefore\ r\)	\(=\dfrac{-1.27\times 8.51}{19}\)
	\(=-0.5688\dots\)

\(males\)	\(=67.5-1.27\times number\)
\(25.6\)	\(=67.5-1.27\times number\)
\(number\)	\(=\dfrac{67.5-25.6}{1.27}\)
	\(=32.992\dots\)
	\(\approx 33\)

\(\text{Upper boundary}\)	\(=Q_3+1.5\times IQR\)
	\(=48+1.5\times 43\)
	\(=112.5\)

	\((\gamma+\bar{\gamma})^3-3(\gamma+\bar{\gamma})+1\)
		\(=\gamma^3+3 \gamma^2 \bar{\gamma}+3 \gamma \bar{\gamma}^2+\bar{\gamma}^3-3 \gamma-3 \bar{\gamma}+1\)
		\(=\gamma^3+3 \gamma\abs{\gamma}^2+3 \bar{\gamma}\abs{\gamma}^2+\bar{\gamma}^3-3 \gamma-3 \bar{\gamma}+1\)
		\(=w+3 \gamma+3 \bar{\gamma}+\bar{w}-3 \gamma-3 \bar{\gamma}+1\)
		\(=w+\bar{w}+1\)
		\(=0 \quad \text{(Sum of complex roots of 1 = 0)}\)

	\((\gamma+\bar{\gamma})_1\)	\(=2 \cos \left(\dfrac{2 \pi}{9}\right)\)
	\((\gamma+\bar{\gamma})_2\)	\(=2 \cos \left(\dfrac{8 \pi}{9}\right)\)
	\((\gamma+\bar{\gamma})_3\)	\(=2 \cos \left(\dfrac{4\pi}{9}\right)\)

	\(\overrightarrow{O R}\)	\(=\overrightarrow{O P}+k \overrightarrow{P Q}\)
		\(=\overrightarrow{O P}+k(\overrightarrow{O Q}-\overrightarrow{O P})\)
		\(=(1-k) \overrightarrow{O P}+k \overrightarrow{O Q}\)
		\(=\dfrac{3}{5}(1-k)\underset{\sim}{a}+3 k \underset{\sim}{b}\)

	\(\dfrac{3}{5}(1-k)\)	\(=1-3 k\)
	\(3-3 k\)	\(=5-15 k\)
	\(k\)	\(=\dfrac{1}{6}\)

	\(\overrightarrow{O R}\)	\(=\overrightarrow{O P}+k \overrightarrow{P Q}\)
		\(=\overrightarrow{O P}+k(\overrightarrow{O Q}-\overrightarrow{O P})\)
		\(=(1-k) \overrightarrow{O P}+k \overrightarrow{O Q}\)
		\(=\dfrac{3}{5}(1-k)\underset{\sim}{a}+3 k \underset{\sim}{b}\)

	\(\dfrac{3}{5}(1-k)\)	\(=1-3 k\)
	\(3-3 k\)	\(=5-15 k\)
	\(k\)	\(=\dfrac{1}{6}\)