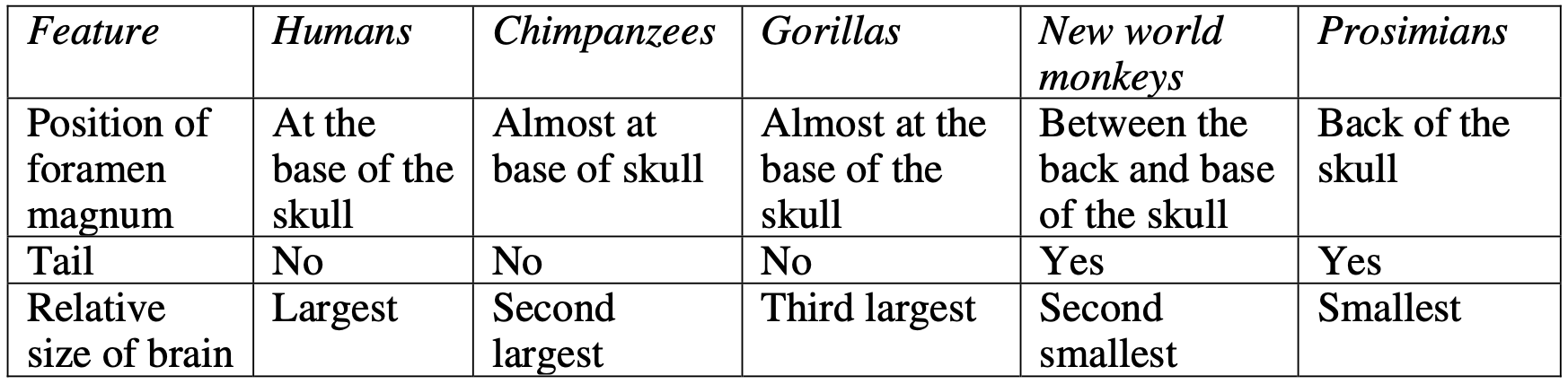
Construct a flow chart to summarise the main steps and products of the light-independent reactions of photosynthesis. (5 marks)
BIOLOGY, M1 2018 HSC 27
With the breakdown of proteins, animals produce ammonia, a nitrogenous waste product that must be removed. Direct removal of ammonia requires the excretion of large amounts of water.
Explain how both terrestrial mammals and insects conserve water while excreting nitrogenous wastes. (4 marks)
--- 6 WORK AREA LINES (style=lined) ---
BIOLOGY, M1 2018 HSC 23
\begin{array} {|l|l|} --- 4 WORK AREA LINES (style=lined) ---
\hline
\rule{0pt}{2.5ex}\textit{Dependent variable}\rule[-1ex]{0pt}{0pt} & \text{•} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\
\hline
\rule{0pt}{2.5ex}\textit{Control}\rule[-1ex]{0pt}{0pt} & \text{•} \\
\hline
\rule{0pt}{2.5ex}\textit{Variables to be kept constant}\rule[-1ex]{0pt}{0pt} & \text{•} \\ & \text{•} \\
\hline
\end{array}
CHEMISTRY, M3 2012 HSC 13-14 MC
Use the information provided to answer Questions 13 and 14.
\begin{array} {|l|}
\hline \text{This equation represents a common redox reaction.} \\ \ \ \ \ce{Cr2O7^{2-}(aq) + 14H+(aq) + 6Fe^{2+}(aq) \rightarrow 2Cr^{3+}(aq) + 6Fe^{3+}(aq) + 7H2O(l)} \\
\hline \end{array}
Question 13
What is the oxidising agent in the reaction?
- \(\ce{H^+}\)
- \(\ce{Cr^3+}\)
- \(\ce{Fe^2+}\)
- \(\ce{Cr2O7^2-}\)
Question 14
What is the value of \(\ce{E}_{\text {cell }}^{\ominus}\) for the reaction?
- 0.59 V
- 0.92 V
- 1.90 V
- 2.13 V
CHEMISTRY, M3 2016 HSC 16 MC
An electrochemical cell has the following structure.
This particular cell can be represented as:
\( \ce{Q} | \ce{Q^2+} || \ce{R^2+} | \ce{R} \)
Which of the following cells would produce the highest cell potential at standard conditions?
- \( \ce{Mg} | \ce{Mg^2+} || \ce{Fe^2+} | \ce{Fe} \)
- \( \ce{Al} | \ce{Al^3+} || \ce{Cu^2+} | \ce{Cu} \)
- \( \ce{Zn} | \ce{Zn^2+} || \ce{Pb^2+} | \ce{Pb} \)
- \( \ce{Ni} | \ce{Ni^2+} || \ce{Ag^+} | \ce{Ag} \)
CHEMISTRY, M3 2017 HSC 11 MC
Consider the following redox reaction.
\( \ce{2K2Cr2O7}(aq) + \ce{2H2O}(l) + \ce{3S}(s) \rightarrow \ce{2Cr2O3}(aq) + \ce{4KOH}(aq) + \ce{3SO2}(g) \)
Which species is being oxidised?
- \( \ce{Cr^6+}\)
- \( \ce{K^+} \)
- \( \ce{O^2-} \)
- \( \ce{S} \)
HMS, HAG 2020 HSC 22
Complete the table for THREE current leading causes of mortality for males and females in Australia. (4 marks)
--- 0 WORK AREA LINES (style=blank) ---
\begin{array}{|c|c|c|}
\hline
\rule{0pt}{2.5ex}\textit{Current leading} & \textit{Trend in mortality rate for} & \textit{Trend in mortality rate for}\\
\rule[-1ex]{0pt}{0pt}\quad \textit{cause of mortality} \quad & \textit{males over the last 10 years} & \textit{females over the last 10 years}\\
\hline
\quad & \quad &\quad\\
\quad & \quad &\quad\\
\quad & \quad &\quad\\
\quad & \quad &\quad\\
\hline
\quad & \quad &\quad\\
\quad & \quad &\quad\\
\quad & \quad &\quad\\
\quad & \quad &\quad\\
\hline
\quad & \quad &\quad\\
\quad & \quad &\quad\\
\quad & \quad &\quad\\
\quad & \quad &\quad\\
\hline
\end{array}
CHEMISTRY, M2 2006 HSC 10 MC
Phosphorus pentoxide reacts with water to form phosphoric acid according to the following equation.
\(\ce{P2O5}(s) + \ce{3H2O}(l) \rightarrow \ce{2H3PO4}(aq)\)
Phosphoric acid reacts with sodium hydroxide according to the following equation.
\(\ce{H3PO4}(aq) + \ce{3NaOH}(aq) \rightarrow \ce{Na3PO4}(aq) + \ce{3H2O}(l)\)
A student reacted 1.42 g of phosphorus pentoxide with excess water.
What volume of 0.30 mol L\(^{-1}\) sodium hydroxide would be required to neutralise all the phosphoric acid produced?
- 0.067 L
- 0.10 L
- 0.20 L
- 5.0 L
CHEMISTRY, M6 2012 HSC 30
A chemist analysed aspirin tablets for quality control. The initial step of the analysis was the standardisation of a \(\ce{NaOH}\) solution. Three 25.00 mL samples of a 0.1034 mol L\(^{-1}\) solution of standardised \(\ce{HCl}\) were titrated with the \( \ce{NaOH} \) solution. The average volume required for neutralisation was 25.75 mL.
- Calculate the molarity of the \(\ce{NaOH}\) solution. (2 marks)
Three flasks were prepared each containing a mixture of 25 mL of water and 10 mL of ethanol. An aspirin tablet was dissolved in each flask. The aspirin in each solution was titrated with the standardised \(\ce{NaOH}\) solution according to the following equation:
\(\ce{C9H8O4(aq) + NaOH(aq) \rightarrow C9H7O4Na(aq) + H2O(l)}\)
The following titration results were obtained.
\begin{array} {|c|c|}
\hline
\rule{0pt}{2.5ex}\textit{Tablet}\rule[-1ex]{0pt}{0pt} & \textit{Volume}\ \text{(mL)}\\
\hline
\rule{0pt}{2.5ex}\text{1}\rule[-1ex]{0pt}{0pt} & 16.60\\
\hline
\rule{0pt}{2.5ex}\text{2}\rule[-1ex]{0pt}{0pt} & 16.50\\
\hline
\rule{0pt}{2.5ex}\text{3}\rule[-1ex]{0pt}{0pt} & 16.55\\
\hline
\end{array}
- Calculate the average mass (mg) of aspirin per tablet. (3 marks)
CHEMISTRY, M2 2013 HSC 28
A student attempted to determine the concentration of a hydrochloric acid solution. The following steps were performed.
Step 1. A conical flask was rinsed with water.
Step 2. A 25.0 mL pipette was rinsed with water.
Step 3. The student filled the pipette with a standard sodium carbonate solution to the level shown in the diagram.

Step 4. The standard sodium carbonate solution in the pipette was transferred to the conical flask. The student ensured that all of the sodium carbonate solution was transferred to the conical flask by blowing through the pipette. Three drops of an appropriate indicator were added to the conical flask.
Step 5. A burette was rinsed with the hydrochloric acid solution and then filled with the acid. The student then carried out a titration to determine the concentration of the hydrochloric acid solution.
In steps 2,3 and 4 above the student did not follow acceptable procedures.
- Identify the mistake the student made in step 4 and propose a change that would improve the validity of the result. (2 marks)
- Explain the effect of the mistakes made in steps 2 and 3 on the calculation of the concentration of the hydrochloric acid solution. (3 marks)
CHEMISTRY, M2 2009 HSC 15 MC
CHEMISTRY, M2 2009 HSC 22
The nitrogen content of bread was determined using the following procedure:
-
- A sample of bread weighing 2.80 g was analysed.
- The nitrogen in the sample was converted into ammonia.
- The ammonia was collected in 50.0 mL of 0.125 mol L\(^{-1}\) hydrochloric acid. All of the ammonia was neutralised, leaving an excess of hydrochloric acid.
- The excess hydrochloric acid was titrated with 23.30 mL of 0.116 mol L\(^{-1}\) sodium hydroxide solution.
- Write balanced equations for the TWO reactions involving hydrochloric acid. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Calculate the moles of excess hydrochloric acid. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Calculate the moles of ammonia. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Calculate the percentage by mass of nitrogen in the bread. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
CHEMISTRY, M2 2010 HSC 19 MC
Sodium azide is used in automobile airbags to provide a source of nitrogen gas for rapid inflation in an accident.The equation shows the production of nitrogen gas from sodium azide.
\( \ce{2NaN3}(s) \rightarrow \ce{2Na}(s) + \ce{3N2}(g)\)
What mass of sodium azide will produce 40L of \(\ce{N2}\) at 100 kPa and 0°C?
- 70 g
- 76 g
- 114 g
- 172 g
CHEMISTRY, M2 2011 HSC 19 MC
All of the carbon dioxide in a soft drink with an initial mass of 381.04 g was carefully extracted and collected as a gas. The final mass of the drink was 380.41 g.
What volume would the carbon dioxide occupy at 100 kPa and 25°C?
- 0.33 L
- 0.35 L
- 0.56 L
- 0.63 L
CHEMISTRY, M2 2011 HSC 20 MC
When charcoal reacts in the presence of oxygen, carbon monoxide and carbon dioxide are produced according to the following chemical reactions.
\( \ce{C}(s) +\frac{1}{2} \ce{O}_2(g) \rightarrow \mathrm{CO}(g)\)
\(\ce{C}(s) +\ce{O2}(g) \rightarrow \ce{CO2}(g)\)
What would be the total mass of gas produced when 400 g of charcoal is reacted, assuming equal amounts are consumed in each reaction?
- 0.93 kg
- 1.2 kg
- 1.5 kg
- 2.5 kg
CHEMISTRY, M6 2014 HSC 30
CHEMISTRY, M6 2016 HSC 29
A solution of hydrochloric acid was standardised by titration against a sodium carbonate solution using the following procedure.
- All glassware was rinsed correctly to remove possible contaminants.
- Hydrochloric acid was placed in the burette.
- 25.0 mL of sodium carbonate solution was pipetted into the conical flask.
The titration was performed and the hydrochloric acid was found to be 0.200 mol L\(^{-1} \).
- Identify the substance used to rinse the conical flask and justify your answer. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Seashells contain a mixture of carbonate compounds. The standardised hydrochloric acid was used to determine the percentage by mass of carbonate in a seashell using the following procedure.
-
- A 0.145 g sample of the seashell was placed in a conical flask.
- 50.0 mL of the standardised hydrochloric acid was added to the conical flask.
- At the completion of the reaction, the mixture in the conical flask was titrated with 0.250 mol L\(^{-1} \) sodium hydroxide.
- The volume of sodium hydroxide used in the titration was 29.5 mL.
- Calculate the percentage by mass of carbonate in the sample of the seashell. (4 marks)
--- 14 WORK AREA LINES (style=lined) ---
CHEMISTRY, M1 2009 HSC 30c
CHEMISTRY, M1 2010 HSC 35d
Experimental evidence from emission line spectra of gaseous atoms has highlighted both the merits and the limitations of Bohr's atomic model.
Discuss Bohr's atomic model with reference to this evidence. (5 marks)
CHEMISTRY, M1 2011 HSC 7 MC
Which of the following lists contains ONLY unstable isotopes?
- \( \ce{^{207}_{82}Pb}, \ \ce{^{99}_{43}Tc}, \ \ce{^{12}_{7}N} \)
- \( \ce{^{214}_{82}Pb}, \ \ce{^{46}_{20}Ca}, \ \ce{^{99}_{43}Tc}\)
- \( \ce{^{238}_{92}U}, \ \ce {^{40}_{20}Ca}, \ \ce{^{12}_{7}N}\)
- \( \ce{^{238}_{92}U}, \ \ce{^{40}_{20}Ca}, \ \ce{^{99}_{43}Tc}\)
CHEMISTRY, M1 2012 HSC 37e
Evaluate the contribution of the Bohr model to the development of our understanding of the structure of the atom. (7 marks)
BIOLOGY, M4 2015 HSC 35e
'Science has been used to solve problems in the investigation of evolutionary
relationships between humans and other primates, and so has provided information of interest to society.'
Justify this statement in terms of the scientific knowledge behind DNA-DNA hybridisation AND karyotype analysis. (7 marks)
--- 20 WORK AREA LINES (style=lined) ---
BIOLOGY, M4 2015 HSC 35d
- Distinguish between relative dating and absolute dating of fossils. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Students found three fossils (A, B and C) at an archaeological site.
The students concluded that their data were conflicting and they could not determine the relative ages of the fossils.
Evaluate the students' conclusion with reference to the data presented. (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
BIOLOGY, M4 2016 HSC 35d
A new fossil form was recently found in South Africa. This fossil shares characteristics with both the genus Australopithecus and the genus Homo. There has been debate as to whether this new fossil form should be classified in the genus Australopithecus or in the genus Homo. --- 3 WORK AREA LINES (style=lined) --- --- 8 WORK AREA LINES (style=lined) ---
BIOLOGY, M4 2016 HSC 35b
BIOLOGY, M3 2002 HSC 25
- Define the concept of punctuated equilibrium in evolution. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- How does punctuated equilibrium differ from the process proposed by Darwin? (3 marks)
--- 7 WORK AREA LINES (style=lined) ---
BIOLOGY, M3 2009 HSC 27
Most offspring resemble their parents in a number of characteristics, but there are often some characteristics in the offspring that are unexpected.
Explain, using examples, how genetics and the environment can affect the phenotype of individuals. (8 marks)
--- 16 WORK AREA LINES (style=lined) ---
BIOLOGY, M3 2010 HSC 30
BIOLOGY, M3 2014 HSC 26
Explain how Darwin/Wallace's theory of evolution by natural selection and isolation accounts for convergent evolution. Use an example to support your answer. (5 marks)
BIOLOGY, M2 2014 HSC 24
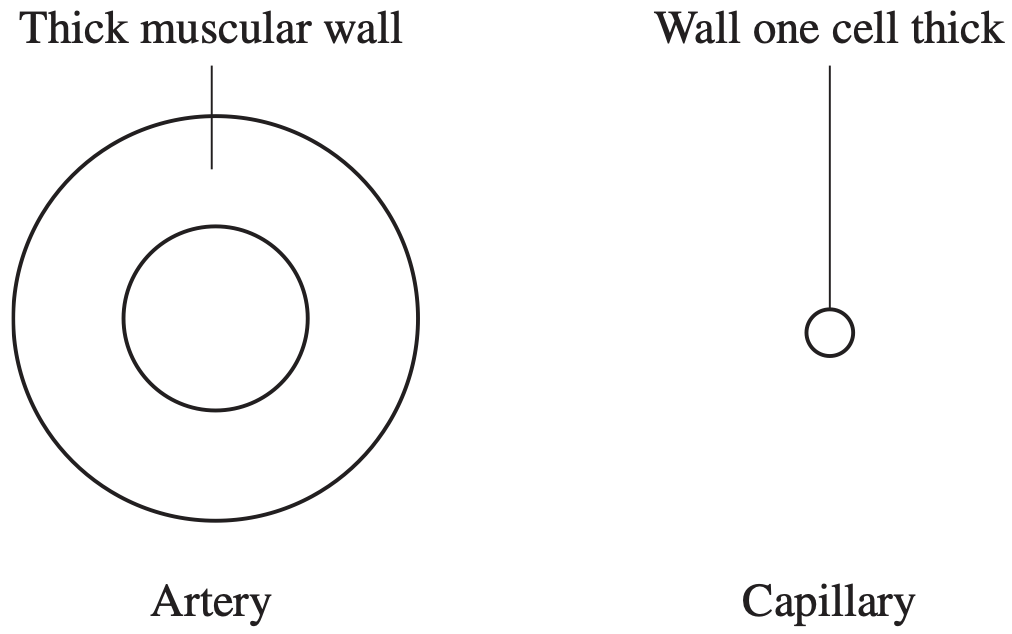
- Use labelled diagrams to distinguish between the structure of an artery and that of a capillary. (2 marks)
--- 8 WORK AREA LINES (style=blank) ---
- Relate one structure of a capillary to its function. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
BIOLOGY, M2 2015 HSC 27
- Outline TWO differences between whole blood and plasma. (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
The steps below show the preparation and use of blood products in the treatment of Ebola Virus Disease. This disease is characterised by significant blood loss.
- Explain why this protocol produces an effective treatment for Ebola Virus Disease. (3 marks)
--- 8 WORK AREA LINES (style=lined) ---
BIOLOGY, M2 2016 HSC 31
As altitude increases, the partial pressure of oxygen \( \text{(p} \ce{O_2)}\) in air decreases.
Species A and B are closely related endotherms that live in different habitats in Asia. The minimum \( \text{p} \ce{O_2}\) required for 100% blood oxygen saturation differs in these species because of differences in their haemoglobin structure. Data related to these two species are shown below.
\begin{equation}
\begin{array}{|c|c|c|}
\hline \text { Endotherm species } & \text { Habitat altitude } & \text { Minimum } \mathrm{pO}_2 \text { for } 100 \%\ \mathrm{Hb} \text { saturation } \\
\hline \mathrm{A} & \mathrm{High} & 54 \\
\mathrm{~B} & \text { Low } & 80 \\
\hline
\end{array}
\end{equation}
Explain how the differences in these species could have arisen, using the Darwin/Wallace theory of evolution and your understanding of the adaptive advantage of haemoglobin. (8 marks)
--- 18 WORK AREA LINES (style=lined) ---
BIOLOGY, M2 2017 HSC 27
- Draw labelled diagrams to distinguish between transverse sections of a xylem vessel and a phloem vessel. (2 marks)
--- 6 WORK AREA LINES (style=blank) ---
- Describe the process that transports sugars through a plant. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
BIOLOGY, M1 2014 HSC 28
Rennin is an enzyme found in the stomach of young mammals. Rennin curdles the milk drunk by the mammal and allows the milk solids to stay longer in the stomach to be further digested. Students conducted an investigation into rennin activity. They bubbled different volumes of carbon dioxide gas into milk samples. Each sample was 50mL and was kept at a constant temperature. The students then added rennin to each milk sample and recorded the time taken for the milk to curdle. --- 4 WORK AREA LINES (style=lined) --- --- 8 WORK AREA LINES (style=lined) ---
BIOLOGY, M1 2013 HSC 25
The graph below shows the results obtained from testing the activity of a bacterial enzyme.
- Name ONE variable, other than temperature, that would have been controlled in the experiment. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- For what temperature range does the enzyme display the maximum rate of change in activity? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Account for the activity of the enzyme at the parts of the graph labelled A, B, C and D. (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
- Based on the information in the graph, suggest the type of environment in which these bacteria might survive. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
BIOLOGY, M1 2015 HSC 22
Explain why insects excrete uric acid as their principal nitrogenous waste. (2 marks)
BIOLOGY, M1 2016 HSC 23
--- 5 WORK AREA LINES (style=lined) --- --- 0 WORK AREA LINES (style=lined) ---
BIOLOGY, M7 SM-Bank 27
Influenza is an infectious respiratory disease. In humans, it can be caused by the influenza A or influenza B viruses. Antigenic drift can result in small changes to the structure of the antigens on the surface of the influenza virus, as shown in the diagram below. --- 1 WORK AREA LINES (style=lined) --- --- 5 WORK AREA LINES (style=lined) ---
BIOLOGY, M6 SM-Bank 25
Over time, the South African cheetah population has suffered drastic reduction due to periodic droughts, disease and hunting. Currently, only small, isolated populations of cheetahs exist in the wild.
Explain, in terms of genetic diversity, why cheetah populations are now on the verge of extinction. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
CHEMISTRY, M5 EQ-Bank 29
The information in the table shows how the solubility of lead chloride is affected by temperature.
Using a graph, calculate the solubility product \((K_{sp})\) of the dissolution of lead chloride at 50°C. Include a fully labelled graph and a relevant chemical equation in your answer (6 marks)
--- 12 WORK AREA LINES (style=lined) ---
CHEMISTRY, M5 EQ-Bank 28
A 100 mL saturated solution of calcium hydroxide at 25°C contains 0.173 g of calcium hydroxide.
- Calculate the solubility product \(\ce{($K_{sp}$)}\) of this salt at 25°C. (3 marks)
--- 7 WORK AREA LINES (style=lined) ---
- Explain why the undissolved solid is not included in the expression for the solubility product constant. (1 marks)
--- 2 WORK AREA LINES (style=lined) ---
CHEMISTRY, M6 EQ-Bank 14 MC
Equal volumes of four different acids are titrated with the same base at 25°.
Information about these acids is given in the table.
Which acid requires the greatest volume of base for complete reaction?
- \(\ce{HCl}\)
- \(\ce{H3PO4}\)
- \(\ce{CH3COOH}\)
- \(\ce{HCN}\)
CHEMISTRY, M6 EQ-Bank 28
The flowchart shown outlines the sequence of steps used to determine the concentration of an unknown hydrochloric acid solution.
Describe steps A, B and C including correct techniques, equipment and appropriate calculations. Determine the concentration of the hydrochloric acid. (8 marks)
--- 16 WORK AREA LINES (style=lined) ---
CHEMISTRY, M6 EQ-Bank 29
Explain why a mixture of acetic acid (1 M) and sodium acetate (1 M) can act as a buffer while a mixture of hydrochloric acid (1 M) and sodium chloride (1 M) cannot. (3 marks)
--- 8 WORK AREA LINES (style=lined) ---
CHEMISTRY, M6 EQ-Bank 24
The pH of a 0.30 M aqueous propanoic acid solution was measured to be 2.7. The dissociation of propanoic acid is represented below.
\(\ce{CH3CH2COOH($aq$) + H2O($l$) \rightleftharpoons CH3CH2COO^-($aq$) + H3O^{+}($aq$)}\)
Calculate the `K_a` of the solution. (3 marks)
CHEMISTRY, M7 EQ-Bank 27
Contrast ONE addition polymer and ONE condensation polymer in terms of their structures, properties and uses. Include structural formulae in your answers. (7 marks)
--- 20 WORK AREA LINES (style=lined) ---
CHEMISTRY, M6 EQ-Bank 25
The graph shows changes in pH for the titrations of equal volumes of solutions of two monoprotic acids, Acid 1 and Acid 2.
Explain the differences between Acid 1 and Acid 2 in terms of their relative strengths and concentrations. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
CHEMISTRY, M5 EQ-Bank 15 MC
What will happen when sulfuric acid is added to a saturated solution of sparingly soluble calcium sulfate?
- The concentration of calcium and sulfate ions will increase over time due to the presence of \(\ce{H^{+}}\) ions.
- The concentration of calcium and sulfate ions will decrease over time due to the presence of \(\ce{H^{+}}\) ions.
- The concentration of calcium and sulfate ions will increase over time due to the presence of \(\ce{SO4^{2-}}\) ions.
- The concentration of calcium and sulfate ions will decrease over time due to the presence of \(\ce{SO4^{2-}}\) ions.
CHEMISTRY, M5 EQ-Bank 13 MC
0.20 moles of phosphorus pentachloride were heated to 200°C in a 2 L container in the presence of a vanadium catalyst according to the following reaction.
\( \ce{PCl5(g) \rightleftharpoons PCl3(g) + Cl2(g)}\)
At equilibrium, the mixture was found to contain 0.16 moles of chlorine.
Which of the following is the equilibrium constant for this reaction at this temperature?
- 0.32
- 0.64
- 1.56
- 3.13
Algebra, STD1 A3 2019 HSC 9 MC
The container shown is initially full of water.
Water leaks out of the bottom of the container at a constant rate.
Which graph best shows the depth of water in the container as time varies?
| A. | B. | ||
| C. | D. |
Financial Maths, STD1 F3 2021 HSC 30
Blake opens a new credit card account on 1 May. He uses it, for the first time, on 4 May to buy concert tickets for $850.
He makes no further purchases or repayments during the month of May.
A statement for the credit card is issued on the last day of each month.
The statement for May shows that interest is charged at 19.75% per annum, compounding daily, from 20 May (included) until 31 May (included).
- What is the compound interest shown on the statement issued on 31 May? (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
- The minimum payment is calculated as 3% of the closing balance on 31 May. Calculate the minimum payment. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
CHEMISTRY, M5 EQ-Bank 21
Three gases \(\ce{X, Y}\) and \(\ce{Z}\) were mixed in a closed container and allowed to reach equilibrium. A change was imposed at time \(\ce{$T$}\) and the equilibrium was re-established. The concentration of each gas is plotted against time.
- What is a possible change that was imposed at time \(\ce{$T$}\)? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Write a chemical reaction that is represented by the concentration graph above. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
CHEMISTRY, M5 EQ-Bank 12 MC
Nitrogen dioxide (a brown gas) and dinitrogen tetroxide (a colourless gas) are both forms of oxides of nitrogen. They are in equilibrium according to the equation
\( \ce{2NO2(g) \rightleftharpoons N2O4(g)}\).
An equilibrium mixture of the two gases at room temperature is light brown but at higher temperatures the colour becomes a much deeper brown.
What conclusion can be drawn from this observation?
- The reverse reaction in the equation is endothermic.
- The forward reaction in the equation is endothermic.
- The brown colour is due to the strong nitrogen–oxygen bonds in \(\ce{NO2}\).
- The equilibrium concentration of \( \ce{N2O4}\) is not dependent on temperature.
CHEMISTRY, M7 EQ-Bank 26
This flow chart shows reactions involving six different organic compounds (A to F).
Draw the structures of compounds A to F, justifying your diagrams with reference to the information provided. (7 marks)
--- 16 WORK AREA LINES (style=lined) ---
CHEMISTRY, M8 EQ-Bank 23
\(\ce{Fe^2^+}\) and \(\ce{X} \) react to form an ionic compound according to the general equation
\(\ce{aFe^2^+ + $b$(X)\rightleftharpoons [Fe_a(X)_b]^2^a^+}\)
where \(\ce{$a$}\) and \(\ce{$b$}\) are numbers representing the ratio in which \(\ce{Fe^2^+}\) and \(\ce{X} \) combine.
Spectrophotometry was used to determine the stoichiometric ratio between \(\ce{Fe^2^+}\) and \(\ce{X} \). To do this, eight 10 mL samples were prepared by reacting solutions of \(\ce{Fe^2^+}\) with solutions of \(\ce{X} \) in varying ratios. All \(\ce{Fe^2^+}\) and \(\ce{X} \) solutions had the same concentration. The absorbance of the samples is tabulated below.
- On the grid, construct a graph of absorbance against volume of \(\ce{Fe^2^+}\) solution from 0.00 mL to 6.00 mL, and draw TWO lines of best fit. (3 marks)
- The reaction proceeds according to the general equation
- \(\ce{aFe^2^+ + $b$X \rightleftharpoons [Fe_a(X)_b]^2^a^+}\).
- Find the values of \(\ce{$a$}\) and \(\ce{$b$}\) . Justify your answer with reference to the data given and the graph in part (a). (3 marks)
--- 8 WORK AREA LINES (style=lined) ---
CHEMISTRY, M8 EQ-Bank 28
Limestone \(\ce{(CaCO_3)}\) contributes to the hardness of water by releasing \(\ce{Ca^2^+}\) ions. The following chemical equation represents this reaction.
\(\ce{CaCO3($s$) + H_2O($l$) + CO_2($g$) \rightleftharpoons Ca^2^+($aq$) + 2HCO3^-($aq$)}\) \((\Delta H<0)\)
It has been suggested that heating water reduces its hardness.
Explain how this suggestion can be tested accurately, validly and reliably. (9 marks)
--- 30 WORK AREA LINES (style=lined) ---
CHEMISTRY, M5 EQ-Bank 12
An industrial plant makes ammonia from nitrogen gas and hydrogen gas. The reaction is exothermic.
The graph shows the adjustments made to increase the yield of ammonia.
Account for the changes in conditions that have shaped the graph during the time the system was observed. Include a relevant chemical equation in your answer. (5 marks)
PHYSICS, M5 EQ-Bank 29
A student used the following scale diagram to investigate orbital properties. The diagram shows a planet and two of its moons, \(V\) and \(W\). The distances between each of the moons and the planet are to scale while the sizes of the objects are not.
Complete the table to compare the orbital properties of Moon \(V\) and Moon \(W\). Show relevant calculations in the space below the table. (4 marks)
--- 0 WORK AREA LINES (style=lined) ---
\begin{array}{|l|c|c|c|}
\hline
\rule{0pt}{2.5ex} & \textit{Orbital radius} & \textit{Orbital period} & \textit{Orbital velocity}\\
& \text{(\(W\) relative to \(V\))} \rule[-1ex]{0pt}{0pt}& \text{(\(W\) relative to \(V\))} & \text{(\(W\) relative to \(V\))} \\
\hline
\rule{0pt}{3.5ex}\text{Quantitative}&\text{}&\text{}&\text{}\\
\text{comparison}\rule[-2ex]{0pt}{0pt}&\text{}&\text{}&\text{}\\
\hline
\rule{0pt}{3.5ex}\text{Qualitative}&\text{}&\text{}&\text{}\\
\text{comparison}\rule[-2ex]{0pt}{0pt}&\text{}&\text{}&\text{}\\
\hline
\end{array}
PHYSICS, M5 EQ-Bank 28
A bullet is fired vertically from the surface of Mars, at the escape velocity of Mars. Another bullet is fired vertically from the surface of Earth, at the escape velocity of Earth.
Neglecting air resistance, compare the energy transformations of the two bullets. (5 marks)
PHYSICS, M5 EQ-Bank 25
In the 1840s, French physicist, Hippolyte Fizeau performed an experiment to measure the speed of light. He shone an intense light source at a mirror 8 km away and broke up the light beam with a rotating cogwheel. He adjusted the speed of rotation of the wheel until the reflected light beam could no longer be seen returning through the gaps in the cogwheel.
The diagram shows a similar experiment. The cogwheel has 50 teeth and 50 gaps of the same width.
Explain why specific speeds of rotation of the cogwheel will completely block the returning light. Support your answer with calculations. (5 marks)
--- 13 WORK AREA LINES (style=lined) ---
- « Previous Page
- 1
- …
- 32
- 33
- 34
- 35
- 36
- …
- 82
- Next Page »