Aussie Maths & Science Teachers: Save your time with SmarterEd
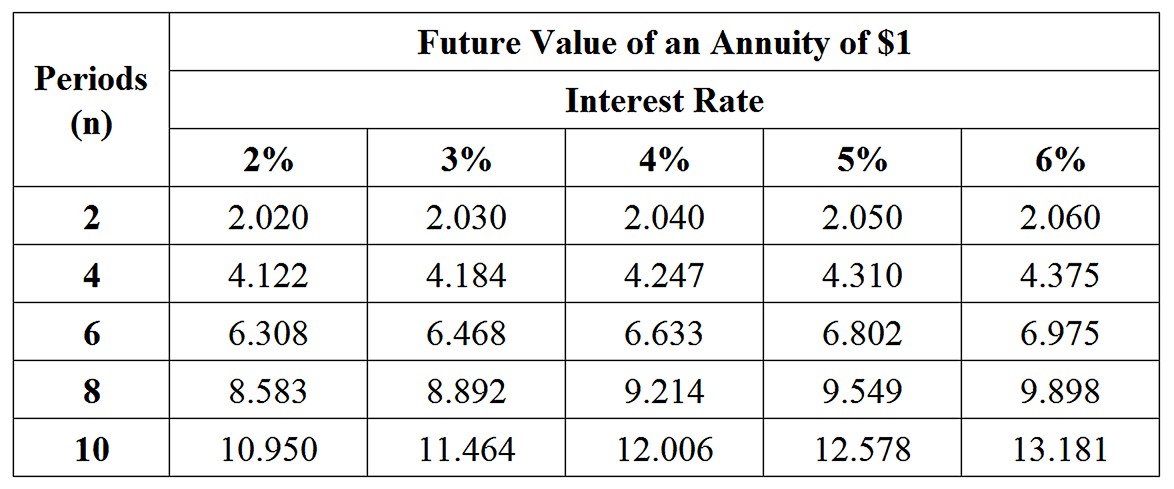
Leanne copied a two-way table into her book.
Leanne made an error in copying one of the values in the shaded section of the table.
Which value has been incorrectly copied?
Which of the following would be most likely to have a positive correlation?
Each student in a class is given a packet of lollies. The teacher records the number of red lollies in each packet using a frequency table.
What is the relative frequency of a packet of lollies containing more than three red lollies?
Dominique wants to save $15 000 to use as spending money when she travels overseas in 2 years' time.
If she invests $3500 at the end of every 6 months into an account earning 4% p.a., compounded half-yearly, will she have enough?
Use the table below to justify your answer. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Camilla buys a car for $21 000 and repays it over 4 years through equal monthly instalments.
She pays a 10% deposit and interest is charged at 9% p.a. on the reducing balance loan.
Using the Table of present value interest factors below, where `r` represents the monthly interest and `N` represents the number of repayments
--- 6 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
The following graph indicates `z`-scores of ‘height-for-age’ for girls aged 5 – 19 years.
--- 2 WORK AREA LINES (style=lined) ---
(1) If 2.5% of girls of the same age are taller than Rachel, how tall is she? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
(2) Rachel does not grow any taller. At age 15 ½, what percentage of girls of the same age will be taller than Rachel? (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
For adults (18 years and older), the Body Mass Index is given by
`B = m/h^2` where `m = text(mass)` in kilograms and `h = text(height)` in metres.
The medically accepted healthy range for `B` is `21 <= B <= 25`.
--- 4 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
(2) Give ONE reason why this equation is not suitable for predicting heights of girls older than 12. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
The graph shows the predicted population age distribution in Australia in 2008.
--- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
The retirement ages of two million people are displayed in a table.
--- 1 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
Cecil invited 175 movie critics to preview his new movie. After seeing the movie, he conducted a survey. Cecil has almost completed the two-way table.
--- 1 WORK AREA LINES (style=lined) ---
What is the probability that the critic was less than 40 years old and did not like the movie? (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Will this movie be considered a box office success? Justify your answer. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Christina has completed three Mathematics tests. Her mean mark is 72%.
What mark (out of 100) does she have to get in her next test to increase her mean mark to 73%? (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
In a survey, 450 people were asked about their favourite takeaway food. The results are displayed in the bar graph.
How many people chose pizza as their favourite takeaway food? (2 marks)
The diagram shows the position of `Q`, `R` and `T` relative to `P`.
In the diagram,
`Q` is south-west of `P`
`R` is north-west of `P`
`/_QPT` is 165°
What is the bearing of `T` from `P`?
`/_QPS=45^@\ \ \ text{(} Q\ text(is south west of)\ Ptext{)}`
`/_TPS = 165 – 45 = 120^@`
`:.\ /_NPT = 60^@\ \ text{(} 180^@\ text(in straight line) text{)}`
`=> A`
The height of each student in a class was measured and it was found that the mean height was 160 cm.
Two students were absent. When their heights were included in the data for the class, the mean height did not change.
Which of the following heights are possible for the two absent students?
A scatterplot is shown.
Which of the following best describes the correlation between \(R\) and \(T\)?
The marks for a Science test and a Mathematics test are presented in box-and-whisker plots.
Which measure must be the same for both tests?
What is the median of the following set of scores?
The stem-and-leaf plot represents the daily sales of soft drink from a vending machine.
| If the range of sales is 43, what is the value of |  |
? |
Simplify `2/n-1/(n+1)`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
The table below shows the present value of an annuity with a contribution of $1.
--- 2 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
Chris leaves island `A` in a boat and sails 142 km on a bearing of 078° to island `B`. Chris then sails on a bearing of 191° for 220 km to island `C`, as shown in the diagram.
--- 5 WORK AREA LINES (style=lined) ---
--- 7 WORK AREA LINES (style=lined) ---
| i. |  |
`text(Find)\ \ /_ABC`
`text(Let)\ D\ text(be south of)\ B`
`:.\ /_CBD = 191\ – 180 = 11°`
| `/_ DBA` | `= 78°\ text{(alternate)}` |
| `/_ ABC` | `= 78\ – 11` |
| `= 67°` |
`text(Using Cosine rule:)`
| `AC^2` | `= AB^2 + BC^2\ – 2 * AB * BC * cos /_ABC` |
| `= 142^2 + 220^2\ – 2 xx 142 xx 220 xx cos 67°` | |
| `= 44\ 151.119…` |
| `:.\ AC` | `= 210.121…` |
| `~~ 210\ text(km)\ \ \ text(… as required)` |
ii. `text(Find)\ \ /_ ACB`
`text(Using Sine rule:)`
| `(sin /_ ACB)/142` | `= (sin /_ABC)/210` |
| `sin /_ ACB` | `= (142 xx sin 67°)/210` |
| `= 0.6224…` | |
| `/_ ACB` | `= 38.494…` |
| `= 38°\ text{(nearest degree)}` |
`text(Let)\ E\ text(be due North of)\ C`
`/_ECB = 11°\ text{(} text(alternate to)\ /_CBD text{)}`
| `:.\ /_ECA` | `= 38\ – 11` |
| `= 27°` |
`:.\ text(Bearing of)\ A\ text(from)\ C`
`= 360\ – 27`
`= 333°`
The scatterplot shows the relationship between expenditure per primary school student, as a percentage of a country’s Gross Domestic Product (GDP), and the life expectancy in years for 15 countries.
--- 1 WORK AREA LINES (style=lined) ---
What is the interquartile range? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
Would this country be an outlier for this set of data? Justify your answer with calculations. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
`text(correlation between the two variables.)`
`text(of 127.3. This line of best fit is only accurate)`
`text(in a lower range of GDP expediture.)`
| i. | `text(It indicates there is a strong positive)` |
| `text(correlation between the two variables)` |
| ii. | `text(IQR)` | `= Q_U\ – Q_L` |
| `= 22.5\ – 8.4` | ||
| `= 14.1` |
iii. `text(An outlier on the upper side must be more than)`
`Q_u\ +1.5xxIQR`
`=22.5+(1.5xx14.1)`
`=\ text(43.65%)`
`:.\ text(A country with an expenditure of 47.6% is an outlier).`
| iv. | |
v. `text(Life expectancy) ~~ 73.1\ text{years (see dotted line)}`
`text(Alternative Solution)`
`text(When)\ x=18`
`y=1.29(18)+49.9=73.12\ \ text(years)`
| vi. | `text(At 60% GDP, the line predicts a life)` |
| `text(expectancy of 127.3. This line of best)` | |
| `text(fit is only predictive in a lower range)` | |
| `text(of GDP expenditure.)` |
Chandra and Sascha plan to have $20 000 in an investment account in 15 years time for their grandchild’s university fees.
The interest rate for the investment account will be fixed at 3% per annum compounded monthly.
Calculate the amount that they will need to deposit into the account now in order to achieve their plan. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Terry and Kim each sat twenty class tests. Terry’s results on the tests are displayed in the box-and-whisker plot shown in part (i).
Draw a box-and-whisker plot to display Kim’s results below that of Terry’s results. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
Justify your answer by referring to the summary statistics and the skewness of the distributions. (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
| i. |  |
ii. `text(50%)`
iii. `text(Terry’s results are more positively skewed than)`
`text(Kim’s and also have a higher limit high.)`
`text(However, Kim’s results are more consistent,)`
`text(showing a tighter IQR. They also have a)`
`text(significantly higher median than Terry’s and)`
`text(are evenly skewed.)`
`:.\ text(Kim’s results were better.)`
The times taken for 160 music downloads were recorded, grouped into classes and then displayed using the cumulative frequency histogram shown.
On the diagram, draw the lines that are needed to find the median download time. (2 marks)
--- 0 WORK AREA LINES (style=lined) ---
Solve the equation `(5x + 1)/3-4 = 5-7x`. (3 marks)
The weights of 10 000 newborn babies in NSW are normally distributed. These weights have a mean of 3.1 kg and a standard deviation of 0.35 kg.
How many of these newborn babies have a weight between 2.75 kg and 4.15 kg?
The following information is given about the locations of three towns `X`, `Y` and `Z`:
• `X` is due east of `Z`
• `X` is on a bearing of 145° from `Y`
• `Y` is on a bearing of 060° from `Z`.
Which diagram best represents this information?
`text(S)text(ince)\ X\ text(is due east of)\ Z`
`=> text(Cannot be)\ B\ text(or)\ D`
`text(The diagram shows we can find)`
`/_ZYX = 60 + 35^@ = 95^@`
`text(Using alternate angles)\ (60^@)\ text(and)`
`text(the)\ 145^@\ text(bearing of)\ X\ text(from)\ Y`
`=> C`
A table of future value interest factors is shown.
A certain annuity involves making equal contributions of $25 000 into an account every 6 months for 2 years at an interest rate of 4% per annum.
Based on the information provided, what is the future value of this annuity?
Twenty Year 12 students were surveyed. These students were asked how many hours of sport they play per week, to the nearest hour.
The results are shown in the frequency table.
\begin{array} {|c|c|}
\hline
\rule{0pt}{2.5ex} \textit{Hours per week} \rule[-1ex]{0pt}{0pt} & \ \ \ \ \ \textit{Frequency}\ \ \ \ \ \\
\hline
\rule{0pt}{2.5ex} \text{0 – 2} \rule[-1ex]{0pt}{0pt} & 5 \\
\hline
\rule{0pt}{2.5ex} \text{3 – 5} \rule[-1ex]{0pt}{0pt} & 10 \\
\hline
\rule{0pt}{2.5ex} \text{6 – 8} \rule[-1ex]{0pt}{0pt} & 3 \\
\hline
\rule{0pt}{2.5ex} \text{9 – 11} \rule[-1ex]{0pt}{0pt} & 2 \\
\hline
\end{array}
What is the mean number of hours of sport played by the students per week?
A group of 150 people was surveyed and the results recorded.
A person is selected at random from the surveyed group.
What is the probability that the person selected is a male who does not own a mobile?
Sketch the graph of `y-2x = 3`, showing the intercepts on both axes. (2 marks)
--- 8 WORK AREA LINES (style=lined) ---
`y-2x=3\ \ =>\ \ y=2x+3`
`ytext{-intercept}\ = 3`
`text{Find}\ x\ text{when}\ y=0:`
`0-2x=3\ \ =>\ \ x=-3/2`
Josephine invests $50 000 for 15 years, at an interest rate of 6% per annum, compounded annually.
Emma invests $500 at the end of each month for 15 years, at an interest rate of 6% per annum, compounded monthly.
Financial gain is defined as the difference between the final value of an investment and the total contributions.
Who will have the better financial gain after 15 years? Using the Table below* and appropriate formulas, justify your answer with suitable calculations. (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
Two brands of light bulbs are being compared. For each brand, the life of the light bulbs is normally distributed.
What is the `z`-score of the life of this light bulb? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
‘Brand A light bulbs are more likely to be defective than Brand B light bulbs.’
Is this claim correct? Justify your answer, with reference to `z`-scores or standard deviations or the normal distribution. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Data was collected from 30 students on the number of text messages they had sent in the previous 24 hours. The set of data collected is displayed.
--- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
At another school, students who use mobile phones were surveyed. The set of data is shown in the table.
--- 1 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
Ten new male students are surveyed and all ten are on a plan. The set of data is updated to include this information.
--- 2 WORK AREA LINES (style=lined) ---
The graph below displays data collected at a school on the number of students
in each Year group, who own a mobile phone.
--- 1 WORK AREA LINES (style=lined) ---
Which student is more likely to own a mobile phone?
Justify your answer with suitable calculations. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
A study on the mobile phone usage of NSW high school students is to be conducted.
Data is to be gathered using a questionnaire.
The questionnaire begins with the three questions shown.
--- 1 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
Describe a method that could be used to obtain a representative stratified sample. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
An amount of $5000 is invested at 10% per annum, compounded six-monthly.
Use the table to find the value of this investment at the end of three years. (2 marks)
The graph shows tax payable against taxable income, in thousands of dollars.
--- 1 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
| i. |  |
`text(Income on)\ $21\ 000=$3000\ \ \ text{(from graph)}`
ii. `text(Using the points)\ (21,3)\ text(and)\ (39,9)`
| `text(Gradient at)\ A` | `= (y_2\-y_1)/(x_2\ -x_1)` |
| `= (9000-3000)/(39\ 000 -21\ 000)` | |
| `= 6000/(18\ 000)` | |
| `= 1/3\ \ \ \ \ text(… as required)` |
iii. `text(The gradient represents the tax applicable to each dollar)`
| `text(Tax)` | ` = 1/3\ text(of each dollar earned)` |
| ` = 33 1/3\ text(cents per dollar earned)` |
iv. `text( Tax payable up to $21 000 = $3000)`
`text(Tax payable on income between $21 000 and $39 000)`
` = 1/3 (I\-21\ 000)`
| `:.\ text(Tax payable on)\ \ I` | `= 3000 + 1/3 (I\-21\ 000)` |
| `= 3000 + 1/3 I\-7000` | |
| `= 1/3 I\-4000` |
The graphs show the distribution of the ages of children in Numbertown in 2000 and 2010.
How many children were aged 12–18 years in 2000? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
How many children aged 0–18 years are there in 2010? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
A new shopping centre has opened near a primary school. A survey is conducted to determine the number of motor vehicles that pass the school each afternoon between 2.30 pm and 4.00 pm.
The results for 60 days have been recorded in the table and are displayed in the cumulative frequency histogram.
--- 1 WORK AREA LINES (style=lined) ---
What problem could arise from the change in the median number of motor vehicles passing the school before and after the opening of the new shopping centre?
Briefly recommend a solution to this problem. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
`text(Solutions)`
| i. | `X` | `= 25\ -10` |
| `= 15` |
| ii. | |
iii. `text(Median)\ ~~155`
| iv. | `text(Problems)` |
| `text(- increased traffic delays)` | |
| `text(- increased danger to students leaving school)` | |
| `text(Solutions)` | |
| `text(- signpost alternative routes around school)` | |
| `text(- decrease the speed limit in the area)` |
A die was rolled 72 times. The results for this experiment are shown in the table.
\begin{array} {|c|c|}
\hline
\rule{0pt}{2.5ex} \textit{Number obtained} \rule[-1ex]{0pt}{0pt} & \textit{Frequency} \\
\hline
\rule{0pt}{2.5ex} \ 1 \rule[-1ex]{0pt}{0pt} & 16 \\
\hline
\rule{0pt}{2.5ex} \ 2 \rule[-1ex]{0pt}{0pt} & 11 \\
\hline
\rule{0pt}{2.5ex} \ 3 \rule[-1ex]{0pt}{0pt} & \textbf{A} \\
\hline
\rule{0pt}{2.5ex} \ 4 \rule[-1ex]{0pt}{0pt} & 8 \\
\hline
\rule{0pt}{2.5ex} \ 5 \rule[-1ex]{0pt}{0pt} & 12 \\
\hline
\rule{0pt}{2.5ex} \ 6 \rule[-1ex]{0pt}{0pt} & 15 \\
\hline
\end{array}
--- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
A function centre hosts events for up to 500 people. The cost `C`, in dollars, for the centre
to host an event, where `x` people attend, is given by:
`C = 10\ 000 + 50x`
The centre charges $100 per person. Its income `I`, in dollars, is given by:
`I = 100x`
How much greater is the income of the function centre when 500 people attend an event, than its income at the breakeven point?
The heights of the players in a basketball team were recorded as 1.8 m, 1.83 m, 1.84 m, 1.86 m and 1.92 m. When a sixth player joined the team, the average height of the players increased by 1 centimetre.
What was the height of the sixth player?
A data set of nine scores has a median of 7.
The scores 6, 6, 12 and 17 are added to this data set.
What is the median of the data set now?
The table shows the future value of a $1 annuity at different interest rates over different numbers of time periods.
--- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
In an experiment, two unbiased dice, with faces numbered 1, 2, 3, 4, 5, 6 are rolled 18 times.
The difference between the numbers on their uppermost faces is recorded each time. Juan performs this experiment twice and his results are shown in the tables.
Juan states that Experiment 2 has given results that are closer to what he expected than the results given by Experiment 1.
Is he correct? Explain your answer by finding the sample space for the dice differences and using theoretical probability. (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
`text(Sample space for dice differences)`
`text(Juan is correct. The table shows Experiment 1)`
`text(has greater total differences to the expected)`
`text(frequencies than Experiment 2)`
The height and mass of a child are measured and recorded over its first two years.
\begin{array} {|l|c|c|}
\hline \rule{0pt}{2.5ex} \text{Height (cm), } H \rule[-1ex]{0pt}{0pt} & \text{45} & \text{50} & \text{55} & \text{60} & \text{65} & \text{70} & \text{75} & \text{80} \\
\hline \rule{0pt}{2.5ex} \text{Mass (kg), } M \rule[-1ex]{0pt}{0pt} & \text{2.3} & \text{3.8} & \text{4.7} & \text{6.2} & \text{7.1} & \text{7.8} & \text{8.8} & \text{10.2} \\
\hline
\end{array}
This information is displayed in a scatter graph.
--- 2 WORK AREA LINES (style=lined) ---
Find the equation of this line. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
A yacht race follows the triangular course shown in the diagram. The course from `P` to `Q` is 1.8 km on a true bearing of 058°.
At `Q` the course changes direction. The course from `Q` to `R` is 2.7 km and `/_PQR = 74^@`.
--- 1 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
What is the area of this ‘no-go’ zone? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
| i. |  |
`/_ PQS = 58^@ \ \ \ (text(alternate to)\ /_TPQ)`
`text(Bearing of)\ R\ text(from)\ Q`
| `= 180^@ + 58^@ + 74^@` |
| `= 312^@` |
ii. `text(Using Cosine rule:)`
| `RP^2` | `=RQ^2` + `PQ^2` `- 2` `xx RQ` `xx PQ` `xx cos` `/_RQP` |
| `= 2.7^2` + `1.8^2` `- 2` `xx 2.7` `xx 1.8` `xx cos74^@` | |
| `=7.29 + 3.24\ – 2.679…` | |
| `=7.851…` |
| `:.RP` | `= sqrt(7.851…)` |
| `=2.8019…` | |
| `~~ 2.8\ text(km) (text(1 d.p.) )` |
iii. `text(Using)\ \ A = 1/2 ab sinC`
| `A` | `= 1/2` `xx 2.7` `xx 1.8` `xx sin74^@` |
| `= 2.3358…` | |
| `= 2.3\ text(km²)` |
`:.\ text(No-go zone is 2.3 km²)`
In a school, boys and girls were surveyed about the time they usually spend on the internet over a weekend. These results were displayed in box-and-whisker plots, as shown below.
--- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
Under what circumstances would this statement be true? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
In Broken Hill, the maximum temperature for each day has been recorded. The mean of these maximum temperatures during spring is 25.8°C, and their standard deviation is 4.2° C.
--- 1 WORK AREA LINES (style=lined) ---
You may assume that these maximum temperatures are normally distributed and that
• 68% of maximum temperatures have `z`-scores between –1 and 1
• 95% of maximum temperatures have `z`-scores between –2 and 2
• 99.7% of maximum temperatures have `z`-scores between –3 and 3. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Ali’s class sits two Geography tests. The results of her class on the first Geography test are shown.
`58,\ \ 74,\ \ 65,\ \ 66,\ \ 73,\ \ 71,\ \ 72,\ \ 74,\ \ 62,\ \ 70`
The mean was 68.5 for the first test.
--- 1 WORK AREA LINES (style=lined) ---
Ali scored 62 on the first test. Calculate the mark that she needed to obtain in the second test to ensure that her performance relative to the class was maintained. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Ahmed collected data on the age (`a`) and height (`h`) of males aged 11 to 16 years.
He created a scatterplot of the data and constructed a line of best fit to model the relationship between the age and height of males.
--- 2 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
A retailer has collected data on the number of televisions that he sold each week in 2012.
He grouped the data into classes and displayed the data using a cumulative frequency histogram and polygon (ogive).
--- 4 WORK AREA LINES (style=lined) ---
Is he correct? Give a reason for your answer. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
Kimberley has invested $3500.
Interest is compounded half-yearly at a rate of 2% per half-year.
Use the table to calculate the value of her investment at the end of 4 years. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Write down a set of six data values that has a range of 12, a mode of 12 and a minimum value of 12. (2 marks)
The marks in a class test are normally distributed. The mean is 100 and the standard deviation is 10.
--- 1 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
You may assume the following:
• 68% of marks have a `z`-score between –1 and 1
• 95% of marks have a `z`-score between –2 and 2
• 99.7% of marks have a `z`-score between –3 and 3. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
On Saturday, Jonty recorded the colour of T-shirts worn by the people at his gym. The results are shown in the graph.
--- 1 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
A factory makes boots and sandals. In any week
• the total number of pairs of boots and sandals that are made is 200
• the maximum number of pairs of boots made is 120
• the maximum number of pairs of sandals made is 150.
The factory manager has drawn a graph to show the numbers of pairs of boots (`x`) and sandals (`y`) that can be made.
--- 2 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
Compare the profits at `B` and `C`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
The Australian Bureau of Statistics provides the NSW government with data on the age of residents living in different areas across the state. After analysing this data, the government makes decisions relating to the provision of services or facilities.
Give an example of a possible decision the government might make and describe how the data might justify this decision. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
