SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

CHEMISTRY, M7 2024 HSC 24

The boiling points for two series of compounds are listed.

 

  1. Plot the boiling points for each series of compounds against the number of carbon atoms per molecule.   (3 marks)

  1. With reference to hydrogen bonding and dispersion forces, explain the trends in the boiling point data of these compounds, within each series and between the series.   (4 marks)

Show Answers Only

a.     

b.     The alcohols have higher boiling points than amines of the same chain length.

  • Both alcohols and amines have polar hydrogen bonding as a result of the \(\ce{OH}\) and \(\ce{NH2}\) functional groups respectively.
  • Oxygen molecules have higher electronegativity than nitrogen molecules making the hydrogen bonding in the alcohols significantly stronger than the hydrogen bonding in amines.
  • Since the dispersion forces in amines and alcohols of the same chain length are very similar, the difference in the strength of the intermolecular bonding is dependent on the strength of the hydrogen bonding.
  • Therefore, a larger amount of thermal energy is required to separate the alcohol molecules resulting in higher boiling points than amines. 

As the chain length of the alcohols and amines increase, the boiling points also increase.

  • When the chain length increases, the number of electrons in the molecules also increase which corresponds to a larger number of dispersion forces between neighbouring molecules.
  • The stronger dispersion forces between the molecules increase the overall strength of the intermolecular forces in both the alcohols and amines therefore leading to higher boiling points as chain length increases.

Show Worked Solution

a.   

       
 

b.     The alcohols have higher boiling points than amines of the same chain length.

  • Both alcohols and amines have polar hydrogen bonding as a result of the \(\ce{OH}\) and \(\ce{NH2}\) functional groups respectively.
  • Oxygen molecules have higher electronegativity than nitrogen molecules making the hydrogen bonding in the alcohols significantly stronger than the hydrogen bonding in amines.
  • Since the dispersion forces in amines and alcohols of the same chain length are very similar, the difference in the strength of the intermolecular bonding is dependent on the strength of the hydrogen bonding.
  • Therefore, a larger amount of thermal energy is required to separate the alcohol molecules resulting in higher boiling points than amines.

As the chain length of the alcohols and amines increase, the boiling points also increase.

  • When the chain length increases, the number of electrons in the molecules also increase which corresponds to a larger number of dispersion forces between neighbouring molecules.
  • The stronger dispersion forces between the molecules increase the overall strength of the intermolecular forces in both the alcohols and amines therefore leading to higher boiling points as chain length increases.

Networks, GEN2 2024 VCAA 14

A manufacturer \((M)\) makes deliveries to the supermarket \((S)\) via a number of storage warehouses, \(L, N, O, P, Q\) and \(R\). These eight locations are represented as vertices in the network below.

The numbers on the edges represent the maximum number of deliveries that can be made between these locations each day.
 

  1. When considering the possible flow of deliveries through this network, many different cuts can be made.   
  2. Determine the capacity of Cut 1, shown above.   (1 mark)

  3. Determine the maximum number of deliveries that can be made each day from the manufacturer to the supermarket.   (1 mark)

  4. The manufacturer wants to increase the number of deliveries to the supermarket.
  5. This can be achieved by increasing the number of deliveries between one pair of locations.
  6. Complete the following sentence by writing the locations on the lines provided:
  7. To maximise this increase, the number of deliveries should be increased between
    locations ____ and  ____.       (1 mark)

    

Show Answers Only

a.    \(46\)

b.    \(37\)

c.    \(\text{R and S}\)

Show Worked Solution

a.    \(13+18+6+9=46\)

\(\text{(Reverse flow}\ Q → O\ \text{is not counted.)}\)
 

b.  

\(\text{Max deliveries (min cut)}\ =13+5+11+8=37\)

♦ Mean mark (b) 29%.

 
c.   \(\text{The number of deliveries should be increased between}\)

\(\text{locations R and S.}\)

♦ Mean mark (c) 22%.

CHEMISTRY, M6 2024 HSC 21

A solution of acetic acid reacts with magnesium metal.

Write the names of the products of this reaction in the boxes provided.   (2 marks)

Show Answers Only

  • Products: hydrogen gas \(\ce{H2(g)}\) and magnesium acetate/ethanoate \(\ce{Mg(CH3COO)2(aq)}\)

Show Worked Solution

  • Acid + active metal \(\ce{->}\) hydrogen + salt
  • Products: hydrogen gas \(\ce{H2(g)}\) and magnesium acetate/ethanoate \(\ce{Mg(CH3COO)2(aq)}\)

CHEMISTRY, M5 2024 HSC 10 MC

The following system is at equilibrium.

\(\underset{\text { propan-2-ol }}{\ce{CH_3CHOHCH_3(g)}} \rightleftharpoons \underset{\text {propan-2-one}}{\ce{CH_3COCH_3(g)}}\)\(\ce{+ H_2(g)}\)

A catalyst is added to the system.

Which row of the table correctly identifies the change in the yield of propan-2-one and the reaction rates?

\begin{align*}
\begin{array}{l}
\ & \\
\\
\textbf{A.}\\
\\
\textbf{B.}\\
\\
\textbf{C.}\\
\\
\textbf{D.}\\
\\
\end{array}
\begin{array}{|l|l|}
\hline
\quad\quad \textit{Yield of } & \quad \quad \quad \quad \textit{Reaction Rates} \\
\quad\textit{propan-2-one} & \textit{} \\
\hline
\text{Remains the same} & \text{Both forward and reverse rates} \\
\text{} & \text{are unchanged.} \\
\hline
\text{Remains the same} & \text{Both forward and reverse rates} \\
\text{} & \text{increase equally} \\
\hline
\text{Decreases} & \text{Reverse rate increases more than} \\
\text{} & \text{the forward rate increases.} \\
\hline
\text{Increases} & \text{Forward rate increases more than}\\
\text{} & \text{the reverse rate increases.}\\
\hline
\end{array}
\end{align*}

Show Answers Only

\(B\)

Show Worked Solution
  • Adding a catalyst to an equilibrium system will decrease the activation energy of both the forward and reverse reactions equally.
  • Thus, the reaction rate of the forward and reverse reactions will both increase and cause no change to the yield of the reaction.

\(\Rightarrow B\)

CHEMISTRY, M8 2024 HSC 9 MC

Which of the following is the mass spectrum of ethanamine?
 

 

Show Answers Only

\(B\)

Show Worked Solution
  • The molar mass of ethanamine, \(\ce{CH3CH2NH2}\), is 45.086 g mol\(^{-1}\)
  • The peak with the largest mass to charge ratio displays the molar mass of the substance.
  • Therefore, the parent ion peak will be at 45.

\(\Rightarrow B\)

CHEMISTRY, M8 2024 HSC 8 MC

Which pair of ions produce different colours in a flame test?

  1. \(\ce{Br^{-} and Cl^{-}}\)
  2. \(\ce{Ag^{+} and OH^{-}}\)
  3. \(\ce{Cu^{2+} and Ca^{2+}}\)
  4. \(\ce{CH_3OOO^{-} and H_2 PO_4^{-}}\)
Show Answers Only

\(C\)

Show Worked Solution
  • Only metal cations produce unique colours during a flame test due to their electron configurations.
  • As the electrons ‘fall back’ down into their shells from an excited state, they emit a specific light wave (colour).

\(\Rightarrow C\)

CHEMISTRY, M8 2024 HSC 4 MC

An infrared spectrum of an organic compound is shown.
 

     

Which of the following compounds would produce the spectrum shown?
 

Show Answers Only

\(A\)

Show Worked Solution
  • The broad absorption peak between 3500 to 3250 indicates the presence of an \(\ce{O-H}\) alcohol group.

\(\Rightarrow A\)

Networks, GEN2 2024 VCAA 13

A supermarket has five departments, with areas allocated as shown on the floorplan below.
 

The floorplan is represented by the graph below.

On this graph, vertices represent departments and edges represent boundaries between two departments.

This graph is incomplete.
 

  1. Draw the missing vertex and missing edges on the graph above. Include a label.   (1 mark)

Karla is standing in the Promotional department.

She wants to visit each department in the supermarket once only.

  1.  i.  In which department will she finish?  (1 mark)
  2. ii.  What is the mathematical name for this type of journey?  (1 mark)
  3. The supermarket adds a new Entertainment department \((E)\), and the floorplan is rearranged.
  4. The boundaries between the departments are represented in the adjacency matrix below, where a ' 1 ' indicates a boundary between the departments.

\begin{aligned}
& \ \ B \ \ \ D \ \ \  E \ \ \  F \ \ \ G \ \ \ P \\
\begin{array}{c}
B\\
D \\
E \\
F \\
G \\
P
\end{array}& \begin{bmatrix}
0 & 1 & 1 & 1 & 0 & 1 \\
1 & 0 & 0 & 1 & 1 & 0 \\
1 & 0 & 0 & 0 & 0 & 1 \\
1 & 1 & 0 & 0 & 1 & 1 \\
0 & 1 & 0 & 1 & 0 & 1 \\
1 & 0 & 1 & 1 & 1 & 0
\end{bmatrix}
\end{aligned}

  1. Use the adjacency matrix to complete the floorplan below by labelling each department. The Bakery \((B)\) is already labelled.  (1 mark)

Show Answers Only

a. 

 
b.i.   \(\text{The bakery}\)

b.ii.  \(\text{Hamiltonian Path}\)
 

c.

Show Worked Solution

a. 

b.i.  \(\text{Bakery}\)

b.ii. \(\text{The path has no repeated edges or vertices, and }\)

\(\text{incudes all the edges of the graph.}\)

\(\therefore\ \text{It is a Hamiltonian Path.}\)

c.

Matrices, GEN2 2024 VCAA 9

Vince works on a construction site.

The amount Vince gets paid depends on the type of shift he works, as shown in the table below.

\begin{array}{|l|c|c|c|}
\hline
\rule{0pt}{2.5ex} \textbf{Shift type} \rule[-1ex]{0pt}{0pt}& \textbf{Normal} & \textbf{Overtime} & \textbf {Weekend} \\
\hline
\rule{0pt}{2.5ex} \textbf{Hourly rate of pay} \rule[-1ex]{0pt}{0pt} \ \text{(\$ per hour)} & 36 & 54 & 72 \\
\hline
\end{array}

This information is shown in matrix \(R\) below.

\begin{align*}
R=\left[\begin{array}{lll}
36 & 54 & 72
\end{array}\right] \end{align*}

  1. Matrix \(R^T\) is the transpose of matrix \(R\).
  2. Determine the matrix \(R^T\).   (1 mark)

During one week, Vince works 28 hours at the normal rate of pay, 6 hours at the overtime rate of pay, and 8 hours at the weekend rate of pay.

  1. Complete the following matrix calculation showing the total amount Vince has been paid for this week.  (1 mark)

  

Vince will receive $90 per hour if he works a public holiday shift.

Matrix \(Q\), as calculated below, can be used to show Vince's hourly rate for each type of shift.

\begin{align*}
\begin{aligned}
Q & =n \times\left[\begin{array}{llll}
1 & 1.5 & 2 & p
\end{array}\right] \\
& =\left[\begin{array}{llll}
36 & 54 & 72 & 90
\end{array}\right] \end{aligned}
\end{align*}

  1. Write the values of \(n\) and \(p\).  (1 mark)

Show Answers Only

a.   \(R^T=\begin{bmatrix}
36 \\
54 \\
72
\end{bmatrix}\)

b.    \([28\quad  6\quad  8]\times R^T = [1908]\)

c.    \(n=36\ ,\ p=2.5\)

Show Worked Solution

a.   \(R^T=\begin{bmatrix}
36 \\
54 \\
72
\end{bmatrix}\)

 
b.    \(\begin{bmatrix}
28 & 6 & 8
\end{bmatrix}\times\ R^T=\begin{bmatrix}
28\times36 + 6\times54+ 8\times 72
\end{bmatrix}=[1908]\)

 
c.   \(n=\ \text{Normal hourly rate}\ =36\)

\(p=\ \text{Overtime rate}\ =\dfrac{90}{36}=2.5\)

Financial Maths, GEN2 2024 VCAA 5

Emi operates a mobile dog-grooming business.

The value of her grooming equipment will depreciate.

Based on average usage, a rule for the value, in dollars, of the equipment, \(V_n\), after \(n\) weeks is

\(V_n=15000-60 n\)

Assume that there are exactly 52 weeks in a year.

  1. By what amount, in dollars, does the value of the grooming equipment depreciate each week?   (1 mark)

  2. Emi plans to replace the grooming equipment after four years.   
  3. What will be its value, in dollars, at this time?   (1 mark)

  4. \(V_n\) is the value of the grooming equipment, in dollars, after \(n\) weeks.   
  5. Write a recurrence relation in terms of \(V_0, V_{n+1}\) and \(V_n\) that can model this value from one week to the next.   (1 mark)

  6. The value of the grooming equipment decreases from one year to the next by the same percentage of the original $15 000 value.
  7. What is this annual flat rate percentage?   (1 mark)

Show Answers Only

a.    \($60\)

b.    \($2520\)

c.    \(V_0=15\,000 , \ \ V_{n+1}=V_n-60\)

d.    \(20.8\%\)

Show Worked Solution

a.    \($60\)
 

b.    \(n=4\times 52=208\)

\(V_{208}\) \(=15\,000-60\times208\)
  \(=$2520\)

 
c.    \(V_0=15\,000 , \ \ V_{n+1}=V_n-60\)
 

d.    \(\text{Flat rate}\ =\dfrac{60}{15\,000}\times 52\times 100\%=20.8\%\)

♦ Mean mark (d) 42%.

Data Analysis, GEN2 2024 VCAA 3

The Olympic gold medal-winning height for the women's high jump, \(\textit{Wgold}\), is often lower than the best height achieved in other international women's high jump competitions in that same year.

The table below lists the Olympic year, \(\textit{year}\), the gold medal-winning height, \(\textit{Wgold}\), in metres, and the best height achieved in all international women's high jump competitions in that same year, \(\textit{Wbest}\), in metres, for each Olympic year from 1972 to 2020.

A scatterplot of \(\textit{Wbest}\) versus \(\textit{Wgold}\) for this data is also provided.

When a least squares line is fitted to the scatterplot, the equation is found to be:

\(Wbest =0.300+0.860 \times Wgold\)

The correlation coefficient is 0.9318

  1. Name the response variable in this equation.   (1 mark)

  2. Draw the least squares line on the scatterplot above.  (1 mark)

  3. Determine the value of the coefficient of determination as a percentage.  (1 mark)
  4. Round your answer to one decimal place.
  5. Describe the association between \(\textit{Wbest}\) and \(\textit{Wgold}\) in terms of strength and direction.  (1 mark)

\begin{array}{|l|l|}
\hline
\rule{0pt}{2.5ex}\text { strength } \rule[-1ex]{0pt}{0pt} & \quad \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\\
\hline
\rule{0pt}{2.5ex}\text { direction } \rule[-1ex]{0pt}{0pt} & \\
\hline
\end{array}

  1. Referring to the equation of the least squares line, interpret the value of the slope in terms of the variables \(\textit{Wbest}\) and \(\textit{Wgold}\).  (1 mark)

  2. In 1984, the \(\textit{Wbest}\) value was 2.07 m for a \(\textit{Wgold}\) value of 2.02 m .
  3. Show that when this least squares line is fitted to the scatterplot, the residual value for this point is 0.0328.  (2 marks)

  4. The residual plot obtained when the least squares line was fitted to the data is shown below. The residual value from part f is missing from the residual plot.
     

    1. Complete the residual plot by adding the residual value from part f, drawn as a cross ( X ), to the residual plot above.   (1 mark)

    2. In part b, a least squares line was fitted to the scatterplot. Does the residual plot from part g justify this? Briefly explain your answer.  (1 mark)

  1. In 1964, the gold medal-winning height, \(\textit{Wgold}\), was 1.90m . When the least squares line is used to predict \(\textit{Wbest}\), it is found to be 1.934 m .
  2. Explain why this prediction is not likely to be reliable.  (1 mark)

Show Answers Only

a.    \(Wbest\)

b.    

c.    \(86.8\%\)

d.    \(\text{Strong, positive}\)

e.    \(Wbest\ \text{will increase, on average, by 0.86 metres for every metre of increase in}\ Wgold.\)

f.      \(Wbest\) \(=0.300 +0.86\times 2.02\)
    \(=2.0372\)

\(\therefore\ \text{Residual}\ =2.07-2.0372=0.0328\)

g.i.

g.ii.  \(\text{Yes, it is justified as there is no clear pattern, linear or otherwise.}\)

h.    \(\text{This prediction is outside the data range (1972 – 2020 → extrapolation)}\)

\(\text{and therefore cannot be relied upon.}\)

Show Worked Solution

a.    \(Wbest\)

b.    \(\text{Using points:}\ (1.90, 1.934)\ \text{and}\ (2.00, 2.02)\)
 

Mean mark (b) 51%.

c.    \(r=0.9318\ \ \Rightarrow\ \ r^2=0.9318^2=0.8682\dots\)

\(\therefore\ \text{Coefficient of determination} \approx 86.8\%\)
 

d.    \(\text{Strong, positive}\)
 

e.    \(Wbest\ \text{will increase, on average, by 0.86 metres for every metre of increase in}\ Wgold.\)
 

f.      \(Wbest\) \(=0.300 +0.86\times 2.02\)
    \(=2.0372\)

 
\(\therefore\ \text{Residual}\ =2.07-2.0372=0.0328\)

♦ Mean mark (f) 48%.

g.i.

g.ii.  \(\text{Yes, it is justified as there is no clear pattern, linear or otherwise.}\)

♦ Mean mark (g)(i) 47%.
♦ Mean mark (g)(ii) 40%.

h.    \(\text{This prediction is outside the data range (1972–2020 → extrapolation)}\)

\(\text{and therefore cannot be relied upon.}\)

♦ Mean mark (h) 50%.

Data Analysis, GEN2 2024 VCAA 2

The boxplot below displays the distribution of all gold medal-winning heights for the women's high jump, \(\textit{Wgold}\), in metres, for the 19 Olympic Games held from 1948 to 2020.

  1. Describe the shape of this data distribution.   (1 mark)

  2. For this boxplot, what is the smallest possible number of \(\textit{Wgold}\) heights lower than 1.85 m?   (1 mark)

  3.  i. Using the boxplot, show that the lower fence is 1.565 m and the upper fence is 2.325 m.  (1 mark)

  4. ii. Referring to the boxplot, the lower fence and the upper fence, explain why no outliers exist.  (1 mark)

Show Answers Only

a.    \(\text{Negatively skewed}\)

b.    \(1\)

c.i.  \(Q_1=1.85,\ Q_3=2.04,\ IQR=2.04-1.85=0.19\)

\(\text{Lower Fence}\) \(=Q_1-1.5\times IQR\)
  \(=1.85-1.5\times 0.19\)
  \(=1.565\)
\(\text{Upper Fence}\) \(=Q_1+1.5\times IQR\)
  \(=2.04+1.5\times 0.19\)
  \(=2.325\)

c.ii. \(\text{No values exist below the lower fence or above the upper fence.}\)

\(\therefore\ \text{No outliers exist.}\)

Show Worked Solution

a.    \(\text{Negatively skewed.}\)
 

b.    \(\text{Only 1 value is needed to extend the whisker below the}\)

\(\text{range of the}\ IQR.\)

♦♦♦ Mean mark (b) 3%.

c.i.  \(Q_1=1.85,\ Q_3=2.04,\ IQR=2.04-1.85=0.19\)

\(\text{Lower Fence}\) \(=Q_1-1.5\times IQR\)
  \(=1.85-1.5\times 0.19\)
  \(=1.565\)
\(\text{Upper Fence}\) \(=Q_1+1.5\times IQR\)
  \(=2.04+1.5\times 0.19\)
  \(=2.325\)

   

c.ii. \(\text{No values exist below the lower fence or above the upper fence.}\)

\(\therefore\ \text{No outliers exist.}\)

Data Analysis, GEN2 2024 VCAA 1

Table 1 lists the Olympic year, \(\textit{year}\), and the gold medal-winning height for the men's high jump, \(\textit{Mgold}\), in metres, for each Olympic Games held from 1928 to 2020. No Olympic Games were held in 1940 or 1944, and the 2020 Olympic Games were held in 2021.

Table 1

\begin{array}{|c|c|}
\hline \quad \textit{year} \quad & \textit{Mgold}\,\text{(m)} \\
\hline 1928 & 1.94 \\
\hline 1932 & 1.97 \\
\hline 1936 & 2.03 \\
\hline 1948 & 1.98 \\
\hline 1952 & 2.04 \\
\hline 1956 & 2.12 \\
\hline 1960 & 2.16 \\
\hline 1964 & 2.18 \\
\hline 1968 & 2.24 \\
\hline 1972 & 2.23 \\
\hline 1976 & 2.25 \\
\hline 1980 & 2.36 \\
\hline 1984 & 2.35 \\
\hline 1988 & 2.38 \\
\hline 1992 & 2.34 \\
\hline 1996 & 2.39 \\
\hline 2000 & 2.35 \\
\hline 2004 & 2.36 \\
\hline 2008 & 2.36 \\
\hline 2012 & 2.33 \\
\hline 2016 & 2.38 \\
\hline 2020 & 2.37 \\
\hline
\end{array}

  1. For the data in Table 1, determine:
  2.  i. the maximum \(\textit{Mgold}\) in metres   (1 mark)

  3. ii. the percentage of \(\textit{Mgold}\) values greater than 2.25 m.   (1 mark)

  4. The mean of these \(\textit{Mgold}\) values is 2.23 m, and the standard deviation is 0.15 m.
  5. Calculate the standardised \(z\)-score for the 2000 \(\textit{Mgold}\) of 2.35 m.   (1 mark)

  6. Construct a boxplot for the \(\textit{Mgold}\) data in Table 1 on the grid below.   (2 marks)

     

  1. A least squares line can also be used to model the association between \(\textit{Mgold}\) and \(\textit{year}\).
  2. Using the data from Table 1, determine the equation of the least squares line for this data set.
  3. Use the template below to write your answer.
  4. Round the values of the intercept and slope to three significant figures.   (2 marks)

     

  1. The coefficient of determination is 0.857
  2. Interpret the coefficient of determination in terms of \(\textit{Mgold}\) and \(\textit{year}\).   (1 mark)

Show Answers Only

a.i.   \(2.39\)

a.ii.  \(50\%\)

b.    \(0.8\)

c.     

d.   
    

e.    \(\text{A coefficient of determination of 85.7% shows the variation in}\)

\(\text{the}\ Mgold\ \text{that is explained by the variation in the }year.\)

Show Worked Solution

a.i.   \(2.39\)

a.ii.  \(\dfrac{11}{22}=50\%\)

b.     \(z\) \(=\dfrac{x-\overline x}{s_x}\)
    \(=\dfrac{2.35-2.23}{0.15}\)
    \(=0.8\)

  
c.    \(Q_2=\dfrac{2.33+2.25}{2}=2.29\)

\(Q_1=2.12, \ Q_3=2.36\)

\(\text{Min}\ =1.94, \ \text{Max}\ =2.39\)
  

d.   \(\text{Using CAS:}\)


  
 

Mean mark (d) 52%.
Mean mark (e) 52%.

e.    \(\text{A coefficient of determination of 85.7% shows the variation in}\)

\(\text{the}\ Mgold\ \text{that is explained by the variation in the }year.\)

BIOLOGY, M8 2024 HSC 11 MC

The data shows the proportion of adults living in Australia who are obese.
 

Which of the following can be observed from the data?

  1. The proportion of obese adults always increases with age.
  2. There is a greater percentage of men who are obese than women in all age groups.
  3. The proportion of women who are obese increases from 13% at 18–24 to 38% at 65–74.
  4. The proportion of men who are obese increases from 18% at 18–24 to 35% at 45–54, then decreases to 23% at age 85 and over.
Show Answers Only

\(C\)

Show Worked Solution
  • Options \(A, B\) and \(D\) can be shown to be incorrect with reference to the table.

\(\Rightarrow C\)

BIOLOGY, M8 2024 HSC 7 MC

How do stomata maintain water balance in plants?

  1. They close in hot weather to decrease transpiration.
  2. They open in cold weather to decrease transpiration.
  3. They open in hot weather to decrease evaporative cooling.
  4. They close in cold weather to decrease evaporative cooling.
Show Answers Only

\(A\)

Show Worked Solution
  • Stomata close in hot weather to decrease transpiration.
  • This adaptive response helps prevent excessive water loss during high temperatures and maintain proper water balance.

\(\Rightarrow A\)

BIOLOGY, M5 2024 HSC 4 MC

Which row of the table correctly identifies components of DNA?

\begin{align*}
\begin{array}{l}
\rule{0pt}{2.5ex} \ \rule[-1ex]{0pt}{0pt}& \\
\rule{0pt}{2.5ex}\textbf{A.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{B.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{C.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{D.}\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|c|c|}
\hline
\rule{0pt}{2.5ex}\textit{Phosphate} \rule[-1ex]{0pt}{0pt}& \quad \textit{Ribose} \quad & \textit{Deoxyribose} & \quad \textit{Uracil} \quad & \ \ \textit{Thymine}\ \ \\
\hline
\rule{0pt}{2.5ex}\checkmark \rule[-1ex]{0pt}{0pt}& \text{} & \checkmark & \checkmark & \text{} \\
\hline
\rule{0pt}{2.5ex}\text{} \rule[-1ex]{0pt}{0pt}& \checkmark & \text{} & \checkmark & \checkmark \\
\hline
\rule{0pt}{2.5ex}\text{} \rule[-1ex]{0pt}{0pt}& \checkmark & \checkmark & \text{} & \checkmark \\
\hline
\rule{0pt}{2.5ex}\checkmark \rule[-1ex]{0pt}{0pt}& \text{} & \checkmark & \text{} & \checkmark \\
\hline
\end{array}
\end{align*}

Show Answers Only

\(D\)

Show Worked Solution
  • DNA contains phosphate groups, deoxyribose sugar (not ribose), and thymine (not uracil which is found in RNA instead).
  • The last row with checkmarks for phosphate, deoxyribose, and thymine is therefore the only correct combination.

\(\Rightarrow D\)

BIOLOGY, M6 2024 HSC 3 MC

The image shows a chromosome that has undergone mutation. Each letter represents a gene.
 

What type of mutation has occurred?

  1. Deletion
  2. Duplication
  3. Inversion
  4. Substitution
Show Answers Only

\(B\)

Show Worked Solution
  • Looking at the sequence, we can see that genes C and E appear twice in the mutated chromosome (creating a repeat of genetic material).
  • This is characteristic of a duplication mutation rather than deletion (loss), inversion (reversal), or substitution (replacement).

\(\Rightarrow B\)

BIOLOGY, M6 2024 HSC 2 MC

Resin produced by spinifex grass has long been used by Aboriginal Peoples. Spinifex resin is currently used to produce medicinal creams.

What is this an example of?

  1. Biotechnology
  2. Selective breeding
  3. Artificial insemination
  4. Genetically modified organisms
Show Answers Only

\(A\)

Show Worked Solution
  • This is an example of biotechnology because it involves using traditional knowledge to harness a biological resource (spinifex resin) for medicinal purposes.
  • This fits the broad definition of biotechnology as using biological systems or processes to create useful products.

\(\Rightarrow A\)

CHEMISTRY, M6 2024 HSC 3 MC

Which of the following compounds can be correctly described as an Arrhenius base when dissolved in water?

  1. Sodium nitrate
  2. Sodium sulfate
  3. Sodium chloride
  4. Sodium hydroxide
Show Answers Only

\(D\)

Show Worked Solution
  • An Arrhenius base is a compound that increases the concentration of \(\ce{OH-}\) ions when it is dissolved in water.
  • Sodium hydroxide is the only compound that dissolves in water to produce hydroxide ions.
  •    \(\ce{NaOH(s) -> Na+(aq) + OH-(aq)}\)

\(\Rightarrow D\)

CHEMISTRY, M5 2024 HSC 2 MC

Aboriginal and Torres Strait Islander Peoples have used leaching in flowing water over several days to prepare various foods from plants that can be toxic to humans.

What was the reason for this?

  1. To react with toxins
  2. To dissolve low solubility toxins
  3. To prevent the food from decomposing
  4. To break down compounds that are difficult to digest
Show Answers Only

\(B\)

Show Worked Solution
  • The toxins form a equilibrium system: \(\ce{toxins(s)\rightleftharpoons toxins(aq)}\)
  • As the water flows away, the concentration of aqueous toxins decreases which shifts the equilibrium system to the right, causing more low solubility toxins to break down.

\(\Rightarrow B\)

Networks, GEN1 2024 VCAA 36 MC

Eight houses in an estate are to be connected to the internet via underground cables.

The network below shows the possible connections between the houses.

The vertices represent the houses.

The numbers on the edges represent the length of cable connecting pairs of houses, in metres.
 

 

The graph that represents the minimum length of cable needed to connect all the houses is
 


 

Show Answers Only

\(D\)

Show Worked Solution

\(\text{Consider all options}\)

\(\text{Option A: contains a circuit}\ \rightarrow\ \text{Eliminate A}\)

\(\text{Option B:}\ 19+18+16+15+16+14+18=116\)

\(\text{Option C:}\ 20+19+18+16+15+16+14=118\)

\(\text{Option D:}\ 19+18+16+15+16+14+17=115\)

\(\Rightarrow D\)

Networks, GEN1 2024 VCAA 34 MC

Consider the following graph.
 

A Eulerian trail through this graph could be

  1. \(\text{ABCDEF}\)
  2. \(\text{ACBDCFDEF}\)
  3. \(\text{BACBDCFDEF}\)
  4. \(\text{BDCABCDFCDEF}\)
Show Answers Only

\(C\)

Show Worked Solution

\(\text{An Eulerian trail has exactly 2 vertices of odd degree.}\)

\(\text{You must start on one and finish on the other ie B to F.}\)

\(\rightarrow\ \text{Eliminate A and B}\)

\(\text{A path cannot use the same edge twice}\ \rightarrow\ \text{Eliminate D}\)

\(\Rightarrow C\)

CHEMISTRY, M7 2024 HSC 1 MC

Which two substances are members of the same homologous series?
 

Show Answers Only

\(A\)

Show Worked Solution
  • A homologous series refers to compounds with the same or similar functional group and same general formula.
  • Both substances in \(A\) contain a hydroxyl group.

\(\Rightarrow A\)

Matrices, GEN1 2024 VCAA 28 MC

A primary school is hosting a sports day.

Students represent one of four teams: blue \((B)\), green \((G)\), red \((R)\) or yellow \((Y)\).

Students compete in one of three sports: football \((F)\), netball \((N)\) or tennis \((T)\).

Matrix \(W\) shows the number of students competing in each sport and the team they represent.

\begin{aligned} \\
& \quad B  \quad \ G \quad \  R \quad \ Y \\
W = & \begin{bmatrix}
85 & 60 & 64 & 71 \\
62 & 74 & 80 & 64 \\
63 & 76 & 66 & 75
\end{bmatrix}\begin{array}{l}
F\\
N\\
T
\end{array}
\end{aligned}

Matrix \(W\) is multiplied by the matrix \(\begin{bmatrix}1 \\ 1 \\ 1 \\ 1\end{bmatrix}\) to produce matrix \(X\).

Element \(x_{31}\) indicates that

  1. 210 students represent the blue team.
  2. 210 students compete in netball.
  3. 280 students compete in tennis.
  4. 280 students compete in football.
Show Answers Only

\(C\)

Show Worked Solution

\begin{aligned} \\
X = & \begin{bmatrix}
280 \\
280 \\
280
\end{bmatrix}\begin{array}{l}
F\\
N\\
T
\end{array}
\end{aligned}

\(\Rightarrow C\)

Matrices, GEN1 2024 VCAA 26 MC

A market stall sells three types of candles.

The cost of each type of candle is shown in matrix \(C\) below.

\begin{align}
C=\left[\begin{array}{lll}
25 & 32 & 43
\end{array}\right] \end{align}

Towards the end of the day, the cost of each item is discounted by 15%.

Which one of the following expressions can be used to determine each discounted price?

  1. \(0.15C\)
  2. \(0.85C\)
  3. \(8.5C\)
  4. \(15C\)
Show Answers Only

\(B\)

Show Worked Solution

\(\text{Discounted price is 85}\%\ \text{of the original price.}\)

\(\therefore, 0.85 is the multiplier}\)

\(\Rightarrow B\)

Matrices, GEN1 2024 VCAA 25 MC

Matrix \(J\) is a \(2 \times 3\) matrix.

Matrix \(K\) is a \(3 \times 1\) matrix.

Matrix \(L\) is added to the product \(J K\).

The order of matrix \(L\) is

  1. \(1 \times 3\)
  2. \(2 \times 1\)
  3. \(2 \times 3\)
  4. \(3 \times 2\)
Show Answers Only

\(B\)

Show Worked Solution

\(J\ \text{is order}\ 2\times 3\ \text{and}\ K\ \text{is order}\ 3\times 1\)

\(JK\ \text{is order}\ 2\times 1\)

\(\text{For addition}\ L\ \text{must also be}\ 2\times 1\)

\(\Rightarrow B\)

Data Analysis, GEN1 2024 VCAA 7 MC

Fiona plays nine holes of golf each week, and records her score.

Her mean score for all rounds in 2024 is 55.7

In one round, when she recorded a score of 48, her standardised score was  \(z=-1.75\)

The standard deviation for score in 2024 is

  1. 1.1
  2. 2.3
  3. 4.4
  4. 6.95
Show Answers Only

\(C\)

Show Worked Solution
\(z\) \(=\dfrac{x-\overline{x}}{s_x}\)
\(-1.75\) \(=\dfrac{48-55.7}{s_x}\)
\(s_x\) \(=\dfrac{48-55.7}{-1.75}\)
  \(=4.4\)

  
\(\Rightarrow C\)

Data Analysis, GEN1 2024 VCAA 5 MC

The number of siblings of each member of a class of 24 students was recorded.

The results are displayed in the table below.

\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline
\rule{0pt}{2.5ex} \ \ 2\ \ \rule[-1ex]{0pt}{0pt} & \ \ 1 \ \ & \ \ 3 \ \ & \ \ 2 \ \ & \ \ 1 \ \ & \ \ 1 \ \ & \ \ 1 \ \ & \ \ 4 \ \ & \ \ 1 \ \ & \ \ 1 \ \ & \ \ 1 \ \ & \ \ 1 \ \ \\
\hline
\rule{0pt}{2.5ex} 1 \rule[-1ex]{0pt}{0pt} & 2 & 1 & 2 & 2 & 1 & 3 & 4 & 2 & 2 & 3 & 1 \\
\hline
\end{array}

A boxplot was constructed to display the spread of the data.

Which one of the following statements about this boxplot is correct?

  1. There are no outliers.
  2. The value of the interquartile range (IQR) is 1.5
  3. The value of the median is 1.5
  4. All of the five-number summary values are whole numbers.
Show Answers Only

\(C\)

Show Worked Solution

\(Q_1=1,\ Q_2=1.5,\ Q_3=2\rightarrow\ \ \text{eliminate D}\)

\(IQR=2-1=1\rightarrow\ \ \text{eliminate B}\)

\(Q_2=1.5 \longrightarrow \text{Median }=1.5 \ \rightarrow\ \text{C correct}\)

\(Q_3+1.5\times IQR=2+1.5\times 1 = 3.5 \ \rightarrow\ \ \text{eliminate A}\)

\(\Rightarrow C\)

Data Analysis, GEN1 2024 VCAA 2 MC

Freddie organised a function at work. He surveyed the staff about their preferences.

He asked them about their payment preference (cash or electronic payment) and their budget preference (less than $50 or more than $50).

The variables in this survey, payment preference and budget preference, are

  1. both categorical variables.
  2. both numerical variables.
  3. categorical and numerical variables, respectively.
  4. numerical and categorical variables, respectively.
Show Answers Only

\(A\)

Show Worked Solution

\(\text{Payment preference is categorical.}\)

\(\text{Budget preference contains numbers, however, it cannot be}\)

\(\text{quantified, therefore it is also categorical.}\)

\(\Rightarrow A\)

Complex Numbers, EXT2 N2 2024 HSC 7 MC

It is given that \(\abs{z-1+i}=2\).

What is the maximum possible value of \(\abs{z}\)?

  1. \(\sqrt{2}\)
  2. \(\sqrt{10}\)
  3. \(2+\sqrt{2}\)
  4. \(2-\sqrt{2}\)
Show Answers Only

\(C\)

Show Worked Solution

\(\abs{z-1+i}=2 \ \Rightarrow \ \text{circle centre} \ \ (1,-i), \ \ \text {radius}=2\)
 
 

\(OA=\sqrt{1^2+1^2}=\sqrt{2}\)

\(AB=2 \ \ \text{(radius)}\)

\(\therefore \abs{z}_{\text{max}}=2+\sqrt{2}\)

\(\Rightarrow C\)

Mechanics, EXT2 M1 2024 HSC 15c

A bar magnet is held vertically. An object that is repelled by the magnet is to be dropped from directly above the magnet and will maintain a vertical trajectory. Let \(x\) be the distance of the object above the magnet.
 

The object is subject to acceleration due to gravity, \(g\), and an acceleration due to the magnet \(\dfrac{27 g}{x^3}\), so that the total acceleration of the object is given by

 \(a=\dfrac{27 g}{x^3}-g\)

The object is released from rest at  \(x=6\).

  1. Show that  \(v^2=g\left(\dfrac{51}{4}-2 x-\dfrac{27}{x^2}\right)\).   (2 marks)

  2. Find where the object next comes to rest, giving your answer correct to 1 decimal place.  (2 marks)

Show Answers Only

 

Show Worked Solution

i.    \(a=\dfrac{27 g}{x^3}-g\)

\(\dfrac{d}{dx}(\frac{1}{2}v^{2})\) \(= \dfrac{27g}{x^3}-g\)  
\(\dfrac{1}{2} v^2\) \(=-\dfrac{27 g}{2 x^2}-g x+c\)  

 
\(\text{When}\ \ x=6, v=0:\)

\(0\) \(=-\dfrac{27g}{2 \times 6^2}-6g+c\)  
\(c\) \(=\dfrac{459 g}{72}=\dfrac{51 g}{8}\)  

 

  \(\dfrac{1}{2} v^2\) \(=-\dfrac{27 g}{2 x^2}-g x+\dfrac{51 g}{8}\)
  \(v^2\) \(=-\dfrac{27 g}{x^2}-2 g x+\dfrac{51g }{4}\)
    \(=g\left(\dfrac{51}{4}-2 x-\dfrac{27}{x^2}\right)\)

  

ii.    \(\text{Find \(x\) when  \(v=0\):}\)

\(\dfrac{51}{4}-2 x-\dfrac{27}{x^2}\) \(=0\)  
\(51 x^2-8 x^3-108\) \(=0\)  
\(8 x^3-51 x^2+108\) \(=0\)  

 
\(\text{Given  \(x=6\)  is a root:}\)

♦♦♦ Mean mark (ii) 24%.

\(8 x^3-51 x^2+108=(x-6)\left(8 x^2-3 x-18\right)\)

\(\text{Other roots:}\)

  \(x\) \(=\dfrac{3 \pm \sqrt{9-4 \cdot 8 \cdot 18}}{2 \times 8}\)
    \(=\dfrac{3 \pm \sqrt{585}}{16}\)
    \(=\dfrac{3+3 \sqrt{65}}{16} \quad(x>0)\)
    \(=1.7 \ \text{units (1 d.p.)}\)

 
\(\therefore \ \text{Object next comes to rest at  \(x=1.7\) units}\) 

Vectors, EXT2 V1 2024 HSC 14e

The diagram shows triangle \(O Q A\).

The point \(P\) lies on \(O A\) so that  \(O P: O A=3: 5\).

The point \(B\) lies on \(O Q\) so that  \(O B: O Q=1: 3\).

The point \(R\) is the intersection of \(A B\) and \(P Q\).

The point \(T\) is chosen on \(A Q\) so that \(O, R\) and \(T\) are collinear.
 

Let  \(\underset{\sim}{a}=\overrightarrow{O A}, \ \underset{\sim}{b}=\overrightarrow{O B}\)  and  \(\overrightarrow{P R}=k \overrightarrow{P Q}\)  where \(k\) is a real number.

  1. Show that  \(\overrightarrow{O R}=\dfrac{3}{5}(1-k) \underset{\sim}{a}+3 k \underset{\sim}{b}\).   (2 marks)

Writing  \(\overrightarrow{A R}=h \overrightarrow{A B}\), where \(h\) is a real number, it can be shown that  \(\overrightarrow{O R}=(1-h) \underset{\sim}{a}+h \underset{\sim}{b}\).  (Do NOT prove this.)

  1. Show that  \(k=\dfrac{1}{6}\).   (2 marks)

  2. Find \(\overrightarrow{O T}\) in terms of \(\underset{\sim}{a}\) and \(\underset{\sim}{b}\).   (2 marks)

Show Answers Only

i.    \(\underset{\sim}{a}=\overrightarrow{O A}, \ \underset{\sim}{b}=\overrightarrow{O B}, \ \overrightarrow{P R}=k \overrightarrow{P Q}\)

\(\overrightarrow{O P}: \overrightarrow{O A}=3: 5 \ \Rightarrow \ \overrightarrow{O P} = \dfrac{3}{5} \times \overrightarrow{O A} \)

\(\overrightarrow{O B}: \overrightarrow{O Q}=1: 3\ \Rightarrow \ \overrightarrow{O Q} = 3 \times \overrightarrow{OB} \)

\(\text {Show } \overrightarrow{O R}=\dfrac{3}{5}(1-k) \underset{\sim}{a}+3 k \underset{\sim}{b}\)

  \(\overrightarrow{O R}\) \(=\overrightarrow{O P}+k \overrightarrow{P Q}\)
    \(=\overrightarrow{O P}+k(\overrightarrow{O Q}-\overrightarrow{O P})\)
    \(=(1-k) \overrightarrow{O P}+k \overrightarrow{O Q}\)
    \(=\dfrac{3}{5}(1-k)\underset{\sim}{a}+3 k \underset{\sim}{b}\)

 

ii.    \(\overrightarrow{A R}=h \overrightarrow{A B}, \quad h \in \mathbb{R}\)

\(\overrightarrow{OR}=(1-h) \underset{\sim}{a}+h \underset{\sim}{b} \ \ \text{(given)}\)

\(\overrightarrow{O R}=\dfrac{3}{5}(1-k) \underset{\sim}{a}+3 k \underset{\sim}{b} \ \ \text{(part(i))}\)

\(\text{Vector }\underset{\sim}{a} \neq \lambda \underset{\sim}{b}\ (\lambda \in \mathbb{R})\ \Rightarrow \ \text{linearly independent and are basis vectors for } \overrightarrow{O R}\).

\(\text {Equating coefficients:}\)

   \(\dfrac{3}{5}(1-k)=1-h\ \ldots\ (1)\)

   \(h=3 k\ \ldots\ (2)\)

\(\text{Substituting (2) into (1)}\)

     \(\dfrac{3}{5}(1-k)\) \(=1-3 k\)
  \(3-3 k\) \(=5-15 k\)
  \(k\) \(=\dfrac{1}{6}\)

 
iii.    \(\overrightarrow{O T}=\dfrac{3}{4}(\underset{\sim}{a}+\underset{\sim}{b})\)

Show Worked Solution

i.    \(\underset{\sim}{a}=\overrightarrow{O A}, \ \underset{\sim}{b}=\overrightarrow{O B}, \ \overrightarrow{P R}=k \overrightarrow{P Q}\)

\(\overrightarrow{O P}: \overrightarrow{O A}=3: 5 \ \Rightarrow \ \overrightarrow{O P} = \dfrac{3}{5} \times \overrightarrow{O A} \)

\(\overrightarrow{O B}: \overrightarrow{O Q}=1: 3\ \Rightarrow \ \overrightarrow{O Q} = 3 \times \overrightarrow{OB} \)

\(\text {Show } \overrightarrow{O R}=\dfrac{3}{5}(1-k) \underset{\sim}{a}+3 k \underset{\sim}{b}\)

  \(\overrightarrow{O R}\) \(=\overrightarrow{O P}+k \overrightarrow{P Q}\)
    \(=\overrightarrow{O P}+k(\overrightarrow{O Q}-\overrightarrow{O P})\)
    \(=(1-k) \overrightarrow{O P}+k \overrightarrow{O Q}\)
    \(=\dfrac{3}{5}(1-k)\underset{\sim}{a}+3 k \underset{\sim}{b}\)

  

ii.    \(\overrightarrow{A R}=h \overrightarrow{A B}, \quad h \in \mathbb{R}\)

\(\overrightarrow{OR}=(1-h) \underset{\sim}{a}+h \underset{\sim}{b} \ \ \text{(given)}\)

\(\overrightarrow{O R}=\dfrac{3}{5}(1-k) \underset{\sim}{a}+3 k \underset{\sim}{b} \ \ \text{(part(i))}\)

\(\text{Vector }\underset{\sim}{a} \neq \lambda \underset{\sim}{b}\ (\lambda \in \mathbb{R})\ \Rightarrow \ \text{linearly independent and are basis vectors for } \overrightarrow{O R}\).

\(\text {Equating coefficients:}\)

   \(\dfrac{3}{5}(1-k)=1-h\ \ldots\ (1)\)

   \(h=3 k\ \ldots\ (2)\)

\(\text{Substituting (2) into (1)}\)

     \(\dfrac{3}{5}(1-k)\) \(=1-3 k\)
  \(3-3 k\) \(=5-15 k\)
  \(k\) \(=\dfrac{1}{6}\)

 

iii.    \(\overrightarrow{O T}=\lambda \overrightarrow{O R}\)

\(\text {Using parts (i) and (ii):}\)

\(\overrightarrow{O R}=\dfrac{3}{5}\left(1-\dfrac{1}{6}\right)\underset{\sim}{a}+3\left(\dfrac{1}{6}\right) \underset{\sim}{b}=\dfrac{1}{2}\left(\underset{\sim}{a}+\underset{\sim}{b}\right)\)

\(\overrightarrow{O T}=\dfrac{\lambda}{2}(\underset{\sim}{a}+\underset{\sim}{b})\)

♦ Mean mark (iii) 45%.
 

\(\text {Find } \lambda:\)

  \(\overrightarrow{O T}\) \(=\overrightarrow{O A}+\mu \overrightarrow{A Q}\)
  \(\dfrac{\lambda}{2}(\underset{\sim}{a}+\underset{\sim}{b})\) \(=\underset{\sim}{a}+\mu(3 \underset{\sim}{b}-\underset{\sim}{a}) \quad \Big(\text{noting}\ \overrightarrow{A Q}=\overrightarrow{O Q}-\overrightarrow{O A}=3 \underset{\sim}{b}-\underset{\sim}{a}\Big)\)
    \(=\underset{\sim}{a}(1-\mu)+3 \mu \underset{\sim}{b}\)

 
\(\text {Equating coefficients:}\)

\(\dfrac{\lambda}{2}=3 \mu \ \Rightarrow \ \mu=\dfrac{\lambda}{6}\)

  \(1-\dfrac{\lambda}{6}\) \(=\dfrac{\lambda}{2}\)
  \(6-\lambda\) \(=3 \lambda\)
  \(\lambda\) \(=\dfrac{3}{2}\)

 
\(\therefore \overrightarrow{O T}=\dfrac{3}{4}(\underset{\sim}{a}+\underset{\sim}{b})\)

ENGINEERING, TE 2024 HSC 4 MC

Which row of the table correctly identifies characteristics of analogue and digital communications?

\begin{align*}
\begin{array}{c}
\ & \\
\ & \\
\rule{0pt}{2.5ex}\textbf{A.}\\
\rule{0pt}{2.5ex}\textbf{}\\
\rule{0pt}{2.5ex}\textbf{B.}\\
\rule{0pt}{2.5ex}\textbf{}\\
\rule{0pt}{2.5ex}\textbf{C.}\\
\rule{0pt}{2.5ex}\textbf{}\\
\rule{0pt}{2.5ex}\textbf{D.}\\
\rule{0pt}{2.5ex}\textbf{}\\
\end{array}
\begin{array}{|l|l|}
\hline
\rule[-1ex]{0pt}{0pt} \quad \quad \quad \quad \quad Analogue  & \rule[-1ex]{0pt}{0pt} \quad \quad \quad \quad \quad Digital \\
\hline
\rule[-1ex]{0pt}{0pt} \text{Continuous (varying) signal} & \rule[-1ex]{0pt}{0pt} \text{Discrete (binary) signal} \\
\rule[-1ex]{0pt}{0pt} \text{Less susceptible to signal degradation} & \rule[-1ex]{0pt}{0pt} \text{More susceptible to signal degradation} \\
\hline
\rule[-1ex]{0pt}{0pt} \text{Continuous (varying) signal} & \rule[-1ex]{0pt}{0pt} \text{Discrete (binary) signal} \\
\rule[-1ex]{0pt}{0pt} \text{More susceptible to signal degradation} & \rule[-1ex]{0pt}{0pt} \text{Less susceptible to signal degradation} \\
\hline
\rule[-1ex]{0pt}{0pt} \text{Discrete (binary) signal} & \rule[-1ex]{0pt}{0pt} \text{Continuous (varying) signal} \\
\rule[-1ex]{0pt}{0pt} \text{Less susceptible to signal degradation} & \rule[-1ex]{0pt}{0pt} \text{More susceptible to signal degradation} \\
\hline
\rule[-1ex]{0pt}{0pt} \text{Discrete (binary) signal} & \rule[-1ex]{0pt}{0pt} \text{Continuous (varying) signal} \\
\rule[-1ex]{0pt}{0pt} \text{More susceptible to signal degradation} & \rule[-1ex]{0pt}{0pt} \text{Less susceptible to signal degradation} \\
\hline
\end{array}
\end{align*}

Show Answers Only

\(B\)

Show Worked Solution
  • Analog signals are continuous and more susceptible to degradation while digital signals are discrete (binary) and less susceptible to degradation since they can be regenerated and error-corrected during transmission.

\(\Rightarrow B\)

ENGINEERING, PPT 2024 HSC 3 MC

A simplified image of a bicycle chain drive is shown.
 

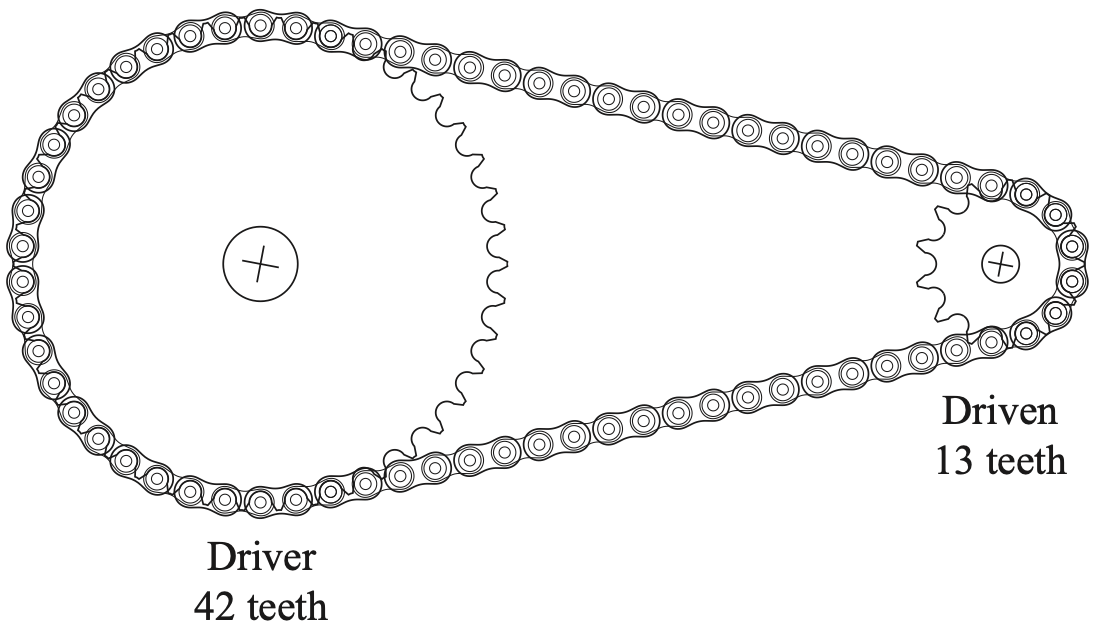
If a cyclist is pedalling at 70 revolutions per minute (RPM), what is the RPM of the driven wheel?

  1. 3.2
  2. 21.7
  3. 226.2
  4. 546.0
Show Answers Only

\(C\)

Show Worked Solution

\(\text{Velocity Ratio}\ (VR)\ = \dfrac{\text{output teeth}}{\text{input teeth}} = \dfrac{13}{42}=0.3095\)

\(\text{Output speed (RPM)}\ = \dfrac{\text{input speed}}{VR} = \dfrac{70}{0.3095}=226.2\)

\(\Rightarrow C\)

ENGINEERING, CS 2024 HSC 1 MC

A common house brick is shown.
 

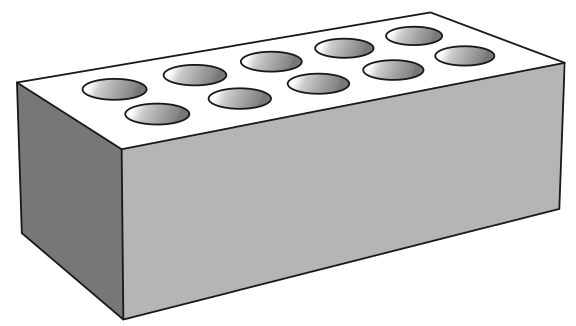
Which forming process was used to manufacture the brick?

  1. Forging
  2. Extrusion
  3. Slip casting
  4. Shell moulding
Show Answers Only

\(B\)

Show Worked Solution
  • Common house bricks are manufactured through extrusion, where clay is forced through a die to create a rectangular column that is then cut into individual brick lengths before drying and firing.

\(\Rightarrow B\)

Mechanics, EXT2 M1 2024 HSC 13c

A particle of unit mass moves horizontally in a straight line. It experiences a resistive force proportional to \(v^2\), where \(v\) m s\(^{-1}\) is the speed of the particle, so that the acceleration is given by  \(-k v^2\).

Initially the particle is at the origin and has a velocity of 40 m s\(^{-1}\) to the right. After the particle has moved 15 m to the right, its velocity is 10 m s\(^{-1}\) (to the right).

  1. Show that  \(v=40 e^{-k x}\).   (3 marks)

  2. Show that  \(k=\dfrac{\ln 4}{15}\).   (1 mark)

  3. At what time will the particle's velocity be 30 m s\(^{-1}\) to the right?   (3 marks)

Show Answers Only

i.    \(\ddot{x}=v \cdot \dfrac{d v}{d x}=-k v^2\)

  \(\dfrac{d v}{d x}\) \(=-k v\)
  \(\dfrac{d x}{d v}\) \(=-\dfrac{1}{k v}\)
  \(\displaystyle\int \frac{1}{v}\, d v\) \(=\displaystyle -\int k\, d x\)
  \(\ln \abs{v}\) \(=-k x+c\)
  \(v\) \(=e^{-k x+c}\)
    \(=A e^{-k x}\ \ (\text{where } A=e^c)\)

 
\(\text {When } x=0, v=40:\)

\(40=A e^{\circ} \ \Rightarrow \ A=40\)

\(\therefore V=40 \, e^{-k x}\)
 

ii.   \(\text {Show}\ \ k=\dfrac{\ln 4}{15}\)

\(\text {When } x=15, v=10:\)

  \(10\) \(=40 e^{-15 k}\)
  \(e^{-15 k}\) \(=\dfrac{1}{4}\)
  \(-15 k\) \(=\ln \left(\dfrac{1}{4}\right)\)
  \(15 k\) \(=\ln 4\)
  \(k\) \(=\dfrac{\ln 4}{15}\)

iii.  \(\dfrac{1}{8\,\ln 4}\  \text{seconds}\)

Show Worked Solution

i.    \(\ddot{x}=v \cdot \dfrac{d v}{d x}=-k v^2\)

  \(\dfrac{d v}{d x}\) \(=-k v\)
  \(\dfrac{d x}{d v}\) \(=-\dfrac{1}{k v}\)
  \(\displaystyle\int \frac{1}{v}\, d v\) \(=\displaystyle -\int k\, d x\)
  \(\ln \abs{v}\) \(=-k x+c\)
  \(v\) \(=e^{-k x+c}\)
    \(=A e^{-k x}\ \ (\text{where } A=e^c)\)

 
\(\text {When } x=0, v=40:\)

\(40=A e^{\circ} \ \Rightarrow \ A=40\)

\(\therefore V=40 \, e^{-k x}\)
 

ii.   \(\text {Show}\ \ k=\dfrac{\ln 4}{15}\)

\(\text {When } x=15, v=10:\)

  \(10\) \(=40 e^{-15 k}\)
  \(e^{-15 k}\) \(=\dfrac{1}{4}\)
  \(-15 k\) \(=\ln \left(\dfrac{1}{4}\right)\)
  \(15 k\) \(=\ln 4\)
  \(k\) \(=\dfrac{\ln 4}{15}\)

 

iii.   \(\text {Find}\ t\ \text {when}\ \ v=30:\)

  \(\dfrac{d v}{d t}\) \(=-k v^2\)
  \(\dfrac{d t}{d v}\) \(=-\dfrac{1}{k v^2}\)
  \(t\) \(=\displaystyle -\int \dfrac{1}{k v^2}\, d v=\dfrac{1}{k v}+c\)

 
\(\text {When}\ \ t=0, v=40:\)

\(0=\dfrac{1}{40 k}+c \ \Rightarrow \ c=-\dfrac{1}{40 k}\)
 

\(\text{Find \(t\) when  \(v=30\):}\)

  \(t\) \(=\dfrac{1}{30k}-\dfrac{1}{40k}\)
    \(=\dfrac{1}{120k}\)
    \(=\dfrac{15}{120\, \ln 4}\)
    \(=\dfrac{1}{8\,\ln 4}\  \text{seconds}\)

Vectors, EXT2 V1 2024 HSC 13a

The point \(A\) has position vector  \(8 \underset{\sim}{i}-6 \underset{\sim}{j}+5 \underset{\sim}{k}\). The line \(\ell\) has vector equation

\(x \underset{\sim}{i}+y \underset{\sim}{j}+z \underset{\sim}{k}=t(\underset{\sim}{i}+\underset{\sim}{j}+2 \underset{\sim}{k})\).

The point \(B\) lies on \(\ell\) and has position vector  \(p \underset{\sim}{i}+p \underset{\sim}{j}+2 p \underset{\sim}{k}\).

  1. Show that  \(\abs{A B}^2=6 p^2-24 p+125\).   (1 mark)

  2. Hence, or otherwise, determine the shortest distance between the point \(A\) and the line \(\ell\).  (2 marks)

Show Answers Only

i.     \(A\left(\begin{array}{c}8 \\ -6 \\ 5\end{array}\right), \quad \ell: \left(\begin{array}{l}x \\ y \\ z\end{array}\right)+t\left(\begin{array}{l}1 \\ 1 \\ 2\end{array}\right), \quad B\left(\begin{array}{c}p \\ p \\ 2 p\end{array}\right)\)
 

\(\overrightarrow{A B}=\left(\begin{array}{l}p \\ p \\ 2 p\end{array}\right)-\left(\begin{array}{c}8 \\ -6 \\ 5\end{array}\right)=\left(\begin{array}{c}p-8 \\ p+6 \\ 2 p-5\end{array}\right)\)
 

  \(\abs{AB}^2\) \(=(p-8)^2+(p+6)^2+(2 p-5)^2\)
    \(=p^2-16 p+64+p^2+12 p+36+4 p^2-20 p+25\)
    \(=6 p^2-24 p+125\)

 

ii.    \(\abs{AB}_{\text {min}}=\sqrt{101} \text { units}\)

Show Worked Solution

i.     \(A\left(\begin{array}{c}8 \\ -6 \\ 5\end{array}\right), \quad \ell: \left(\begin{array}{l}x \\ y \\ z\end{array}\right)+t\left(\begin{array}{l}1 \\ 1 \\ 2\end{array}\right), \quad B\left(\begin{array}{c}p \\ p \\ 2 p\end{array}\right)\)
 

\(\overrightarrow{A B}=\left(\begin{array}{l}p \\ p \\ 2 p\end{array}\right)-\left(\begin{array}{c}8 \\ -6 \\ 5\end{array}\right)=\left(\begin{array}{c}p-8 \\ p+6 \\ 2 p-5\end{array}\right)\)
 

  \(\abs{AB}^2\) \(=(p-8)^2+(p+6)^2+(2 p-5)^2\)
    \(=p^2-16 p+64+p^2+12 p+36+4 p^2-20 p+25\)
    \(=6 p^2-24 p+125\)

  

ii.    \(\text{Find shortest distance between \(A\) and \(\ell\).}\)

\(\Rightarrow \text { Find \(p\) when \(\abs{A B}\) is a minimum:}\)

\(\text{Minimum occurs when}\ \ p=\dfrac{-b}{2 a}=\dfrac{24}{2 \times 6}=2\)

\(\therefore \abs{AB}_{\text {min}}=\sqrt{6(2)^2-24(2)+125}=\sqrt{101} \text { units}\)

♦ Mean mark (ii) 45%.

Vectors, EXT2 V1 2024 HSC 12e

The line \(\ell\) passes through the points \(A(3,5,-4)\) and \(B(7,0,2)\).

  1. Find a vector equation of the line \(\ell\).   (1 mark)

  2. Determine, giving reasons, whether the point \(C(10,5,-2)\) lies on the line \(\ell\).   (2 marks)

Show Answers Only

i.    \(\text{ Equation of line:} \ \left(\begin{array}{c}3 \\ 5 \\ -4\end{array}\right)+\lambda\left(\begin{array}{c}4 \\ -5 \\ 6\end{array}\right),\ (\lambda \in \mathbb{R} )\)

ii.    \(\text{If \(C\) lies on the line}, \ \exists \lambda \in \mathbb{R}\  \ \text{such that:}\)

\(\left(\begin{array}{c}10 \\ 5 \\ -2\end{array}\right)=\left(\begin{array}{c}3 \\ -5 \\ 6\end{array}\right)+\lambda\left(\begin{array}{c}4 \\ -5 \\ 6\end{array}\right)\)

 
\(\text{Find \(\lambda\) for \(x\)-component: }\)

\(10=3+4 \lambda \ \Rightarrow \ \lambda=\dfrac{7}{4}\)

\(\text{Check \(\lambda=\dfrac{7}{4}\) for \(y\)-component:}\)

\(5=-5+\dfrac{7}{4}(-5) \ \ \Rightarrow\ \ \text{not correct}\)

\(\therefore C\  \text{does not lie on the line.}\)

Show Worked Solution

i.     \(A(3,5,-4), \quad B(7,0,2)\)

\(\overrightarrow{A B}=\left(\begin{array}{l}7 \\ 0 \\ 2\end{array}\right)-\left(\begin{array}{c}3 \\ 5 \\ -4\end{array}\right)=\left(\begin{array}{c}4 \\ -5 \\ 6\end{array}\right)\)

\(\therefore \text{ Equation of line:} \ \left(\begin{array}{c}3 \\ 5 \\ -4\end{array}\right)+\lambda\left(\begin{array}{c}4 \\ -5 \\ 6\end{array}\right),\ (\lambda \in \mathbb{R} )\)
 

ii.    \(\text{If \(C\) lies on the line}, \ \exists \lambda \in \mathbb{R}\  \ \text{such that:}\)

\(\left(\begin{array}{c}10 \\ 5 \\ -2\end{array}\right)=\left(\begin{array}{c}3 \\ -5 \\ 6\end{array}\right)+\lambda\left(\begin{array}{c}4 \\ -5 \\ 6\end{array}\right)\)

 
\(\text{Find \(\lambda\) for \(x\)-component: }\)

\(10=3+4 \lambda \ \Rightarrow \ \lambda=\dfrac{7}{4}\)

\(\text{Check \(\lambda=\dfrac{7}{4}\) for \(y\)-component:}\)

\(5=-5+\dfrac{7}{4}(-5) \ \ \Rightarrow\ \ \text{not correct}\)

\(\therefore C\  \text{does not lie on the line.}\)

Complex Numbers, EXT2 N1 2024 HSC 12c

Consider the equation  \(\abs{z}=z+8+12 i\), where  \(z=a+b i\)  is a complex number and \(a, b\) are real numbers.

  1. Explain why  \(b=-12\).   (1 mark)

  2. Hence, or otherwise, find \(z\).   (2 marks)

Show Answers Only

i.     \(\abs{z}=z+8+12i\)

\(z=a+b i\ \ \Rightarrow\ \ \abs{z}=\sqrt{a^2+b^2}\)

\(\text{Equating moduli:}\)

\(\sqrt{a^2+b^2}=a+b i+8+12 i=a+8+(b+12) i\)

\(\text{Since } \sqrt{a^2+b^2} \in \mathbb{R}:\)

\(b+12=0 \ \Rightarrow \ b=-12\)
 

ii.    \(z=5-12 i\)

Show Worked Solution

i.     \(\abs{z}=z+8+12i\)

\(z=a+b i\ \ \Rightarrow\ \ \abs{z}=\sqrt{a^2+b^2}\)

\(\text{Equating moduli:}\)

\(\sqrt{a^2+b^2}=a+b i+8+12 i=a+8+(b+12) i\)

\(\text{Since } \sqrt{a^2+b^2} \in \mathbb{R}:\)

\(b+12=0 \ \Rightarrow \ b=-12\)
  

ii.    \(\abs{a-12 i}\) \(=a+8\)
  \(\sqrt{a^2+144}\) \(=a+8\)
  \(a^2+144\) \(=a^2+16 a+64\)
  \(16a\) \(=80\)
  \(a\) \(=5\)
 
\(\therefore z=5-12 i\)

Calculus, EXT2 C1 2024 HSC 12b

Use partial fractions to find \(\displaystyle \int \frac{3 x^2+2 x+1}{(x-1)\left(x^2+1\right)}\, d x\)   (3 marks)

Show Answers Only

\(I=3 \ln \abs{x-1}+2 \tan ^{-1}(x)+c\)

Show Worked Solution

\(\displaystyle\int \dfrac{3 x^2+2 x+1}{(x-1)\left(x^2+1\right)}\, d x\)

\(\dfrac{3 x^2+2 x+1}{(x-1)\left(x^2+1\right)}=\dfrac{A}{(x-1)}+\dfrac{B x+C}{x^2+1}\)

  \(3 x^2+2 x+1\) \(=A\left(x^2+1\right)+(x-1)(B x+C)\)
    \(=A x^2+A+B x^2+C x-B x-C\)
    \(=(A+B) x^2+(C-B) x+A-C\)

 
\(\text {If } x=1:\)

\(3+2+1=2 A \ \Rightarrow \ A=3\)

\(A+B=3 \quad \quad \ \Rightarrow \ B=0\)

\(A-C=1 \quad \quad \ \Rightarrow \ C=2\)

  \(\therefore I\) \(=\displaystyle \int \frac{3}{x-1}+\frac{2}{x^2+1}\, d x\)
    \(=3 \ln \abs{x-1}+2 \tan ^{-1}(x)+c\)

Vectors, EXT2 V1 2024 HSC 12a

The vector \(\underset{\sim}{a}\) is \(\left(\begin{array}{l}1 \\ 2 \\ 3\end{array}\right)\) and the vector \(\underset{\sim}{b}\) is \(\left(\begin{array}{c}2 \\ 0 \\ -4\end{array}\right)\).

  1. Find \(\dfrac{\underset{\sim}{a} \cdot \underset{\sim}{b}}{\underset{\sim}{b} \cdot \underset{\sim}{b}}\, \underset{\sim}{b}\).   (1 mark)

  2. Show that  \(\underset{\sim}{a}-\dfrac{\underset{\sim}{a} \cdot \underset{\sim}{b}}{\underset{\sim}{b} \cdot \underset{\sim}{b}}\, \underset{\sim}{b}\)  is perpendicular to \(\underset{\sim}{b}\).  (2 marks)

Show Answers Only

1.     \(\left(\begin{array}{c}-1 \\ 0 \\ 2\end{array}\right)\)

ii.    \(\underset{\sim}{a}-\dfrac{\underset{\sim}{a} \cdot \underset{\sim}{b}}{\underset{\sim}{b} \cdot \underset{\sim}{b}}\, \underset{\sim}{b}=\left(\begin{array}{l}1 \\ 2 \\ 3\end{array}\right)-\left(\begin{array}{c}-1 \\ 0 \\ 2\end{array}\right)=\left(\begin{array}{l}2 \\ 2 \\ 1\end{array}\right)\)

\( \left(\underset{\sim}{a}-\dfrac{\underset{\sim}{a} \cdot \underset{\sim}{b}}{\underset{\sim}{b} \cdot \underset{\sim}{b}}\underset{\sim}{b}\right)\left(\begin{array}{c}-1 \\ 0 \\ 2\end{array}\right)=\left(\begin{array}{l}2 \\ 2 \\ 1\end{array}\right)\left(\begin{array}{c}-1 \\ 0 \\ 2\end{array}\right) = -2+0+2=0\)

\(\therefore\ \text {Vectors are perpendicular.}\)

Show Worked Solution

i.    \(\underset{\sim}{a}=\left(\begin{array}{l}1 \\ 2 \\ 3\end{array}\right), \quad \underset{\sim}{b}=\left(\begin{array}{c}2 \\ 0 \\ -4\end{array}\right)\)
 

\(\dfrac{\underset{\sim}{a} \cdot \underset{\sim}{b}}{\underset{\sim}{b} \cdot \underset{\sim}{b}}\, \underset{\sim}{b}=\dfrac{2+0-12}{4+0+16}\left(\begin{array}{c}2 \\ 0 \\ -4\end{array}\right)=-\dfrac{1}{2}\left(\begin{array}{c}2 \\ 0 \\ -4\end{array}\right)=\left(\begin{array}{c}-1 \\ 0 \\ 2\end{array}\right)\)

 
ii.    \(\underset{\sim}{a}-\dfrac{\underset{\sim}{a} \cdot \underset{\sim}{b}}{\underset{\sim}{b} \cdot \underset{\sim}{b}}\, \underset{\sim}{b}=\left(\begin{array}{l}1 \\ 2 \\ 3\end{array}\right)-\left(\begin{array}{c}-1 \\ 0 \\ 2\end{array}\right)=\left(\begin{array}{l}2 \\ 2 \\ 1\end{array}\right)\)
 

\( \left(\underset{\sim}{a}-\dfrac{\underset{\sim}{a} \cdot \underset{\sim}{b}}{\underset{\sim}{b} \cdot \underset{\sim}{b}}\,\underset{\sim}{b}\right)\left(\begin{array}{c}-1 \\ 0 \\ 2\end{array}\right)=\left(\begin{array}{l}2 \\ 2 \\ 1\end{array}\right)\left(\begin{array}{c}-1 \\ 0 \\ 2\end{array}\right) = -2+0+2=0\)

 
\(\therefore\ \text{Vectors are perpendicular.}\)

Complex Numbers, EXT2 N1 2024 HSC 11e

  1. Write the number  \(\sqrt{3}+i\)  in modulus-argument form.   (2 marks)

  2. Hence, or otherwise, write  \((\sqrt{3}+i)^7\)  in exact Cartesian form.   (2 marks)

Show Answers Only

i.     \(2 \text{cis}\left(\dfrac{\pi}{6}\right)=2\left(\cos \left(\dfrac{\pi}{6}\right)+i \sin \left(\dfrac{\pi}{6}\right)\right)\)

ii.    \(-64 \sqrt{3}-64 i\)

Show Worked Solution

i.     \(z=\sqrt{3}+i\)

\(|z|=\sqrt{3+1}=2\)

\(\arg (z)=\tan ^{-1}\left(\dfrac{1}{\sqrt{3}}\right)=\dfrac{\pi}{6}\)

\(z=2 \text{cis}\left(\dfrac{\pi}{6}\right)=2\left(\cos \left(\dfrac{\pi}{6}\right)+i \sin \left(\dfrac{\pi}{6}\right)\right)\)
 

ii.     \((\sqrt{3}+i)^7\) \(=2^7\left(\cos \left(\dfrac{7 \pi}{6}\right)+i \sin \left(\dfrac{7 \pi}{6}\right)\right)\)
    \(=128\left(-\dfrac{\sqrt{3}}{2}-\dfrac{1}{2} i\right)\)
    \(=-64 \sqrt{3}-64 i\)

Calculus, EXT2 C1 2024 HSC 11d

Evaluate  \(\displaystyle\int_0^{\frac{\pi}{2}} \dfrac{1}{\sin \theta+1}\, d \theta\).   (3 marks)

Show Answers Only

\(1\)

Show Worked Solution

\(t=\tan (\frac{\theta}{2}), \ \sin \theta=\dfrac{2 t}{1+t^2}\)

\(d t=\dfrac{1}{2} \sec ^2 (\frac{\theta}{2})\, d \theta \ \Rightarrow \ d \theta=\dfrac{2}{1+\tan ^2 (\frac{\theta}{2})}\, d t=\dfrac{2}{1+t^2}\, d t\)

\(\text {When}\ \ \theta=\dfrac{\pi}{2}\ \ \Rightarrow\ \ \tan (\frac{\theta}{2})=1\)

\(\text {When}\ \ \theta=0\ \ \Rightarrow\ \ \tan(\frac{\theta}{2})=0\)

\(\displaystyle{\int}_0^{\frac{\pi}{2}} \dfrac{1}{\sin \theta+1}\, d \theta\) \(=\displaystyle{\int}_0^1 \frac{1}{\dfrac{2 t}{1+t^2}+1} \cdot \frac{2}{1+t^2}\, d t\)
  \(=\displaystyle{\int}_0^1 \dfrac{2}{2 t+1+t^2}\, d t\)
  \(=\displaystyle{\int}_0^1 \dfrac{2}{(t+1)^2}\, d t\)
  \(=-\left[\dfrac{2}{t+1}\right]_0^1\)
  \(=-\left(\dfrac{2}{2}-2\right)\)
  \(=1\)

Vectors, EXT2 V1 2024 HSC 11c

Find the angle between the two vectors  \(\underset{\sim}{u}=\left(\begin{array}{c}1 \\ 2 \\ -2\end{array}\right)\) and  \(\underset{\sim}{v}=\left(\begin{array}{c}4 \\ -4 \\ 7\end{array}\right)\), giving your answer in radians, correct to 1 decimal place.   (2 marks)

Show Answers Only

\(\theta=2.3^c \ \ \text{(1 d.p.)}\)

Show Worked Solution

\(\underset{\sim}{u}=\left(\begin{array}{c}1 \\ 2 \\ -2\end{array}\right),\abs{\underset{\sim}{u}}=\sqrt{1+4+4}=3\)

\(\underset{\sim}{v}=\left(\begin{array}{c}4 \\ -4 \\ 7\end{array}\right),\abs{\underset{\sim}{v}}=\sqrt{16+16+49}=9\)

\(\cos \theta=\dfrac{\underset{\sim}{u} \cdot \underset{\sim}{v}}{|\underset{\sim}{u}||\underset{\sim}{v}|}=\dfrac{1 \times 4-2 \times 4-2 \times 7}{3 \times 9}=-\dfrac{2}{3}\)

\(\theta=\cos ^{-1}\left(-\dfrac{2}{3}\right)=2.30 \ldots=2.3^c \ \ \text{(1 d.p.)}\)

Calculus, EXT1 C3 2024 HSC 13a

In an experiment, the population of insects, \(P(t)\), was modelled by the logistic differential equation

\(\dfrac{d P}{d t}=P(2000-P)\)

where \(t\) is the time in days after the beginning of the experiment.

The diagram shows a direction field for this differential equation, with the point \(S\) representing the initial population.
 

  1. Explain why the graph of the solution that passes through the point \(S\) cannot also pass through the point \(T\).   (1 mark)

  2. Clearly sketch the graph of the solution that passes through the point \(S\).   (1 mark)

  3. Find the predicted value of the population, \(P(t)\), at which the rate of growth of the population is largest.   (2 marks)

Show Answers Only

 i.    \(\text{Any solution that passes through}\ S\ \text{will follow the}\)

\(\text{slope field (not crossing any lines) and approach a horizontal}\)

\(\text{asymptote at}\ P=2000\ \text{from the lower side}\ (P<2000).\)

ii.    
       

iii.  \(P= 1000\)

Show Worked Solution

 i.    \(\text{Any solution that passes through}\ S\ \text{will follow the}\)

\(\text{slope field (not crossing any lines) and approach a horizontal}\)

\(\text{asymptote at}\ P=2000\ \text{from the lower side}\ (P<2000).\)

ii.    
       

iii.  \(\dfrac{d P}{d t}=P(2000-P)\)

\(\text {Find \(P\) where  \(\dfrac{d P}{d t}\)  is a maximum.}\)

\(\text{Consider the graph}\ \ y=P(2000-P): \)

\(\Rightarrow \ \text {Graph is a concave down quadratic cutting at}\ \ P=0\ \ \text{and}\ \ P=2000\)

\(\Rightarrow \ \text{Max value of}\ \ P(2000-P)\ \ \Big(\text{i.e.}\ \dfrac{dP}{dt}\Big)\ \ \text{occurs at}\ \ P=1000\ \text{(axis).}\)

♦ Mean mark (iii) 51%.

Proof, EXT1 P1 2024 HSC 12d

Use mathematical induction to prove that  \(2^{3 n}+13\)  is divisible by 7 for all integers  \(n \geq 1\).   (3 marks)

Show Answers Only

\(\text{Proof (See worked solutions)}\)

Show Worked Solution

\(\text{Prove}\ \ 2^{3 n}+13\ \ \text{is divisible by 7 for}\ \ n \geq 1.\)

\(\text {If}\ \ n=1:\)

\(2^{3 \times 1}+13=21=3 \times 7\)

\(\therefore \text { True for } n=1.\)
 

\(\text {Assume true for } n=k:\)

\(2^{3 k}+13=7P \ \text{(where \(P\) is an integer)}\)

\(\Rightarrow 2^{3k}=7 P-13\ \ldots\ (1)\)

\(\text {Prove true for}\ \ n=k+1:\)

  \(2^{3(k+1)}+13\) \(=2^{3 k} \times 2^3+13\)
    \(=8\left(2^{3 k}\right)+13\)
    \(=8(7P-13)+13\ \ \text{(see (1) above)}\)
    \(=56 P-8 \times 13+13\)
    \(=7(8 P-13)\)

 
\(\Rightarrow \text { True for } n=k+1\)

\(\therefore\ \text{Since true for}\ \ n=1, \text{by PMI, true for integers}\ \ n \geqslant 1.\)

Calculus, EXT1 C3 2024 HSC 12b

The region, \(R\), is bounded by the function, \(y=x^3\), the \(x\)-axis and the lines  \(x=1\)  and  \(x=2\).

What is the volume of the solid of revolution obtained when the region \(R\) is rotated about the \(x\)-axis?   (3 marks)

Show Answers Only

\(V=\dfrac{127 \pi}{7} \ \ \text{u}^3\)

Show Worked Solution

  \(V\) \(=\pi \displaystyle \int_1^2 y^2\, d x\)
    \(=\pi \displaystyle \int_1^2 x^6\,d x\)
    \(=\pi\left[\dfrac{x^7}{7}\right]_1^2\)
    \(=\pi\left(\dfrac{2^7-1}{7}\right)\)
    \(=\dfrac{127 \pi}{7} \ \ \text{u}^3\)

Vectors, EXT1 V1 2024 HSC 12a

The vectors \(\displaystyle \binom{a^2}{2}\) and \(\displaystyle  \binom{a+5}{a-4}\) are perpendicular.

Find the possible values of \(a\).   (3 marks)

Show Answers Only

\(x=1,-4 \text { or }-2\)

Show Worked Solution

\(\text{If vectors are }\perp:\)

\(\displaystyle\binom{a^2}{2} \cdot\binom{a+5}{a-4}=0\)

\(a^3+5 a^2+2 a-8=0\)
 

\(\text{Test for roots:}\)

\(1^3+5 \times 1^2+2\times 1-8=0 \, \checkmark\)

\((a-1) \text{ is a factor.}\)

\(\text{By polynomial long division:}\)

\((a-1)\left(a^2+6 a+8\right)=0\)

\((a-1)(a+4)(a+2)=0\)

\(\therefore x=1,-4 \text { or }-2\)

Calculus, EXT1 C3 2024 HSC 11g

The region, \(R\), is bounded by the curves  \(y=\sin x, y=x\)  and the line  \(x=\dfrac{\pi}{2}\)  as shown in the diagram.
 

Find the area of the region \(R\).   (3 marks)

Show Answers Only

\(\dfrac{\pi^2}{8}-1\ \ \text{u}^2\)

Show Worked Solution

  \(R\) \(=\displaystyle{\int}_0^{\frac{\pi}{2}} x-\sin x \, d x\)
    \(=\left[\dfrac{x^2}{2}+\cos x\right]_0^{\frac{\pi}{2}}\)
    \(=\left[\left(\dfrac{\pi^2}{8}+\cos \dfrac{\pi}{2}\right)-(0+\cos 0)\right]\)
    \(=\dfrac{\pi^2}{8}-1\ \ \text{u}^2\)

Calculus, EXT1 C1 2024 HSC 11f

The volume of a sphere of radius \(r\) cm, is given by  \(V=\dfrac{4}{3} \pi r^3\),  and the volume of the sphere is increasing at a rate of \(10 \text{ cm}^3 \text{ s}^{-1}\).

Show that the rate of increase of the radius is given by  \(\dfrac{d r}{d t}=\dfrac{5}{2 \pi r^2} \text{ cm s}^{-1}\).   (2 marks)

Show Answers Only

  \(\dfrac{d r}{d t}\) \(=\dfrac{d V}{d t} \times \dfrac{d r}{d V}\)
    \(=10 \times \dfrac{1}{4 \pi r^2}\)
    \(=\dfrac{5}{2 \pi r^2} \text{ cm/s}\)

Show Worked Solution

\(V=\dfrac{4}{3} \pi r^3 \ \Rightarrow \ \dfrac{d V}{d r}=4 \pi r^2\)

\(\dfrac{d V}{d t}=10\)

  \(\dfrac{d r}{d t}\) \(=\dfrac{d V}{d t} \times \dfrac{d r}{d V}\)
    \(=10 \times \dfrac{1}{4 \pi r^2}\)
    \(=\dfrac{5}{2 \pi r^2} \text{ cm/s}\)

Calculus, EXT1 C3 2024 HSC 11d

Solve the differential equation  \(\dfrac{d y}{d x}=x y\),  given  \(y>0\). Express your answer in the form  \(y=e^{f(x)}\).   (2 marks)

Show Answers Only

\(y=e^{\frac{x^2}{2}}\)

Show Worked Solution

  \(\dfrac{d y}{d x}\) \(=x y\)
  \(\displaystyle\int \frac{1}{y}\, d y\) \(=\displaystyle\int x\, d x\)
  \(\ln y\) \(=\dfrac{1}{2} x^2+c\)
  \(y\) \(=e^{\frac{x^2}{2}+c}\)
    \(=e^{\frac{x^2}{2}} \cdot e^c\)
    \(=A e^{\frac{x^2}{2}} \text{ (where \(A=e^c)\)}\)

 
\(\therefore y=e^{\frac{x^2}{2}}\ \  \text{is a solution } (A=1)\)

Calculus, EXT1 C2 2024 HSC 11c

Using the substitution  \(u=x-1\), find  \(\displaystyle \int x \sqrt{x-1}\, d x\).   (3 marks)

Show Answers Only

\(\dfrac{2}{5}(x-1)^{\frac{5}{2}}+\dfrac{2}{3}(x-1)^{\frac{3}{2}}+c\)

Show Worked Solution

\(\displaystyle \int x \sqrt{x-1}\, d x \)

     
  \(u=x-1\) \(\Rightarrow \ x=u+1 \)
  \(\dfrac{d u}{d x}=1\)    \(\Rightarrow \ d u=d x\)

 

  \(\displaystyle\int(u+1) \sqrt{u+1-1}\, d u\) \(=\displaystyle{\int}(u+1) \sqrt{u} \, d u\)
    \(=\displaystyle{\int} u^{\frac{3}{2}}+u^{\frac{1}{2}}\, d u\)
    \(=\dfrac{2}{5} u^{\frac{5}{2}}+\dfrac{2}{3} u^{\frac{3}{2}}+c\)
    \(=\dfrac{2}{5}(x-1)^{\frac{5}{2}}+\dfrac{2}{3}(x-1)^{\frac{3}{2}}+c\)

Vectors, EXT1 V1 2024 HSC 11a

Consider the vectors  \(\underset{\sim}{a}=3 \underset{\sim}{i}+2 \underset{\sim}{j}\)  and  \(\underset{\sim}{b}=-\underset{\sim}{i}+4 \underset{\sim}{j}\).

  1. Find  \(2 \underset{\sim}{a}-\underset{\sim}{b}\).   (1 mark)

  2. Find  \(\underset{\sim}{a} \cdot \underset{\sim}{b}\).   (1 mark)

Show Answers Only

i.    \(\displaystyle \binom{7}{0}\)

ii.   \(5\)

Show Worked Solution

i.     \(\underset{\sim}{a}=3 \underset{\sim}{i}+2 \underset{\sim}{j}, \ \underset{\sim}{b}=-\underset{\sim}{i}+4 \underset{\sim}{j}\)

\(2 \underset{\sim}{a}-\underset{\sim}{b}=2 \displaystyle \binom{3}{2}-\binom{-1}{4}=\binom{6}{4}-\binom{-1}{4}=\binom{7}{0}\)
 

ii.    \(\underset{\sim}{a} \cdot \underset{\sim}{b}=\displaystyle\binom{3}{2}\binom{-1}{4}=3 \times(-1)+2 \times 4=5\).

CHEMISTRY, M2 EQ-Bank 2 MC

Which is the correct balanced formula equation for the reaction of potassium with water?

  1. \(\ce{K(s) + H2O(l) -> KOH(aq) + H2(g)}\)
  2. \(\ce{2K(s) + 2H2O(aq) -> 2KOH(aq) + H2(g)}\)
  3. \(\ce{2K(s) + 2H2O(l) -> 2KOH(aq) + H2(g)}\)
  4. \(\ce{K(s) + 2H2O(aq) -> KOH(aq) + 2H2(g)}\)
Show Answers Only

\(C\)

Show Worked Solution
  • The correct chemical equation is:
  •    \(\ce{2K(s) + 2H2O(l) -> 2KOH(aq) + H2(g)}\) 
  • The state of water is always liquid. An aqueous solution refers to a solution where a substance has been dissolved into water.

\(\Rightarrow C\)

CHEMISTRY, M2 EQ-Bank 2

In an experiment, calcium carbonate \(\ce{(CaCO3)}\) is heated strongly to produce calcium oxide \(\ce{(CaO)}\) and carbon dioxide according to the reaction below:

\(\ce{CaCO3(s) -> CaO(s) + CO2(g)}\)

A student starts with 50.0 g of calcium carbonate. After heating, they collect 28.0 g of calcium oxide.

  1. Using the law of conservation of mass, calculate the mass of carbon dioxide gas produced in this reaction.   (2 marks)
  1. Explain how the law of conservation of mass applies to this reaction.   (2 marks)
Show Answers Only

a.    \(22.0\ \text{g}\)

b.    Application of law to reaction:

  • The mass of reactants in a chemical reaction must equal the mass of the products.
  • Here, the 50.0 g of calcium carbonate decomposes into 28.0 g of calcium oxide and 22.0 g of carbon dioxide gas.
  • The total mass of products (28.0 g + 22.0 g) equals the initial mass of reactants (50.0 g), confirming that mass is conserved in this reaction.
Show Worked Solution

a.    Law of conservation of mass:

  • The total mass of reactants must equal the total mass of products.
  •   \(m\ce{(CO2)}=m\ce{(CaCO3)}-m\ce{(CaO)}= 50.0-28.0=22.0\ \text{g}\)

b.    Application of law to reaction:

  • The mass of reactants in a chemical reaction must equal the mass of the products.
  • Here, the 50.0 g of calcium carbonate decomposes into 28.0 g of calcium oxide and 22.0 g of carbon dioxide gas.
  • The total mass of products (28.0 g + 22.0 g) equals the initial mass of reactants (50.0 g), confirming that mass is conserved in this reaction.