SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

CORE, FUR2 SM-Bank 1

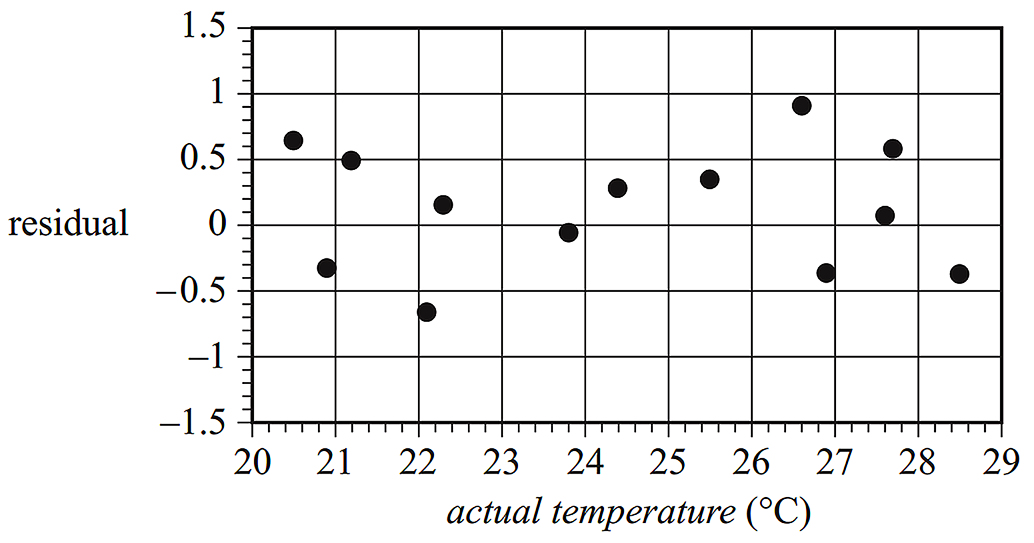
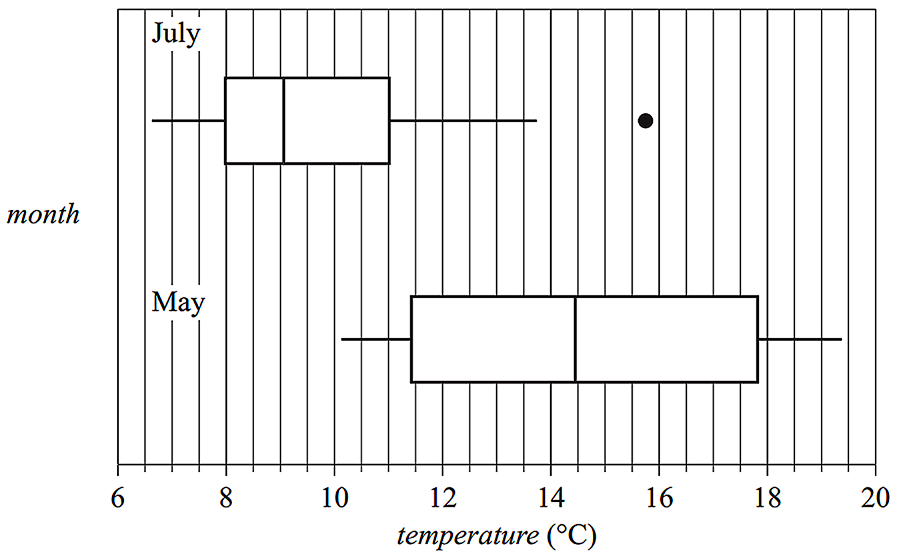
Joe buys a tractor under a buy-back scheme. This scheme gives Joe the right to sell the tractor back to the dealer through either a flat rate depreciation or unit cost depreciation.

  1. The recurrence relation below can be used to calculate the price Joe sells the tractor back to the dealer `(P_n)`, based on the flat rate depreciation, after `n` years
     
    `qquadP_0 = 56\ 000,qquadP_n = P_(n-1)-7000`
     

    1. Write the general rule to find the value of `P_n` in terms of `n`.?   (1 mark)
    2. Hence or otherwise, find the time it will take Joe's tractor to lose half of its value.   (1 mark)
  2. Joe uses the unit cost method to depreciate his tractor, he depreciates $2.75 per kilometre travelled.
    1. How many kilometres does Joe's tractor need to travel for half its value to be depreciated? Round your answer to the nearest kilometre?   (1 mark)
    2. Joe's tractor travels, on average, 2500 kilometres per year. Which method, flat rate depreciation or unit cost depreciation, will result in the greater annual depreciation? Write down the greater depreciation amount correct to the nearest dollar.   (1 mark)

Show Answers Only

  1. i.  `P_n = 56\ 000-7000n`
    ii. `4\ text(years)`
  2. i. `10\ 182\ text{km  (nearest km)}`
    ii. `text(The flat rate depreciation results in an extra)`
         `text($125 depreciation each year.)`

Show Worked Solution

a.i.    `P_1` `= P_0-7000`
  `P_2` `= P_0-7000-7000`
    `= 56\ 000-7000 xx 2`
  `vdots`  
  `P_n`  `= 56\ 000-7000n` 

 

a.ii.    `text(Depreciated value)` `= 56\ 000 ÷ 2=$28\ 000`

`text(Find)\ n,`

`28\ 000` `= 56\ 000-7000n`
`7000n` `= 28\ 000`
`:. n` `= 4\ text(years)`

 

b.i.    `text(Distance travelled)` `= ((56\ 000-28\ 000))/2.75`
    `= 10\ 181.81…`
    `= 10\ 182\ text{km  (nearest km)}`

  
b.ii.   `text(Annual depreciation of unit cost)`

`= 2500 xx $2.75`

`= $6875`

`text(Annual flat rate depreciation = $7000)`

`text(Difference)\ = 7000-6875 = $125`
 

`:.\ text(The flat rate depreciation results in an extra)`

 `text($125 depreciation each year.)`

NETWORKS, FUR2 2016 VCAA 2

The suburb of Alooma has a skateboard park with seven ramps.

The ramps are shown as vertices `T`, `U`, `V`, `W`, `X`, `Y` and `Z` on the graph below.
 

 

The tracks between ramps `U` and `V` and between ramps `W` and `X` are rough, as shown on the graph above.

  1. Nathan begins skating at ramp `W` and follows an Eulerian trail.

     

    At which ramp does Nathan finish?   (1 mark)

  2. Zoe begins skating at ramp `X` and follows a Hamiltonian path.

     

    The path she chooses does not include the two rough tracks.

     

    Write down a path that Zoe could take from start to finish.   (1 mark)

  3. Birra can skate over any of the tracks, including the rough tracks.

     

    He begins skating at ramp `X` and will complete a Hamiltonian cycle.

     

    In how many ways could he do this?   (1 mark) 

Show Answers Only
  1. `U`
  2. `XYTUZVW`
    `XYTUZWV`
  3. `4\ text(ways)`
Show Worked Solution

a.   `text{The Eulerian trail (visits each edge exactly once):}`

“XYZWVZUYTU`

`:. text(Finishes at ramp)\ U.`
  

b.   `text{Hamiltonian Paths (touch each vertex exactly once):}`

`XYTUZVW`

`XYTUZWV`
  

c.   `text(Hamiltonian cycles:)`

♦♦ Mean mark 31%.

`XYTUZVWX`

`XYTUVZWX`

`text(These two cycles can be reversed)`

`text(to add two more possibilities.)`

`XWVZUTYX`

`XWZVUTYX`

`:. 4\ text(ways.)`

GRAPHS, FUR2 2016 VCAA 2

The bonus money is provided by a company that manufactures and sells hockey balls.

The cost, in dollars, of manufacturing a certain number of balls can be found using the equation

cost = 1200 + 1.5 × number of balls

  1. How many balls would be manufactured if the cost is $1650?  (1 mark)
  2. On the grid below, sketch the graph of the relationship between the manufacturing cost and the number of balls manufactured.  (1 mark)

     

  3. The company will break even on the sale of hockey balls when it manufactures and sells 200 hockey balls.

     

    Find the selling price of one hockey ball.  (1 mark) 

Show Answers Only
  1. `300`

  3. `$7.50\ text(per ball)`
Show Worked Solution
a.    `1200 + 1.5 xx n` `= 1650`
  `:. n` `= ((1650 – 1200))/1.5`
    `= 300`

 

b.   

 

c.   `text(When)\ n = 200,`

`C` `= 1200 + 1.5 xx 200`
  `= 1500`

 

`:.\ text(Selling price if break even)`

`= 1500/200`

`= $7.50\ text(per ball)`

GRAPHS, FUR2 2016 VCAA 1

Maria is a hockey player. She is paid a bonus that depends on the number of goals that she scores in a season.

The graph below shows the value of Maria’s bonus against the number of goals that she scores in a season.

  1. What is the value of Maria’s bonus if she scores seven goals in a season?  (1 mark) 
  2. What is the least number of goals that Maria must score in a season to receive a bonus of $2500?  (1 mark)

Another player, Bianca, is paid a bonus of $125 for every goal that she scores in a season.

  1. What is the value of Bianca’s bonus if she scores eight goals in a season?  (1 mark)
  2. At the end of the season, both players have scored the same number of goals and receive the same bonus amount.

     

    How many goals did Maria and Bianca each score in the season?  (1 mark)

Show Answers Only
  1. `$1500`
  2. `15`
  3. `$1000`
  4. `text(28 goals)`
Show Worked Solution

a.   `$1500`

 

b.   `15`

 

c.    `text(Bonus)` `= 8 xx 125`
    `= $1000`

 

d.   `text(Draw the graph of Bianca’s payments on)`

`text(the same graph.)`

`text(The intersection is where both players)`

`text(receive the same bonus amount.)`

`:.\ text(Maria and Bianca each score 28 goals.)`

MATRICES, FUR2 2016 VCAA 2

A travel company has five employees, Amara (`A`), Ben (`B`), Cheng (`C`), Dana (`D`) and Elka (`E`).

The company allows each employee to send a direct message to another employee only as shown in the communication matrix `G` below.

The matrix `G^2` is also shown below.
 

`{:(),(),(G = text(sender )):}{:(qquadqquadqquad\ text(receiver)),(qquadqquadAquadBquadCquadDquadE),({:(A),(B),(C),(D),(E):}[(0,1,1,1,1),(1,0,1,0,0),(1,1,0,1,0),(0,1,0,0,1),(0,0,0,1,0)]):}qquad{:(),(),(G^2 = text(sender )):}{:(qquadqquadqquad\ text(receiver)),(qquadqquadAquadBquadCquadDquadE),({:(A),(B),(C),(D),(E):}[(2,2,1,2,1),(1,2,1,2,1),(1,2,2,1,2),(1,0,1,1,0),(0,1,0,0,1)]):}`
 

The 1 in row `E`, column `D` of matrix `G` indicates that Elka (sender) can send a direct message to Dana (receiver).

The 0 in row `E`, column `C` of matrix `G` indicates that Elka cannot send a direct message to Cheng.

  1. To whom can Dana send a direct message?   (1 mark)

  2. Cheng needs to send a message to Elka, but cannot do this directly.
  3. Write down the names of the employees who can send the message from Cheng directly to Elka.   (1 mark) 

Show Answers Only
  1. `text(Ben and Elka)`
  2. `text(Amara and Dana)`
Show Worked Solution

a.   `text(Ben and Elka)`
 

b.   `text(Amara and Dana)`

MATRICES, FUR2 2016 VCAA 1

A travel company arranges flight (`F`), hotel (`H`), performance (`P`) and tour (`T`) bookings.

Matrix `C` contains the number of each type of booking for a month.

`C = [(85),(38),(24),(43)]{:(F),(H),(P),(T):}`

  1. Write down the order of matrix `C`.   (1 mark)

A booking fee, per person, is collected by the travel company for each type of booking.

Matrix `G` contains the booking fees, in dollars, per booking.

`{:((qquadqquadquadF,\ H,\ P,\ T)),(G = [(40,25,15,30)]):}`

  1.  i. Calculate the matrix product  `J = G × C`.   (1 mark)

  2. ii. What does matrix `J` represent?   (1 mark) 

Show Answers Only
  1. `4 xx 1`
    1. `[6000]`
    2. `J\ text(represents the total booking fees for the travel)`
      `text(company in the given month.)`
Show Worked Solution

a.   `text(Order:)\ 4 xx 1`
 

b.i.    `J = [(40,25,15,30)][(85),(38),(24),(43)]= [6000]`

 
b.ii.  `J\ text(represents the total booking fees for the)`

♦ Mean mark 42%.

 `text(travel company in the given month.)`

GEOMETRY, FUR2 2016 VCAA 2

Salena practises golf at a driving range by hitting golf balls from point  `T`.

The first ball that Salena hits travels directly north, landing at point  `A`.

The second ball that Salena hits travels 50 m on a bearing of 030°, landing at point  `B`.

The diagram below shows the positions of the two balls after they have landed.
  

  1. How far apart, in metres, are the two golf balls?  (1 mark)
  2. A fence is positioned at the end of the driving range.

     

    The fence is 16.8 m high and is 200 m from the point  `T`.


     
     
    What is the angle of elevation from  `T`  to the top of the fence?

     

    Round your answer to the nearest degree.  (1 mark) 

Show Answers Only
  1. `25\ text(m)`
  2. `5^@\ text{(nearest degree)}`
Show Worked Solution

a.   `text(Let)\ \ d\ text(= distance apart)`

`sin30^@` `= d/50`
`:. d` `= 50 xx sin 30^@`
  `= 25\ text(m)`

 

b.   `text(Let)\ \ x^@\ text(= angle of elevation from)\ T`

`tanx` `= 16.8/200`
  `= 0.084`
`:. x` `= 4.801…`
  `= 5^@\ text{(nearest degree)}`

GEOMETRY, FUR2 2016 VCAA 1

A golf ball is spherical in shape and has a radius of 21.4 mm, as shown in the diagram below.

Assume that the surface of the golf ball is smooth.

  1. What is the surface area of the golf ball shown?

     

    Round your answer to the nearest square millimetre.  (1 mark)

  2. Golf balls are sold in a rectangular box that contains five identical golf balls, as shown in the diagram below.

     


     

    What is the minimum length, in millimetres, of the box?  (1 mark)

Show Answers Only
  1. `5755\ text(mm²)`
  2. `214\ text(mm)`
Show Worked Solution
a.    `text(Surface Area)` `= 4pir^2`
    `= 4 xx pi xx 21.4^2`
    `= 5754.89…`
    `= 5755\ text(mm²)`

 

b.    `text(Minimum length)` `= 21.4 xx 10`
    `= 214\ text(mm)`

CORE, FUR2 2016 VCAA 5

Ken has opened a savings account to save money to buy a new caravan.

The amount of money in the savings account after `n` years, `V_n`, can be modelled by the recurrence relation shown below.

`V_0 = 15000, qquad qquad qquad V_(n + 1) = 1.04 xx V_n`

  1. How much money did Ken initially deposit into the savings account?  (1 mark)

  2. Use recursion to write down calculations that show that the amount of money in Ken’s savings account after two years, `V_2`, will be $16 224.  (1 mark)

  3. What is the annual percentage compound interest rate for this savings account?  (1 mark)

  4. The amount of money in the account after `n` years, `Vn` , can also be determined using a rule.
    i.     Complete the rule below by writing the appropriate numbers in the boxes provided.   (1 mark)

    `V_n =` 
     
    		 `­^n xx`
     
  5. ii. How much money will be in Ken’s savings account after 10 years?   (1 mark)

Show Answers Only
  1. `$15000`
  2. `text(Proof)\ text{(See Worked Solutions)}`
  3. `4 text(%)`
  4. i. `text(See Worked Solutions)`
    ii. `$22\ 203.66` 
Show Worked Solution
a.    `text(Initial deposit)` `= V_0`
    `= $15\ 000`
b.    `V_0` `= $15\ 000`
  `V_1` `= 1.04 xx 15\ 000`
    `= $15\ 600`
  `V_2` `= 1.04 xx 15\ 600`
    `= $16\ 224\ text(… as required.)`

MARKER’S COMMENT: (b) Stating `V_2 =1.04^2 xx 15\ 600` `=16\ 224` is not using recursion as required here and did not gain a mark.
c.    `text(Annual compound interest)` `= 0.04 xx 100`
    `= 4 text(%)`

 

d.i.   `V_n` `= 1.04^n xx V_0`
d.ii.    `V_10` `= 1.04^10 xx 15\ 000`
    `= $22\ 203.664…`
    `= $22\ 203.66\ text{(nearest cent)}`

♦ Mean mark (d)(ii) 47%.
MARKER’S COMMENT: Rounding to $22 203.70 lost a mark!

CORE, FUR2 2016 VCAA 3

The data in the table below shows a sample of actual temperatures and apparent temperatures recorded at a weather station. A scatterplot of the data is also shown.

The data will be used to investigate the association between the variables apparent temperature and actual temperature.
 

  1. Use the scatterplot to describe the association between apparent temperature and actual temperature in terms of strength, direction and form.   (1 mark)

  2.  i. Determine the equation of the least squares line that can be used to predict the apparent temperature from the actual temperature.
  3. Write the values of the intercept and slope of this least squares line in the appropriate boxes provided below.
  4. Round your answers to two significant figures.   (3 marks)
     apparent temperature `=`    
 
 `+`  
 
 `xx`   actual temperature
  1. ii. Interpret the intercept of the least squares line in terms of the variables apparent temperature and actual temperature.   (1 mark)

  2. The coefficient of determination for the association between the variables apparent temperature and actual temperature is 0.97
  3. Interpret the coefficient of determination in terms of these variables.   (1 mark)

  4. The residual plot obtained when the least squares line was fitted to the data is shown below.
     
     
  5.  i. A residual plot can be used to test an assumption about the nature of the association between two numerical variables.
  6.     What is this assumption?   (1 mark)
  7. ii. Does the residual plot above support this assumption? Explain your answer.   (1 mark)
Show Answers Only

a.   `text(Strong, positive and linear)`

b.i.  `text(apparent temperature) = -1.7 xx 0.94 xx text(actual temperature)`

b.ii.  `text(When actual temperature is 0°C, on average,)`

`text(the apparent temperature is)\ − 1.7^@\text(C.)`

c.  `text(97% of the variation in the apparent temperature can be explained)`

`text(by the variation in the actual temperature.)`

d.i.  `text(There is a linear relationship between the two variables.)`

d.ii.  `text(The random pattern supports the assumption.)`

`text{(Students should refer to randomness or a lack of pattern}`

`text{explicitly here).}`

Show Worked Solution

a.   `text(Strong, positive and linear)`
 

b.i.   `text(By calculator:)`

`text(apparent temperature) = -1.7 xx 0.94 xx text(actual temperature)`
 

♦♦ Mean mark of part (b)(ii) – 28%.
MARKER’S COMMENT: “the predicted apparent temp is -1.7°C” also gained a mark.
b.ii.    `text(When actual temperature is 0°C, on average,)`
 

`text(the apparent temperature is)\ − 1.7^@\text(C.)`

 

♦ Mean mark 49%.
IMPORTANT: Any mention of causality loses a mark!

c.  `text(97% of the variation in the apparent temperature can be explained)`

`text(by the variation in the actual temperature.)`
  

d.i.  `text(There is a linear relationship between the two variables.)`

♦ Mean mark of both parts of (d) was 46%.

d.ii.  `text(The random pattern supports the assumption.)`

`text{(Students should refer to randomness or a lack of pattern}`

`text{explicitly here).}`

CORE, FUR2 2016 VCAA 2

A weather station records daily maximum temperatures.

  1. The five-number summary for the distribution of maximum temperatures for the month of February is displayed in the table below.

 

  1. There are no outliers in this distribution.
  2.  i. Use the five-number summary above to construct a boxplot on the grid below.   (1 mark)

 

  1. ii. What percentage of days had a maximum temperature of 21°C, or greater, in this particular February?   (1 mark)

  2. The boxplots below display the distribution of maximum daily temperature for the months of May and July.
     

  3.   i. Describe the shapes of the distributions of daily temperature (including outliers) for July and for May.   (1 mark)

  4.  ii. Determine the value of the upper fence for the July boxplot.   (1 mark)

  5. iii. Using the information from the boxplots, explain why the maximum daily temperature is associated with the month of the year. Quote the values of appropriate statistics in your response.   (1 mark)

Show Answers Only
a.i.   

a.ii.   `text(75%)`

b.i.    `text(July – Positively skewed with an outlier.)`
  `text(May – Symmetrical with no outliers.)`

b.ii.  `15.5^@\text(C)`

b.iii. `text{The median temperature in May (14.5°C)}`

`text(differs from the median temperature in July)`

`text{(just over 9°C). This difference is why the}`

`text(maximum daily temperature is associated)`

`text(with the month.)`

Show Worked Solution
a.i.   

a.ii.   `text(75%)`

MARKER’S COMMENT: Incorrect May descriptors included “evenly or normally distributed”, “bell shaped” and “symmetrically skewed.”
b.i.    `text(July – Positively skewed with an outlier.)`
  `text(May – Symmetrical with no outliers.)`

 

b.ii.    `text(Upper fence)` `= Q_3 + 1.5 xx IQR`
    `= 11 + 1.5 xx (11 – 8)`
    `= 11 + 4.5`
    `= 15.5^@\text(C)`
♦♦ Mean mark (b)(iii) – 30%.
COMMENT: Refer to the difference in medians. Just quoting the numbers was not enough to gain a mark here.

b.iii. `text{The median temperature in May (14.5°C)}`

`text(differs from the median temperature in July)`

`text{(just over 9°C). This difference is why the}`

`text(maximum daily temperature is associated)`

`text(with the month.)`

CORE, FUR2 2016 VCAA 1

The dot plot below shows the distribution of daily rainfall, in millimetres, at a weather station for 30 days in September.
 

 

  1. Write down the
  2.  i. range   (1 mark)

  3. ii. median   (1 mark)

  1. Circle the data point on the dot plot above that corresponds to the third quartile `(Q_3).`   (1 mark)

  2. Write down the
  3.  i. the number of days on which no rainfall was recorded.   (1 mark)

  4. ii. the percentage of days on which the daily rainfall exceeded 12 mm.   (1 mark)

  1. Use the grid below to construct a histogram that displays the distribution of daily rainfall for the month of September. Use interval widths of two with the first interval starting at 0.   (2 marks) 

  

Show Answers Only
    1. `17.8\ text(mm)`
    2. `0`
  2. `text(See Worked Solutions)`

     

    1. `16\ text(days)`
    2. `10\text(%)`
  4. `text(See Worked Solutions)`
Show Worked Solution
a.i.    `text(Range)` `=\ text(High) – text(Low)`
    `= 17.8 – 0`
    `= 17.8\ text(mm)`
     

a.ii.   `text(30 data points)`

`text(Median)` `= text{15th + 16th}/2`
  `= 0`

 

b.   

 

c.i.   `16\ text(days)`

c.ii.    `text(Percentage)` `= 3/30 xx 100`
    `= 10\ text(%)`

 

d.   

GRAPHS, FUR1 2016 VCAA 3 MC

The graph below shows a straight line that passes through the points (6, 6) and (8, 9).

The coordinates of the point where the line crosses the `x`-axis are

  1. `(–3, 0)`
  2. `(1, 0)`
  3. `(1.5, 0)`
  4. `(2, 0)`
  5. `(4, 0)`
Show Answers Only

`D`

Show Worked Solution
`m` `= (y_2 – y_1)/(x_2 – x_1)`
  `= (9 – 6)/(8 – 6)`
  `= 3/2`

 

`text(Using the point gradient formula,)`

`y – y_1` `= m(x – x_1)`
`y – 6` `= 3/2(x – 6)`
`y` `= 3/2 x – 3`

 

`text(When)\ y = 0,`

`0` `=3/2 x – 3`
`x` `= 2`

 

`:.\ text(Crosses)\ xtext{-axis at (2,0)}`

`=> D`

GEOMETRY, FUR1 2016 VCAA 1 MC

Consider the diagram below.

The shaded area, in square centimetres, is

  1. `35`
  2. `45`
  3. `60`
  4. `85`
  5. `95`
Show Answers Only

`A`

Show Worked Solution
`text(Shaded Area)` `= (1/2 xx 12 xx 10) – (5 xx5)`
  `= 60 – 25`
  `= 35\ text(cm²)`

`=> A`

MATRICES, FUR1 2016 VCAA 6 MC

Families in a country town were asked about their annual holidays.

Every year, these families choose between staying at home (H), travelling (T) and camping (C).

The transition diagram below shows the way families in the town change their holiday preferences from year to year.

 

A transition matrix that provides the same information as the transition diagram is

A. `{:(qquadqquadqquad\ text(from)),((qquadH,qquadT,qquadC)),([(0.30,0.75,0.65),(0.75,0.50,0.20),(0.65,0.20,0.60)]{:(H),(T),(C):}quad{:text(to):}):}` B. `{:(qquadqquadqquad\ text(from)),((qquadH,qquadT,qquadC)),([(0.30,0.30,0.40),(0.45,0.50,0),(0.25,0.20,0.60)]{:(H),(T),(C):}quad{:text(to):}):}`
       
C. `{:(qquadqquadqquad\ text(from)),((qquadH,qquadT,qquadC)),([(0.30,0.30,0.40),(0.45,0.50,0.20),(0.25,0.20,0.60)]{:(H),(T),(C):}quad{:text(to):}):}` D. `{:(qquadqquadqquad\ text(from)),((qquadH,qquadT,qquadC)),([(0.30,0.30,0.40),(0.45,0.50,0.20),(0.25,0.20,0.40)]{:(H),(T),(C):}quad{:text(to):}):}`
       
E. `{:(qquadqquadqquad\ text(from)),((qquadH,qquadT,qquadC)),([(0.30,0.45,0.25),(0.30,0.50,0.20),(0.40,0,0.60)]{:(H),(T),(C):}quad{:text(to):}):}`    
Show Answers Only

`B`

Show Worked Solution

`text(By elimination,)`

`H -> T = 0.45`

`:.\ text(not)\ A\ text(or)\ E`

`C -> T = 0`

`:.\ text(not)\ C\ text(or)\ D`

`=> B`

MATRICES, FUR1 2016 VCAA 2 MC

The matrix product `[(0,0,0,1,0),(0,0,1,0,0),(1,0,0,0,0),(0,1,0,0,0),(0,0,0,0,1)] xx [(text(L)),(text(E)),(text(A)),(text(P)),(text(S))]` is equal to

 

A.    `[(text(L)),(text(A)),(text(P)),(text(S)),(text(E))]` B.    `[(text(L)),(text(E)),(text(A)),(text(P)),(text(S))]` C.    `[(text(P)),(text(L)),(text(E)),(text(A)),(text(S))]` D.    `[(text(P)),(text(A)),(text(L)),(text(E)),(text(S))]` E.    `[(text(P)),(text(E)),(text(A)),(text(L)),(text(S))]`
Show Answers Only

`D`

Show Worked Solution

`[(text(P)),(text(A)),(text(L)),(text(E)),(text(S))]`

`=> D`

MATRICES, FUR1 2016 VCAA 1 MC

The transpose of `[(2,7,10),(13,19,8)]` is
 

A.    `[(13,19,8),(2,7,10)]`
B.    `[(10,7,2),(8,19,13)]`
C.    `[(2,13),(7,19),(10,8)]`
D.    `[(13,2),(19,7),(8,10)]`
E.    `[(8,10),(19,7),(13,2)]`
Show Answers Only

`C`

Show Worked Solution

`text(Transpose is a new matrix where)`

`text(the rows of 1 matrix become the)`

`text(columns.)`

`text(i.e.)\ \ x_(ij) => x_(ji)`

`[(2,7,10),(13,19,8)]^T` `= [(2,13),(7,19),(10,8)]`

`=> C`

CORE, FUR1 2016 VCAA 18 MC

The value of an annuity, `V_n`, after `n` monthly payments of $555 have been made, can be determined using the recurrence relation

`V_0 = 100\ 000,\ \ \ \ \ V_(n + 1) = 1.0025 V_n - 555`

The value of the annuity after five payments have been made is closest to

  1.   `$97\ 225`
  2.   `$98\ 158`
  3.   `$98\ 467`
  4.   `$98\ 775`
  5. `$110\ 224`
Show Answers Only

`C`

Show Worked Solution
`V_0` `= 100\ 000`
`V_1` `= 1.0025 xx 100\ 000 – 555 = 99\ 695`
`V_2` `= 1.0025 xx 99\ 695 – 555 = 99\ 389.23…`
`V_3` `= 1.0025 xx 99\ 389.24 – 555 = 99\ 082.71…`
`V_4` `= 1.0025 xx V_3 = 98\ 775.41…`
`V_5` `= 1.0025 xx V_4 = 98\ 467.35…`

 
`=> C`

CORE, FUR1 2016 VCAA 17 MC

Consider the recurrence relation below.

`A_0 = 2,\ \ \ \ \ A_(n + 1) = 3 A_n + 1`

The first four terms of this recurrence relation are

  1. `0, 2, 7, 22\ …`
  2. `1, 2, 7, 22\ …`
  3. `2, 5, 16, 49\ …`
  4. `2, 7, 18, 54\ …`
  5. `2, 7, 22, 67\ …`
Show Answers Only

`E`

Show Worked Solution
`A_0` `= 2\ \ (text(given))`
`A_1` `= 3(2) + 1 = 7`
`A_2` `= 3(7) + 1 = 22`
`A_3` `= 3(22) + 1 = 67`

 
`=> E`

CORE, FUR1 2016 VCAA 14-16 MC

The table below shows the long-term average of the number of meals served each day at a restaurant. Also shown is the daily seasonal index for Monday through to Friday.

 

Part 1

The seasonal index for Wednesday is 0.84

This tells us that, on average, the number of meals served on a Wednesday is

  1. 16% less than the daily average.
  2. 84% less than the daily average.
  3. the same as the daily average.
  4. 16% more than the daily average.
  5. 84% more than the daily average.

 

Part 2

Last Tuesday, 108 meals were served in the restaurant.

The deseasonalised number of meals served last Tuesday was closest to

  1.   `93`
  2. `100`
  3. `110`
  4. `131`
  5. `152`

 

Part 3

The seasonal index for Saturday is closest to

  1. `1.22`
  2. `1.31`
  3. `1.38`
  4. `1.45`
  5. `1.49`
Show Answers Only

`text(Part 1:)\ A`

`text(Part 2:)\ E`

`text(Part 3:)\ D`

Show Worked Solution

`text(Part 1)`

`1 – 0.84 = 0.16`

`:.\ text(A seasonal index of 0.84 tell us)`

`text(16% less meals are served.)`

`=> A`

 

`text(Part 2)`

`text{Deseasonalised number (Tues)}`

`= text(actual number)/text(seasonal index)`

`= 108/0.71`

`~~ 152`

`=> E`

 

`text(Part 3)`

`text(S)text(ince the same number of deseasonalised)`

`text(meals are served each day.)`

`text{S.I. (Sat)}/190` `= 1.10/145`
`text{S.I. (Sat)}` `= (1.10 xx 190)/145`
  `= 1.44…`

`=> D`

CORE, FUR1 2016 VCAA 13 MC

Consider the time series plot below.
 


 

The pattern in the time series plot shown above is best described as having

  1. irregular fluctuations only.
  2. an increasing trend with irregular fluctuations.
  3. seasonality with irregular fluctuations.
  4. seasonality with an increasing trend and irregular fluctuations.
  5. seasonality with a decreasing trend and irregular fluctuations.
Show Answers Only

`C`

Show Worked Solution

`text(The graph shows definite seasonality)`

`text(and no noticeable trend.)`

`=> C`

CORE, FUR1 2016 VCAA 1-2 MC

The blood pressure (low, normal, high) and the age (under 50 years, 50 years or over) of 110 adults were recorded. The results are displayed in the two-way frequency table below.
 

     

Part 1

The percentage of adults under 50 years of age who have high blood pressure is closest to

  1.  11%
  2.  19%
  3.  26%
  4.  44%
  5.  58%

Part 2

The variables blood pressure (low, normal, high) and age (under 50 years, 50 years or over) are

  1. both nominal variables.
  2. both ordinal variables.
  3. a nominal variable and an ordinal variable respectively.
  4. an ordinal variable and a nominal variable respectively.
  5. a continuous variable and an ordinal variable respectively.
Show Answers Only

`text(Part 1:)\ B`

`text(Part 2:)\ B`

Show Worked Solution

`text(Part 1)`

`text(Percentage)` `= text(Under 50 with high BP)/text(Total under 50)`
  `= 11/58`
  `~~ 19text(%)`

 
`=> B`

 

`text(Part 2)`

♦♦ Mean mark of Part 2: 31%.
MARKER’S COMMENT: Many students incorrectly identified the age (under 50, 50 or over) as nominal.

`text(Blood pressure is an ordinal variable)`

`text(because it is categorical data that can)`

`text(have an order.)`

`text(Under 50 and over 50, likewise, is an)`

`text(ordinal variable.)`

`=> B`

Measurement, NAP-B1-08

The minute hand is missing.
 


 

What time could this clock be showing?

`text(8 o'clock)` `text(half past 8)` `text(9 o'clock)` `text(half past 9)`
 
 
 
 
Show Answers Only

`text(half past 8)`

Show Worked Solution

`text(S)text(ince the hour hand is halfway between the 8 and 9,)`

`text(the clock could be showing half past 8.)`

Measurement, NAP-D1-12

Children at a Summer Camp are split into four colour teams, red, yellow, blue and green.

Which team has archery lessons first?

`text(Red)` `text(Yellow)` `text(Blue)` `text(Green)`
 
 
 
 
Show Answers Only

`text(Blue)`

Show Worked Solution

`text(Archery is earliest at 11:00 am.)`

`:.\ text(Blue has archery first.)`

Number and Algebra, NAP-D1-11

Melinda placed some shells in rows of 8.

She then put the same number of shells into bags of 6 and had some left over.

How many shells were left over?

`4` `3` `2` `1`
 
 
 
 
Show Answers Only

`2`

Show Worked Solution

`text(Total number of shells)`

`=8 xx 4`

`= 32`
 

`32 ÷ 6 = 5\ text(remainder 2)`

`:. 2\ text(shells were left over.)`

Geometry, NAP-D1-09

Kelly has sorted a number of shapes into groups.

How did Kelly sort her shapes?

 
 `text(by length of sides)`
 
 `text(by type of pattern)`
 
 `text(by number of sides)`
 
 `text(by height)`
Show Answers Only

`text(by number of sides)`

Show Worked Solution

`text(Every figure in each box has the same number)`

`text(of sides.)`

`=>\ text(Kelly has sorted them by number of sides.)`

Number and Algebra, NAP-D1-04

Chantelle showed this number on her calculator

She changed it so that it became this number.

What did Chantelle do to change 376 to 306?

 
 `text(added 7)`
 
 `text(subtracted 7)`
 
 `text(added 70)`
 
 `text(subtracted 70)`
Show Answers Only

`text(subtracted 70)`

Show Worked Solution

`376 – 70 = 306`

`=>\ text(subtracted 70)`

Measurement, NAP-E1-17

Rose called a restaurant on 3 November.

She booked dinner in exactly 3 weeks.
 

 
 

What date did Rose book the restaurant for?

 
 `text(6 November)`
 
 `text(10 November)`
 
 `text(23 November)`
 
 `text(24 November)`
Show Answers Only

`text(24 November)`

Show Worked Solution

`text(24 November)`

Measurement, NAP-F1-07

Six students line up side by side.

   

The teacher can make a line of shortest to tallest by swapping two students.

Which two students need to swap positions with each other?

 
 `text(Catherine and Justin)`
 
 `text(Catherine and Luke)`
 
 `text(Justin and Luke)`
 
 `text(Paddy and Luke)`
Show Answers Only

`text(Catherine and Luke)`

Show Worked Solution

`text(Catherine and Luke)`

Number and Algebra, NAP-I1-06

A boat hire shop has 5 paddle boats.

Each paddle boat can fit 4 people in it.

If all the paddle boats are hired out and have 4 people in them, how many people are in paddle boats altogether?

`5` `9` `15` `20`
 
 
 
 
Show Answers Only

`20`

Show Worked Solution
`text(Total people)` `=5 xx 4`
  `=20`

Statistics, NAP-I1-15

Cybil and Therese lived in different streets.

They were each counting different coloured cars that drove past their house one morning.

They drew a correct picture graph to show the number of coloured cars they saw altogether.

Which picture graph did they draw?  

 
 
 
 
Show Answers Only

Show Worked Solution

`text(Adding up the columns:)`

`text(White = 3, Blue = 5, Red = 4.)`

Number and Algebra, NAP-I1-14

The world record for the most push-ups ever completed in one hour is three thousand and ninety-two.

The number of push-ups can be written as:

`392` `3092` `3920` `30\ 092`
 
 
 
 
Show Answers Only

`3092`

Show Worked Solution

`text(Three thousand and ninety-two contains:)`

`=>\ text(3 “thousands”)`

`=>\ text(0 “hundreds”)`

`=>\ text(9 “tens”)`

`=>\ text(2 “ones”)`

`:. 3092`