SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Networks, STD2 N3 2020 HSC 30

The network diagram shows a series of water channels and ponds in a garden. The vertices `A`, `B`, `C`, `D`, `E`,  and `F` represent six ponds. The edges represent the water channels which connect the ponds. The numbers on the edges indicate the maximum capacity of the channels.
 


 

  1. Determine the maximum flow of the network.   (2 marks)

  2. A cut is added to the network, as shown.
     
       
    Is the cut shown a minimum cut? Give a reason for your answer.  (1 mark)

Show Answers Only
  1. `275`
  2. `text{Show Worked Solutions}`
Show Worked Solution

a.   `text(By trial and error, find min cut/max flow:)`

♦ Mean mark 41%.

 

  `text{Maximum Flow}` `= 50 + 75 + 100 +50`
    `= 275`

♦♦ Mean mark 28%.
b.      `text{Capacity of the cut}` `= 50 + 75 + 200`
    `= 325`

 
`therefore \ text{It is not a minimum cut (the cut in part (a) = 275 < 325)} `

Combinatorics, EXT1 A1 2020 HSC 14a

  1. Use the identity `(1 + x)^(2n) = (1 + x)^n(1 + x)^n`

     

    to show that
     
        `((2n),(n)) = ((n),(0))^2 + ((n),(1))^2 + … + ((n),(n))^2`,
     
    where `n` is a positive integer.  (2 marks)

  2. A club has `2n` members, with `n` women and `n` men.

     

    A group consisting of an even number `(0, 2, 4, …, 2n)` of members is chosen, with the number of men equal to the number of women.
     
    Show, giving reasons, that the number of ways to do this is `((2n),(n))`.  (2 marks)

  3. From the group chosen in part (ii), one of the men and one of the women are selected as leaders.

     

    Show, giving reasons, that the number of ways to choose the even number of people and then the leaders is
     

     

        `1^2 ((n),(1))^2 + 2^2((n),(2))^2 + … + n^2((n),(n))^2`.  (2 marks)

  4. The process is now reversed so that the leaders, one man and one woman, are chosen first. The rest of the group is then selected, still made up of an equal number of women and men.

     

    By considering this reversed process and using part (ii), find a simple expression for the sum in part (iii).  (2 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `text(See Worked Solutions)`
  3. `text(See Worked Solutions)`
  4. `n^2 xx \ ^(2n – 2)C_(n – 1)`
Show Worked Solution

i.   `text(Expand)\ \ (1 + x)^(2n):`

♦♦ Mean mark part (i) 26%.

`\ ^(2n)C_0 + \ ^(2n)C_1 x^2 + … + \ ^(2n)C_n x^n + … \ ^(2n)C_(2n) x^(2n)`

`=> text(Coefficient of)\ \ x^n = \ ^(2n)C_n`
 

`text(Expand)\ \ (1 + x)^n (1 + x)^n:`

`[\ ^nC_0 + \ ^nC_1 x + … + \ ^nC_n x^n][\ ^nC_0 + \ ^nC_1 x + … + \ ^nC_n x^n]`

`=> \ text(Coefficient of)\ \ x^n`

`= \ ^nC_0 · \ ^nC_n + \ ^nC_1 · \ ^nC_(n – 1) + … + \ ^nC_(n – 1) · \ ^nC_1 + \ ^nC_n · \ ^nC_0`

`= (\ ^nC_0)^2 + (\ ^nC_1)^2 + … + (\ ^nC_(n – 1))^2 + (\ ^nC_n)^2\ \ \ (\ ^nC_k = \ ^nC_(n – k))`
 

`text(Equating coefficients:)`

`\ ^(2n)C_n = (\ ^nC_0)^2 + (\ ^nC_1)^2 + … + (\ ^nC_n)^2`

♦♦ Mean mark part (ii) 23%.

 

ii.   `text(Number of men = Number of women)\ \ (M = W)`

`text(If)\ \ M = W = 0:`  `text(Ways) = \ ^nC_0 · \ ^nC_0 = (\ ^nC_0)^2`
`text(If)\ \ M = W = 1:`  `text(Ways) = \ ^nC_1 · \ ^nC_1 = (\ ^nC_1)^2`

`vdots`

`text(If)\ \ M = W = n:  text(Ways) = \ ^nC_n · \ ^nC_n = (\ ^nC_n)^2`
 

`:.\ text(Total combinations)`

`= (\ ^nC_0)^2 + (\ ^nC_1)^2 + … + (\ ^nC_n)^2`

`= \ ^(2n)C_n\ \ \ text{(from part (i))}`

 

iii.   `text(Let)\ \ M_L = text(possible male leaders)`

♦♦ Mean mark part (iii) 26%.

`text(Let)\ \ W_L = text(possible female leaders)`

`text(If)\ \ M = W = 0 => text(no leaders)`

`text(If)\ \ M = W = 1:  text(Ways) = \ ^nC_1 xx M_L xx \ ^nC_1 xx W_L = 1^2 (\ ^nC_1)^2`

`text(If)\ \ M = W = 2:  text(Ways) = \ ^nC_2 xx 2 xx \ ^nC_2 xx 2 = 2^2 (\ ^nC_2)^2`

`vdots`

`text(If)\ \ M = W = n:  text(Ways) = \ ^nC_n xx n xx \ ^nC_2 xx n = n^2 (\ ^nC_n)^2`
 

`:.\ text(Total combinations)`

`= 1^2(\ ^nC_1)^2 + 2^2(\ ^nC_2)^2 + … + n^2(\ ^nC_n)^2`

♦♦♦ Mean mark part (iv) 16%.

 

iv.  `text(If)\ \ M = W = 1:  text(Ways)` `= M_L xx \ ^(n – 1)C_0 xx W_L xx \ ^(n – 1)C_0`
    `= n xx \ ^(n – 1)C_0 xx n xx \ ^(n – 1)C_0`
    `= n^2(\ ^(n – 1)C_0)^2`
`text(If)\ \ M = W = 2:  text(Ways)` `= n xx \ ^(n – 1)C_1 xx n xx \ ^(n – 1)C_1`
  `= n^2(\ ^(n – 1)C_1)^2`

`vdots`

`text(If)\ \ M = W = n:\ text(Ways)` `= n xx \ ^(n – 1)C_(n – 1) xx n xx \ ^(n – 1)C_(n – 1)`
  `= n^2(\ ^(n – 1)C_(n – 1))^2`

 
`:.\ text(Total combinations)`

`= n^2(\ ^(n – 1)C_0)^2 + n^2(\ ^(n – 1)C_1)^2 + … + n^2(\ ^(n – 1)C_(n – 1))^2`

`= n^2 xx \ ^(2(n – 1))C_(n – 1)\ \ \ text{(using part (i))}`

`= n^2 xx \ ^(2n – 2)C_(n – 1)`

Networks, STD2 N3 2020 HSC 26

The preparation of a meal requires the completion of all activities `A` to `J`. The network diagram shows the activities and their completion times in minutes.
 


 

  1. What is the minimum time needed to prepare the meal?   (1 mark)

  2. List the activities which make up the critical path for this network.  (2 marks)

  3. Complete the table below, showing the earliest start time and float time for activities `A` and `G`  (2 marks)
     

Show Answers Only
  1. `46 \ text{minutes}`
  2. `C – D – E – F -H – I`
  3.  
Show Worked Solution

a.     `text{Scan forwards and backwards (to answer all parts):}`

♦♦ Mean mark part (a) 31%.
 


 

`text{Minimum time} = 46 \ text{minutes}`
 

b.     `C – D – E – F – H – I`

Mean mark part (b) 51%.

 

c.  `text{Scan backwards (see above):}`

♦♦ Mean mark part (c) 22%.
  

Financial Maths, STD2 F4 2020 HSC 29

Jana owns a share portfolio. Details of her share portfolio at 30 June 2020 are given in the table.
 

Jana received a total annual dividend of $149.52 from her share portfolio.

Calculate the number of shares Jana has in company  `XYZ`  on 30 June 2020.   (3 marks)

Show Answers Only

`348`

Show Worked Solution
`ABC \ text{Dividend}` `= text{Value of shares} xx text{dividend yield}`
  `= (200 xx 5.5) xx 0.06`
  `= $66.00`

♦ Mean mark 43%.
`XYZ \ text{Dividend}` `= 149.52 – 66.00`
  `= $83.52`

 

`text{Let} \ \ x = text{number of} \ XYZ \ text{shares}`

`83.52` `= text{Value of} \ XYZ \ text{shares} xx text{dividend yield}`
`83.52` `= (x xx 6.0) xx 0.04`
`6x` `= frac{83.52}{0.04}`
`therefore \ x` `= frac{2088}{6}`
  `= 348`

Statistics, STD2 S2 2020 HSC 28

Consider the following dataset.

`1        5        9         10        15`

Suppose a new value, `x`, is added to this dataset, giving the following.

      `1        5        9         10        15        x`

It is known that  `x`  is greater than 15. It is also known that the difference between the means of the two datasets is equal to ten times the difference between the medians of the two datasets.

Calculate the value of `x`.    (4 marks)

Show Answers Only

`38`

Show Worked Solution

`text{Dataset 1 : Median} = 9`

Mean mark 53%.

`text{Dataset 2 : Median} = frac{9 + 10}{2} = 9.5`

`:.\ text{Difference between means}`

`= 10 xx (9.5 – 9)`

`= 5`
 

`overset_ x_1 = frac{1 + 5 + 9 + 10 + 15}{5} = 8`
  
`therefore overset_ x_2 = 8 + 5 = 13`
 

`text{Sum of all data points in Dataset 2}`

`= 6 xx 13`

`= 78`
 

`78` `= 1 + 5 + 9 + 10 + 15 + x`
`therefore \ x` `= 78 – 40`
  `= 38`

Measurement, STD2 M1 2020 HSC 27

The shaded region on the diagram represents a garden. Each grid represents 5 m × 5 m.
 


 

  1. Use two applications of the trapezoidal rule to calculate the approximate area of the garden.   (3 marks)

  2. Should the answer to part (a) be more than, equal to or less than the actual area of the garden? Referring to the diagram above, briefly explain your answer.   (2 marks)

Show Answers Only
  1. `850 \ text{m}^2`
  2. `text{The estimate will be more than actual area}`
Show Worked Solution

a.     

`h = 4 xx 5 = 20 \ text{m}`

♦ Mean mark 47%.
`text{Area}` `= frac{h}{2} (x_1 + x_2) + frac{h}{2} (x_2 + x_3)`
   `= frac{20}{2} (25 + 20) + frac{20}{2} (20 + 20}`
  `= 450 + 400`
  `= 850 \ text{m}^2`

 

♦♦ Mean mark 23%.

b.     

`text{The trapezoidal rule captures the shaded area plus the}`

`text{the extra area highlighted above.}`

`therefore \ text{The estimate will be more than actual area}`

Calculus, EXT1 C3 2020 HSC 12e

Find the curve which satisfies the differential equation  `(dy)/(dx) = -x/y`  and passes through the point  `(1, 0)`.   (3 marks)

Show Answers Only

`x^2+y^2=1`

Show Worked Solution
COMMENT: Note the answer requires a curve equation, not a function.

`(dy)/(dx) = -x/y`

`int y\ dy = −int x\ dx`

`(y^2)/2 = -(x^2)/2 + c`

 
`text{Curve passes through (1, 0):}`

`0` `= -1/2 + c`
`c` `= 1/2`
`(y^2)/2` `= -(x^2)/2 + 1/2`
`y^2` `= -x^2 + 1`
`:.x^2+y^2` `= 1`

Algebra, STD2 A4 2020 HSC 24

There are two tanks on a property, Tank A and Tank B. Initially, Tank A holds 1000 litres of water and Tank B is empty.

  1. Tank A begins to lose water at a constant rate of 20 litres per minute.

     

    The volume of water in Tank A is modelled by  `V = 1000 - 20t`  where `V` is the volume in litres and  `t`  is the time in minutes from when the tank begins to lose water.

     

    On the grid below, draw the graph of this model and label it as Tank A.   (1 mark)
     

     

  2. Tank B remains empty until  `t=15`  when water is added to it at a constant rate of 30 litres per minute.
     By drawing a line on the grid (above), or otherwise, find the value of  `t`  when the two tanks contain the same volume of water.  (2 marks)

  3. Using the graphs drawn, or otherwise, find the value of  `t`  (where  `t > 0`) when the total volume of water in the two tanks is 1000 litres.  (1 mark)

Show Answers Only
  1.  `text{T} text{ank} \ A \ text{will pass trough (0, 1000) and (50, 0)}` 
      
  2. `29 \ text{minutes}`
  3. `45 \ text{minutes}`
Show Worked Solution

a.     `text{T} text{ank} \ A \ text{will pass trough (0, 1000) and (50, 0)}` 
 

 

b.   `text{T} text{ank} \ B \ text{will pass through (15, 0) and (45, 900)}`  
 

   

`text{By inspection, the two graphs intersect at} \ \ t = 29 \ text{minutes}`

 
c.   `text{Strategy 1}`

♦♦ Mean mark part (c) 22%.

`text{By inspection of the graph, consider} \ \ t = 45`

`text{T} text{ank A} = 100 \ text{L} , \ text{T} text{ank B} =900 \ text{L} `

`:.\ text(Total volume = 1000 L when  t = 45)`
  

`text{Strategy 2}`

`text{Total Volume}` `=text{T} text{ank A} + text{T} text{ank B}`
`1000` `= 1000 – 20t + (t – 15) xx 30`
`1000` `= 1000 – 20t + 30t – 450 `
`10t` `= 450`
`t` `= 45 \ text{minutes}`

Trigonometry, 2ADV T3 2020 HSC 31

The population of mice on an isolated island can be modelled by the function.

`m(t) = a sin (pi/26 t) + b`,

where  `t`  is the time in weeks and  `0 <= t <= 52`. The population of mice reaches a maximum of 35 000 when  `t=13`  and a minimum of 5000 when  `t = 39`. The graph of  `m(t)`  is shown.
 

  1. What are the values of `a` and `b`?  (2 marks)

  2. On the same island, the population of cats can be modelled by the function
     
    `\ \ \ \ \ c(t) = −80cos(pi/26 (t - 10)) + 120`
     
    Consider the graph of  `m(t)`  and the graph of  `c(t)`.

     

    Find the values of  `t, \ 0 <= t <= 52`, for which both populations are increasing.  (3 marks)

  3. Find the rate of change of the mice population when the cat population reaches a maximum.  (2 marks)

Show Answers Only
  1. `a = 15\ 000, b = 20\ 000`
  2. `text(Both populations are increasing when)\ 10 < t < 13`
  3. `\text(– 643 mice per week)`
Show Worked Solution
a.    `b` `= (35\ 000 + 5000)/2`
    `= 20\ 000`

 

`a` `=\ text(amplitude of sin graph)`
  `= 35\ 000 – 20\ 000`
  `= 15\ 000`

 

b.   `text(By inspection of the)\ \ m(t)\ \ text(graph)`

♦♦ Mean mark part (b) 30%.

`m^{′}(t) > 0\ \ text(when)\ \ 0 <= t < 13\ \ text(and)\ \ 39 < t <= 52`

`text(Sketch)\ \ c(t):`

`text(Minimum)\ \ (cos0)\ \ text(when)\ \ t = 10`

`text(Maximum)\ \ (cospi)\ \ text(when)\ \ t = 36`

`:. c^{′}(t) > 0\ \ text(when)\ \ 10 < t < 36`

`:. text(Both populations are increasing when)\ \ 10 < t < 13`

 

c.   `c(t)\ text(maximum when)\ \ t = 36`

♦♦♦ Mean mark part (c) 27%.
`m(t)` `= 15\ 000 sin(pi/26 t) + 20\ 000`
`m^{′}(t)` `= (15\ 000pi)/26 cos(pi/26 t)`
`m^{′}(36)` `= (15\ 000pi)/26 · cos((36pi)/26)`
  `= -642.7`

 
`:.\ text(Mice population is decreasing at 643 mice per week.)`

Measurement, STD2 M7 2020 HSC 23

In a tropical drink, the ratio of pineapple juice to mango juice to orange juice is 15 : 9 : 4 .

  1. How much orange juice is needed if the tropical drink is to contain 3 litres of pineapple juice?  (2 marks)

  2. The internal dimensions of a drink container, in the shape of a rectangular prism, are shown.
     
     
         
     
    To completely fill the container with the tropical drink, how many litres of mango juice are required. (3 marks)

Show Answers Only
  1. `0.8 \ text{L}`
  2. `9\ text{L}`
Show Worked Solution
a.    `text(15 parts)` `= 3\ text(L)`
  `text(1 part)` `=3/15`
    `=0.2\ text(L)`

 

`:.\ text(4 parts)` `=4 xx 0.2`  
  `=0.8\ text(L)`  

 

Mean mark 51%.
b.      `text{Volume of container}` `= 40 xx 20 xx 35`
    `= 28 \ 000 \ text{cm}^3`

 
`1 \ text{mL} \ to \ 1 \ text{cm}^3`

`⇒ \ 28 \ 000 \ text{mL of tropical drink}`

`therefore \ text{Mango juice required}` `=text(Mango parts)/text(Total parts) xx 28\ 000`
  `= frac{9}(28} xx 28 \ 000`
  `= 9000 \ text{mL}`
  `=9\ text(L)`

Statistics, 2ADV S2 2020 HSC 27

A cricket is an insect. The male cricket produces a chirping sound.

A scientist wants to explore the relationship between the temperature in degrees Celsius and the number of cricket chirps heard in a 15-second time interval.

Once a day for 20 days, the scientist collects data. Based on the 20 data points, the scientist provides the information below.

  • A box-plot of the temperature data is shown.
     
       
  • The mean temperature in the dataset is 0.525°C below the median temperature in the dataset.
  • A total of 684 chirps was counted when collecting the 20 data points.

The scientist fits a least-squares regression line using the data `(x, y)`, where `x` is the temperature in degrees Celsius and `y` is the number of chirps heard in a 15-second time interval. The equation of this line is

`y = −10.6063 + bx`,

where `b` is the slope of the regression,

The least-squares regression line passes through the point  `(barx, bary)`, where  `barx`  is the sample mean of the temperature data and  `bary`  is the sample mean of the chirp data.

Calculate the number of chirps expected in a 15-second interval when the temperature is 19° Celsius. Give your answer correct to the nearest whole number.  (5 marks)

Show Answers Only

`29\ text(chirps)`

Show Worked Solution

`y = −10.6063 + bx`

♦ Mean mark 46%.

`text(Find)\ b:`

`text(Line passes through)\ \ (barx, bary)`

`barx` `= 22 – 0.525`
  `= 21.475`

 

`bary` `= text(total chirps)/text(number of data points)`
  `= 684/20`
  `= 34.2`

 

`34.2` `= −10.6063 + b(21.475)`
`:.b` `= 44.8063/21.475`
  `~~ 2.0864`

 

`text(If)\ \ x = 19,`

`y` `= −10.6063 + 2.0864 xx 19`
  `= 29.03`
  `= 29\ text(chirps)`

Statistics, 2ADV S3 2020 HSC 28

In a particular country, the hourly rate of pay for adults who work is normally distributed with a mean of $25 and a standard deviation of $5.

  1. Two adults who both work are chosen at random.

     

    Find the probability that at least one of them earns between $15 and $30 per hour.  (3 marks)

  2. The number of adults who work is equal to three times the number of adults who do not work.

     

    One adult is chosen at random.

     

    Find the probability that the chosen adult works and earn more than $25 per hour.  (2 marks)

Show Answers Only
  1. `0.965775`
  2. `3/8`
Show Worked Solution

`ztext(-score)\ ($15) = (x – mu)/sigma = (15 – 25)/5 = −2`

♦ Mean mark part (a) 40%.

`ztext(-score)\ ($30) = (30 -25)/5 = 1`
 

`text(Percentage of scores where)\  −2 <= z <= 1`

`= 81.5text(%)`
 

`P(text(at least one earns between $15 – $30))`

`= 1 – P(text(neither))`

`= 1 – (1-0.815)^2`

`=1-0.185^2`

`= 0.965775`


b.   `P(text(works)) = 3/4, \ P(text(earns) > $25) = 1/2`

`:. P(text(works and earns) > $25)`

`= 3/4 xx 1/2`

`= 3/8`

Functions, 2ADV F1 2020 HSC 24

The circle of  `x^2-6x + y^2 + 4y-3 = 0`  is reflected in the `x`-axis.

Sketch the reflected circle, showing the coordinates of the centre and the radius.  (3 marks)

Show Answers Only

Show Worked Solution
`x^2-6x + y^2 + 4y-3` `= 0`
`x^2-6x + 9 + y^2 + 4y + 4-16` `= 0`
`(x-3)^2 + (y + 2)^2` `= 16`

 
`=>\  text{Original circle has centre (3, − 2), radius = 4}`

`text(Reflect in)\ xtext(-axis):`

♦ Mean mark 48%.

`text{Centre (3, − 2) → (3, 2)}`
 

Calculus, 2ADV C4 2020 HSC 30

The diagram shows two parabolas  `y = 4x - x^2`  and  `y = ax^2`, where  `a > 0`. The two parabolas intersect at the origin, `O`, and at `A`.
 


 

  1. Show that the `x`-coordinate of  `A`  is  `4/(a + 1)`.  (2 marks)

  2. Find the value of  `a`  such that the shaded area is `16/3`.  (4 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `sqrt2 – 1`
Show Worked Solution

a.   `text(Intersection occurs when)`

`4x – x^2` `= ax^2`
`x^2(a + 1) – 4x` `= 0`
`x[x(a + 1) – 4]` `= 0`
`x(a+1)-4` `=0\ \ \ text(or)`   `x=0`
`:. x_A` `=4/(a + 1)`  

♦ Mean mark part (b) 48%.

 

b.    `text(Area)` `= int_0^(4/(a + 1)) 4x – x^2\ dx – int_0^(4/(a + 1)) ax^2\ dx`
  `16/3` `= int_0^(4/(a + 1)) 4x – (1 + a)x^2\ dx`
  `16/3` `= [2x^2 – ((1 + a)/3) x^3]_0^(4/(a + 1))`
  `16/3` `= 2(4/(a + 1))^2 – ((1 + a)/3)(4/(a + 1))^3`
  `16/3` `= 32/((a + 1)^2) – 64/3 · 1/((a + 1)^2)`
  `16` `= 96/((a + 1)^2) – 64/((a + 1)^2)`
`16(a + 1)^2` `= 32`
`(a + 1)^2` `= 2`
`a + 1` `= sqrt2,\ \ \ (a > 0)`
`:. a` `= sqrt2 – 1`

Calculus, 2ADV C3 2020 HSC 29

The diagram shows the graph of  `y = c ln x, \ c > 0`.
 

  1. Show that the equation of the tangent to  `y = c ln x`  at  `x = p`, where  `p > 0`, is
     
    `\ \ \ \ \ y = c/p x - c + c ln p`.  (2 marks)

  2. Find the value of `c` such that the tangent from part (a) has a gradient of 1 and passes through the origin.  (2 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `c = e`
Show Worked Solution

a.   `y = c ln x`

`(dy)/(dx) = c/x`

`text(At)\ x = p,`

`m_text(tang) = c/p`

`text(T)text(angent passes through)\ (p, c ln p)`

 
`:.\ text(Equation of tangent)`

`y – c ln p` `= c/p (x – p)`
`y` `= c/p x – c + c ln p`

 

b.   `text(If)\ m_text(tang) = 1,`

♦ Mean mark part (b) 40%.
`c/p` `= 1`
`c` `= p`

 
`text(If tangent passes through)\ (0, 0)`

`0` `= −c + c ln c`
`0` `= c(ln c – 1)`

 
`ln c = 1\ \ (c > 0)`

`:. c = e`

Financial Maths, STD2 F5 2020 HSC 34

Tina inherits $60 000 and invests it in an account earning interest at a rate of 0.5% per month. Each month, immediately after the interest has been paid, Tina withdraws $800.

The amount in the account immediately after the `n`th withdrawal can be determined using the recurrence relation

`A_n = A_(n - 1)(1.005) - 800`,

where `n = 1, 2, 3, …`  and  `A_0 = 60\ 000`

  1. Use the recurrence relation to find the amount of money in the account immediately after the third withdrawal.  (2 marks)

  2. Calculate the amount of interest earned in the first three months.  (2 marks)

Show Answers Only
  1. `$58\ 492.49`
  2. `$892.49`
Show Worked Solution

♦ Mean mark part (a) 41%.
a.    `A_1` `= 60\ 000(1.005) – 800 = $59\ 500`
  `A_2` `= 59\ 500(1.005) – 800 = $58\ 997.50`
  `A_3` `= 58\ 997.50(1.005) – 800 = $58\ 492.49`

 

b.   `text{Amount (not interest)}`

♦♦ Mean mark part (b) 33%.

`= 60\ 000 – (3 xx 800)`

`= $57\ 600`
 

`:.\ text(Interest earned in 3 months)`

`= A_3 – 57\ 600`

`= 58\ 492.49 – 57\ 600`

`= $892.49`

Financial Maths, 2ADV M1 2020 HSC 26

Tina inherits $60 000 and invests it in an account earning interest at a rate of 0.5% per month. Each month, immediately after the interest has been paid, Tina withdraws $800.

The amount in the account immediately after the `n`th withdrawal can be determined using the recurrence relation

`A_n = A_(n - 1)(1.005) - 800`,

where `n = 1, 2, 3, …`  and  `A_0 = 60\ 000`

  1. Use the recurrence relation to find the amount of money in the account immediately after the third withdrawal.  (2 marks)

  2. Calculate the amount of interest earned in the first three months.  (2 marks)

  3. Calculate the amount of money in the account immediately after the 94th withdrawal.  (3 marks) 

Show Answers Only
  1. `$58\ 492.49`
  2. `$892.49`
  3. `$187.85`
Show Worked Solution
a.    `A_1` `= 60\ 000(1.005) – 800 = $59\ 500`
  `A_2` `= 59\ 500(1.005) – 800 = $58\ 997.50`
  `A_3` `= 58\ 997.50(1.005) – 800 = $58\ 492.49`

 

b.   `text{Amount (not interest)}`

`= 60\ 000 – (3 xx 800)`

`= $57\ 600`
 

`:.\ text(Interest earned in 3 months)`

`= A_3 – 57\ 600`

`= 58\ 492.49 – 57\ 600`

`= $892.49`
 

c.   `A_1 = 60\ 000(1.005) – 800`

`A_2` `= [60\ 000(1.005) – 800](1.005) – 800`
  `= 60\ 000(1.005)^n – 800(1.005 + 1)`
`vdots`  
`A_n` `= 60\ 000(1.005)^n – 800(1 + 1.005 + … + 1.005^(n – 1))`
`A_94` `= 60\ 000(1.005)^94 – 800\ underbrace((1 + 1.005 + … + 1.005^93))_(text(GP where)\ a = 1,\ r = 1.005,\ n = 94)`
  `= 60\ 000(1.005)^94 – 800 ((1(1.005^94 – 1))/(1.005 – 1))`
  `= 60\ 000(1.005)^94 – 160\ 000(1.005^94 – 1)`
  `= $187.85`

Algebra, STD2 A4 2020 HSC 19

A fence is to be built around the outside of a rectangular paddock. An internal fence is also to be built.

The side lengths of the paddock are `x` metres and `y` metres, as shown in the diagram.
 

 
A total of 900 metres of fencing is to be used. Therefore  `3x + 2y = 900`.
 
The area, `A`, in square metres, of the rectangular paddock is given by  `A =450x - 1.5x^2`.

The graph of this equation is shown.
  

  1. If the area of the paddock is `30 \ 000\ text(m)^2`, what is the largest possible value of `x`?   (1 mark)

  2. Find the values of `x` and `y` so that the area of the paddock is as large as possible.   (2 marks)

  3. Using your value from part (b), find the largest possible area of the paddock.   (1 mark)

Show Answers Only
  1. `200 \ text(m)`
  2. `x = 150 \ text(m and) \ y = 225 \ text(m)`
  3. `33 \ 750 \ text(m)^2`
Show Worked Solution

a.     `text(From the graph, an area of)\ 30\ 000\ text(m)^2`

♦ Mean mark part (a) 39%.

  `text(can have an)\ x text(-value of)\ \ x=100 or 200\ text(m.)`

`:. x_text(max) = 200 text(m)`
 

b.    `A_text(max) \ text(occurs when) \ \ x = 150`

♦♦ Mean mark part (b) 34%.

`text(Substitute)\ \ x=150\ \ text(into)\ \ 3x + 2y = 900:`

`3 xx 150 + 2y` `= 900`
`2y` `= 450`
`y` `= 225`

 
`therefore \ text(Maximum area when) \ \ x = 150 \ text(m  and) \ \ y = 225 \ text(m)`

♦ Mean mark part (c) 40%.
c.    `A_(max)` `= xy`
    `= 150 xx 225`
    `= 33 \ 750 \ text(m)^2`

Probability, 2ADV S1 2020 HSC 14

History and Geography are two of the subjects students may decide to study. For a group of 40 students, the following is known.

    • 7 students study neither History nor Geography
    • 20 students study History
    • 18 students study Geography
  1. A student is chosen at random. By a using a Venn diagram, or otherwise, find the probability that the student studies both History and Geography.  (2 marks)

  2. A students is chosen at random. Given that the student studies Geography, what is the probability that the student does NOT study History?  (1 mark)

  3. Two different students are chosen at random, one after the other. What is the probability that the first student studies History and the second student does NOT study History?  (2 marks)

Show Answers Only
  1.  
  2. `13/18`
  3. `10/39`
Show Worked Solution
a.   
`P(text(H and G))` `= 5/40`
  `= 1/8`

 

♦ Mean mark (b) 49%.
b.    `P(bartext(H) | text(G))` `= (P(bartext(H) ∩ text(G)))/(Ptext{(G)})`
    `= 13/18`

 

c.    `P(text(H), bartext(H))` `= 20/40 xx 20/39`
    `= 10/39`

Calculus, 2ADV C3 2020 HSC 25

A landscape gardener wants to build a garden in the shape of a rectangle attached to a quarter-circle. Let `x` and `y` be the dimensions of the rectangle in metres, as shown in the diagram.
 


 

The garden bed is required to have an area of 36 m² and to have a perimeter which is as small as possible. Let `P` metres be the perimeter of the garden bed.

  1. Show that  `P = 2x + 72/x`.  (3 marks)

  2. Find the smallest possible perimeter of the garden bed, showing why this is the minimum perimeter.  (4 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `24\ text(m)`
Show Worked Solution
a.    `text(Area)` `= xy + 1/4 pir^2`
  `36` `= xy + 1/4 pix^2`
  `xy` `= 36 – (pix^2)/4`
  `y` `= 36/x – (pix)/4`

♦ Mean mark part (a) 47%.

 

`:. P` `= 2x + 2y + 1/4(2pix)`
  `= 2x + 2(36/x – (pix)/4) + (pix)/2`
  `= 2x + 72/x – (pix)/2 + (pix)/2`
  `= 2x + 72/x`

 

b.   `P = 2x + 72/x`

`(dP)/(dx)` `= 2 – 72x^(−2)`
`(d^2P)/(dx^2)` `= 144x^(−3)`

 
`text(Max or min when)\ \ (dP)/(dx) = 0:`

`2 – 72/(x^2)` `= 0`
`2x^2` `= 72`
`x^2` `= 36`
`x` `= 6,\ \  (x > 0)`

 

`text(When)\ \ x = 6,`

`(d^2P)/(dx^2) = 144/(6^3) = 2/3 > 0`

 
`=>\  text(MIN at)\ x = 6`

`:. P_text(min)` `= 2 xx 6 + 72/6`
  `= 24\ text(m)`

Statistics, 2ADV S3 2020 HSC 23

A continuous random variable, `X`, has the following probability density function.
 

`f(x) = {(sin x, text(for)\ \ 0 <= x <= k),(0, text(for all other values of)\ x):}`
 

  1. Find the value of `k`.  (2 marks)

  2. Find  `P(X <= 1)`. Give your answer correct to four decimal places.  (2 marks)

Show Answers Only
  1. `pi/2`
  2. `0.4597\ \ (text(to 2 d.p.))`
Show Worked Solution
a.    `int_0^k sin x` `= 1`
  `[−cos x]_0^k` `= 1`
  `−cos k + cos 0` `= 1`
  `−cos k` `= 0`
  `cos k` `= 0`
  `k` `= pi/2`

 

♦ Mean mark part (b) 44%.
b.    `P(X <= 1)` `= int_0^1 sin x\ dx`
    `= [−cos x]_0^1`
    `= −cos1 + cos0`
    `= 1 – cos1`
    `= 0.45969…`
    `= 0.4597\ \ (text(to 4 d.p.))`

Calculus, 2ADV C3 2020 HSC 21

Hot tea is poured into a cup. The temperature of tea can be modelled by  `T = 25 + 70(1.5)^(−0.4t)`, where `T` is the temperature of the tea, in degrees Celsius, `t` minutes after it is poured.

  1. What is the temperature of the tea 4 minutes after it has been poured?  (1 mark)

  2. At what rate is the tea cooling 4 minutes after it has been poured?  (2 marks)

  3. How long after the tea is poured will it take for its temperature to reach 55°C?  (3 marks)

Show Answers Only
  1. `61.6\ \ (text(to 1 d.p.))`
  2. `−5.9^@text(C/min)`
  3. `5.2\ text(minutes  (to 1 d.p.))`
Show Worked Solution
a.    `T` `= 25 + 70(1.5)^(−0.4 xx 4)`
    `= 61.58…`
    `= 61.6\ \ (text(to 1 d.p.))`

 

b.    `(dT)/(dt)` `= 70 log_e(1.5) xx −0.4(1.5)^(−0.4t)`
    `= −28log_e(1.5)(1.5)^(−0.4t)`

 

`text(When)\ \ t = 4,`

`(dT)/(dt)` `= −28log_e(1.5)(1.5)^(−1.6)`
  `= −5.934…`
  `= −5.9^@text(C/min  (to 1 d.p.))`

 

c.   `text(Find)\ \ t\ \ text(when)\ \ T = 55:`

♦ Mean mark part (c) 44%.
`55` `= 25 + 70(1.5)^(−0.4t)`
`30` `= 70(1.5)^(0.4t)`
`(1.5)^(−0.4t)` `= 30/70`
`−0.4t log_e(1.5)` `= log_e\ 3/7`
`−0.4t` `= (log_e\ 3/7)/(log_e (1.5))`
`:. t` `= (−2.08969)/(−0.4)`
  `= 5.224…`
  `= 5.2\ text(minutes  (to 1 d.p.))`

Probability, STD2 S2 2020 HSC 15 MC

The top of a rectangular table is divided into 8 equal sections as shown.
 

A standard die with faces labelled 1 to 6 is rolled onto the table. The die is equally likely to land in any of the 8 sections of the table. If the die does not land entirely in one section of the table, it is rolled again.

A score is calculated by multiplying the value shown on the top face of the die by the number shown in the section of the table where the die lands.

What is the probability of getting a score of 6?

  1. `frac{1}{48}`
  2. `frac{1}{12}`
  3. `frac{1}{8}`
  4. `frac{1}{6}`
Show Answers Only

`B`

Show Worked Solution

`text{Strategy 1}`

♦ Mean mark 40%.

`text{Combinations that score 6:}`

`4 \ text{combinations score} \ 6`

`therefore \ P(6)` `= 4 xx frac{1}{8} xx frac{1}{6}`
  `= frac{1}{12}`

 

`text{Strategy 2}`

`Ptext{(6)}` `= Ptext{(T1)}Ptext{(D6)} + Ptext{(T2)}Ptext{(D3)} + Ptext{(T3)}Ptext{(D2)} + Ptext{(T6)}Ptext{(D1)}`
  `= frac{1}{8} xx frac{1}{6} + frac{1}{8} xx frac{1}{6} + frac{1}{8} xx frac{1}{6} + frac{1}{8} xx frac{1}{6}`
  `= 4 xx frac{1}{8} xx frac{1}{6}`
  `= frac{1}{12}`

 
`=> \ B`

Financial Maths, STD2 F5 2020 HSC 14 MC

An annuity consists of ten payments, each equal to $1000. Each payment is made on 30 June each year from 2021 through to 2030 inclusive.

The rate of compound interest is 5% per annum.

The present value of the annuity is calculated at 30 June 2020.

The future value of the annuity is calculated at 30 June 2030.

Without performing any calculations, which of the following statements is true?

  1. Present value of the annuity  <  $10 000  <  future value of the annuity
  2. $10 000  <  present value of the annuity  <  future value of the annuity
  3. Future value of the annuity  <  $10 000  <  present value of the annuity
  4. $10 000  <  future value of the annuity  <  present value of the annuity
Show Answers Only

`A`

Show Worked Solution

Mean mark 53%.

`PV\ text{(30 June 2020)}  < $10\ 000\ \ text{(each payment discounted to 30-Jun-20 value)}`

`FV\ text{(30 June 2030)}  => text{annuity has received}\ \  10 xx $1000`

`text{payments plus interest}`

`therefore \ FV\ text{(30 June 2030)} \ > \ $10\ 000 `
 

`=> \ A`

Calculus, 2ADV C4 2020 HSC 18

  1. Differentiate  `e^(2x) (2x + 1)`.  (2 marks)

  2. Hence, find  `int(x + 1)e^(2x)\ dx`.  (1 marks)

Show Answers Only
  1. `4e^(2x)(x + 1)`
  2. `1/4 e^(2x)(2x + 1) + c`
Show Worked Solution
a.    `y` `= e^(2x) (2x + 1)`
  `(dy)/(dx)` `= 2e^(2x)(2x + 1) + 2e^(2x)`
    `= 2e^(2x)(2x + 2)`
    `= 4e^(2x)(x + 1)`

♦ Mean mark part (b) 40%.

 

b.    `int(x + 1)e^(2x)dx` `= 1/4 int 4e^(2x)(x + 1)`
    `= 1/4 e^(2x)(2x + 1) + c`

Calculus, 2ADV C3 2020 HSC 8 MC

The graph of  `y = f(x)`  is shown.
 

Which of the following inequalities is correct?

  1. `f^{″}(1) < 0 < f^{′}(1) < f(1)`
  2. `f^{″}(1) < 0 < f(1) < f^{′}(1)`
  3. `0 < f^{″}(1) < f^{′}(1) < f(1)`
  4. `0 < f^{″}(1) < f(1) < f^{′}(1)`
Show Answers Only

`A`

Show Worked Solution

`y = f(x)\ text(is concave down at)\ \ x = 1`

Mean mark 52%.

`f^{″}(1) < 0`

`=>\ text(Eliminate C and D.)`
 
 

`text(T)text(angent)\ => y=mx+b`

COMMENT: Note the concavity causes any tangent to cut the positive y-axis. No y-axis scale is therefore required.

`text(At)\ \ x = 1, m_text(tang) = f^{′}(1)`

`text(At intersection:)`

`mx+b` `=f(1)`  
`f^{′}(1) xx 1 + b` `=f(1)`  
`:. f^{′}(1)` `<f(1),\ \ \  (b>0)`  

 
`:. f^{″}(1) < 0 < f^{′}(1) < f(1)`

`=>A`

Calculus, 2ADV C4 2020 HSC 7 MC

The diagram show the graph  `y = f(x)`, which is made up of line segments and a semicircle.
 

What is the value of  `int_0^12 f(x)\ dx`?

  1.  `24 + 2pi`
  2.  `24 + 4pi`
  3.  `30 + 2pi`
  4.  `30 + 4pi`
Show Answers Only

`A`

Show Worked Solution

`text(Consider the interval between)\ \ x=8 and x=12:`

`text(Area above and below the)\ xtext(-axis are equal.)`

`int_8^12 f(x) = 0`

♦ Mean mark 48%.
 

`:. int_0^12 f(x)\ dx` `= int_0^8 f(x)\ dx`
  `=\ text(Area of rectangle + area of semi-circle)`
  `= 8 xx 3 + 1/2 xx pi xx 2^2`
  `= 24 + 2pi`

 
`=>A`

Financial Maths, STD2 F4 2020 HSC 11 MC

An asset is depreciated using the declining-balance method with a rate of depreciation of 8% per half year. The asset was bought for $10 000.

What is the salvage value of the asset after 5 years?

  1.  $1749.01
  2.  $4182.12
  3.  $4343.88
  4.  $6590.82
Show Answers Only

`C`

Show Worked Solution

♦ Mean mark 43%.
COMMENT: 8% depreciation is applicable every 6 months here (n=10). Read carefully!

`V_0 = 10\ 000 \ , \ r = 0.08 \ , \ n = 10`

`S` `= V_0 (1 – r)^n`
  `= 10\ 000 (1 – 0.08)^10`
  `= 10\ 000 (0.92)^10`
  `= $ 4343.88`

 
`=> \ C`

Algebra, STD2 A2 2020 HSC 10 MC

A plumber charges a call-out fee of $90 as well as $2 per minute while working.

Suppose the plumber works for `t` hours.

Which equation expresses the amount the plumber charges ($`C`) as a function of time (`t` hours)?

  1.  `C = 2 + 90t`
  2.  `C = 90 + 2t`
  3.  `C = 120 + 90t`
  4.  `C = 90 + 120t`
Show Answers Only

`D`

Show Worked Solution

♦ Mean mark 42%.

`text(Hourly rate)\ = 60 xx 2=$120`

`:. C = 90 + 120t`

`=>D`

Networks, STD2 N2 2020 HSC 9 MC

Team `A` and Team `B` have entered a chess competition.

Team `A` and `B` have three members each. Each member of Team `A` must play each member of Team `B` once.

Which of the following network diagrams could represent the chess games to be played?
 

 

 

  
Show Answers Only

`B`

Show Worked Solution

♦ Mean mark 38%.

`text(Vertices = players)`

`text(Edges = games between 2 players)`

`text(S)text(ince each player plays once against the three players)`

`text(in the other team, each vertex must be degree 3.)`

`=> \ B`

Statistics, STD2 S1 2020 HSC 7 MC

Which histogram best represents a dataset that is positively skewed?

 
 
Show Answers Only

`A`

Show Worked Solution

♦♦ Mean mark 32%.

`text(Positive skew occurs when the tail on the)`

`text{histogram is longer on the right-hand}`

`text{(positive) side.}`

`=> \ A`

Measurement, STD2 M1 2020 HSC 5 MC

A plant stem is measured to be 16.0 cm, correct to one decimal place.

What is the percentage error in this measurement?

  1.  0.3125%
  2.  0.625%
  3.  3.125%
  4.  6.25%
Show Answers Only

`A`

Show Worked Solution

♦ Mean mark 41%.

`text{Absolute error} = 1/2 xx \text{precision} = 1/2 xx 0.1 = 0.05\ text{cm}`

`%  text(error)` `= frac(0.05)(16.0) xx 100`
  `= 0.3125%`

 
`=> \ A`

Measurement, STD2 M1 2020 HSC 2 MC

What is 0.002073 expressed in standard form with two significant figures?

  1. `2.07 xx 10^(-2)`
  2. `2.1 xx 10^(-2)`
  3. `2.07 xx 10^(-3)`
  4. `2.1 xx 10^(-3)`
Show Answers Only

`D`

Show Worked Solution

♦♦ Mean mark 35%.
COMMENT: A notable knowledge gap flagged by this result.
`0.002073` `= 2.073 xx 10^(-3)`  
  `=2.1 xx 10^(-3)\ \ \ text{(to 2 sig fig)}`  

 
`=> D`

Mechanics, EXT2 M1 EQ-Bank 4

A torpedo with a mass of 80 kilograms has a propeller system that delivers a force of `F` on the torpedo, at maximum power. The water exerts a resistance on the torpedo proportional to the square of the torpedo's velocity `v`.

  1. Explain why  `(dv)/(dt) = 1/80 (F - kv^2)`
     
    where `k` is a positive constant.  (1 mark)

  2. If the torpedo increases its velocity from  `text(10 ms)\ ^(−1)`  to  `text(20 ms)\ ^(−1)`, show that the distance it travels in this time, `d`, is given by
     
         `d = 40/k log_e((F - 100k)/(F - 400k))`  (3 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `text(See Worked Solutions)`
Show Worked Solution

i.   `R ∝ v^2`

`R = −kv^2\ \ (k\ text{is positive constant})`

`text(Newton’s 2nd Law:)`

`text(Net Force)= mddotx` `= F – R`
`80ddotx` `= F – kv^2`
`ddotx` `= 1/80 (F – kv^2)`
`(dv)/(dt)` `= 1/80 (F – kv^2)`

 

ii.    `v · (dv)/(dx)` `= 1/80 (F – kv^2)`
  `(dv)/(dx)` `= (F – kv^2)/(80v)`
  `(dx)/(dv)` `= (80v)/(F – kv^2)`
  `x` `= −40 int (−2v)/(F – kv^2)\ dv`
    `= −40/k log_e (F – kv^2) + C`

 

`text(When)\ \ v = 10:`

`x_1 = −40/k log_e (F – 100k) + C`
 

`text(When)\ \ v = 20:`

`x_2 = −40/k log_e (F – 400k) + C`
 

`d` `= x_2 – x_1`
  `= −40/k log_e (F – 400k) + 40/k log_e (F – 100k)`
  `= 40/k log_e ((F – 100k)/(F – 400k))`

Mechanics, EXT2 M1 EQ-Bank 2

A particle with mass `m` moves horizontally against a resistance force `F`, equal to  `mv(1 + v^2)`  where `v` is the particle's velocity.

Initially, the particle is travelling in a positive direction from the origin at velocity `T`.

  1. Show that the particle's displacement from the origin, `x`, can be expressed as
     
         `x = tan^(-1)((T - v)/(1 + Tv))`  (2 marks)

     

  2. Show that the time, `t`, when the particle is travelling at velocity `v`, is given by
     
         `t = 1/2 log_e ((T^2(1 + v^2))/(v^2(1 + T^2)))`  (4 marks)

     

  3. Express `v^2` as a function of `t`, and hence find the limiting values of `x` and `v`.  (2 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `text(See Worked Solutions)“
  3. `v -> 0, \ x -> tan^(−1)T`
Show Worked Solution

i.   `text(Newton’s 2nd law:)`

`F = mddotx = −mv(1 + v^2)`

`v · (dv)/(dx)` `= −v(1 + v^2)`
`(dv)/(dx)` `= −(1 + v^2)`
`(dx)/(dv)` `= −1/(1 + v^2)`
`x` `= −int 1/(1 + v^2)\ dv`
  `= −tan^(−1) v + C`

 

`text(When)\ \ x = 0, v = T:`

`C = tan^(−1)T`

`x = tan^(−1)T – tan^(−1)v`
 

`text(Let)\ \ x = A – B`

`A = tan^(−1) T \ => \ T = tan A`

`B = tan^(−1)v \ => \ v = tan B`

`tan x` `= tan(A – B)`
  `= (tan A – tan B)/(1 + tan A tan B)`
  `= (T – v)/(1 + Tv)`
`:. x` `= tan^(−1)((T – v)/(1 + Tv))`

 

ii.   `text(Using)\ \ ddotx = (dv)/(dt):`

`(dv)/(dt) = −1/(v(1 + v^2))`

`t = −int 1/(v(1 + v^2)) dv`
 

`text(Using Partial Fractions):`

`1/(v(1 + v^2)) = A/v + (Bv + C)/(1 + v^2)`

`A(1 + v^2) + (Bv + C)v = 1`

`A = 1`

`(A + B)v^2` `= 0`   `=> `    `B` `= −1`
`Cv` `= 0`   `=> `    `C` `= 0`

 

`t` `= −int 1/v\ dv + int v/(1 + v^2)\ dv`
  `= −log_e v + 1/2 int(2v)/(1 + v^2)\ dv`
  `= −log_e v + 1/2 log_e (1 + v^2) + C`
  `= −1/2 log_e v^2 + 1/2 log_e (1 + v^2) + C`
  `= 1/2 log_e ((1 + v^2)/(v^2)) + C`

 

`text(When)\ \ t = 0, v = T:`

`C = −1/2 log_e ((1 + T^2)/(T^2))`
 

`:. t` `= 1/2 log_e ((1 + v^2)/(v^2)) – 1/2 log_e((1 + T^2)/(T^2))`
  `= 1/2 log_e (((1 + v^2)/(v^2))/((1 + T^2)/(T^2)))`
  `= 1/2 log_e ((T^2(1 + v^2))/(v^2(1 + T^2)))`

 

iii. `t` `= 1/2 log_e ((T^2(1 + v^2))/(v^2(1 + T^2)))`
  `e^(2t)` `= (T^2(1 + v^2))/(v^2(1 + T^2))`
  `1 + v^2` `= (e^(2t)v^2(1 + T^2))/(T^2)`
  `1` `= v^2((e^(2t)(1 + T^2))/(T^2) – 1)`
  `1` `= v^2((e^(2t)(1 + T^2) – T^2)/(T^2))`
  `:. v^2` `= (T^2)/(e^(2t)(1 + T^2) – T^2)`

 
`text(As)\ \ t -> ∞:`

`v^2 -> 0, \ v -> 0`

`x = tan^(−1)T – tan^(−1)v`

`x -> tan^(−1)T`

Mechanics, EXT2 M1 EQ-Bank 1

A canon ball of mass 9 kilograms is dropped from the top of a castle at a height of `h` metres above the ground.

The canon ball experiences a resistance force due to air resistance equivalent to  `(v^2)/500`, where `v` is the speed of the canon ball in metres per second. Let  `g=9.8\ text(ms)^-2`  and the displacement, `x` metres at time `t` seconds, be measured in a downward direction.

  1. Show the equation of motion is given by
     
         `ddotx = g - (v^2)/4500`  (1 mark)

  2. Show, by integrating using partial fractions, that
     
         `v = 210((e^(7/75 t) - 1)/(e^(7/75 t) + 1))`  (5 marks)

     

  3. If the canon hits the ground after 4 seconds, calculate the height of the castle, to the nearest metre.  (3 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `text(See Worked Solutions)`
  3. `78\ text(metres)`
Show Worked Solution

i.   `text(Newton’s 2nd Law:)`

`text(Net Force)` `= mddotx`
`mddotx` `= mg – (v^2)/500`
`9ddotx` `= 9g – (v^2)/500`
`ddotx` `= g – (v^2)/4500`

 

ii.    `(dv)/(dt)` `= g – (v^2)/4500`
    `= (44\ 100 – v^2)/4500`

 
`(dt)/(dv) = 4500/(44\ 100 – v^2)`
 

`text(Using Partial Fractions:)`

`1/(44\ 100 – v^2) = A/(210- v) + B/(210 – v)`

`A(210 – v) + B(210 + v) = 1`
 

`text(If)\ \ v = 210,`

`420B = 1 \ => \ B = 1/420`
 

`text(If)\ \ v = −210,`

`420A = 1 \ => \ A = 1/420`
 

`t` `= int 4500/(210^2 – v^2)\ dv`
  `= 4500/420 int 1/(210 + v) + 1/(210 – v)\ dv`
  `= 75/7 [ln(210 + v) – ln(210 – v)] + c`
  `= 75/7 ln((210 + v)/(210 – v)) + c`

 

`text(When)\ \ t = 0, v = 0:`

`0` `= 75/7 ln(210/210) + c`
`:. c` `= 0`

 

` t` `= 75/7 ln((210 + v)/(210 – v))`
`7/75 t` `= ln((210 + v)/(210 – v))`
`e^(7/75 t)` `= (210 + v)/(210 – v)`
`e^(7/75 t) (210 – v)` `= 210 + v`
`210e^(7/75 t) – 210` `= ve^(7/75 t) + v`
`210(e^(7/75 t) – 1)` `= v(e^(7/75 t) + 1)`
`:. v` `= 210((e^(7/75 t) – 1)/(e^(7/75 t) + 1))`

 

iii.    `v · (dv)/(dx)` `= (44\ 100 – v^2)/4500`
  `(dx)/(dv)` `= (4500v)/(44\ 100 – v^2)`
  `int (dx)/(dv)\ dv` `= −4500/2 int (−2v)/(44\ 100 – v^2)\ dv`
  `x` `= −2550 log_e(44\ 100 – v^2) + c`

 
`text(When)\ \ x = 0, v = 0:`

`0` `= −2250 log_e(44\ 100) + c`
`c` `= 2250 log_e(44\ 100)`
`x` `= −2250 log_e(44\ 100 – v^2) + 2250 log_e44\ 100`
  `= 2250 log_e((44\ 100)/(44\ 100 – v^2))`

 
`text(When)\ \ t = 4:`

`v` `= 210((e^(28/75) – 1)/(e^(28/75) + 1))`
  `= 38.7509…`

 

`:. h` `= 2250 log_e((44\ 100)/(44\ 100 – 38.751^2))`
  `= 77.94…`
  `= 78\ text(metres)`

Functions, 2ADV F2 EQ-Bank 13

The curve  `y = kx^2 + c`  is subject to the following transformations

    • Translated 2 units in the positive `x`-direction
    • Dilated in the positive `y`-direction by a factor of 4
    • Reflected in the `y`-axis

The final equation of the curve is  `y = 8x^2 + 32x - 8`.

  1.  Find the equation of the graph after the dilation.  (1 mark)

  2.  Find the values of  `k`  and  `c`.  (2 marks)

Show Answers Only
  1. `y = 4k(x – 2)^2 + 4c`
  2. `k = 2, c = −10`
Show Worked Solution

i.    `y = kx^2 + c`

`text(Translate 2 units in positive)\ xtext(-direction.)`

`y = kx^2 + c \ => \ y = k(x – 2)^2 + c`

`text(Dilate in the positive)\ ytext(-direction by a factor of 4.)`

`y = k(x – 2)^2 + c \ => \ y = 4k(x – 2)^2 + 4c`

 

ii.    `y` `= 4k(x^2 – 4x + 4) + 4c`
    `= 4kx^2 – 16kx + 16k + 4c`

 

 
`text(Reflect in the)\ ytext(-axis.)`

COMMENT: Using “swap” terminology for reflections in the y-axis is simpler and more intelligible for students in our view.

`=>\ text(Swap:)\ \ x →\ – x`

`y` `= 4k(−x)^2 – 16k(−x) + 16k + 4c`
  `= 4kx^2 + 16kx + 16k + 4c`

 

 
`text(Equating co-efficients:)`

`4k` `=8`  
`:. k` `=2`  

 

`16k + 4c` `= −8`
`4c` `= −40`
`:. c` `=-10`

Trigonometry, 2ADV T3 EQ-Bank 3

By drawing graphs on the number plane, show how many solutions exist for the equation  `cosx = |(x - pi)/4|`  in the domain  `(−∞, ∞)`  (3 marks)

Show Answers Only

`text(4 solutions)`

Show Worked Solution

`text(Sketch:)`

`y` `= cos x`
`y` `= |(x – pi)/4|`

 
`text(Translate)\ pi\ text(units to the right: )`

`y=|x| \ => \ y=|x-pi|`

`text(Multiply by)\ 1/4 :`

`y=|x-pi| \ => \ y= 1/4 |x-pi| = |(x-pi)/4|`

`:.\ text(There are 4 solutions.)`

Calculus, 2ADV C4 EQ-Bank 5

The velocity of a particle moving along the `x`-axis at `v` metres per second at `t` seconds, is shown in the graph below.
 


 

Initially, the displacement `x` is equal to 12 metres.

  1. Write an equation that describes the displacement, `x`, at time `t` seconds.  (2 marks)

  2. Draw a graph that shows the displacement of the particle, `x`  metres from the origin, at a time `t` seconds between  `t= 0`  and  `t = 5`. Label the coordinates of the endpoints of your graph.  (2 marks)

Show Answers Only
  1. `x = 3t – (3)/(10) t ^2 + 12`
  2.  

Show Worked Solution
i.    `m_v` `= -(3)/(5)`
  `v` `= 3 – (3)/(5) t`

 

`x` `= int v \ dt`
  `= int 3 – (3)/(5) t \ dt`
  `= 3t – (3)/(10) t^2 + c`

 
`text(When) \ \ t = 0, x = 12  \ => \ c = 12`

`:. \ x = 3t – (3)/(10) t ^2 + 12`

 

ii.  `text(When) \ \ t = 5:`

`x = 15 – (3)/(10) xx 25 + 12 = 19.5`
 

Statistics, 2ADV S3 EQ-Bank 1

A probability density function can be used to model the lifespan of a termite, `X`, in weeks, is given by
 

`f(x) = {(k(36 - x^2)),(0):}\ \ \ {:(3 <= x <= 6),(text(otherwise)):}`
 

  1. Show that the value of  `k`  is  `1/45`.  (2 marks)

  2. Find the cumulative distribution function.  (2 marks)

  3. Find the probability that a termite's lifespan is greater than 5 weeks.  (1 mark)

Show Answers Only
  1. `text(See Worked Solutions)`
  2. `F(x) = {(0),(1/135 (108t – t^3  – 297)),(1):}\ \ \ {:(x < 3),(3 <= x <= 6),(x > 6):}`
  3. `17/135`
Show Worked Solution
i.    `k int_3^6 36 – x^2\ dx` `= 1`
  `k[36x – (x^3)/3]_3^6` `= 1`
  `k[(216 – 72)-(108 – 9)]` `= 1`
  `45k` `= 1`
  `k` `= 1/45`

 

ii.    `F(t)` `= int_(-∞)^t f(x)\ dx`
    `= int_3^t f(x)\ dx`
    `= 1/45 int_3^t 36 – x^2\ dx`
    `= 1/45 [36x – (x^3)/3]_3^t`
    `= 1/135[108x – x^3]_3^t`
    `= 1/35[(108t – t^3) – (324 – 27)]`
    `= 1/135(108t – t^3 – 297)`

 
`:. F(x) = {(0),(1/135 (108t – t^3  – 297)),(1):}\ \ \ {:(x < 3),(3 <= x <= 6),(x > 6):}`

 

iii.    `P(X > 5)` `= 1 – F(5)`
    `= 1 – 1/135(108 xx 5 – 5^3 – 297)`
    `= 1 – 118/135`
    `= 17/135`

NETWORKS, FUR2-NHT 2019 VCAA 3

The zoo’s management requests quotes for parts of the new building works.

Four businesses each submit quotes for four different tasks.

Each business will be offered only one task.

The quoted cost, in $100 000, of providing the work is shown in Table 1 below.
  


 

The zoo’s management wants to complete the new building works at minimum cost.

The Hungarian algorithm is used to determine the allocation of tasks to businesses.

The first step of the Hungarian algorithm involves row reduction; that is, subtracting the smallest element in each row of Table 1 from each of the elements in that row.

The result of the first step is shown in Table 2 below.
 


 

The second step of the Hungarian algorithm involves column reduction; that is, subtracting the smallest element in each column of Table 2 from each of the elements in that column.

The results of the second step of the Hungarian algorithm are shown in Table 3 below. The values of Task 1 are given as `A, B, C` and `D`.
 


 

  1. Write down the values of `A, B, C` and `D`.   (1 mark)

  2. The next step of the Hungarian algorithm involves covering all the zero elements with horizontal or vertical lines. The minimum number of lines required to cover the zeros is three.

     

    Draw these three lines on Table 3 above.   (1 mark)

  3. An allocation for minimum cost is not yet possible.

     

    When all steps of the Hungarian algorithm are complete, a bipartite graph can show the allocation for minimum cost.

     

    Complete the bipartite graph below to show this allocation for minimum cost.   (1 mark)

     

  1. Business 4 has changed its quote for the construction of the pathways. The new cost is $1 000 000. The overall minimum cost of the building works is now reduced by reallocating the tasks.

     

    How much is this reduction?   (1 mark)

Show Answers Only
  1. `A = 2, B = 1, C = 1, D = 0`
  2. `text(See Worked Solutions)`
  3. `text(See Worked Solutions)`
  4. `text(See Worked Solutions)`
Show Worked Solution

a.   `A = 2, \ B = 1, \ C = 1, \ D = 0`

 

b.  

 

c.  `text(After next step:)`
 

`text(Allocation): `
 

 

d.  `text{Hungarian Algorithm table (complete):}`
 

`text(Allocation): B2 -> T3,\ B1 -> T4,\ B3 -> T2,\ B4 -> T1`
 

`text(C)text(ost) = 4 + 7 + 8 + 10 = 29`

`text(Previous cost) = 5 + 10 + 8 + 8 = 31`
 

`:.\ text(Reduction)` `= 2 xx 100\ 000`
  `= $200\ 000`

Financial Maths, GEN1 2019 NHT 22-23 MC

Armand borrowed $12 000 to pay for a holiday.

He will be charged interest at the rate of 6.12% per annum, compounding monthly.

This loan will be repaid with monthly repayments of $500.
 

Part 1

After four months, the total interest that Armand will have paid is closest to

  1.   $231
  2.   $245
  3.   $255
  4.   $734
  5. $1796

 
Part 2

After eight repayments, Armand decided to increase the value of his monthly repayments.

He will make a number of monthly repayments of $850 and then one final repayment that will have a smaller value.

This final repayment has a value closest to

  1. $168
  2. $169
  3. $180
  4. $586
  5. $681
Show Answers Only

`text(Part 1:)\ A`

`text(Part 2:)\ B`

Show Worked Solution

`text(Part 1)`

`text(By TVM Solver:)`

`N` `= 4`
`Itext(%)` `= 6.12`
`PV` `= 12\ 000`
`PMT` `= −500`
`FV` `= ?`
`text(P/Y)` `= text(C/Y) = 12`

 
`=>\ text(FV) = 10\ 231.33`

`:.\ text(Total interest)` `=\ text(total payments − reduction in principle)`
  `= (4 xx 500) – (12\ 000 – 10\ 231.33)`
  `= 231.33`

`=>\ A`

 

`text(Part 2)`

`text(Loan after 8 repayments (by TVM Solver)):`

`N` `= 8`
`I(text(%))` `= 6.12`
`PV` `= 12\ 000`
`PMT` `= −500`
`FV` `= ?`
`text(P/Y)` `= text(C/Y) = 12`

 

 
`=> FV = 8426.30`

 

`text(Number of repayments required at $850)`

`N` `= ?`
`I(text(%))` `= 6.12`
`PV` `= 8426.30`
`PMT` `= −500`
`FV` `= 0`
`text(P/Y)` `= 12`
`text(C/Y)` `= 12`

 
`=> N = 10.2`

 
`text(Balance after 10 repayments = $168.29)`

`:.\ text(Final repayment)` `= 168.29 xx (1 + 6.12/12)`
  `= 169.15`

`=>\ B`

GEOMETRY, FUR1-NHT 2019 VCAA 7 MC

Two similar right-angled triangles are shown in the diagram below.
 

     

The total perimeter of the two triangles, in metres, is

  1. 21
  2. 30
  3. 36
  4. 42
  5. 45
Show Answers Only

`C`

Show Worked Solution

     

`text(Ratio of similar sides)\ = 3 : 6 = 1 : 2`

`text(Base of 12 m in ratio)\ 1 : 2 = 4 : 8`

 
 

`text(Length of hypotenuses:)`

`h_1 = sqrt(3^2 + 4^2) = 5`

`h_2 = sqrt(6^2 + 8^2) = 10`
 

`:. \ text(Perimeter) ` `= 3 + 4 + 5 + 6 + 8 + 10`
  `= 36 \ text(m)`

 
`=> \ C`

GEOMETRY, FUR1-NHT 2019 VCAA 4 MC

A pizza in the shape of a circle has been cut into 12 equal slices.

The area of the top surfaces of one slice is 9.42 cm2, as shown shaded in the diagram below.
  

     
 

The perimeter of the top surfaces of one slice of pizza, in centimetres, is closest to

  1.   9.14
  2. 15.14
  3. 18.00
  4. 21.99
  5. 40.84
Show Answers Only

`B`

Show Worked Solution
`text(Total Area)` `= 12 xx 9.42`
  `= 113.04 \ text(cm)^2`

 

`pi r^2` `= 113.04`
`r` `= sqrt({113.04}/{pi})`
  `= 5.998 \ …`
  `≈ 6`

 
`:. \ text(Perimeter of 1 slice)`

`= 2 xx 6 + (1)/(12) (2 xx pi xx 6)`

`= 15.14 \ text(cm)`
 

`=> \ B`

MATRICES, FUR2-NHT 2019 VCAA 4

After 5.00 pm, tourists will start to arrive in Gillen and they will stay overnight.

As a result, the number of people in Gillen will increase and the television viewing habits of the tourists will also be monitored.

Assume that 50 tourists arrive every hour.

It is expected that 80% of arriving tourists will watch only `C_2` during the hour that they arrive.

The remaining 20% of arriving tourists will not watch television during the hour that they arrive.

Let `W_m` be the state matrix that shows the number of people in each category `m` hours after 5.00 pm on this day.

The recurrence relation that models the change in the television viewing habits of this increasing number of people in Gillen `m` hours after 5.00 pm on this day is shown below.

`W_(m + 1) = TW_m + V` 

where

`{:(quad qquad qquad qquadqquadqquadquadtext(this hour)),(qquadqquadqquad quad \ C_1 qquad quad C_2 qquad \ C_3 quad \ NoTV),(T = [(quad 0.50, 0.05, 0.10, 0.20 quad),(quad 0.10, 0.60, 0.20, 0.20 quad),(quad 0.25, 0.10, 0.50, 0.10 quad),(quad 0.15, 0.25, 0.20, 0.50 quad)]{:(C_1),(C_2),(C_3),(NoTV):}\ text(next hour,) qquad and qquad  W_0 = [(400), (600), (300),(700)]):}`
 

  1. Write down matrix `V`.   (1 mark)

  2. How many people in Gillen are expected to watch `C_2` at 7.00 pm on this day?   (2 marks)

Show Answers Only
  1.  `V=[(0),(40),(0),(10)]`
  2.  `666`
Show Worked Solution

a.   `V=[(0),(40),(0),(10)]`

b.    `W_1` `=TW_0+V`
    `=[(quad 0.50, 0.05, 0.10, 0.20 quad),(quad 0.10, 0.60, 0.20, 0.20 quad),(quad 0.25, 0.10, 0.50, 0.10 quad),(quad 0.15, 0.25, 0.20, 0.50 quad)] [(400),(600),(300),(700)]+[(0),(40),(0),(10)]=[(400),(640),(380),(630)]`
     
  `W_2` `=TW_1+V=[(396),(666),(417),(621)]`

 
`:.\ text(666 people are expected to watch)\ C_2\ text(at 7 pm.)`

L&E, 2ADV E1 2019 NHT 4

Solve  `log_3(t)-log_3(t^2-4) = -1`  for  `t`.   (3 marks)

Show Answers Only

`4 `

Show Worked Solution
`log_3(t)-log_3(t^2-4)` `= -1`
`log_3 ({t}/{t^2-4})` `= -1`
`(t)/(t^2-4)` `= (1)/(3)`
`t^2-4` `= 3t`
`t^2-3t-4` `= 0`
`(t-4)(t+ 1)` `= 0`

 
`:. t=4 \ \ \ (t > 0, \ t!= –1)`

Calculus, MET1-NHT 2018 VCAA 9

Let diagram below shows a trapezium with vertices at  `(0, 0), (0, 2), (3, 2)`  and  `(b, 0)`, where  `b`  is a real number and  `0 < b < 2`

On the same axes as the trapezium, part of the graph of a cubic polynomial function is drawn. It has the rule  `y = ax(x-b)^2`, where  `a`  is a non-zero real number and  `0 ≤ x ≤ b`.

  1. At the local maximum of the graph, `y = b`.
  2. Find `a` in terms of `b`.   (3 marks)

The area between the graph of the function and the `x`-axis is removed from the trapezium, as shown in the diagram.
 

  1. Show that the expression for the area of the shaded region is  `b + 3-(9b^2)/(16)`  square units.   (3 marks)

  2. Find the value of  `b`  for which the area of the shaded region is a maximum and find this maximum area.   (2 marks)

Show Answers Only
  1. `(27)/(4b^2)`
  2. `text(Proof (See Worked Solution))`
  3. `(31)/(9)`
Show Worked Solution
a.     `y` `= ax(x-b)^2`
`y^{′}` `= a(x-b)^2 + 2ax(x-b)`
  `= a(x-b)(x-b + 2x)`
  `= a(x-b)(3x-b)`

 
`text(S) text(olve) \ \ y^{′} = 0 \ \ text(for) \ x:`

`x = b \ \ text(or) \ \ (b)/(3)`
 
`y_text(max) = b \ \ text{(given) and occurs at} \ \ x = (b)/(3)`
 

`b` `= a((b)/(3))((b)/(3)-b)^2`
`b` `= a((b)/(3))((4b^2)/(9))`
`b` `= a((4b^3)/(27))`

 
`:. \ a = (27)/(4b^2)`
 

b.   `text(Let)\ \ A_1 = \ text(area under the graph)`

`A_1` `= int_0^b ax (x-b)^2 dx`
  `= a int_0^b x(x^2-2bx + b^2)\ dx`
  `= (27)/(4b^2) int_0^b x^3-2bx^2 + b^2 x \ dx`
  `= (27)/(4b^2) [(x^4)/(4)-(2bx^3)/(3) + (b^2 x^2)/(2)]_0^b`
  `= (27)/(4b^2) ((b^4)/(4)-(2b^4)/(3) + (b^4)/(2))`
  `= (27)/(4b^2) ((b^4)/(12))`
  `= (9b^2)/(16)`

 
`text(Let) \ \ A_2 = \ text(area of triangle)`

`A_2 = (1)/(2) xx 2 xx (3-b) = 3-b`
 

`:. \ text(Shaded region)` `= 6-(9b^2)/(16)-(3-b)`
  `= b + 3-(9b^2)/(16)`

 

c.   `A = b + 3-(9b^2)/(16)`

`(dA)/(db) = 1-(9b)/(8)`

`(dA^2)/(db^2) =-(9)/(8) <0`
 

`=>\ text{SP (max) when} \ \ (dA)/(db) = 0`

`(9b)/(8) = 1 \ => \ \ b = (8)/(9)`

`:. A_(max)` `= (8)/(9) + 3-{9((8)/(9))^2}/{16}`
  `= (35)/(9)-(64)/(9 xx 16)`
  `= (31)/(9)`

Statistics, MET1-NHT 2018 VCAA 8

Let  `overset^p`  be the random variable that represents the sample proportions of customers who bring their own shopping bags to a large shopping centre.

From a sample consisting of all customers on a particular day, an approximate 95% confidence interval for the proportion  `p`  of customers who bring their own shopping bags to this large shopping centre was determined to be  `((4853)/(50\ 000) , (5147)/(50\ 000))`.

  1. Find the value of  `hatp`  that was used to obtain this approximate 95% confidence interval.   (1 mark)

  2. Use the fact that  `1.96 = (49)/(25)`  to find the size of the sample from which this approximate 95% confidence interval was obtained.   (2 marks)

Show Answers Only

  1. `(1)/(10)`
  2. `40\ 000`

Show Worked Solution

a.    `overset^p – z sqrt((overset^p(1 – overset^p))/(n)) = (4853)/(50\ 000) \ \ , \ \ overset^p + z sqrt((overset^p(1 – overset^p))/(n)) = (5147)/(50\ 000)`

`2 overset^p` `= (4853)/(50\ 000) + (5147)/(50\ 000)`  
`:. \ overset^p` `=1/10`  

 

b.    `(1)/(10) + (49)/(25) sqrt(({1)/{10}(1 – {1}/{10}))/(n)` `= (5147)/(50000)`
`(49)/(25) sqrt((9)/(100n))` `= (147)/(50000)`
`(49)/(25) * (3)/(10) * (1)/(sqrtn)` `= (147)/(25 xx 2000)`
`(147)/(sqrtn)` `= (147)/(200)`
`sqrtn` `= 200`
`:. \ n` `= 40\ 000`

Statistics, MET1-NHT 2018 VCAA 6

The discrete random variable `X` has the probability mass function
 

`text(Pr)(X = x) = {(kx), (k), (0):} qquad {:(x∈{1, 4, 6}), (x = 3), (text(otherwise)):}`
 

  1. Show that  `k = (1)/(12)`.  (2 marks)

  2. Find  `text(E)(X)`.  (1 mark)

  3. Evaluate  `text(Pr)(X ≥ 3 | X ≥ 2)`.  (1 mark)

Show Answers Only

  1. `text(Proof (See Worked Solution))`
  2. `(14)/(3)`
  3. `1`

Show Worked Solution

a.     `qquad X` `qquad 1 qquad` `qquad 3 qquad` `qquad 4 qquad` `qquad 6 qquad`
  `qquad Pr(X = x) qquad` `k` `k` `4k` `6k`

 

`k + k+4k + 6k` `= 1`
`12k` `= 1`
`k` `= (1)/(12)`

 

b.    `E(X)` `= ∑ x text(Pr)(X = x)`
  `= k + 3k + 16k + 36k`
  `= 56k`
  `= (56)/(12)`
  `= (14)/(3)`

 

c.    `text(Pr) (X ≥ 3 | X ≥ 2)` `= (text(Pr) (X ≥ 3 ∩ X ≥ 2))/(text(Pr) (X ≥ 2))`
  `= (text(Pr) (X ≥ 3))/(text(Pr) (X ≥ 2))`
  `= (k + 4k + 6k)/(k + 4k + 6k)`
  `= 1`

Financial Maths, GEN1 2019 NHT 21 MC

Yazhen has a reducing balance loan.

Six lines of the amortisation table for Yazhen’s loan are shown below.

The interest rate for Yazhen’s loan increased after one of these six repayments had been made.

The first repayment made at the higher interest rate was repayment number

  1. 15
  2. 16
  3. 17
  4. 18
  5. 19
Show Answers Only

`C`

Show Worked Solution

`text(Interest rate) = text(Interest)/text{Balance (higher row)}`
 

`text(Payment 16:)\ \ \ 343/(34\ 299.50) = 0.0100`

`text(Payment 17:)\ \ \ 403.71/(33\ 642.50) = 0.0120`

`text(Payment 18:)\ \ \ 396.55/(33\ 046.21) = 0.0120`
 

`:.\ text(Payment 17 is the 1st at the higher rate.)`

`=>\ C`

Statistics, EXT1 S1 EQ-Bank 14

It is known that 65% of adults over the age of 60 have been tested for bowel cancer.

A random sample of 140 adults aged over 60 years is surveyed.

Using a normal approximation to the binomial distribution and the probability table attached, calculate the probability that at least 85 of the adults chosen have been tested for bowel cancer.   (3 marks)

Show Answers Only

`0.8554`

Show Worked Solution

`text(Let)\ \ X =\ text(number tested for cancer)`

`X\ ~\ text(Bin)(140, 0.65)`

`text(Find)\ \ P(X>=85):`

`E(hat p)` `=p=0.65`  
`text(Var)(hat p)` ` = (0.65(0.35))/140 = 0.001625`  
`sigma(hat p)` `=0.04031…`  

 
`hatp\ ~\ N(mu,sigma)\ ~\ N(0.65, 0.04031…)`

`text(If)\ \ X=85\ \ => \ hatp=85/140=0.60714…`

`ztext{-score}\ (X=85)` `=(0.60714-0.65)/0.04031`  
  `~~ -1.063`  

 
`text{Using the probability table (attached):}`

`P(z<–1.06) = 0.1446`

`:. P(X>=85)` `=1-0.1446`  
  `=0.8554`  

Financial Maths, GEN2 2019 NHT 8

A record producer gave the band $50 000 to write and record an album of songs.

This $50 000 was invested in an annuity that provides a monthly payment to the band.

The annuity pays interest at the rate of 3.12% per annum, compounding monthly.

After six months of writing and recording, the band has $32 667.68 remaining in the annuity.

  1. What is the value, in dollars, of the monthly payment to the band?   (1 mark)

  2. After six months of writing and recording, the band decided that it needs more time to finish the album.

     

    To extend the time that the annuity will last, the band will work for three more months without withdrawing a payment.

     

    After this, the band will receive monthly payments of $3800 for as long as possible.

     

    The annuity will end with one final monthly payment that will be smaller than all of the others.

     

    Calculate the total number of months that this annuity will last.   (2 marks)

Show Answers Only
  1. `$3000`
  2. `18`
Show Worked Solution

a.    `text(By TVM Solver:)`

`N` `= 6`  
`I text(%)` `=3.12`  
`PV` `=50\ 000`  
`PMT` `= ?`  
`FV` `=-32\ 667.68`  
`text(PY)` `= text(CY) = 12`  

 
`=> PMT = -3000.00`

`:. \ text(Monthly payment) = $3000`

 

b.   `text{Value after 3 more months (by TVM Solver):}`

`N` `= 3`  
`I text(%)` `=3.12`  
`PV` `=32\ 667.68`  
`PMT` `= 0`  
`FV` `=?`  
`text(PY)` `= text(CY) = 12`  

 
`=> FV = -32\ 923.15`
 

`text(Find) \ \ N \ text(when) \ FV= 0 \ text{(by TVM Solver):}`

`N` `= ?`  
`I text(%)` `=3.12`  
`PV` `=-32\ 923.15`  
`PMT` `= 3800`  
`FV` `=0`  
`text(PY)` `= text(CY) = 12`  

 
`=> N = 8.77`

`:. \ text(Total months of annuity)` `= 6 + 3 + 9`
  `= 18`

Financial Maths, GEN2 2019 NHT 7

Tisha plays drums in the same band as Marlon.

She would like to buy a new drum kit and has saved $2500.

  1. Tisha could invest this money in an account that pays interest compounding monthly.

     

    The balance of this investment after `n` months, `T_n` could be determined using the recurrence relation below
     
          `T_0 = 2500, \ \ \ \ T_(n+1) = 1.0036 xx T_n` 
     
    Calculate the total interest that would be earned by Tisha's investment in the first five months.

     

    Round your answer to the nearest cent.   (2 marks)

Tisha could invest the $2500 in a different account that pays interest at the rate of 4.08% per annum, compounding monthly. She would make a payment of $150 into this account every month.

  1. Let `V_n` be the value of Tisha's investment after `n` months.

     

    Write down a recurrence relation, in terms of `V_0`, `V_n` and `V_(n + 1)`, that would model the change in the value of this investment.   (1 mark)

  2. Tisha would like to have a balance of $4500, to the nearest dollar, after 12 months.

     

    What annual interest rate would Tisha require?

     

    Round your answer to two decimal places.   (1 mark)

Show Answers Only
  1. `$45.33`
  2. `V_0 = 2500, \ V_(n+1) = 1.0034 xx V_n + 150`
  3. `5.87%`
Show Worked Solution

a.    `T_1 = 1.0036 xx 2500 = 2509`

`T_2 = 1.0036 xx 2509 = 2518.0324`

`vdots`

`T_5 = 2545.33`

`:. \ text(Total interest) ` `= 2545.33-2500`
  `= $45.33`

 

b.    `text(Monthly interest) = (4.08)/(12) = 0.34%`

`:. \ V_0 = 2500, \ V_(n+1) = 1.0034 xx V_n + 150`

 

c.    `text(By TVM Solver:)`

`N` `= 12`  
`I text(%)` `=?`  
`PV` `=-2500`  
`PMT` `=-150`  
`FV` `=4500`  
`text(PY)` `= text(CY)=12`  

 
`=> I = 5.87%`

Data Analysis, GEN2 2019 NHT 5

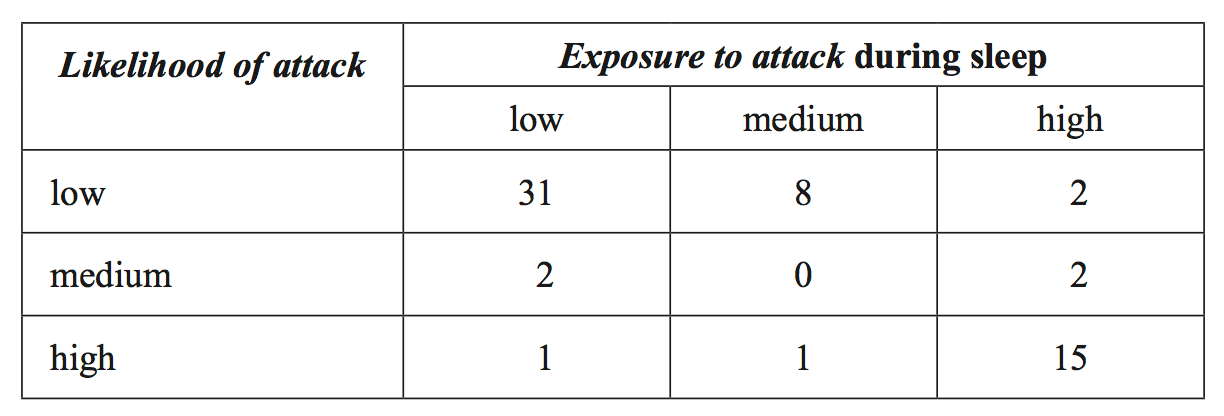
A random sample of 12 mammals drawn from a population of 62 types of mammals was categorized according to two variables.

likelihood of attack (1 = low, 2 = medium, 3 = high)

exposure to attack during sleep (1 = low, 2 = medium, 3 = high)

The data is shown in the following table.
 


 

  1. Use this data to complete the two-way frequency table below.   (1 mark)

      
         
     

The following two-way frequency table was formed from the data generated when the entire population of 62 types of mammals was similarly categorized.
 
     

    1. How many of these 62 mammals had both a high likelihood of attack and a high exposure to attack during sleep?   (1 mark)

    2. Of those mammals that had a medium likelihood of attack, what percentage also had a low exposure to attack during sleep?   (1 mark)

    3. Does the information in the table above support the contention that likelihood of attack is associated with exposure to attack during sleep? justify your answer by quoting appropriate percentages. It is sufficient to consider only one category of likelihood of attack when justifying your answer.   (2 marks)

Show Answers Only

  1.  
    1. `15`
    2. `text(Percentage) = (2)/(4) xx 100`
                           `= 50 %`
    3. `text(The data supports the contention that animals with a low likelihood)`
      `text(of attack is associated with low exposure to attack during sleep.)`
       
      `text(- 91%) \ ({31}/{34}) \ text(of animals with low exposure to attack)`
         `text(during sleep, have a low likelihood of attack.)`
       
      `text(- Similarly, 89% of animals with a medium exposure to attack during)`
         `text(sleep have a low likelihood of attack.)`
       
      `text(- 11% of animals with a high exposure to attack during sleep have)`
          `text(a low likelihood of attack)`

Show Worked Solution

a.     

 

b.    i. `15`

ii.   `text(Percentage)` `= (2)/(4) xx 100`
  `= 50%`

 

iii. `text(The data supports the contention that animals with a low likelihood)`

`text(of attack is associated with low exposure to attack during sleep.)`

`text(- 91%) \ ({31}/{34}) \ text(of animals with low exposure to attack)`

`text(during sleep, have a low likelihood of attack.)`

`text(- Similarly, 89% of animals with a medium exposure to attack during)`

`text(sleep have a low likelihood of attack.)`

`text(- 11% of animals with a high exposure to attack during sleep have)`

`text(a low likelihood of attack)`

Data Analysis, GEN2 2019 NHT 4

The scatterplot below plots the variable life span, in years, against the variable sleep time, in hours, for a sample of 19 types of mammals.
 

On the assumption that the association between sleep time and life span is linear, a least squares line is fitted to this data with sleep time as the explanatory variable.

The equation of this least squares line is

life span = 42.1 – 1.90 × sleep time

The coefficient of determination is 0.416

  1. Draw the graph of the least squares line on the scatterplot above.   (1 mark)

  2. Describe the linear association between life span and sleep time in terms of strength and direction.   (2 marks)

  3. Interpret the slope of the least squares line in terms of life span and sleep time.   (2 marks)

  4. Interpret the coefficient of determination in terms of life span and sleep time.   (1 mark)

  5. The life of the mammal with a sleep time of 12 hours is 39.2 years.
  6. Show that, when the least squares line is used to predict the life span of this mammal, the residual is 19.9 years.   (2 marks)

Show Answers Only
  1.  

  2. `text(Strength is moderate.)`

     

    `text(Direction is negative.)`

  3. `text(The gradient of –1.9 means that life span decreases by)` 

     

    `text(1.9 years for each additional hour of sleep time.)`

  4. `text(41.6% of the variation in life span can be explained by the)`

     

    `text(variation in sleep time.)`

  5. `text(Proof(See Worked Solution))`
Show Worked Solution

a.    `text{Graph endpoints (0, 42.1) and (18, 7.9)}`
 


 

b.   `text(Strength is moderate.)`

`text(Direction is negative.)`
 

c.    `text(The gradient of –1.9 means that life span decreases by)`

`text(1.9 years for each additional hour of sleep time.)`

 

d.    `text(41.6% of the variation in life span can be explained by the )`

`text(variation in sleep time.)`
 

e.    `text(Predicted value)` `= 42.1 – 1.9 xx 12`
  `= 19.3 \ text(years)`

 

`text(Residual)` `= text(actual) – text(predicted)`
  `= 39.2 – 19.3`
  `= 19.9 \ text(years)`

MATRICES, FUR1-NHT 2019 VCAA 7-8 MC

A farm contains four water sources, `P`, `Q`, `R` and `S`.

Part 1

Cows on the farm are free to move between the four water sources.

The change in the number of cows at each of these water sources from week to week is shown in the transition diagram below.
 

Let `C_n` be the state matrix for the location of the cows in week `n` of 2019.

The state matrix for the location of the cows in week 23 of 2019 is `C_23 = [(180),(200),(240),(180)]{:(P),(Q),(R),(S):}`
 

The state matrix for the location of the cows in week 24 of 2019 is `C_24 = [(160),(222),(203),(215)]{:(P),(Q),(R),(S):}`

Of the cows expected to be at `Q` in week 24 of 2019, the percentage of these cows at `R` in week 23 of 2019 is closest to

  1.   8%
  2.   9%
  3. 20%
  4. 22%
  5. 25%

 

Part 2

Sheep on the farm are also free to move between the four water sources.

The change in the number of sheep at each water source from week to week is shown in matrix `T` below.
 

`{:(),(),(T=):}{:(qquadqquadqquadtext(this week)),((qquadP,quadQ,quadR,quadS)),([(0.4,0.3,0.2,0.1),(0.2,0.1,0.5,0.3),(0.1,0.3,0.1,0.2),(0.3,0.3,0.2,0.4)]):}{:(),(),({:(P),(Q),(R),(S):}):}{:(),(),(text(next week)):}`
 

In the long term, 635 sheep are expected to be at `S` each week.

In the long term, the number of sheep expected to be at `Q` each week is closest to

  1. 371
  2. 493
  3. 527
  4. 607
  5. 635
Show Answers Only

`text(Part 1:)\ D`

`text(Part 2:)\ C`

Show Worked Solution

`text(Part 1)`

`text(In week 23, 240 cows are at)\ R.`

`text(In week 24, number of cows moving from)\ R\ text(to)\ Q`

`=20text(%) xx 240`

`= 48\ text(cows)`
 

`text(Total cows at)\ Q = 222`
 

`:.\ text(Percentage)` `= 48/222`
  `= 0.2162`
  `= 22text(%)`

`=>\ D`

 

`text(Part 2)`

`T^50 = [(0.2434, 0.2434, 0.2434, 0.2434),(0.2603, 0.2603, 0.2603, 0.2603),(0.1834, 0.1834, 0.1834, 0.1834),(0.3130, 0.3130, 0.3130, 0.3130)]`

 
`text(S)text(ince 635 sheep are expected long term at)\ S,`

`text(Total sheep)` `= 635/0.3130`
  `= 2029`

 
`:. text(Long term expected at)\ Q`

`~~ 0.2603 xx 2029`

`~~ 528`

`=>\ C`

GRAPHS, FUR1-NHT 2019 VCAA 7 MC

The shaded area in the graph below represents the feasible region for a linear programming problem.
 


 

The maximum value of the objective function  `Z = -2x - 2y` occurs at

  1. point `C` only.
  2. any point along line segment  `BC`.
  3. any point along line segment  `AD`.
  4. any point along line segment  `AB`.
  5. any point along line segment  `DC`.
Show Answers Only

`C`

Show Worked Solution

`text(Equation of)\ \ BC \ => \ x + y = 10`

`text(Equation of)\ \ AD \ => \ x + y = 5`

`Z` `= -2x – 2y`
  `= -2(x + y)`

 
`text(Along)\ \ AD,\ Z = -10`

`text(Along)\ \ BC,\ Z = -20`

`:.\ text(Max value of)\ \ Z = -10`
 

`=>  C`

GRAPHS, FUR1-NHT 2019 VCAA 4 MC

A farm has `x` cows and `y` sheep.

On this farm there are always at least twice as many sheep as cows.

The relationship between the number of cows and the number of sheep on this farm can be represented by the inequality

  1.  `x <= y/2`
  2.  `y <= x/2`
  3.  `2x >= y`
  4.  `2y >= x`
  5.  `xy >= 2`
Show Answers Only

`A`

Show Worked Solution

`text(If twice as many sheep as cows)`

`y = 2x`

`text(If at least twice as many sheep as cows)`

`y` `>= 2x`
`x` `<= y/2`

 
`=>  A`

MATRICES, FUR1-NHT 2019 VCAA 5 MC

A population of birds feeds at two different locations, `A` and `B`, on an island.

The change in the percentage of the birds at each location from year to year can be determined from the transition matrix `T` shown below.
 

`{:(),(),(T=):}{:(qquadtext(this year)),((qquadA,\ B)),([(0.8,0.4),(0.2,0.6)]):}{:(),(),({:(A),(B):}):}{:(),(),(text(next year)):}`
 

In 2018, 55% of the birds fed at location `B`.

In 2019, the percentage of the birds that are expected to feed at location `A` is

  1. 32%
  2. 42%
  3. 48%
  4. 58%
  5. 62%
Show Answers Only

`D`

Show Worked Solution

`[(A_2019),(B_2019)] = [(0.8,0.4),(0.2,0.6)][(0.45),(0.55)] = [(0.58),(0.42)]`

`=>\ D`

NETWORKS, FUR1-NHT 2019 VCAA 7 MC

A graph has five vertices, `A, B, C, D` and `E`.

The adjacency matrix for this graph is shown below.
 

`{:(qquad qquad A quad B quad C quad D quad E), ({:(A), (B), (C), (D), (E):} [(0, 1, 0, 1, 2),(1, 0, 1, 0, 1),(0, 1, 1, 0, 1),(1, 0, 0, 0, 1),(2, 1, 1, 1, 0)]):}`
 

Which one of the following statements about this graph is not true?

  1. The graph is connected.
  2. The graph contains an Eulerian trail.
  3. The graph contains an Eulerian circuit.
  4. The graph contains a Hamiltonian cycle.
  5. The graph contains a loop and multiple edges.
Show Answers Only

`C`

Show Worked Solution

`text(Consider the degree of each vertex:)`

`A – 4, B – 3, C – 3, D – 2, E – 5`

`text{Graph cannot be an Eulerian circuit because it}`

`text{has odd degree vertices.}`

`text{Note that an Eulerian circuit cannot have an odd degree}`

`text{vertex as it uses all edges exactly once and begins and ends}`

`text{at the same vertex.}`

`=>  C`