SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

ENGINEERING, CS 2021 HSC 17 MC

Which of the following is a specialised test used to determine the compressive strength of cured concrete?

  1. Slump test
  2. Janka hardness test
  3. Shore hardness test
  4. Rebound hammer test
Show Answers Only

`D`

Show Worked Solution

Considering each option:

  • Slump test – tests the workability and consistency of wet concrete.
  • Janka hardness test – tests hardwood flooring.
  • Shore hardness test – tests soft elastomers and other soft polymers.
  • Rebound hammer test – tests the compressive strength of cured concrete.

`=>D`

♦♦♦ Mean mark 19%.

ENGINEERING, TE 2021 HSC 15 MC

Which of the following would be the most suitable material to use for a spring in a telecommunication component?

  1. Annealed copper zinc alloy
  2. Electrolytic tough pitch copper
  3. Age hardened aluminium silicon alloy
  4. Age hardened copper–beryllium alloy
Show Answers Only

`D`

Show Worked Solution
  • Age hardened copper-beryllium alloy is used due to its conductivity, low sparking capabilities and physical capabilities of hardness and strength in high temperature conditions.

`=>D`

♦♦♦ Mean mark 29%.

BIOLOGY, M5 2020 HSC 19 MC

Which diagram correctly models one phase of meiosis in an organism that has six chromosomes in its somatic cells?

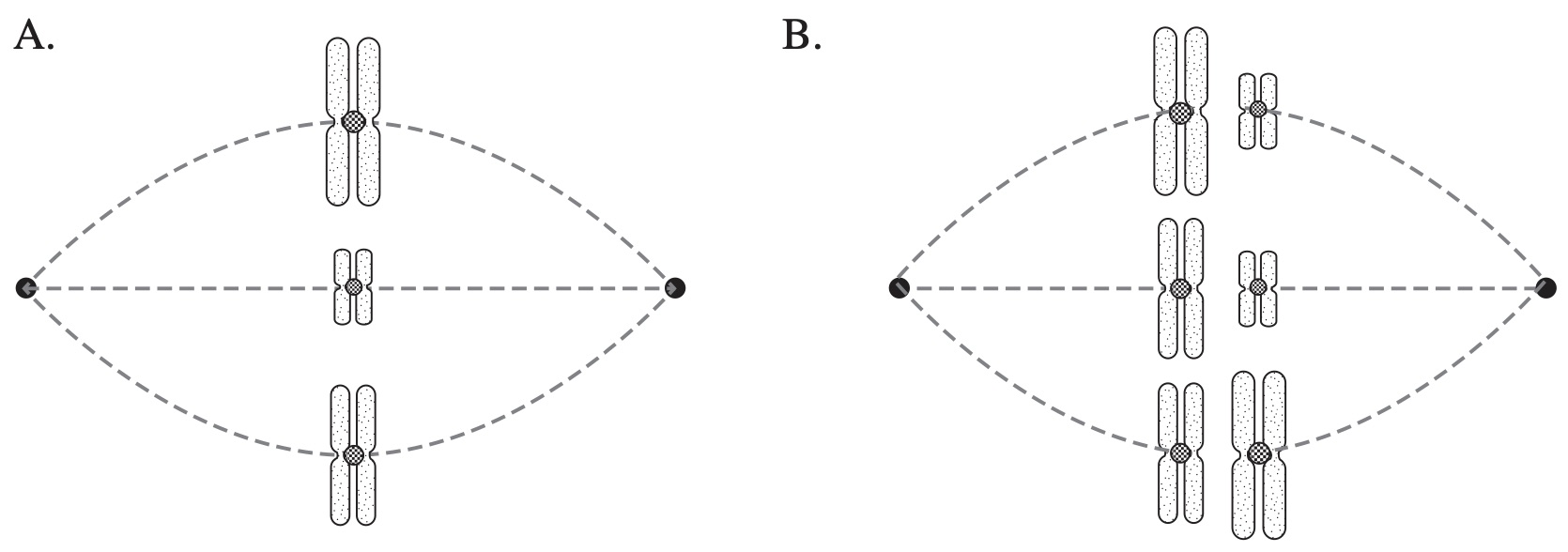
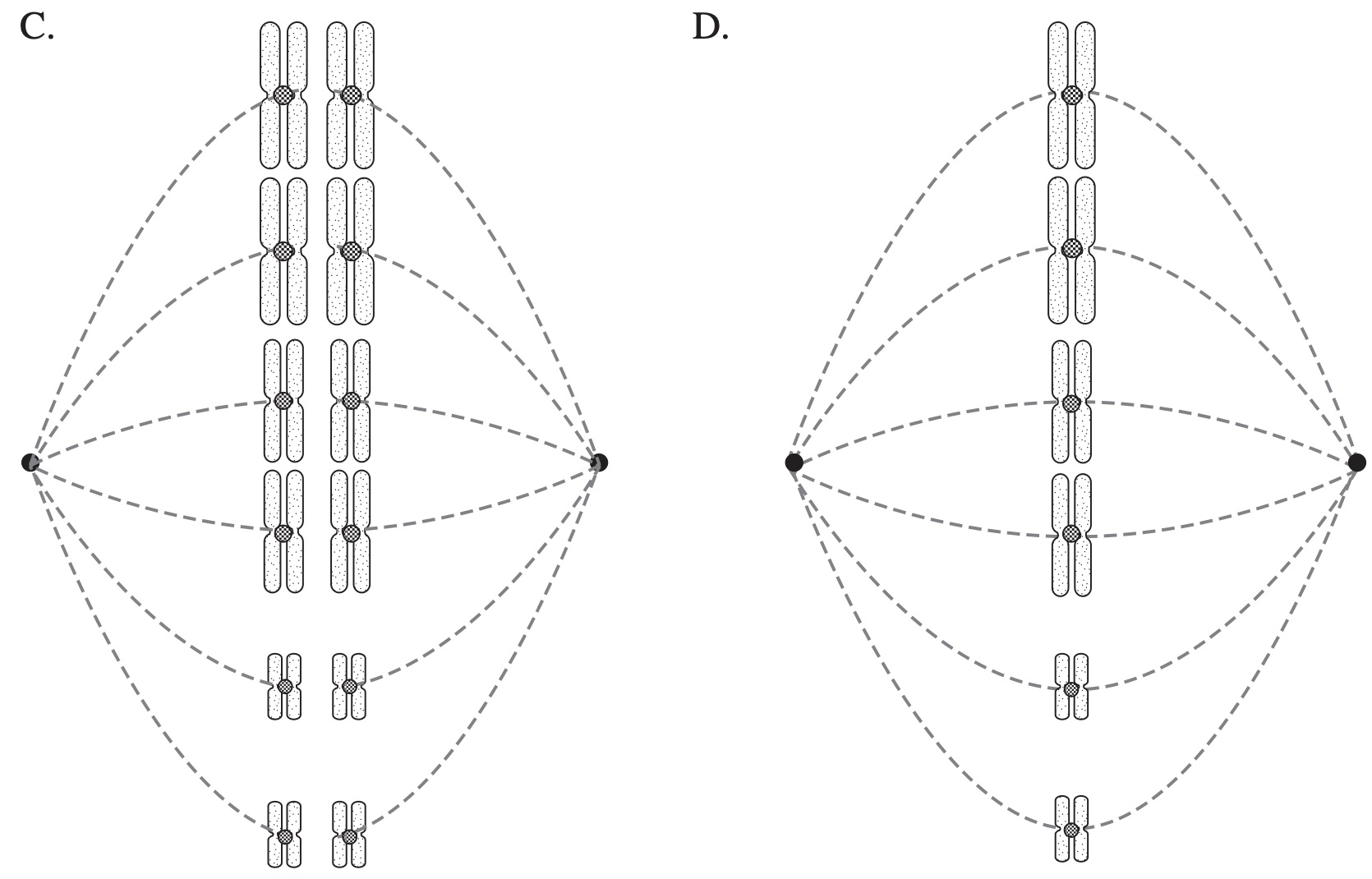
Show Answers Only

`A`

Show Worked Solution

By Elimination:

  • Option D would end up with 12 chromosomes in its somatic cells (Eliminate D).
  • Option B and C show meiosis 1, as they are arranged in tetrads. Option C will end up with 12 chromosomes in its somatic cells, while option B is an incorrect model as it does not correctly display homologous pairs arranging in tetrads. (Eliminate B and C).
  • The diagram in option `A` shows metaphase II of meiosis in a cell with 6 chromosomes.

`=>A`

♦ Mean mark 19%.

BIOLOGY, M6 2020 HSC 18 MC

SNP databases have been used in forensic investigations. One is outlined below.

  1. DNA was collected at a crime scene 30 years ago.
  2. Recently the crime scene DNA was analysed at 700 000 SNP locations.
  3. An SNP profile was created and uploaded to a genealogy database.
  4. The SNP profile from the crime scene indicated some shared SNPs with two individuals (who did not have SNPs in common).
  5. The pedigrees were constructed for the two individuals.
     

Which person is most likely to be the suspect who should be investigated?

  1. `A`
  2. `B`
  3. `C`
  4. `D`
Show Answers Only

`D`

Show Worked Solution
  • Individual `D` is the only individual that shares DNA with both I and II and is the most likely suspect.

`=>D`

♦♦♦ Mean mark 17%.

BIOLOGY, M5 2020 HSC 16 MC

Analysis of DNA shows that adenine and guanine always make up 50% of the total amount of nitrogenous bases in DNA.

Which structural feature of DNA does this provide evidence for?

  1. DNA is helical in structure.
  2. DNA is always a double-stranded molecule.
  3. DNA always has adenine paired with guanine.
  4. DNA is made up of equal amounts of nitrogenous bases.
Show Answers Only

`B`

Show Worked Solution
  • In DNA, adenine always pairs with thymine and guanine always pairs with cytosine.
  • The fact that adenine and guanine make up 50% of the total nitrogenous bases in DNA is therefore evidence that DNA is double stranded (held together by paired bases).

`=>B`

♦ Mean mark 27%.

BIOLOGY, M5 2020 HSC 14 MC

A normal allele results in liver cells with sufficient cholesterol receptors. A different allele results in liver cells without cholesterol receptors. Individuals who are heterozygous have liver cells with insufficient cholesterol receptors.

What type of inheritance is the most likely explanation for this?

  1. Sex-linked
  2. Autosomal dominant
  3. Autosomal recessive
  4. Incomplete dominance
Show Answers Only

`D`

Show Worked Solution
  • A heterozygous individual exhibiting faulty cholesterol receptors suggests that neither allele is completely expressed.
  • There is also no evidence of the condition being sex-linked.

`=>D`

♦♦♦ Mean mark 31%.

BIOLOGY, M6 2021 HSC 33c

Genetically engineered Atlantic salmon have been produced and approved for aquaculture in the US. These salmon have a transgene that includes a protein-coding sequence from a Chinook salmon's growth hormone gene and the promoter region of an Ocean Pout's antifreeze protein gene. The following diagram provides an overview of the production of the transgenic salmon.
 

Transgenic fish can reproduce and pass on the dominant transgene (T).

Reproduction for aquaculture is strictly controlled using a variety of techniques in order to protect and preserve biodiversity.

Some of these techniques are outlined below. 

1. Homozygous (TT) female (XX) breeding stock are kept in quarantine.

2. The female fish undergo hormone treatment that results in sex reversal and the development of male sex organs and sperm.

3. The sperm produced is collected and used to fertilise eggs obtained from wild-type, non-transgenic salmon.

4. The eggs are treated with pressure shock to prevent the completion of meiosis II. As a result, offspring are triploid (three copies of each chromosome).

All offspring are transgenic female fish and have XXX (XXX fish cannot develop sex organs).

5. Offspring are transported to inland aquaculture tanks to be grown to market size.

Analyse how these techniques protect and preserve biodiversity.   (9 marks)

Show Answers Only

Protecting and Preserving Biodiversity:

  • Biodiversity refers to the variety of genes within the gene pool of a species as well as the variety of species within an ecosystem.
  • The nature of the transgenic salmon carries the risk of reducing biodiversity and has the potential to do great harm.
  • If transgenic salmon escape captivity, they may have a survival advantage over natural salmon and other species. In this way, they could outcompete other species and reduce species diversity, as well as outcompete natural salmon.
  • As a result of the transgene being dominant, it will be passed onto offspring, and in time reduce the gene pool.
  • The physical separation techniques 1 and 5 prevent the transgenic salmon from being released into the environment, preserving biodiversity.
  • Reproductive techniques such as the hormone treatment in technique 2 allow sperm to be produced that only carries the X chromosome as the parents are genetically female.
  • This sperm is then used to fertilise from wild-type salmon, and all offspring will be female as sperm does not contain a Y chromosome, and contain the transgene.
  • Technique 4 uses pressure shock to prevent meiosis 2, resulting in infertile, triploid offspring. This produces transgenic salmon incapable of breeding, meaning the transgene cannot be passed on, preserving biodiversity within the gene pool.
  • The use of wild-type salmon eggs to produce transgenic fish is also crucial in preserving biodiversity as it reduces the likelihood of the accumulation of mutations via interbreeding of transgenic salmon.
  • The physical separation techniques of quarantine and inland aquaculture tanks coupled with reproductive techniques are essential biotechnologies to protect and preserve biodiversity from the dangers of transgenic salmon to the ecosystem and gene pool.
Show Worked Solution

Protecting and Preserving Biodiversity:

  • Biodiversity refers to the variety of genes within the gene pool of a species as well as the variety of species within an ecosystem.
  • The nature of the transgenic salmon carries the risk of reducing biodiversity and has the potential to do great harm.
  • If transgenic salmon escape captivity, they may have a survival advantage over natural salmon and other species. In this way, they could outcompete other species and reduce species diversity, as well as outcompete natural salmon.
  • As a result of the transgene being dominant, it will be passed onto offspring, and in time reduce the gene pool.
  • The physical separation techniques 1 and 5 prevent the transgenic salmon from being released into the environment, preserving biodiversity.
  • Reproductive techniques such as the hormone treatment in technique 2 allow sperm to be produced that only carries the X chromosome as the parents are genetically female.
  • This sperm is then used to fertilise from wild-type salmon, and all offspring will be female as sperm does not contain a Y chromosome, and contain the transgene.
  • Technique 4 uses pressure shock to prevent meiosis 2, resulting in infertile, triploid offspring. This produces transgenic salmon incapable of breeding, meaning the transgene cannot be passed on, preserving biodiversity within the gene pool.
  • The use of wild-type salmon eggs to produce transgenic fish is also crucial in preserving biodiversity as it reduces the likelihood of the accumulation of mutations via interbreeding of transgenic salmon.
  • The physical separation techniques of quarantine and inland aquaculture tanks coupled with reproductive techniques are essential biotechnologies to protect and preserve biodiversity from the dangers of transgenic salmon to the ecosystem and gene pool.
♦ Mean mark 44%.

Mechanics, EXT2 M1 2022 HSC 8 MC

As a projectile of mass `m` kilograms travels through air, it experiences a frictional force. The magnitude of this force is proportional to the square of the speed `v` of the projectile. The constant of proportionality is the positive number `k`. The position of the particle at time `t` is denoted by `([x],[y])`. The acceleration due to gravity is `g \ text{m s}^(-2)`.

Based on Newton's laws of motion, which equation models the motion of this projectile?

  1. `([0],[-mg])+kv([overset.x],[overset.y])=m([overset{..}x],[overset{..}y])`
  2. `([0],[-mg])-kv([overset.x],[overset.y])=m([overset{..}x],[overset{..}y])`
  3. `([0],[-mg])+kv^(2)([overset.x],[overset.y])=m([overset{..}x],[overset{..}y])`
  4. `([0],[-mg])-kv^(2)([overset.x],[overset.y])=m([overset{..}x],[overset{..}y])`
Show Answers Only

`B`

Show Worked Solution

`text{Friction}\ (F)\ text{works against velocity}`

`:.\ F prop v^2\ \ =>\ \ F=-kv^2\ \ (k>0)`

`text{→ Eliminate A and C}`
 


♦♦♦ Mean mark 26%.

`text{S}text{ince}\ \ v=abs(((dotx),(doty))):`

`- abs(kv((dotx),(doty))) = -kv abs(((dotx),(doty)))=-kv^2`

`=>B`

BIOLOGY, M8 2021 HSC 31

Millions of people around the world take drugs known as statins, which have been shown to reduce the incidence of heart attacks and strokes in vulnerable patients. However, up to 20% of people stop taking statins due to side-effects such as muscle aches, fatigue, feeling sick and joint pain.

A recent study at a public hospital focused on 60 patients who had all stopped taking statins in the past due to severe side-effects. Patients took statin tablets for four months, placebo tablets for four months and no tablets for four months.

Every day for the year the patients scored, from zero to 100, how bad their symptoms were. The results are shown.
 

Evaluate this study and its results.   (6 marks)

Show Answers Only
  • The data shows that when no tablets were taken, patients still displayed symptoms of the side effects (score 8.0). Taking the statin tablets doubled the severity of the side effects (score 16.3), however, placebo tablets with no active ingredients still produced similar results (score 15.4).
  • This seems to indicate that the side effects may arise as a result of other factors.
  • However, this study cannot be regarded as valid. Only 60 patients were involved in comparison to the millions that take statin tablets.
  • The results were also taken in a qualitative way and cannot be regarded as reliable.
  • The study should also have included a control group of people who have never taken statins to be used for a comparison to improve validity.
  • While the raw data provides data which is valuable and should be followed up with a large, randomised control trial, the study itself cannot be regarded as valid.
Show Worked Solution
  • The data shows that when no tablets were taken, patients still displayed symptoms of the side effects (score 8.0). Taking the statin tablets doubled the severity of the side effects (score 16.3), however, placebo tablets with no active ingredients still produced similar results (score 15.4).
  • This seems to indicate that the side effects may arise as a result of other factors.
  • However, this study cannot be regarded as valid. Only 60 patients were involved in comparison to the millions that take statin tablets.
  • The results were also taken in a qualitative way and cannot be regarded as reliable.
  • The study should also have included a control group of people who have never taken statins to be used for a comparison to improve validity.
  • While the raw data provides data which is valuable and should be followed up with a large, randomised control trial, the study itself cannot be regarded as valid.
♦♦ Mean mark 38%.

PHYSICS, M8 2019 HSC 36

A radon-198 atom, initially at rest, undergoes alpha decay. The masses of the atoms involved are shown in atomic mass units `(u)`. 
 

The kinetic energy of the polonium atom produced is  `2.55 × 10^(-14)` J.

By considering mass defect, calculate the kinetic energy of the alpha particle, and explain why it is significantly greater than that of the polonium atom.   (7 marks)

Show Answers Only
`Delta m` `=197.999-(193.988+4.000260)`  
  `=0.0084\ \text{u}`  
  `=0.0084 xx1.661 xx10^(-27)` (Converting to kg)
  `=1.395 xx10^(-29)\ \text{kg}`  

 

`E` `=mc^2`  
  `=1.395 xx10^(-29)xx(3xx10^(8))^(2)`  
  `=1.256 xx10^(-12)\ \text{J}`  

 
Applying the law of conservation of energy:

   `KE_(text{alpha})` `=E_(text{total})-KE_(polonium)`  
  `=1.256 xx10^(-12)-2.44 xx10^(-14)`  
  `=1.23 xx10^(-12)\ \text{J}`  
     
  •  As the radon atom is initially at rest, the initial momentum of this reaction system is zero. So, by applying the principle of conservation of momentum, the decay products must move away from each other with equal and opposite momenta.
  • The alpha particle has a significantly lower mass compared to the polonium atom and therefore has a significantly higher velocity.
  • `KE=(1)/(2)mv^(2)=(1)/(2)mv xx v`  and the momenta, `mv`  are equal for both the alpha particle and polonium atom. The alpha particle therefore has a significantly greater kinetic energy due to its greater velocity.
Show Worked Solution
`Delta m` `=197.999-(193.988+4.000260)`  
  `=0.0084\ \text{u}`  
  `=0.0084 xx1.661 xx10^(-27)` (Converting to kg)
  `=1.395 xx10^(-29)\ \text{kg}`  

 

`E` `=mc^2`  
  `=1.395 xx10^(-29)xx(3xx10^(8))^(2)`  
  `=1.256 xx10^(-12)\ \text{J}`  

 
Applying the law of conservation of energy:

   `KE_(text{alpha})` `=E_(text{total})-KE_(polonium)`  
  `=1.256 xx10^(-12)-2.44 xx10^(-14)`  
  `=1.23 xx10^(-12)\ \text{J}`  
     
  •  As the radon atom is initially at rest, the initial momentum of this reaction system is zero. So, by applying the principle of conservation of momentum, the decay products must move away from each other with equal and opposite momenta.
  • The alpha particle has a significantly lower mass compared to the polonium atom and therefore has a significantly higher velocity.
  • `KE=(1)/(2)mv^(2)=(1)/(2)mv xx v`  and the momenta, `mv`  are equal for both the alpha particle and polonium atom. The alpha particle therefore has a significantly greater kinetic energy due to its greater velocity.

♦♦♦ Mean mark 30%.

PHYSICS, M8 2019 HSC 34

Use the following information to answer this question.
 

Describe both the production and radiation of energy by the sun. In your answer, include a quantitative analysis of both the power output and the surface temperature of the sun.   (9 marks)

Show Answers Only
  • Production of the sun’s energy is predominantly done through the proton-proton chain.
  • Four protons react in the sun’s core to produce one helium atom. The mass of one helium atom is less than the mass of four protons so mass is converted into energy through Einstein’s mass-energy equivalence, `E=mc^2.`
  • The sun acts as a black body and so radiates its energy in the form of black body radiation.
  • It radiates energy as light with a variety of wavelengths, as shown in the black body curve above. It peaks at a specific wavelength which can be used to calculate its temperature:
  •    `lambda_(max)=5.0xx10^-7` m  (see graph above)
  • Using  `lambda_(max)=(b)/(T)`
  •   `T=(2.898xx10^-3)/(5.0xx10^-7)=5796\ \text{K}`
  • Energy radiated from the sun spreads out over a sphere as it travels away from the sun. The intensity of radiated energy decreases at distances further from the sun, consistent with the inverse square law.
  • Using the intensity of the sun’s radiation at earth, its power output can be calculated using  `P=IA`:
  •    `P=Ixx4pi r^2=1360 xx4xx3.142 xx(1.5 xx10^(11))^(2)=3.85 xx10^(26)\ \text{W}`
Show Worked Solution
  • Production of the sun’s energy is predominantly done through the proton-proton chain.
  • Four protons react in the sun’s core to produce one helium atom. The mass of one helium atom is less than the mass of four protons so mass is converted into energy through Einstein’s mass-energy equivalence, `E=mc^2.`
  • The sun acts as a black body and so radiates its energy in the form of black body radiation.
  • It radiates energy as light with a variety of wavelengths, as shown in the black body curve above. It peaks at a specific wavelength which can be used to calculate its temperature:
  •    `lambda_(max)=5.0xx10^-7` m  (see graph above)
  • Using  `lambda_(max)=(b)/(T)`
  •   `T=(2.898xx10^-3)/(5.0xx10^-7)=5796\ \text{K}`
  • Energy radiated from the sun spreads out over a sphere as it travels away from the sun. The intensity of radiated energy decreases at distances further from the sun, consistent with the inverse square law.
  • Using the intensity of the sun’s radiation at earth, its power output can be calculated using  `P=IA`:
  •    `P=Ixx4pi r^2=1360 xx4xx3.142 xx(1.5 xx10^(11))^(2)=3.85 xx10^(26)\ \text{W}`

♦♦♦ Mean mark 38%.

PHYSICS, M6 2020 HSC 33

A strong magnet of mass 0.04 kg falls 0.78 m under the action of gravity from position `X` above a hollow copper cylinder. It then travels a distance of 0.20 m through the cylinder from `Y` to `Z` before falling freely again.
 

The magnet takes 0.5 seconds to pass through the cylinder. The displacement-time graph of the magnet is shown.
 

Analyse the motion of the magnet by applying the law of conservation of energy.

Your analysis should refer to gravity and the copper cylinder, and include both qualitative and quantitative information.   (9 marks)

Show Answers Only

During the first 0.4 seconds:

  • The magnet is accelerating downwards at 9.8 m s–2 due to gravity.
  • The magnet’s gravitational potential energy is being converted into kinetic energy consistent with the law of conservation of energy.
  • Quantitatively:
  •   `Delta E_(k)= Delta U=mg Delta h=0.04 xx9.8 xx0.78=0.30576\ \text{J}`
  • Hence 0.30576 joules of the magnet’s gravitational potential energy is converted into kinetic energy as it falls under gravity.

As magnet reaches the copper cylinder:

  • Its downwards motion causes the formation of induced currents in the cylinder which produce a magnetic field that opposes the magnet’s motion (Lenz’s law).
  • This causes the magnet to decelerate to 0.4 m s–1 and lose kinetic energy. 
  • Finding the magnets speed before entering the copper cylinder:
`E_(k)` `=(1)/(2)mv^2`  
`0.30576` `=(1)/(2)xx 0.04xx v^2`  
`v` `=3.91\ \text{m s}^{-1}`  

 

  • Quantifying the kinetic energy loss:
`Delta E_(k)` `=(1)/(2)mv^2-(1)/(2)m u^2`  
  `=(1)/(2)xx 0.04xx 3.91^2-(1)/(2)xx 0.04xx 0.4^2`  
  `=0.30256\ \text{J}`  

 

  • Applying the law of conservation of energy shows that 0.30256 J of the magnet’s kinetic energy is being converted to heat energy within the cylinder as the magnet decelerates.
  • Finally, as the magnet passes through the copper cylinder, its gravitational potential energy decreases while its velocity remains constant.
  • Quantifying the decrease in gravitational potential energy:
  •   `Delta U=mg Delta h=0.04xx 9.8xx 0.2=0.0784`
  • Hence, 0.0784 J of the magnet’s gravitational potential energy is converted into heat energy in the cylinder, consistent with the law of conservation of energy.
Show Worked Solution

During the first 0.4 seconds:

  • The magnet is accelerating downwards at 9.8 m s–2 due to gravity.
  • The magnet’s gravitational potential energy is being converted into kinetic energy consistent with the law of conservation of energy.
  • Quantitatively:
  •   `Delta E_(k)= Delta U=mg Delta h=0.04 xx9.8 xx0.78=0.30576\ \text{J}`
  • Hence 0.30576 joules of the magnet’s gravitational potential energy is converted into kinetic energy as it falls under gravity.

As magnet reaches the copper cylinder:

  • Its downwards motion causes the formation of induced currents in the cylinder which produce a magnetic field that opposes the magnet’s motion (Lenz’s law).
  • This causes the magnet to decelerate to 0.4 m s–1 and lose kinetic energy. 
  • Finding the magnets speed before entering the copper cylinder:
`E_(k)` `=(1)/(2)mv^2`  
`0.30576` `=(1)/(2)xx 0.04xx v^2`  
`v` `=3.91\ \text{m s}^{-1}`  

 

  • Quantifying the kinetic energy loss:
`Delta E_(k)` `=(1)/(2)mv^2-(1)/(2)m u^2`  
  `=(1)/(2)xx 0.04xx 3.91^2-(1)/(2)xx 0.04xx 0.4^2`  
  `=0.30256\ \text{J}`  

 

  • Applying the law of conservation of energy shows that 0.30256 J of the magnet’s kinetic energy is being converted to heat energy within the cylinder as the magnet decelerates.
  • Finally, as the magnet passes through the copper cylinder, its gravitational potential energy decreases while its velocity remains constant.
  • Quantifying the decrease in gravitational potential energy:
  •   `Delta U=mg Delta h=0.04xx 9.8xx 0.2=0.0784`
  • Hence, 0.0784 J of the magnet’s gravitational potential energy is converted into heat energy in the cylinder, consistent with the law of conservation of energy.
♦ Mean mark 51%.

PHYSICS M6 2022 HSC 34

Three charged particles, `X, Y` and `Z`, travelling along straight, parallel trajectories at the same speed, enter a region in which there is a uniform magnetic field which causes them to follow the paths shown. Assume that the particles do not exert any significant force on each other.
 


 

Explain the different paths that the particles follow through the magnetic field.   (7 marks)

Show Answers Only
  • The charged particles each experience a force equal to  `F=qvB`  as they travel perpendicular to the magnetic field lines.
  • This force acts perpendicular to the direction of their velocity, so the charged particles undergo uniform circular motion with the force due to the magnetic field acting as a centripetal force.
  • The radii of their paths can be described by the equation:
`F_(c)` `=F_(b)`  
`(mv^2)/(r)` `=qvB`  
`r` `=(mv)/(qB)`  

 

  • As the strength of the magnetic field `(B)` and the speed `(v)` of the particles is the same, their trajectory is only affected by their mass to charge ratio `((m)/(q))`  which affects their radius of motion and their sign, which determines the direction which they deflect.
  • Both `X` and `Y` initially curve upwards, using the right hand palm rule, these must both be positive charges.
  • `Y` has a greater radius than `X`, so `Y`’s charge to mass ratio is greater than `X`’s.
  • `Z` initially curves downwards, using the right hand palm rule, it must have a negative charge.
  • `Z` has the same radius of motion as `X`, so the charge to mass ratios of `Z` and `X` are the same.
  • `Z` has a smaller radius than `Y`, so `Z`’s charge to mass ratio is less than that of `Y`.
Show Worked Solution
  • The charged particles each experience a force equal to  `F=qvB`  as they travel perpendicular to the magnetic field lines.
  • This force acts perpendicular to the direction of their velocity, so the charged particles undergo uniform circular motion with the force due to the magnetic field acting as a centripetal force.
  • The radii of their paths can be described by the equation:
`F_(c)` `=F_(b)`  
`(mv^2)/(r)` `=qvB`  
`r` `=(mv)/(qB)`  

 

  • As the strength of the magnetic field `(B)` and the speed `(v)` of the particles is the same, their trajectory is only affected by their mass to charge ratio `((m)/(q))`  which affects their radius of motion and their sign, which determines the direction which they deflect.
  • Both `X` and `Y` initially curve upwards, using the right hand palm rule, these must both be positive charges.
  • `Y` has a greater radius than `X`, so `Y`’s charge to mass ratio is greater than `X`’s.
  • `Z` initially curves downwards, using the right hand palm rule, it must have a negative charge.
  • `Z` has the same radius of motion as `X`, so the charge to mass ratios of `Z` and `X` are the same.
  • `Z` has a smaller radius than `Y`, so `Z`’s charge to mass ratio is less than that of `Y`.

Mean mark 60%.

PHYSICS M8 2022 HSC 31

Following the Geiger-Marsden experiment, Rutherford proposed a model of the atom.
 


 

Bohr modified this model to explain the spectrum of hydrogen observed in experiments.
 


 

The Bohr-Rutherford model of the atom consists of electrons in energy levels around a positive nucleus.

How do features of this model account for all the experimental evidence above? Support your answer with a sample calculation and a diagram, and refer to energy, forces and photons.   (9 marks)

Show Answers Only

The Geiger-Marsden experiment, which involved firing alpha particles at a thin sheet of gold foil produced results which can be explained by the Bohr-Rutherford model:

  • The majority of fired alpha particles passed through the gold foil undeflected. Rutherford concluded from this that the atom had a small, central nucleus.
  • Some alpha particles were deflected and some of these were deflected at very large angles. Rutherford concluded from this that the nucleus was dense and positively charged exerting a repulsive electromagnetic force on the fired alpha particles.
  • The model accounts for Rutherford’s conclusions, placing electrons in orbits around a small positive nucleus. 

Rutherford’s model alone could not explain the emission spectra of elements such as hydrogen. Bohr’s contribution to the Bohr-Rutherford model amended this:
 

 

  • Bohr proposed that electrons orbited the atomic nucleus in quantised orbits at fixed energies. He proposed that electrons could move from a higher energy orbit (eg. n=1) to a lower energy orbit (n=3) by emitting a photon with energy  `E=hf`  equal to the energy difference between the two orbits.
  • Additionally, he proposed that electrons could move from a lower energy orbit to a higher energy orbit by absorbing a photon with energy  `E=hf`  equal to the energy difference between the two orbits. 
  • This is able to account for the given emission spectra of hydrogen, where emission lines correspond to electron transitions from higher energy orbits to the second energy orbit which produce photons within the spectrum of visible light. 

Using Rydberg’s equation it is possible to predict the emission lines of hydrogen, using an electron moving from the sixth to the second Bohr energy orbit as an example: 

`(1)/(lambda)` `=R((1)/(n_(f)^(2))-(1)/(n_(i)^(2)))`  
  `=(1.097 xx10^7)((1)/(2^(2))-(1)/(6^(2)))`  
  `=(2 xx1.097 xx10^7)/(9)`  
  `=2.438 xx10^6`  
`lambda` `=410  text{nm}`  
     
  •  This value corresponds to the leftmost line on the given spectrum, reflecting how Bohr’s model can account for the emission spectra of hydrogen.
Show Worked Solution

The Geiger-Marsden experiment, which involved firing alpha particles at a thin sheet of gold foil produced results which can be explained by the Bohr-Rutherford model:

  • The majority of fired alpha particles passed through the gold foil undeflected. Rutherford concluded from this that the atom had a small, central nucleus.
  • Some alpha particles were deflected and some of these were deflected at very large angles. Rutherford concluded from this that the nucleus was dense and positively charged exerting a repulsive electromagnetic force on the fired alpha particles.
  • The model accounts for Rutherford’s conclusions, placing electrons in orbits around a small positive nucleus. 

Rutherford’s model alone could not explain the emission spectra of elements such as hydrogen. Bohr’s contribution to the Bohr-Rutherford model amended this:
 

 

  • Bohr proposed that electrons orbited the atomic nucleus in quantised orbits at fixed energies. He proposed that electrons could move from a higher energy orbit (eg. n=1) to a lower energy orbit (n=3) by emitting a photon with energy  `E=hf`  equal to the energy difference between the two orbits.
  • Additionally, he proposed that electrons could move from a lower energy orbit to a higher energy orbit by absorbing a photon with energy  `E=hf`  equal to the energy difference between the two orbits. 
  • This is able to account for the given emission spectra of hydrogen, where emission lines correspond to electron transitions from higher energy orbits to the second energy orbit which produce photons within the spectrum of visible light. 

Using Rydberg’s equation it is possible to predict the emission lines of hydrogen, using an electron moving from the sixth to the second Bohr energy orbit as an example: 

`(1)/(lambda)` `=R((1)/(n_(f)^(2))-(1)/(n_(i)^(2)))`  
  `=(1.097 xx10^7)((1)/(2^(2))-(1)/(6^(2)))`  
  `=(2 xx1.097 xx10^7)/(9)`  
  `=2.438 xx10^6`  
`lambda` `=410  text{nm}`  
     
  •  This value corresponds to the leftmost line on the given spectrum, reflecting how Bohr’s model can account for the emission spectra of hydrogen.

♦ Mean mark 51%.

PHYSICS, M7 2013 HSC 20 MC

The graph shows the maximum kinetic energy `E` with which photoelectrons are emitted as a function of frequency `f` for two different metals `X` and `Y`.
 


 

The metals are illuminated with light of wavelength 450 nm.

What would be the effect of doubling the intensity of this light without changing the wavelength?

  1. For metal `X`, the number of photoelectrons emitted would not change but the maximum kinetic energy would increase.
  2. For metal `X`, the number of photoelectrons emitted would increase but the maximum kinetic energy would remain unchanged.
  3. For both metals `X` and `Y`, the number of photoelectrons emitted would not change but the maximum kinetic energy would increase.
  4. For both metals `X` and `Y`, the number of photoelectrons emitted would increase but the maximum kinetic energy would remain unchanged.
Show Answers Only

 

Show Worked Solution

PHYSICS M6 2022 HSC 19 MC

An AC generator is operated by turning a handle, which rotates a coil in a magnetic field.

The handle is turned at a constant speed and the AC voltage output of the generator causes a light globe connected to it to light up, as shown in Circuit 1.
 


 

A second identical light globe is then connected in series to the generator output, as shown in Circuit 2 . The handle is turned at the same constant speed.
 

Which statement describes and explains the effort required to turn the handle in Circuit 2, compared to Circuit 1 ?

  1. The handle in Circuit 2 is easier to turn because the smaller current in Circuit 2 produces less opposing torque.
  2. The handle in Circuit 2 is easier to turn because the voltage output is shared equally across the two identical light globes.
  3. The handle in Circuit 2 is more difficult to turn because the larger current in Circuit 2 produces more opposing torque.
  4. The handle in Circuit 2 is more difficult to turn because it takes more power to operate the two identical globes than it does to operate the single globe.
Show Answers Only

`A`

Show Worked Solution
  • Circuit 2 has a greater resistance due to the second light globe in series.
  • The current in circuit 2 is smaller.
  • As this current is the induced current which opposes the rotation of the handle, the handle in circuit 2 is easier to turn.

`=>A`


♦♦♦ Mean mark 17%.

PHYSICS M6 2022 HSC 18 MC

A charged oil droplet was observed between metal plates, as shown.
 


 

While the switch was open, the oil droplet moved downwards at a constant speed. After the switch was closed, the oil droplet moved upwards at the same constant speed.

Assume that the only three forces that may act on the oil droplet are the force of gravity, the force due to the electric field and the frictional force between the air and the oil droplet. The magnitudes of these forces are `F_G` (due to gravity), `F_E` (due to the electric field) and `F_F` (due to the frictional force).

Which row of the table shows all the forces affecting the motion of the oil droplet in the direction indicated, and the relationship between these forces?

\begin{align*}
\begin{array}{l}
\rule{0pt}{2.5ex} \ \rule[-1ex]{0pt}{0pt}& \\
\rule{0pt}{2.5ex}\textbf{A.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{B.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{C.}\rule[-1ex]{0pt}{0pt}\\
\rule{0pt}{2.5ex}\textbf{D.}\rule[-1ex]{0pt}{0pt}\\
\end{array}
\begin{array}{|c|c|}
\hline
\rule{0pt}{2.5ex}\text{Downwards motion}\rule[-1ex]{0pt}{0pt}& \text{Upwards motion} \\
\hline
\rule{0pt}{2.5ex}F_{\text{G}}>F_{\text{F}}\rule[-1ex]{0pt}{0pt}&F_{\text{E}}>F_{\text{F}}\\
\hline
\rule{0pt}{2.5ex}F_{\text{G}}>F_{\text{F}}\rule[-1ex]{0pt}{0pt}& F_{\text{E}}>F_{\text{G}}+F_{\text{F}}\\
\hline
\rule{0pt}{2.5ex}F_{\text{G}}=F_{\text{F}}\rule[-1ex]{0pt}{0pt}& F_{\text{G}}=F_{\text{E}} \\
\hline
\rule{0pt}{2.5ex}F_{\text{G}}=F_{\text{F}}\rule[-1ex]{0pt}{0pt}& F_{\text{E}}=F_{\text{G}}+F_{\text{F}} \\
\hline
\end{array}
\end{align*}

Show Answers Only

\(D\)

Show Worked Solution
  • For the droplet to move at a constant speed, the net force acting on it must be zero.
  • For the downwards motion, this means the downwards gravitational force is equal in magnitude to the upwards frictional force (i.e. \(F_{\text{G}}=F_{\text{F}}\)).
  • For the upwards motion, this means the upwards electric force is equal in magnitude to the sum of the downwards frictional and gravitational forces (i.e. \(F_{\text{E}}=F_{\text{G}}+F_{\text{F}}\)).

\(\Rightarrow D\)


♦♦♦ Mean mark 26%.

PHYSICS, M8 2019 HSC 32

Describe how specific experiments have contributed to our understanding of the electron and ONE other fundamental particle.   (5 marks)

Show Answers Only

Millikan’s Oil Drop Experiment:

  • Millikan’s oil drop experiment involved first measuring the terminal velocity of charged oil droplets in a gravitational field and calculating their mass.
  • An electric field was applied to balance the gravitational field, allowing Millikan to find the electric force and hence, charge on an oil droplet.
  • This allowed him to find the charge on an electron as the smallest difference in charges between two oil drops.

Linear accelerator experiment discovering quarks:

  • An experiment involved using a linear accelerator to speed up and fire a beam of electrons at protons. The scattering pattern of the electrons was analysed and was consistent with protons having an internal structure with both positive and negative charges.
  • This contributed to our understanding of the existence of quarks. 

Other possible answers could include:

  • Thomson’s experiment showing the mass to charge ratio of an electron.
  • Experiments involving synchrotrons discovering particles predicted by the standard model of matter, such as the Higgs-Boson.
Show Worked Solution

Millikan’s Oil Drop Experiment:

  • Millikan’s oil drop experiment involved first measuring the terminal velocity of charged oil droplets in a gravitational field and calculating their mass.
  • An electric field was applied to balance the gravitational field, allowing Millikan to find the electric force and hence, charge on an oil droplet.
  • This allowed him to find the charge on an electron as the smallest difference in charges between two oil drops.

Linear accelerator experiment discovering quarks:

  • An experiment involved using a linear accelerator to speed up and fire a beam of electrons at protons. The scattering pattern of the electrons was analysed and was consistent with protons having an internal structure with both positive and negative charges.
  • This contributed to our understanding of the existence of quarks. 

Other possible answers could include:

  • Thomson’s experiment showing the mass to charge ratio of an electron.
  • Experiments involving synchrotrons discovering particles predicted by the standard model of matter, such as the Higgs-Boson.

♦♦ Mean mark 43%.

Statistics, EXT1 S1 2022 HSC 14d

An airline company that has empty seats on a flight is not maximising its profit.

An airline company has found that there is a probability of 5% that a passenger books a flight but misses it. The management of the airline company decides to allow for overbooking, which means selling more tickets than the number of seats available on each flight.

To protect their reputation, management makes the decision that no more than 1% of their flights should have more passengers showing up for the flight than available seats.

Given management's decision and using the attached normal distribution probability table to find a suitable approximation, find the maximum number of tickets that can be sold for a flight which has 350 seats.  (4 marks)

Show Answers Only

`358`

Show Worked Solution

`text{Let}\ \ X=\ text{number of passengers taking a flight}`

`X ~ text{Bin}(n, 0.95)`

`E(X)=0.05,\ \ text{Var}(X)=n(0.95)(1-0.95)=0.0475n`

`X\ text{can be approximated by}\ \ Y ~ N(0.95n, 0.0475n)`
 

`text{Find}\ n\ text{such that}\ \ P(Y>350)=0.01:`

`text{Using the probability table}`

`=> ztext{-score of 2.33 corresponds to (closest) upper tail probability < 0.01}`

`2.33` `=(350-0.95n)/sqrt(0.0475n)`  
`2.33sqrt(0.0475)sqrtn` `=350-0.95n`  

 
`0.95n+2.33sqrt(0.0475)sqrtn-350=0`

`sqrtn` `=(-2.33sqrt(0.0475)+-sqrt((2.33sqrt(0.0475))^2-4(0.95)(-350)))/(2(0.95))`  
  `=18.9288…\ \ (n>0)`  
  `=(18.9288…)^2`  
  `~~358.30`  

  
`:.\ text{Maximum tickets that can be sold = 358}`


♦♦♦ Mean mark 22%.

Vectors, EXT1 V1 2022 HSC 14b

The vectors `\vec{u}` and `\vec{v}` are not parallel. The vector `\vec{p}` is the projection of `\vec{u}` onto the vector `\vec{v}`.

The vector `\vec{p}` is parallel to `\vec{v}` so it can be written `\lambda_0 \vec{v}` for some real number `\lambda_0`. (Do NOT prove this.)

Prove that  `|\vec{u}-\lambda \vec{v}|`  is smallest when `\lambda=\lambda_0` by showing that, for all real numbers `\lambda,\|\vec{u}-\lambda_0 \vec{v}\| \leq|\vec{u}-\lambda \vec{v}|`.  (3 marks)

Show Answers Only

`text{Proof (See Worked Solutions)}`

Show Worked Solution
`overset(->)p` `=text{proj}_(overset(->)v)overset(->)u`  
`lambda_0 overset(->)v` `=(overset(->)u*overset(->)v)/(|overset(->)v|^2) overset(->)v`  
`lambda_0` `=(overset(->)u*overset(->)v)/(|overset(->)v|^2 )\ \ \ …\ (1)`  

 
`text{Show}\ \ |\vec{u}-\lambda_0 \vec{v}\| \leq|\vec{u}-\lambda \vec{v}| :`

`|\vec{u}-\lambda \vec{v}\|^2 -|\vec{u}-\lambda_0 \vec{v}|^2`

`=(vec{u}-\lambda \vec{v})*(vec{u}-\lambda \vec{v})-(vec{u}-\lambda_0 \vec{v})*(vec{u}-\lambda_0 \vec{v})`

`=vec{u}*vec{u}-2lambda vec{u}*vec{v}+lambda^2vec{v}*vec{v}-(vec{u}*vec{u}-2lambda_0vec{u}*vec{v}+lambda_0^2vec{v}*vec{v})`

`=-2lambdavec{u}*vec{v}+lambda^2|vec{v}|^2+2lambda_0vec{u}*vec{v}-lambda_0^2|vec{v}|^2`

`=|vec{v}|^2(lambda^2-lambda_0^2)-2vec{u}*vec{v}(lambda-lambda_0)`

`=|vec{v}|^2(lambda-lambda_0)[lambda+lambda_0-2(vec{u}*vec{v})/|vec{v}|^2]`

`=|vec{v}|^2(lambda-lambda_0)[lambda+lambda_0-2lambda_0]\ \ \ text{(see (1))}`

`=|vec{v}|^2(lambda-lambda_0)^2>=0`
 

`text{S}text{ince}\ \ |\vec{u}-\lambda \vec{v}\|^2 -|\vec{u}-\lambda_0 \vec{v}|^2>=0`

`=>\ |\vec{u}-\lambda_0 \vec{v}|^2<=|\vec{u}-\lambda \vec{v}\|^2 `

`=>\ |\vec{u}-\lambda_0 \vec{v}|<=|\vec{u}-\lambda \vec{v}\| \ \ text{… as required}`

`:. |\vec{u}-\lambda \vec{v}|\ \ text{is smallest when}\ \ lambda=\lambda_0`


♦♦♦ Mean mark 22%.

Calculus, EXT1 C3 2022 HSC 10 MC

Which of the following could be the graph of a solution to the differential equation

`(dy)/(dx)=sin y+1?`
 


 

Show Answers Only

`B`

Show Worked Solution

`text{One Strategy}`

`text{When}\ \ (dy)/(dx)=0:`

`siny=-1\ \ =>\ \ y=(3pi)/2 + 2kpi\ \ (kinZZ)`

`text{Graphically,}\ \ y=(3pi)/2 + 2kpi\ \ text{are horizontal asymptotes.}`

`=>B`


♦♦♦ Mean mark 27%.

Calculus, EXT1 C2 2022 HSC 9 MC

A given function  `f(x)`  has an inverse  `f^{-1}(x)`.

The derivatives of  `f(x)`  and  `f^{-1}(x)`  exist for all real numbers `x`.

The graphs  `y=f(x)`  and  `y=f^{-1}(x)`  have at least one point of intersection.

Which statement is true for all points of intersection of these graphs?

  1. All points of intersection lie on the line  `y=x`.
  2. None of the points of intersection lie on the line  `y=x`.
  3. At no point of intersection are the tangents to the graphs parallel.
  4. At no point of intersection are the tangents to the graphs perpendicular.
Show Answers Only

`D`

Show Worked Solution

`text{By Elimination:}`

`text{Consider}\ \ f(x)=x\ \ =>\ \ f^(-1)(x)=x:`

`text{All POI lie on}\ \ y=x\ \ text{and all tangents are parallel}`

`text{→ Eliminate B and C}`
 

`text{Consider}\ \ f(x)=-x\ \ =>\ \ f^(-1)(x)=-x:`

`text{All POI lie on}\ \ y=-x`

`text{→ Eliminate A}`

`=>D`


♦♦♦ Mean mark 13%.

Financial Maths, 2ADV M1 2022 HSC 32

In a reducing-balance loan, an amount `$P` is borrowed for a period of `n` months at an interest rate of 0.25% per month, compounded monthly. At the end of each month, a repayment of `$M` is made. After the `n`th repayment has been made, the amount owing, `$A_n`, is given by

`A_(n)=P(1.0025)^(n)-M(1+(1.0025)^(1)+(1.0025)^(2)+cdots+(1.0025)^(n-1))`

(Do NOT prove this.)

  1. Jane borrows $200 000 in a reducing-balance loan as described.

  2. The loan is to be repaid in 180 monthly repayments.

  3. Show that  `M` = 1381.16, when rounded to the nearest cent.  (2 marks)

  4. After 100 repayments of $1381.16 have been made, the interest rate changes to 0.35% per month.

  5. At this stage, the amount owing to the nearest dollar is $100 032. (Do NOT prove this.)

  6. Jane continues to make the same monthly repayments.

  7. For how many more months will Jane need to make full monthly payments of $1381.16?  (3 marks)

  8. The final payment will be less than $1381.16.
  9. How much will Jane need to pay in the final payment in order to pay off the loan?   (2 marks)

Show Answers Only
  1. `text{Proof (See Worked Solutions)}`
  2. `83`
  3. `$931.54`
Show Worked Solution

a.   `text{Show}\ \ M=$1381.16`

`A_(n)` `=P(1.0025)^(n)-M(1+(1.0025)^(1)+(1.0025)^(2)+cdots+(1.0025)^(n-1))`  
`0` `=200\ 000(1.0025)^180-M underbrace((1+(1.0025)^(1)+(1.0025)^(2)+cdots+(1.0025)^179))_(text(GP where)\ a = 1,\ r = 1.0025,\ n = 180)`  
`0` `=200\ 000(1.0025)^180-M((1(1.0025^180- 1))/(1.0025-1))`  

`M((1.0025^180-1)/(1.0025-1))=200\ 000(1.0025)^180`

`:.M` `=200\ 000(1.0025)^180 -: (1.0025^180-1 )/(1.0025-1)`   
  `=1381.163…`  
  `=$1381.16\ \ text{… as required}`  

 

b.   `P=$100\ 032,\ \ r=1.0035  and M=$1381.16`

`text{Find}\ \ n\ \ text{when}\ \ A_n=0:`

`A_(n)` `=P(1.0035)^(n)-1381.16(1+(1.0035)^(1)+(1.0035)^(2)+cdots+(1.0035)^(n-1))`  
`0` `=100\ 032(1.0035)^n-1381.16 ((1.0035^n- 1)/(1.0035-1))`  
`0` `=100\ 032(1.0035)^n-1381.16/0.0035 (1.0035^n- 1)`  
  `=100\ 032(1.0035)^n-394\ 617(1.0035)^n- 394\ 617`  
`294\ 585(1.0035)^n` `=394\ 617`  
`1.0035^n` `=(394\ 617)/(294\ 585)`  
`n` `=ln((394\ 617)/(294\ 585))/ln1.0035`  
  `=83.674…`  
  `=83\ text{more months with full payment}`  

 


♦♦ Mean mark part (b) 38%.

c.   `text{Find}\ \ A_83:`

`A_83` `=100\ 032(1.0035)^83-1381.16 ((1.0035^83- 1)/(1.0035-1))`  
  `=928.291…`  

 
`text{Interest will be added for the last month:}`

`:.\ text{Final payment}` `=928.291… xx 1.0035`  
  `=$931.54`  

♦♦♦ Mean mark part (c) 14%.

Calculus, 2ADV C3 2022 HSC 31

A line passes through the point  `P(1,2)`  and meets the axes at  `X(x, 0)`  and  `Y(0, y)`, where `x>1`.
 

  1. Show that  `y=(2x)/(x-1)`.  (2 marks)

  2. Find the minimum value of the area of triangle `XOY`.  (4 marks)

Show Answers Only
  1. `text{Proof (See Worked Solutions)}`
  2. `4\ text{u}^2`
Show Worked Solution

a.   `text{Show}\ \ y=(2x)/(x-1)`

`text{S}text{ince}\ \ m_(YP)=m_(PX):`

`(y-2)/(0-1)` `=(2-0)/(1-x)`  
`y-2` `=(-2)/(1-x)`  
`y` `=2-2/(1-x)`  
  `=(2(1-x)-2)/(1-x)`  
  `=(-2x)/(1-x)`  
  `=(2x)/(x-1)\ \ text{… as required}`  

 


♦♦♦ Mean mark part (a) 17%.
COMMENT: `y=(2x)/(x-1)` is the expression of a relationship between the intercepts and not the equation of the line.
b.    `A` `=1/2 xx b xxh`
    `=1/2x((2x)/(x-1))`
    `=(x^2)/(x-1)`

 

`(dA)/dx` `=((x-1)*2x-x^2(1))/((x-1)^2)`  
  `=(2x^2-2x-x^2)/((x-1)^2)`  
  `=(x(x-2))/((x-1)^2)`  

 
`text{SP’s occur when}\ \ (dA)/dx=0:`

`x=0\ \ text{or}\ \ 2`
 

`text{Use 1st derivative test to find max/min:}`

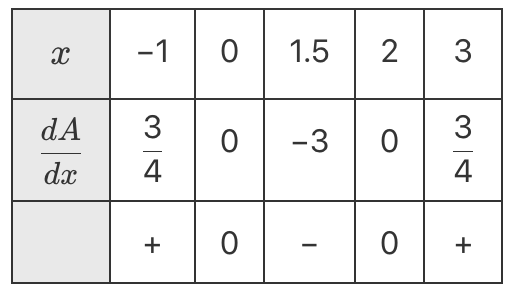
`=>\ text{MIN at}\ \ x=2`

`:.A_min` `=1/2 xx 2 xx (2xx2)/(2-1)`  
  `=4\ text{u}^2`  

♦♦ Mean mark part (b) 29%.

Statistics, 2ADV S3 2022 HSC 30

A continuous random variable \(X\) has cumulative distribution function given by

\(F(x)= \begin{cases}
1 & x>e^3 \\
\ \\
\dfrac{1}{k}\, \ln x & 1 \leq x \leq e^3 . \\
\ \\
0 & x<1\end{cases}\)

  1. Show that  \(k = 3\).  (1 mark)

  2. Given that  \(P(X < c)=2P(X > c)\), find the exact value of \(c\).  (2 marks)

Show Answers Only
  1. \(\text{Proof (See Worked Solutions)}\)
  2. \(e^2\)
Show Worked Solution

a.  \(\text{Show} \ \ k=3\)

\begin{aligned}
{\left[\dfrac{1}{k} \, \ln x\right]_1^{e^3} } & =1 \\
\dfrac{1}{k}\, \ln \left(e^3\right)-\dfrac{1}{k}\, \ln 1 & =1 \\
\dfrac{1}{k}(3)-\frac{1}{k}(0) & =1 \\
k & =3 \ldots \text{as required}
\end{aligned}


♦♦ Mean mark (a) 38%.
b.    \(P(X<c)\) \(=\left[\dfrac{1}{3}\, \ln x\right]_0^c\)
    \(=\dfrac{1}{3}\, \ln c\)

\begin{aligned}
2 P(X>c) & =2 P(1-P(X<c)) \\
& =2\left(1-\frac{1}{3} \ln c\right)
\end{aligned}

\(\text { Given } P(X<c)=2 P(X>c)\)

\begin{aligned}
\dfrac{1}{3}\, \ln c & =2-\dfrac{2}{3}\, \ln c \\
\ln c & =2 \\
\therefore c & =e^2
\end{aligned}


♦♦♦ Mean mark (b) 19%.

Calculus, 2ADV C4 2022 HSC 29

  1. The diagram shows the graph of  `y=2^{-x}`. Also shown on the diagram are the first 5 of an infinite number of rectangular strips of width 1 unit and height  `y=2^{-x}`  for non-negative integer values of `x`. For example, the second rectangle shown has width 1 and height `(1)/(2)`. 
     


 

  1. The sum of the areas of the rectangles forms a geometric series.
  2. Show that the limiting sum of this series is 2. (1 mark)

  3. Show that `int_(0)^(4)2^(-x)\ dx=(15)/(16 ln 2)`.  (2 marks)

  4. Use parts (a) and (b) to show that  `e^(15) < 2^(32)`.  (2 marks)

Show Answers Only
  1. `text{Proof (See Worked Solutions)}`
  2. `text{Proof (See Worked Solutions)}`
  3. `text{Proof (See Worked Solutions)}`
Show Worked Solution

a.   `text{Consider the rectangle heights:}`

`2^0=1, \ 2^(-1)=1/2, \ 2^(-2)= 1/4, \ 2^(-3)= 1/8, …`

`=>\ text{Rectangle Areas}\ = 1, \ 1/2, \  1/4, \ 1/8, …`

`a=1,\ \ r=1/2`

`S_oo=a/(1-r)=1/(1-1/2)=2\ \ text{… as required}`
 

b.   `text{Show}\ \ int_0^4 2^(-x)\ dx = 15/(16ln2)`

`int_0^4 2^(-x)\ dx ` `=(-1)/ln2[2^(-x)]_0^4`  
  `=(-1)/ln2(1/16-1)`  
  `=1/ln2-1/(16ln2)`  
  `=(16-1)/(16ln2)`  
  `=15/(16ln2)\ \ text{… as required}`  

 


Mean mark (b) 56%.

c.   `text{Show}\ \ e^15<2^32`

`text{Area under curve < Sum of rectangle areas}`

`15/(16ln2)` `<2`  
`15` `<32ln2`  
`15/32` `<ln2`  
`e^(15/32)` `<e^(ln2)`  
`root(32)(e^15)` `<2`  
`e^15` `<2^32\ \ text{… as required}`  

♦♦♦ Mean mark (c) 9%.

Probability, 2ADV S1 2022 HSC 9 MC

Liam is playing two games. He is equally likely to win each game. The probability that Liam will win at least one of the games is 80%.

Which of the following is closest to the probability that Liam will win both games?

  1.  31%
  2.  40%
  3.  55%
  4.  64%
Show Answers Only

`A`

Show Worked Solution

`Ptext{(at least 1 W)}\ = 1-Ptext{(LL)}\ =0.8`

`Ptext{(LL)}` `=0.2`  
`Ptext{(L)}` `=sqrt0.2`  
  `=0.447`  

 

`Ptext{(W)}` `=1-0.447=0.553`  
`Ptext{(WW)}` `=(0.553)^2`  
  `=0.31`  

`=>A`


… Mean marks/comments here
♦♦♦ Mean mark 27%.

Financial Maths, STD2 F4 2022 HSC 36

Frankie borrows $200 000 from a bank. The loan is to be repaid over 23 years at a rate of 7.2% per annum, compounded monthly. The repayments have been set at $1485 per month.

The interest charged and the balance owing for the first three months of the loan are shown in the spreadsheet below.
 

  1. What are the values of `A` and `B`?  (2 marks)
  2. After 50 months of repaying the loan, Frankie decides to make a lump sum payment of $ 40 000 and to continue making the monthly repayments of $1485. The loan will then be fully repaid after a further 146 monthly repayments.
  3. How much less will Frankie pay overall by making the lump sum payment?  (3 marks)
Show Answers Only
  1. `A=$1198.29,\ \ B=$199\ 139.86`
  2. `$78\ 800`
Show Worked Solution

a.   `text{Monthly interest rate}\ =7.2/12=0.6text{%}`

`A` `=199\ 715 xx 0.6/100`  
  `=$1198.29`  

 

`B` `=P+I-R`  
  `=199\ 428.29 + 1196.57-1485`  
  `=$199\ 139.86`  

 

b.   `text{Total payments if lump sum not paid}`

`= (23xx12) xx 1485`

`=$409\ 860`
 

`text{Total payments if lump sum paid}`

`=40\ 000 + (50 + 146) xx 1485`

`=$331\ 060`
 

`text{Savings by paying the lump sum}`

`=409\ 860-331\ 060`

`=$78\ 800`


♦♦♦ Mean mark (b) 17%.
 

Statistics, STD2 S1 2022 HSC 15 MC

The cumulative frequency graph shows the distribution of the number of movie downloads made by 100 people in one month.
 

Which box-plot best represents the same data as displayed in the cumulative frequency graph?
 

Show Answers Only

`C`

Show Worked Solution

`text{1st quartile}\ ~~ 3`

`text{Median}\ ~~ 6`

`text{3rd quartile}\ ~~ 7`

`=>C`


♦♦♦ Mean mark 30%.

Statistics, STD2 S5 2022 HSC 13 MC

A random variable is normally distributed with mean 0 and standard deviation 1 . The table gives the probability that this random variable lies below `z` for some positive values of `z`.
 

The probability values given in the table are represented by the shaded area in the following diagram.

What is the probability that a normally distributed random variable with mean 0 and standard deviation 1 lies between 0 and 1.94 ?

  1. 0.0262
  2. 0.4738
  3. 0.5262
  4. 0.9738
Show Answers Only

`B`

Show Worked Solution

`P(z<1.94) = 0.9738`

`P(z<0) = 0.5`

`:. P(0.5<z<1.94) = 0.9738-0.5 = 0.4738`

`=> B`


♦♦♦ Mean mark 22%.

PHYSICS, M6 2019 HSC 18 MC

A circular loop of wire is connected to a battery and a lamp. The apparatus is moved from `P` to `Q` along the path shown at a constant velocity through a region containing a uniform magnetic field.
 

Which graph shows the brightness of the lamp as the apparatus moves between `P` and `Q` ?
 

Show Answers Only

`B`

Show Worked Solution
  • Initially, the current travels clockwise through the loop of wire. As it enters the magnetic field, an anticlockwise current is induced in the loop in order to induce a magnetic field out of page, opposing the external magnetic field (Lenz’s Law).
  • This decreases the net current through the loop, causing a decrease in brightness.
  • As the loop exits the magnetic field, a clockwise current is induced to create a magnetic field into the page, opposing the decrease in magnetic flux passing through it (Lenz’s Law).
  •  This increases the net current in the loop, causing an increase in brightness.

`=>B`


♦♦♦ Mean mark 25%.

PHYSICS, M8 2019 HSC 8 MC

A typical galaxy has a diameter of 100 000 light years (∼30 000 pc).

Which graph is consistent with Hubble's measurements of the recessional velocity of galaxies?
 

 

Show Answers Only

`A`

Show Worked Solution

By elimination:

  • Hubble found that the recessional velocity of a galaxy was directly proportional to its distance (linear graph) → Eliminate C and D
  • Hubble measured distance using parsecs → Eliminate B

`=>A`


♦ Mean mark 25%.

CHEMISTRY, M6 2021 HSC 20 MC

The trimethylammonium ion, \(\ce{[({CH_3)_3NH}]^+}\), is a weak acid. The acid dissociation equation is shown.

\(\ce{[(CH3)3NH]+($aq$)+H2O($l$)\rightleftharpoons  H3O+($aq$)+(CH3)3N($aq$)} \quad K_a = 1.55 \times 10^{-10}\)

At 20°C, a saturated solution of trimethylammonium chloride, \(\ce{[(CH_3)_3NH]Cl}\), has a pH of 4.46.

What is the \(K_{sp}\) of trimethylammonium chloride?

  1. \(1.26 \times 10^{-9}\)
  2. \(7.76\)
  3. \(60.2\)
  4. \(5.01 \times 10^{10}\)
Show Answers Only

\(C\)

Show Worked Solution

\(\ce{\left[\left(CH3\right)_3 NH \right]^{+}(aq)+ H2O(l) \leftrightharpoons H3O ^{+}(aq)+\left(CH3\right)_3 N(aq)}\)

   \(K_a=\dfrac{\left[\left(\text{CH}_3\right)_3 \text{N}\right]\left[ \text{H}_3 \text{O} ^{+}\right]}{\left[\left( \text{CH} _3\right)_3 \text{NH} \right]^{+}}\)
 

\(\text{Calculate}\ K_{sp}:\)

\(\ce{\left[\left(CH _3\right)_3 NH \right] Cl (s) \leftrightharpoons\left[\left( CH _3\right)_3 NH \right]^{+}(aq)+ Cl ^{-}(aq)}\)

   \(K_{sp}=\ce{[(CH3)_3NH)^+] [Cl^-]}\)

\(\text{pH} = \ce{4.46 \rightarrow \left[H3O^+\right] = 10^{-4.46}}\)
  

\(\text{Using stoichiometry;}\)

\(\ce{[(CH3)_3N)^+]=[H3O^+] = 10^{-4.46}}\)

 
\(\text{Using}\ K_{a}:\)

\(1.55 \times 10^{-10}=\dfrac{\left(10^{-4.46} \times 10^{-4.46}\right)}{\ce{\left(CH3\right)3NH^{+}}}\)

\(\ce{\left[\left(\left(CH3\right)_3NH \right)^{+}\right]}=\dfrac{\left(10^{-4.46} \times 10^{-4.46}\right)}{1.55 \times 10^{-10}}=7.7565 \ldots  \text{mol L}^{-1}\)
 

\(\ce{\left[Cl^{-}\right]=\left[\left(\left( CH3\right)_3NH\right)^{+}\right]}=7.7565 \ldots \text{mol L}^{-1}\)

\(\therefore K_{sp}=\ce{\left[\left(\left(CH3\right)_3NH\right)^{+}\right]\times\left[Cl^{-}\right]=7.7565 \ldots \times 7.7565 \ldots=60.2}\)

\(\Rightarrow C\)


♦♦♦ Mean mark 19%.

CHEMISTRY, M8 2021 HSC 9 MC

The amount of paracetamol in a sample needs to be determined.

The UV absorption spectrum of paracetamol is shown.
 

Based on the absorption spectra provided, which solvent should be used to determine the amount of paracetamol?
 

 

Show Answers Only

`D`

Show Worked Solution
  • The solvent used shouldn’t have an absorption spectrum with a maximum that corresponds to that of the paracetamol.
  • This is to ensure that the absorption of solvent will have little to no impact on the measured absorption of the paracetamol sample.

`=> D`


♦♦♦ Mean mark 24%.

PHYSICS, M6 2020 HSC 19 MC

A conductor `P Q` is in a uniform magnetic field. The conductor rotates around the end `P` at a constant angular velocity.
 

Which graph shows the induced emf between `P` and `Q` as the conductor completes one revolution from the position shown?
 

 

Show Answers Only

`C`

Show Worked Solution
  • At the starting position shown, electrons in the rod are moving to the right, parallel to the magnetic field lines. So, there is no force acting on the conductor (EMF of zero).
  • After a quarter of a rotation, electrons in the rod are moving up the page. Using the right hand palm rule, they experience a force out of the page. This will not induce an EMF between `P` and `Q.`
  • The correct graph will show an EMF of zero at both `t=0` and after a quarter of a rotation.

`=>C`


♦♦ Mean mark 10%.

PHYSICS, M7 2020 HSC 18 MC

An observer sees Io complete one orbit of Jupiter as Earth moves from `P_1` to `P_2`, and records the observed orbital period as `t_p`. Similarly, the time for one orbit of Io around Jupiter was measured as Earth moved between the pairs of points at `Q`, `R` and `S`, with the corresponding measured periods of Io being `t_Q`, `t_R` and `t_S`.
 

Which measurement of the orbital period would be the longest?

  1. `t_P`
  2. `t_Q`
  3. `t_R`
  4. `t_S`
Show Answers Only

`B`

Show Worked Solution

When the Earth is travelling between the pairs of points at `Q `, it is moving away from Jupiter:

  • light must travel further to signal the end of an orbit than it does to signal the start of an orbit.
  • `t_(Q)`  would be the longest measured orbital period.

`=>B`


♦ Mean mark 21%.

PHYSICS, M8 2020 HSC 16 MC

A model of the core of a nuclear fission reactor is shown.
 

When the reactor is operating normally, the moderator, control rods and coolant work in combination to maintain a controlled nuclear reaction in the fuel rods.

The moderator is a liquid which slows down neutrons to increase the rate of fission. The control rods absorb free neutrons. The coolant reduces the core temperature.

A fault causes some of the moderator to leak out of the core.

Which action would compensate for the effect of the loss of moderator?

  1. Withdraw the control rods from the core.
  2. Lower the control rods further into the core.
  3. Pump the coolant through the core at a faster rate.
  4. Reduce the temperature of the coolant before pumping it into the core.
Show Answers Only

`A`

Show Worked Solution
  • Loss of moderator leads to a reduction in the rate of fission.
  • Withdrawing the control rods decreases the amount of neutrons absorbed, increasing the rate of fission.

`=>A`

♦ Mean mark 25%.

PHYSICS, M7 2021 HSC 33

Two experiments are performed with identical light sources having a wavelength of 400 nm.

In experiment \(A\), the light is incident on a pair of narrow slits  5.0 × 10\(^{-5}\) m  apart, producing a pattern on a screen located 3.0 m behind the slits.
 

In experiment \(B\), the light is incident on different metal samples inside an evacuated tube as shown. The kinetic energy of any emitted photoelectrons can be measured.
 

Some results from experiment \(B\) are shown.
 

\begin{array}{|l|l|c|}
\hline
\rule{0pt}{1.5ex}\textit{Metal sample}\rule[-0.5ex]{0pt}{0pt}& \textit{Work function} \ \text{(J)} & \textit{Photoelectrons observed?} \\
\hline
\rule{0pt}{2.5ex}\text{Nickel}\rule[-1ex]{0pt}{0pt}&8.25 \times 10^{-19}&\text{No}\\
\hline
\rule{0pt}{2.5ex}\text{Calcium}\rule[-1ex]{0pt}{0pt}& 4.60 \times 10^{-19}&\text{Yes}\\
\hline
\end{array}

How do the results from Experiment \(A\) and Experiment \(B\) support TWO different models of light? In your answer, include a quantitative analysis of each experiment.   (9 marks)

Show Answers Only
  • Experiment A supports the wave model of light as it demonstrates light undergoing diffraction as well as constructive and destructive interference, which are wave properties.
  • When light is incident upon the slits, it diffracts and causes the slit to act as a source of wavefronts. When light from the slits arrives at the screen, bright bands are produced when light waves arrive in phase and undergo constructive interference.
  • Dark bands are produced when light waves arrive at the screen out of phase and undergo destructive interference.
  • The spacing between adjacent bright bands can be calculated using  \(d \sin \theta=m \lambda\):
  •    \(5 \times 10^{-5} \sin \theta=1 \times 400 \times 10^{-9}\ \ \Rightarrow\ \ \theta=0.46^{\circ}\)
  •    \(s=3 \times \tan (0.46^{\circ})=0.024 \ \text{m}\)
  •  Experiment B supports Einstein’s particle, or photon model of light. This model can calculate the photon energy of incident light and explain why photons are emitted from calcium but not nickel:
  •    \(f=\dfrac{c}{\lambda}=\dfrac{3.00 \times 10^8}{400 \times 10^{-9}}=7.50 \times 10^{14} Hz\)
  •    \(E=h f=6.626 \times 10^{-34} \times 7.50 \times 10^{14}=4.97 \times 10^{-19} J\)
  • This energy is greater than the work function of calcium, explaining why one photon has enough energy to liberate a photoelectron from the calcium sample. However, this energy is less than the work function of nickel, explaining why no photoelectrons were observed from the nickel sample.
  • These observations support the particle model of light. Applying the particle model, the kinetic energy of photoelectrons emitted from calcium can be calculated:
  •    \(K_{\max }=h f-\phi=4.97 \times 10^{-19}-4.60 \times 10^{-19}=3.70 \times 10^{-20} \ \text{J}\)
Show Worked Solution
  • Experiment A supports the wave model of light as it demonstrates light undergoing diffraction as well as constructive and destructive interference, which are wave properties.
  • When light is incident upon the slits, it diffracts and causes the slit to act as a source of wavefronts. When light from the slits arrives at the screen, bright bands are produced when light waves arrive in phase and undergo constructive interference.
  • Dark bands are produced when light waves arrive at the screen out of phase and undergo destructive interference.
  • The spacing between adjacent bright bands can be calculated using  \(d \sin \theta=m \lambda\):
  •    \(5 \times 10^{-5} \sin \theta=1 \times 400 \times 10^{-9}\ \ \Rightarrow\ \ \theta=0.46^{\circ}\)
  •    \(s=3 \times \tan (0.46^{\circ})=0.024 \ \text{m}\)
  •  Experiment B supports Einstein’s particle, or photon model of light. This model can calculate the photon energy of incident light and explain why photons are emitted from calcium but not nickel:
  •    \(f=\dfrac{c}{\lambda}=\dfrac{3.00 \times 10^8}{400 \times 10^{-9}}=7.50 \times 10^{14} Hz\)
  •    \(E=h f=6.626 \times 10^{-34} \times 7.50 \times 10^{14}=4.97 \times 10^{-19} J\)
  • This energy is greater than the work function of calcium, explaining why one photon has enough energy to liberate a photoelectron from the calcium sample. However, this energy is less than the work function of nickel, explaining why no photoelectrons were observed from the nickel sample.
  • These observations support the particle model of light. Applying the particle model, the kinetic energy of photoelectrons emitted from calcium can be calculated:
  •    \(K_{\max }=h f-\phi=4.97 \times 10^{-19}-4.60 \times 10^{-19}=3.70 \times 10^{-20} \ \text{J}\)

♦ Mean mark 52%.

PHYSICS, M7 2021 HSC 20 MC

A metal cylinder is located in a uniform magnetic field. The work function of the metal is `phi`.

Photons having an energy of 2`phi` strike the side of the cylinder, liberating photoelectrons which travel perpendicular to the magnetic field in a circular path. The maximum radius of the path is `r`.
 

If the photon energy is doubled, what will the maximum radius of the path become?

  1. `2r`
  2. `3r`
  3. `sqrt2r`
  4. `sqrt3r`
Show Answers Only

`D`

Show Worked Solution
`K_max` `=(1)/(2)mv_(max)^2`  
`v_(max)` `=sqrt((2K_(max))/(m))\ \ `… (1)  

  
Substitute (1) into  `r=(mv)/(qB)`:

    `r=(m)/(qB)sqrt((2K_(max))/(m))`

    `r prop sqrt(K_(max))`
 

  • When the photon energy is `2phi, K_max=phi.`
  • When the photon energy is doubled to `4phi, K_max=3phi.`
  • ∴ Since  `r prop sqrt(K_(max)) ` the radius increases by a factor of `sqrt(3).`

`=>D`


♦ Mean mark 24%.

PHYSICS, M5 2021 HSC 14 MC

Which of the following statements correctly describes the gravitational interaction between the Earth and the Moon?

  1. The Earth accelerates towards the Moon.
  2. The net force acting on the Earth is zero.
  3. The Moon and Earth experience equal and opposite accelerations.
  4. The force acting on the Moon is smaller than the force acting on the Earth.
Show Answers Only

`A`

Show Worked Solution
  • According to Newton’s Third Law, the earth and moon experience equal forces in opposite directions. This causes them to accelerate towards each other.

`=>A`


♦ Mean mark 19%.

PHYSICS, M6 2021 HSC 10 MC

A strong magnet is moved past a copper block at a constant speed as shown.
 

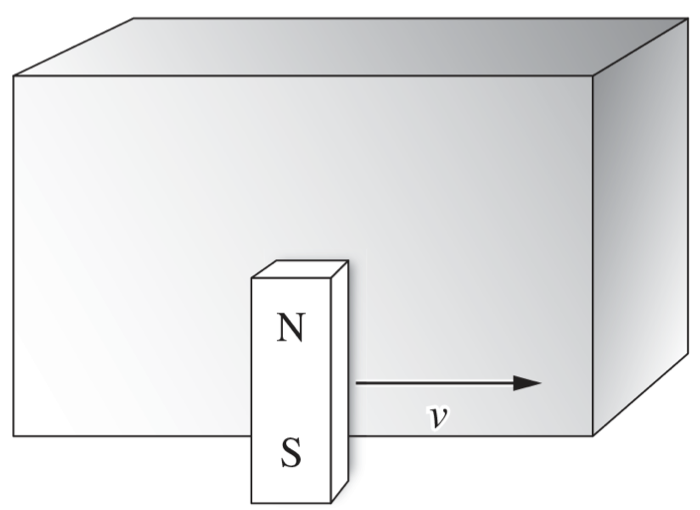
What is the direction of the force acting on the copper block?

  1. To the left
  2. To the right
  3. Into the page
  4. Out of the page
Show Answers Only

`B`

Show Worked Solution
  • Eddy currents will be induced in the copper block. According to Lenz’s Law, this will produce a force that opposes the motion of the magnet.
  • This is done by minimising the relative motion between the block and the magnet, producing a force on the copper block to the right.

`=>B`


♦♦♦ Mean mark 18%.

CHEMISTRY, M5 2021 HSC 11 MC

Consider this system in a fixed volume at constant temperature.

\(\ce{PCl5}(s)\rightleftharpoons \ce{PCl3}(l) + \ce{Cl2}(g)\) 

This system is initially at equilibrium. A small amount of solid \(\ce{PCl5}\) is added.

Which statement is correct?

  1. The amount of \(\ce{Cl2}\) will increase.
  2. The amount of \(\ce{PCl3}\) will decrease.
  3. The amount of \(\ce{Cl2}\) will not change.
  4. The amount of \(\ce{PCl5}\) will increase then decrease.
Show Answers Only

`C`

Show Worked Solution

The equilibrium constant expression is:  `text{K}_(eq) = [text{Cl}_(2)(g)]`

  • As we can see from the equilibrium constant expression, the value of `text{K}_(eq)` is only dependent on the concentration of `text{Cl}_(2)`.
  • As a result, the addition of solid `text{PCl}_5\` will have no affect on the value of `text{K}_(eq)` and thus has no impact on the equilibrium position.
  • Thus, the amount of `text{Cl}_(2)` will not change.

`=> C`


♦♦♦ Mean mark 19%.

CHEMISTRY, M6 2021 HSC 6 MC

Which row of the table describes what happens when a solution of a weak acid is diluted? (Assume constant temperature.)
 

Show Answers Only

`C`

Show Worked Solution

A weak acid has the following equilibrium:

   `text{HA} (aq) + text{H}_2 text{O} (l) ⇋ text{A}^(-) (aq) + text{H}_3 text{O}^(+) (aq)`

   `text{K}_a =  [[text{A}^(-)][text{H}_3text{O}^(+)] ]/[[text{HA}]]`

  • The value of  `text{K}_a` is only affected by temperature, and thus the value of `text{K}_a` will remain the same.
  • When the solution is diluted, water is added. According to Le Chatelier’s Principle, the equilibrium will shift to the right to counteract the change.
  • Thus, the equilibrium will shift to the right and increase the extent of ionisation.

`=>C`


♦♦♦ Mean mark 25%.

BIOLOGY, M5 2021 HSC 10 MC

Cystic fibrosis is an autosomal recessive disorder caused by mutations in the CFTR gene. Many different recessive alleles cause cystic fibrosis.

The four most common alleles of the CFTR gene and their frequencies in the Australian population are shown in the table.
 

\begin{array}{|c|c|}
\hline \rule{0pt}{2.5ex}\quad \quad \textit{Allele} \quad \quad& \ \ \textit{Frequency of allele (%)}\ \ \\
\hline \rule{0pt}{2.5ex}\text{A} \rule[-1ex]{0pt}{0pt}& 98.33 \\
\hline \rule{0pt}{2.5ex}\text{al} \rule[-1ex]{0pt}{0pt}& 1.13 \\
\hline \rule{0pt}{2.5ex}\text{a2}\rule[-1ex]{0pt}{0pt}& 0.08 \\
\hline \rule{0pt}{2.5ex}\text{a3} \rule[-1ex]{0pt}{0pt}& 0.07 \\
\hline
\end{array}

 

What will be the most common genotype of cystic fibrosis patients in Australia?

  1. a1/a1
  2. a1/a2
  3. A/a1
  4. A/A
Show Answers Only

\(A\)

Show Worked Solution
  • A (dominant) where a single copy produces a normal phenotype.
  • a1 and a2 produce cystic fibrosis, with a1 having the highest frequency.
  • Most likely genotype of cystic fibrosis patient is a1/a1.

\(\Rightarrow A\)


♦♦♦ Mean mark 22%.

Calculus, MET2 2020 VCAA 5

Let  `f: R to R, \ f(x)=x^{3}-x`.

Let  `g_{a}: R to R`  be the function representing the tangent to the graph of `f` at  `x=a`, where  `a in R`.

Let `(b, 0)` be the `x`-intercept of the graph of `g_{a}`.

  1. Show that  `b= {2a^{3}}/{3 a^{2}-1}`.   (3 marks)

  2. State the values of `a` for which `b` does not exist.    (1 mark)

  3. State the nature of the graph of `g_a` when `b` does not exist.   (1 mark)

  4. i.  State all values of `a` for which  `b=1.1`. Give your answer correct to four decimal places.   (1 mark)

  5. ii. The graph of `f` has an `x`-intercept at (1, 0).
  6.      State the values of  `a`  for which  `1 <= b <= 1.1`.
  7.      Give your answers correct to three decimal places.   (1 mark)

The coordinate `(b, 0)` is the horizontal axis intercept of `g_a`.

Let `g_b` be the function representing the tangent to the graph of `f` at  `x=b`, as shown in the graph below.
 
 
     
 

  1. Find the values of `a` for which the graphs of `g_a` and `g_b`, where `b` exists, are parallel and where  `b!=a`.   (3 marks)

Let  `p:R rarr R, \ p(x)=x^(3)+wx`, where  `w in R`.

  1. Show that  `p(-x)=-p(x)`  for all  `w in R`.   (1 mark)

A property of the graphs of `p` is that two distinct parallel tangents will always occur at `(t, p(t))` and `(-t,p(-t))` for all  `t!=0`.

  1. Find all values of `w` such that a tangent to the graph of `p` at `(t, p(t))`, for some  `t > 0`, will have an `x`-intercept at `(-t, 0)`.   (1 mark)

  2. Let  `T:R^(2)rarrR^(2),T([[x],[y]])=[[m,0],[0,n]][[x],[y]]+[[h],[k]]`, where  `m,n in R text(\{0})`  and  `h,k in R`.
     
    State any restrictions on the values of `m`, `n`, `h`, and `k`, given that the image of `p` under the transformation `T` always has the property that parallel tangents occur at  `x = -t`  and  `x = t`  for all  `t!=0`.   (1 mark)

Show Answers Only
  1. `text(See Worked Solutions.)`
  2. `a=+-sqrt3/3`
  3. `text(Horizontal line.)`
  4.  i. `a=-0.5052, 0.8084, 1.3468`
  5. ii. `a in (-0.505,-0.500]uu(0.808,1.347)`
  6. `a=+- sqrt5/5`
  7. `text(See Worked Solutions.)`
  8. `w=-5t^2`
  9. `h=0`
Show Worked Solution

a.   `f^{prime}(a) = 3a^2-1`

`g_a(x)\ \ text(has gradient)\ \ 3a^2-1\ \ text(and passes through)\ \ (a, a^3-a)`

`g_a(x)-(a^3-a)` `=(3a^2- 1)(x-a)`  
`g_a(x)` `=(3a^2-1)(x-a)+a^3-a`  

  
`x^{primeprime}-text(intercept occurs at)\ (b,0):`

`0=(3a^2-1)(b-a) + a^3-a`

`(3a^2-1)(b-a)` `=a-a^3`  
`3a^2b-3a^3-b+a` `=a-a^3`  
`b(3a^2-1)` `=a-a^3+3a^3-a`  
`:.b` `=(2a^3)/(3a^2-1)`  

 
b.   `b\ text{does not exist when:}`

♦ Mean mark part (b) 46%.

`(3a^2-1)=0`

`a=+-sqrt3/3`

♦♦ Mean mark part (c) 23%.
 

c.   `text{If}\ \ a=+-sqrt3/3,\ \ g_a^{prime}(x) = 0`

`=>\ text{the graph is a horizontal line (does not cross the}\ xtext{-axis).}`
 

d.i.  `text(Solve)\ {2a^{3}}/{3 a^{2}-1}=1.1\ text(for)\ a:`

`a=-0.5052\ text(or )\ =0.8084\ text(or)\ a=1.3468\ \ text{(to 4 d.p.)}`
  

d.ii.  `text(Solve)\ 1 <= (2a^(3))/(3a^(2)-1) < 1.1\ text(for)\ a:`

♦♦♦ Mean mark part (d)(ii) 13%.

`a in (-0.505,-0.500]uu(0.808,1.347)\ \ text{(to 3 d.p.)}`
 

e.   `f^{prime}(b) = 3b^2-1`

`g_b(x)\ \ text(has gradient)\ \ 3b^2-1\ \ text(and passes through)\ \ (b, b^3-b)`

`g_b(x)-(b^3-b)` `=(3b^2-1)(x-b)`  
`g_b(x)` `=(3b^2-1)(x-b)+b^3-b`  

 
`g_a(x)\ text{||}\ g_b(x)\ \ text{when}`

♦♦♦ Mean mark part (e) 13%.
`3a^2-1` `=3b^2-1`  
  `=3 cdot((2a^3)/(3a^2-1))-1`  

 
`=> a=+-1, +- sqrt5/5, 0`

`text(Test each solution so that)\ \ b!=a :`

`text(When)\ \ a=+-1, 0 \ => \ b=a`

`:. a=+- sqrt5/5`
 

f.    `p(-x)` `=(-x)^3-wx`
    `=-x^3-wx`
    `=-(x^3+wx)`
    `=-p(x)`

 
g.  `p^{prime}(t) = 3t^2+w`

♦♦♦ Mean mark part (g) 3%.

`p(t)\ \ text(has gradient)\ \ 3t^2+w\ \ text(and passes through)\ \ (t, t^3+wt)`

`p(t)-(t^3+wt)` `=(3t^2+w)(x-t)`  
`p(t)` `=(3t^2+w)(x-t) + t^3+wt`  

 
`text{If}\ p(t)\ text{passes through}\ \ (-t, 0):`

`0=(3t^2+w)(-2t) + t^3+wt`

`=>w=-5t^2\ \ (t>0)`
 

h.   `text{Property of parallel tangents is retained under transformation}`

♦♦♦ Mean mark part (h) 2%.

`text{if rotational symmetry remains (odd function).}`

`=>h=0`

`text(No further restrictions apply to)\ m, n\ \ text{or}\ \ k.`

NETWORKS, FUR2 2020 VCAA 5

The Sunny Coast cricket clubroom is undergoing a major works project.

This project involves nine activities: `A` to `I`.

The table below shows the earliest start time (EST) and duration, in months, for each activity.

The immediate predecessor(s) is also shown.

The duration for activity `C` is missing.
 

   

The information in the table above can be used to complete a directed network.

This network will require a dummy activity.

  1. Complete the following sentence by filling in the boxes provided.    (1 mark)

    This dummy activity could be drawn as a directed edge from the end of activity to the start of activity  
  1. What is the duration, in months, of activity  `C`?   (1 mark)

  2. Name the four activities that have a float time.   (1 mark)

  3. The project is to be crashed by reducing the completion time of one activity only.

     

    What is the minimum time, in months, that the project can be completed in?    (1 mark)

Show Answers Only
  1. `B\ text{to the start of activity}\ C.`
  2. `text{2 months}`
  3. `A, E, F, H`
  4. `text{17 months}`
Show Worked Solution

a.   `B\ text{to the start of activity}\ C.`

♦♦ Mean mark part (a) 26%.
   

b.   `text{Sketch network diagram.}`

♦ Mean mark part (b) 49%.

 

`text{Duration of Activity C = 2 months}`
  

c.   `text{Critical path:}\   BCDGI`

♦♦ Mean mark part (c) 23%.

`text{Activities with a float time are activities}`

`text{not on critical path.}`

`:. \ text{Four activities are:}\ \ A, E, F, H`
  

d.   `text{Completion time of}\ BCDGI = 20\ text{months}`

♦♦♦ Mean mark part (d) 12%.

`text{Reduce the completion of}\ B\ text{by 3 months to create}`

`text{a new minimum completion time of 17 months.}`

Statistics, MET2 2020 VCAA 3

A transport company has detailed records of all its deliveries. The number of minutes a delivery is made before or after its schedule delivery time can be modelled as a normally distributed random variable, `T`, with a mean of zero and a standard deviation of four minutes. A graph of the probability distribution of `T` is shown below.
 

  1. If  `"Pr"(T <= a)=0.6`, find `a` to the nearest minute.   (1 mark)

  2. Find the probability, correct to three decimal places, of a delivery being no later than three minutes after its scheduled delivery time, given that it arrives after its scheduled delivery time.   (2 marks)

  3. Using the model described above, the transport company can make 46.48% of its deliveries over the interval  `-3 <= t <= 2`.
  4. It has an improved delivery model with a mean of `k` and a standard deviation of four minutes.
  5. Find the values of `k`, correct to one decimal place, so that 46.48% of the transport company's deliveries can be made over the interval  `-4.5 <= t <= 0.5`   (3 marks)

A rival transport company claims that there is a 0.85 probability that each delivery it makes will arrive on time or earlier.

Assume that whether each delivery is on time or earlier is independent of other deliveries.

  1. Assuming that the rival company's claim is true, find the probability that on a day in which the rival company makes eight deliveries, fewer than half of them arrive on time or earlier. Give your answer correct to three decimal places.   (2 marks)

  2. Assuming that the rival company's claim is true, consider a day in which it makes `n` deliveries.
    1. Express, in terms of `n`, the probability that one or more deliveries will not arrive on time or earlier.   (1 mark)

    2. Hence, or otherwise, find the minimum value of `n` such that there is at least a 0.95 probability that one or more deliveries will not arrive on time or earlier.   (1 mark)
  3. An analyst from a government department believes the rival transport company's claim is only true for deliveries made before 4 pm. For deliveries made after 4 pm, the analyst believes the probability of a delivery arriving on time or earlier is `x`, where  `0.3 <=x <= 0.7`
  4. After observing a large number of the rival transport company's deliveries, the analyst believes that the overall probability that a delivery arrives on time or earlier is actually 0.75
  5. Let the probability that a delivery is made after 4 pm be `y`.
  6. Assuming that the analyst's belief are true, find the minimum and maximum values of `y`.   (2 marks)

Show Answers Only

  1. `a= 1\ text(minute)`
  2. `0.547`
  3. `k=-1.5, -2.5`
  4. `0.003`
  5.  i. `1-0.85^n`
  6. ii. `19`
  7. `2/3`

Show Worked Solution

a.   `T\ ~\ N(0, 4^2)`

`text(Solve (by CAS): Pr)(T<=a) = 0.6`

`:. a= 1\ text(minute)`
 

b.    `text{Pr}(T <= 3∣T > 0)` `=(text{Pr}(0 < T <= 3))/(text{Pr}(T > 0))`
    `=(0.27337 dots)/(0.5)`
    `=0.547\ \ text{(to 3 d.p.)}`

 

c.   `text(Given)\ \ text{Pr}(-3 <= T <= 2) = 0.4648`

`sigma = 4 text{minutes}`

`=> \ text{Pr}(-4.5 <= T – 1.5 <= 0.5) = 0.4648`

`=> k=-1.5`

`text(By symmetry of the normal distribution)`

`text{Pr}(-2 <= T <= 3) = text{Pr}(-3 <= T <= 2) = 0.4648`

`=> \ text{Pr}(-4.5 <= T – 2.5 <= 0.5) = 0.4648`

`=> k=-2.5`

`:. k=-1.5, -2.5`

 

d.   `text{Let}\ \ X\ ~\ text{Bi}(8, 0.85)`

`text(Solve (by CAS):)`

`text{Pr}(X<=3) = 0.003\ \ text{(to 3 d.p.)}`
 

e.i.   `text{Pr(at least 1 delivery is late)}`

`= 1-\ text{Pr(all deliveries are on time)}`

`=1-0.85^n`
 

e.ii.   `text{Solve for}\ n:`

`1-0.85^n` `<0.95`  
`n` `>18.43…`  

 
`:.n_min=19`
 

f.   `text{Pr(delivery made after 4pm)} = y`

`=>\ text{Pr(delivery made before 4pm)} = 1-y`

`0.85(1-y)+xy` `=0.75`  
`y` `=-(0.1)/(x-0.85)`  
  `=(2)/(17-20 x)`  

 
`text(Given ) 0.3<=x<=0.7:`

`y_min = (2)/(17-20 xx 0.3) = 2/11`

`y_max = (2)/(17-20 xx 0.7) = 2/3`

GEOMETRY, FUR2 2020 VCAA 3

Khaleda manufacturers the face cream in Dhaka, Bangladesh.

Dhaka is located at latitude 24° N and longitude 90° E.

Assume that the radius of Earth is 6400 km.

  1. Write a calculation that shows that the radius of the small circle of Earth at latitude 24° N is 5847 km, rounded to the nearest kilometre.   (1 mark)

Khaleda receives an order from Abu Dhabi, United Arab Emirates (24° N, 54° E).

  1. Find the shortest small circle distance between Dhaka and Abu Dhabi.
  2. Round your answer to the nearest kilometre.   (1 mark)

Khaleda sends the order by plane from Dhaka (24° N, 90° E) to Abu Dhabi (24° N, 54° E).

The flight departs Dhaka at 1.00 pm and arrives in Abu Dhabi 11 hours later.

The time difference between Dhaka and Abu Dhabi is two hours.

  1. What time did the flight arrive in Abu Dhabi?   (1 mark)

A helicopter takes the order from the airport to the customer's hotel.

The hotel is 27 km south and 109 km east of the airport.

  1. Show that the bearing of the hotel from the airport is 104°, correct to the nearest degree.   (1 mark)
  2. After the delivery to the hotel, the helicopter returns to its hangar.
  3. The hangar is located due south of the airport.
  4. The helicopter flies directly from the hotel to the hangar on a bearing of 282° .
  5. How far south of the airport is the hangar?
  6. Round your answer to the nearest kilometre.   (1 mark)

Show Answers Only
  1. `text{See Worked Solution}`
  2. `3674 \ text{km}`
  3. `10:00 \ text{pm}`
  4. `text{See Worked Solution}`
  5. `4 \ text{km}`
Show Worked Solution

a.   `text(Let)\ \ r= \ text(radius of small circle)`
 

`cos \ 24^@` `= r/6400`
`r` `=6400 xx cos 24^@`
  `= 5846.69 …`
  `=5847 \ text{(nearest km)}`

 

b.   `text{Small circle through Dhaka and Abu Dhabi has radius of 5847 km.}`

`text{Longitudinal difference}` `= 90 – 54`
  `= 36^@`

 

`:. \ text{Shortest distance}` `= 36/360 xx 2 xx pi xx 5847`
  `= 3673.77 …`
  `= 3674 \ text{km (nearest km)}`

 

c.   `text{Dhaka} \ (24^@ text{N}, 90^@ \ text{E}) \ text{is further east than Abu Dhabi} \  (24^@ text{N}, 54^@ \ text{E})`

`=> \ text{Dhaka is 2 hours ahead.}`

`:. \ text{Flight arrival time (Abu Dhabi time)}`

`= 1:00 \ text{pm} + 11 \ text{hours} – 2 \ text{hours}`

`= 10:00 \ text{pm}`

 

d.

`tan theta` `= 109/27`
`theta` `=tan^(-1) (109/27) = 76.1^@`

  
`:.\ text{Bearing of hotel from airport}`

`=180 – 76.1`

`=104^@\ \ text{(nearest degree)}`

 

e.

`text{Let X = position of hangar}`

`text{Find OX:}`

`tan 12^@` `= text{OX}/109`
`text{OX}` `= 109 xx tan 12^@`
  `= 23.17 \ text{km}`

 

`:. \ text{AX (distance hangar is south of airport)}`

`= 27 – 23.17`

`= 4 \ text{km (nearest km)}`

GEOMETRY, FUR2 2020 VCAA 2

Khaleda has designed a logo for her business.

The logo contains two identical equilateral triangles,

The side length of each triangle is 4.8 cm, shown in the diagram below.
 

  1. Write a calculation to show that the area of one of the triangles, rounded to the nearest centimetre, is 10 cm2.   (1 mark)

In the logo, the two triangles overlap, as shown below. Part of the logo is shaded and part of the logo is not shaded.
 

  1. What is the area of the entire logo?
  2. Round your answer to the nearest square centimetre.   (1 mark)
  3. What is the ratio of the area of the shaded region to the area of the non-shaded region of the logo?   (1 mark)
  4. The logo is enlarged and printed on the boxes for shipping.
  5. The enlarged logo and the original logo are similar shape.
  6. The area of the enlarged logo is four times the area of the original logo.
  7. What is the height, in centimetres, of the enlarged logo?   (1 mark)

Show Answers Only
  1. `10 \ text{cm}^2 \ (text{nearest cm}^2)`
  2. `15 \ text{cm}^2`
  3. `1:2`
  4. `9.6 \ text{cm}`
Show Worked Solution

a.    `text{Triangle is equilateral (all angles = 60}^@)`

`text{Using the sine rule:}`

`A` `= 1/2 a b sin c`
  `= 1/2 xx 4.8 xx 4.8 xx sin 60^@`
  `= 9.976 …`
  `= 10 text{cm}^2 (text{nearest cm}^2)`

♦♦ Mean mark part (b) 32%.

 

b.   `text{L} text{ogo is made up of 2 identical triangles.}`

`text{Divide each triangle into 4 equal smaller triangles.}`

`text{Total shading = 2 small triangles}\ = 1/2 xx \ text{area of 1 triangle}`

`:. \ text{Area of logo}`

`= 2 xx 10 – 1/2 xx 10`

`= 15 \ text{cm}^2`

♦ Mean mark part (c) 48%.

 

c.    `text{Shaded region}` `: \ text{non-shaded}`
  `text{2 triangles}` `: 4 \ text{triangles}`
  `1` `: 2`

 

d.   `text{Area scale factor = 4 (given)}`

♦♦♦ Mean mark part (d) 17%.

`text{Length scale factor} = sqrt4 = 2`
 

`:. \ text{Height of enlarged logo}`

`= 2 xx \ text{height of original logo}`

`= 2 xx 4.8`

`= 9.6 \ text{cm}`

Calculus, MET2 2020 VCAA 2

An area of parkland has a river running through it, as shown below. The river is shown shaded.

The north bank of the river is modelled by the function  `f_(1):[0,200]rarr R, \ f_(1)(x)=20 cos((pi x)/(100))+40`.

The south bank of the river is modelled by the function  `f_(2):[0,200]rarr R, \ f_(2)(x)=20 cos((pi x)/(100))+30`.

The horizontal axis points east and the vertical axis points north.

All distances are measured in metres.
 

A swimmer always starts at point `P`, which has coordinates  (50, 30).

Assume that no movement of water in the river affects the motion or path of the swimmer, which is always a straight line.

  1. The swimmer swims north from point `P`.
  2. Find the distance, in metres, that the swimmer needs to swim to get to get to the north bank of the river.   (1 mark)

  3. The swimmer swims east from point `P`.
  4. Find the distance, in metres, that the swimmer needs to swim to get to the north bank of the river.   (2 marks)

  5. On another occasion, the swimmer swims the minimum distance from point `P` to the north bank of the river.
  6. Find this minimum distance. Give your answer in metres, correct to one decimal place.   (2 marks)

  7. Calculate the surface area of the section of the river shown on the graph in square metres.   (1 mark)

  8. A horizontal line is drawn through point `P`. The section of the river that is south of the line is declared a no "no swimming" zone.
  9. Find the area of the "no swimming" zone, correct to the nearest square metre.   (3 marks)

  10. Scientists observe that the north bank of the river is changing over time. It is moving further north from its current position. They model its predicted new location using the function with rule  `y=kf_(1)(x)`, where `k >= 1`.
  11. Find the values of  `k` for which the distance north across the river, for all parts of the river, is strictly less than 20 m.   (2 marks)

Show Answers Only
  1. `10\ text{m}`
  2. `16 2/3\ text{m}`
  3. `8.5\ text{m}`
  4. `2000\ text{m}^2`
  5. `837\ text{m²}`
  6. `k in [1, 7/6)`
Show Worked Solution

a.   `text{Since swimmer swims due north,}`

`text{Distance}\ = 40-30=10\ text{m}`

 

b.  `text{Solve} \ f_(1)(x)=30 \ text{or} \ x in[50,100]`

`=> x=200/3`

`:.\ text{Distance to swim (east) to reach north bank}`

`=200/3-50`

`=16 2/3\ text{m}`
 

c.   `text{Let swimmer arrive at north bank at the point}\ \ (x,f_(1)(x))`

`text{By Pythagoras,}`

♦ Mean mark part (c) 39%.

`d(x)=sqrt((x-50)^(2)+(f_(1)(x)-30)^(2))`

`text{Solve} \ d/dx(d(x))=0 \ text{for} \ x:`

`x=54.47…`

`:. d_min=8.5\ text{m (to 1 d.p.)}`

 

d.   `text{Shaded Area}`

`=int_(0)^(200)(f_(1)(x)-f_(2)(x))\ dx`

`=2000\ text{m}^2`

 

e.   `text{Find}\ \ f_(1)(x) = 30 \ text{for} x in [50,150]:`

♦♦ Mean mark part (e) 35%.

`=>x=200/3, 400/3`

`text{Find}\ \ f_(2)(x) = 30 \ text{for} \ x in [50,150]:`

`=>x=50, 150`

`:.\ text{Area}` `=int_(50)^(150)(30-f_(2)(x))\ dx-int_((200)/(3))^((400)/(3))(30-f_(1)(x))\ dx`  
  `=837\ text{m² (to nearest m²)}`  

♦♦♦Mean mark part (f) 15%.

 

f.   `text{Let}\ \ D(x)=\ text{vertical distance between banks}`

`D(x)` `=kf_(1)(x)-f_(2)(x)`  
  `=20k cos((pi x)/(100))+40k-(20 cos((pi x)/(100))+30)`   
  `=(20k-20)cos((pi x)/(100)) +40k-30`  

  
`text{Given}\ \ D(x)<20 \ text{for}\ x in[0,200]`

`text{Maximum} \ cos((pi x)/(100)) = 1\  text{when}\ \ x=0, 200`

`text{Solve} \ 20k-20+40k-30<20\ \ text{for}\ k:`

`=> k<7/6`

`:. k in [1,7/6)`

GRAPHS, FUR2 2020 VCAA 4

Another section of Kyla's business services and details cars and trucks.

Every vehicle is both serviced and detailed.

Each car takes two hours to service and one hour to detail.

Each truck takes three hours to service and three hours to detail.

Let `x` represent the number of cars that are serviced and detailed each day.

Let `y` represent the number of trucks that are serviced and detailed each day.

Past records suggest there are constraints on the servicing and detailing of vehicles each day.

These constraints are represented by Inequalities 1 to 4 below.

`text{Inequality 1}`   `x >= 16`    
`text{Inequality 2}`   `y >= 10`    
`text{Inequality 3}`   `2x + 3y <= 96`   `text{(servicing department)}`
`text{Inequality 4}`   `x + 3y <= 72`   `text{(detailing department)}`
     
  1. Explain the meaning of Inequality 1 in the context of this problem.   (1 mark)
  2. Each employee at the business works eight hours per day.
  3. What is the maximum number of employees who can work in the servicing department each day?   (1 mark)

The graph below shows the feasible region (shaded) that satisfies Inequalities 1 to 4 .
 


 

  1. On a day when 20 cars are serviced and detailed, what is the maximum number of trucks that can be serviced and detailed?   (1 mark)
  2. When servicing and detailing, the business makes a profit of $150 per car and $225 per truck.
  3. List the points within the feasible region that will result in a maximum profit for the day.   (2 marks)

Show Answers Only
  1. `text{At least 16 cars are serviced and detailed each day.}`
  2. `12`
  3. `17 \ text{trucks}`
  4. `(24, 16),(27, 14),(30, 12), \ text{and} (33, 10)`
Show Worked Solution

a.   `text{At least 16 cars are serviced and detailed each day.}`

♦♦ Mean mark part (b) 34%.

 

b.   `text{Consider Inequality 3:} \ 2x + 3y ≤ 96`

`text{Total time} \ ≤ 96 \ text{hours and each employee works 8 hours.}`

`:. \ text{Maximum employees in servicing}`

`=96/8`

`=12`
 

c.    `text{Find} \ y_text{max} \ text{when} \ x= 20`

♦ Mean mark part (c) 42%.

`text{With reference to the feasible region,}`

`y_text{max} \ text{lies on the line of Inequality 4}`

`x + 3y` `= 72`
`20 + 3y` `= 72`
`3y`  `= 52`
`y` `= 17.33`

 
`:. y_text{max} = 17 \ text{trucks (highest integer within the feasible region)}`

 

d.    `text{Profits: $150 per car, $225 per truck}`

♦♦♦ Mean mark part (d) 19%.

`P = 150x + 225y`

`=> \ m_P = – 150/225 = – 2/3`

`text{The objective function} \ (P) \ text{is parallel to}\ \ 2x+3y=96\ \ text{(Inequality 3)}`
 


 

`=> text{Maximum profit occurs at integer co-ordinates on line} \ AB.`

`A\ text(occurs at intersection of:)`

`2x+3y=96 and x+3y=72\ \ =>\ \ x=24`

`B\ text(occurs at intersection of:)`

`2x+3y=96 and y=10\ \ =>\ \ x=33`

`text(Max profit requires)\ \ x in [24,33]`

`text{Test each integer}\ xtext{-value for an integer}\ ytext{-value:}`

`:.\ text{Maximum profit occurs at}`

`text{(24, 16), (27, 14), (30, 12) and (33, 10)}`

GRAPHS, FUR1 2020 VCAA 10 MC

The feasible region for a linear programming problem is shaded in the diagram below.

The line through points `A` and `B` is horizontal and the line through points `C` and `D` is vertical.

The equation for the objective function for this problem is of the form

`Z = bx + 4.5y`     where  `b > 0`

The value(s) of  `b`  such that the objective function is maximised only at point  `C`  is

  1. `0 < b < 4.5`
  2. `b > 4.5`
  3. `b = 9`
  4. `0 < b < 9`
  5. `b > 9`
Show Answers Only

`E`

Show Worked Solution

`m_(BC) = (14 – 0)/(0 – 7) = -2`

♦♦ Mean mark 31%.

`text(Objective function maximized at)\ C\ text(only)`

`=>\ text(gradient is)\ < -2`
 

`Z = bx + 4.5y`

`y = -b/4.5x + Z/4.5`

`text{The maximum will occur at}\ C\ text{only if the objective function}`

`text{has the steeper of the two gradients.}`

`-b/4.5` `< -2`
`-b` `< -9`
`b` `> 9`

 
`=>  E`

Graphs, MET2 2020 VCAA 20 MC

Let  `f:R→R, \ f(x)=cos(ax)`, where  `a in R text(\{0})`, be a function with the property

`f(x)=f(x+h),` for all  `h in Z`

Let  `g:D rarr R, \ g(x)=log_(2)(f(x))`  be a function where the range of `g` is `[-1,0]`.

A possible interval for `D` is

  1. `[(1)/(4),(5)/(12)]`
  2. `[1,(7)/(6)]`
  3. `[(5)/(3),2]`
  4. `[-(1)/(3),0]`
  5. `[-(1)/(12),(1)/(4)]`
Show Answers Only

`B`

Show Worked Solution

`f(x)=cos(alpha x)=f(x+h)=cos(a(x+h))`

♦♦♦ Mean mark 18%.

`=>a=2pi`

`g(x)=log_(2)(f(x))=log_(2)(f(x+h))=log_(2)(cos(a(x+h)))`

`-1leqlog_(2)(cos(2pi x))leq0`

`(1)/(2)leq cos(2pi x)leq1`

`text(Sketch) \ y=cos(2pi x)\ \ text(by CAS.)`

`text(By inspection of graph,)\ \ (1)/(2)leq cos(2pi x)leq1\ \text{for}\ x in [1,(7)/(6)]`

`=>B`

Probability, MET2 2020 VCAA 19 MC

Shown below is the graph of `p`, which is the probability function for the number of times, `x`, that a ' 6 ' is rolled on a fair six-sided die in 20 trials.


 

Let `q` be the probability function for the number of times, `w`, that a ' 6 ' is not rolled on a fair six-sided die in 20 trials. `q(w)` is given by

  1. `p(20-w)`
  2. `p(1-(w)/( 20))`
  3. `p((w)/( 20))`
  4. `p(w-20)`
  5. `1-p(w)`
Show Answers Only

`A`

Show Worked Solution

`q∼text(Bi)(20,(5)/(6)),quad p∼text(Bi)(20,(1)/(6))`

♦ Mean mark 45%.

`q(19)=([20],[19])((5)/(6))^(19)((1)/(6))=p(1)=([20],[1])((1)/(6))((5)/(6))^(19)`

`q(18)=([20],[18])((5)/(6))^(18)((1)/(6))^(2)=p(2)=([20],[2])((1)/(6))^(2)((5)/(6))^(18)`

`text(Generally,)`

`g(w)=([20],[w])((5)/(6))^(w)((1)/(6))^(20-w)=p(20-w)=([20],[20-w])((1)/(6))^(20-w)((5)/(6))^(w)`

`q(w)=p(20-w)`

`=>A`

Graphs, MET2 2020 VCAA 13 MC

The transformation  `T:R^(2)rarrR^(2)`  that maps the graph of  `y=cos(x)`  onto the graph of  `y=cos(2x+4)`  is

  1. `T([[x],[y]])=[[(1)/(2),0],[0,1]]([[x],[y]]+[[-4],[0]])`
  2. `T([[x],[y]])=[[(1)/(2),0],[0,1]][[x],[y]]+[[-4],[0]]`
  3. `T([[x],[y]])=[[(1)/(2),0],[0,1]]([[x],[y]]+[[-2],[0]])`
  4. `T([[x],[y]])=[[2,0],[0,1]]([[x],[y]]+[[2],[0]])`
  5. `T([[x],[y]])=[[2,0],[0,1]][[x],[y]]+[[2],[0]]`
Show Answers Only

`A`

Show Worked Solution

`y=cos(2x+4)=cos(2(x+2))`

♦♦♦ Mean mark 26%.

`text{Dilation of factor} \ 1/2 \ text{from} \ y text{-axis}.`

`text{Translation of 2 units to the left.}`
 

`T([[x],[y]])=[[(1)/(2),0],[0,1]][[x],[y]]+[[-2],[0]]=[[(1)/(2),0],[0,1]]([[x],[y]]+[[-4],[0]])`
 

`=>  A`

NETWORKS, FUR1 2020 VCAA 7 MC

Four friends go to an ice-cream shop.

Akiro chooses chocolate and strawberry ice cream.

Doris chooses chocolate and vanilla ice cream.

Gohar chooses vanilla ice cream.

Imani chooses vanilla and lemon ice cream.

This information could be presented as a graph.

Consider the following four statements:

  • The graph would be connected.
  • The graph would be bipartite.
  • The graph would be planar.
  • The graph would be a tree.

How many of these four statements are true?

  1. 0
  2. 1
  3. 2
  4. 3
  5. 4
Show Answers Only

`E`

Show Worked Solution

`text(True statements :)`

♦♦♦ Mean mark 11%.

`text{The graph is connected (a path exists between all vertices).}`

`text{The graph is bipartite (vertices can be divided into two groups).}`

`text{The graph is planar (no edges cross if strawberry is moved to the top).}`

`text{The graph forms a tree (no cycles).}`

`=>  E`

Networks, STD2 N3 SM-Bank 50

Roadworks planned by the local council require 13 activities to be completed.

The network below shows these 13 activities and their completion times in weeks.
 

  1. What is the earliest start time, in weeks, of activity `K`?  (1 mark)

  2. How many of these activities have zero float time?  (2 marks)

  3. It is possible to reduce the completion time for activities `A, E, F, L` and `K`.
  4. The reduction in completion time for each of these five activities will incur an additional cost.
  5. The table below shows the five activities that can have their completion time reduced and the associated weekly cost, in dollars.
     
       
  6. The completion time for each these five activities can be reduced by a maximum of two weeks.
  7. The overall completion time for the roadworks can be reduced to 16 weeks.
  8. What is the minimum cost, in dollars, of this change in completion time?  (3 marks)

Show Answers Only
  1. `14 \ text{weeks}`
  2. `7`
  3. `$ 380 \ 000`
Show Worked Solution

a.    `text{Scan forwards:}`

`EST \ (text{activity} \ K)`

`= A \ E \ J`

`= 6 + 5 + 3`

`= 14 \ text{weeks}`
 

b.     `text{Scan backwards:}`

`text{Critical paths:}\ ADGLM\ text(and)\ AEHLM`

`:. \ text{7 activities have no float time:} \ ADEGHLM`
 

c.    `text{There are 9 possible paths}`

`ADGLM\ (19), AEHLM\ (19) , AEIM\ (14)`

`AEJK\ (17), BCEIM \ (13), BCEJK\ (16)`

`BCEHLM\ (18), BCDGLM \ (18), BFK (11)`

`text{Consider the 5 paths with completions over 16 weeks}`

` to \ text{all contain}\ A\ text{or}\ L \ text{or both.}`
  

`text{Consider} \ ADGLM, AEHLM \ (text{contains both} \ A\ text{and} \ L )`

`to \ text{reduce} \ L xx 2 \ ,  A xx 1 \ text{to reach 16 weeks}`

`to \ text{cheaper than} \ L xx 1 \ , \ A xx 2`
  

`text{Consider} \ BCEHLM , BCDGLM\ (text{both contain} \ L \ text{only})`

`to \ text{reduce} \ L xx 2 \ text{to reach 16 weeks}`
 

`text{Consider} \ AEJK \ ( text{contains} \ A \ text{only} )`

`to \ text{reduce} \ A xx 1 \ text{reach 16 weeks}.`
 

`:. \ text{Minimum cost to reduce time to 16 weeks}`

`= 2 xx 120\ 000 + 1 xx  140\ 000`

`= $ 380\ 000`

GRAPHS, FUR2 2021 VCAA 4

Health and training sessions are held each day at the new community centre.

  • Let `x` be the number of sessions for children each day.
  • Let `y` be the number of sessions for adults each day.
  • The total number of all sessions each day must be at least 10.
  • The number of sessions for adults must not be less than the number of sessions for children.
  • It takes 30 minutes for each session for children and 40 minutes for each session for adults.

The constraints on the health and training sessions each day can be represented by the following five inequalities.

Inequality 1      `x >= 0`

Inequality 2      `y >= 0`

Inequality 3      `x + y >= 10`

Inequality 4       `y >= x`

Inequality 5        `30x + 40y <= 600`

  1. Explain the meaning of Inequality 5 in the context of this situation.  (1 mark)

The graph below shows the feasible region (shaded) that satisfies Inequality 1 to 5.

  1. What is the maximum number of sessions for children each day?  (1 mark)
  2. The community profits from these sessions.
  3. Each session for children makes a profit of $45 and each session for adults makes a profit of $60.
  4.  i.  Determine the maximum profit per day from all health and training sessions. (1 mark)
  5. ii. List all the points within the feasible region that result in this maximum profit. (1 mark)
Show Answers Only
  1. `text{The time of all adult and children sessions each day, in total,}`
    `text{must be less than 600 minutes (10 hours).}`
  2. `8`
  3.  i.  `$900`
    ii. `(0, 15), (4, 12) and (8, 9)`
Show Worked Solution

a.    `text{The time of all adult and children sessions each day, in total,}`

`text{must be less than 600 minutes (10 hours).}`
 

b.    `text{Maximum children sessions = 8}`

`text{(largest integer value of} \ x \ text{in the feasible region)}`
 

c.i.  `P = 45 x + 60 y`

`y = – 3/4 x + P/60`

`text{Objective function’s gradient is the same as} \ 30x + 40y = 600`

`=> \ text{maximum profit occurs at integer points on graph of}`

 `30x+40y=600\ \ text{in feasible region.}`
 

`text{Using (0, 15):}`

`P_text{max}` `= 45 xx 0 + 60 xx 15`
  `= $900`

 

c.ii.

 

`P_text{max} \ text{occurs at (0, 15), (4, 12) and (8, 9)}`

Statistics, SPEC2 2021 VCAA 6

The maximum load of a lift in a chocolate company's office building is 1000 kg. The masses of the employees who use the lift are normally distributed with a mean of 75 kg and a standard deviation of 8 kg. On a particular morning there are `n` employees about to use the lift.

  1. What is the maximum possible value of `n` for there to be less than a 1% chance of the lift exceeding the maximum load?   (2 marks)

Clare, who is one of the employees, likes to have a hot drink after she exits the lift. The time taken for the drink machine to dispense a hot drink is normally distributed with a mean of 2 minutes and a standard deviation of 0.5 minutes. Times taken to dispense successive hot drinks are independent.

  1. Clare has a meeting at 9.00 am and at 8.52 am she is fourth in the queue for a hot drink. Assume that the waiting time between hot drinks dispensed is negligible and that it takes Clare 0.5 minutes to get from the drink machine to the meeting room.
  2. What is the probability, correct to four decimal places, that Clare will get to her meeting on time?   (2 marks)

Clare is a statistician for the chocolate company. The number of chocolate bars sold daily is normally distributed with a mean of 60 000 and a standard deviation of 5000. To increase sales, the company decides to run an advertising campaign. After the campaign, the mean daily sales from 14 randomly selected days was found to be 63 500.

Clare has been asked to investigate whether the advertising campaign was effective, so she decides to perform a one-sided statistical test at the 1% level of significance.

  1.   i. Write down suitable null and alternative hypotheses for this test.   (1 mark)

  2.  ii. Determine the `p` value, correct for decimal places, for this test.   (1 mark)

  3. iii. Giving a reason, state whether there is any evidence for the success of the advertising campaign.   (1 mark)

  4. Find the range of values for the mean daily sales of another 14 randomly selected days that would lead to the null hypothesis being rejected when tested at the 1% level of significance. Give your answer correct to the nearest integer.   (1 mark)

  5. The advertising campaign has been successful to the extent that the mean daily sales is now 63 000.
  6. A statistical test is applied at the 5% level of significance.
  7. Find the probability that the null hypothesis would be incorrectly accepted, based on the sales of another 14 randomly selected days and assuming a standard deviation of 5000. Give your answer correct to three decimal places.   (2 marks)

Show Answers Only
  1. `12`
  2. `0.3085`
  3.   i. `H_0: \ mu = 60 \ 000, \ H_1: \ mu > 60 \ 000`
  4.  ii.  `0.0044`
  5. iii.  `text{Successful as} \ p text{-value is below 0.01.}`
  6. `n ≥ 63\ 109`
  7. `0.274`
Show Worked Solution

a.    `text{Method 1}`

♦♦ Mean mark 22%.

`text{Let} \ \ M_i\ ~\ N (75, 8^2) \ \text{for} \ \ i = 1, 2, 3, … , n`

`W_n = W_1 + W_2 + … + W_n`

`E (W_n) = E(M_1 + … + M_n) = 75n`

`text(s.d.) (W_n) = text{s.d.} (M_1 + … M_n) = 8 sqrtn`

`W_n\ ~\ N (75n, 8^2 n)`

`text{Using} \ Z\ ~\ N (0, 1)`

`text(Pr) (W_n > 1000) = 0.01`

`text(Pr) (Z > {1000-75 n}/{8 sqrtn}) = 0.01`
 
`n = 12.5`

`:. \ text{Largest} \ n = 12`
 

`text{Method 2}`

`text{By trial and error}`
 
`text(Pr) (M_1 + … + M_11 > 1000) ≈ 0`

`text(Pr) (M_1 + … + M_12 > 1000) ≈ 0.0002`

`text(Pr) (M_1 + … + M_13 > 1000) ≈ 0.193`

`:. \ text{Largest} \ n = 12`

 

b.   `T_i\ ~\ N (2, 0.5^2) \ \ text{for} \ \ i = 1, 2, …`

Mean mark part (b) 51%.

`text{Wait time} \ (T) = T_1 + T_2 + T_3 + T_4`

`E(T) = 4 xx 2 = 8`

`text{s.d.}(T) = text{s.d.}(T_1 + T_2 + T_3 + T_4) = sqrt4 xx 0.5 = 1`
 
`T\ ~\ N (8, 1)`

`text(Pr) (T < 7.5) = 0.3085`

`text{By CAS: normCdf} (0, 7.5, 8, 1)`

 

c.i.  `H_0: \ mu = 60 \ 000`

`H_1: \ mu > 60 \ 000`
 

c.ii.  `text(Pr) (barX > 63\ 500 | mu = 60 \ 000) = 0.004407`

  `:. \ p \ text{value} = 0.0044`

 `text{By CAS: norm Cdf} (63\ 500, oo, 60\ 000, 5000/sqrt14)`
 

c.iii.  `text{S} text{ince the} \ p text{-value is below 0.01, there is strong evidence}`

   `text{the advertising was effective (against the null hypothesis).}`

 

d.   `text(Pr) (barX > n | mu = 60 \ 000) < 0.01`

♦♦♦ Mean mark part (d) 16%.

`n ≥ 63\ 109`

`text{By CAS: inv Norm} (0.99, 60 \ 000, 5000/sqrt14)`

 

e.    `text{Similar to part (d):}`

♦♦♦ Mean mark part (e) 10%.

`text(Pr) (barX > n | mu = 60 \  000) < 0.05`

`n ≤ 62198`

`text{By CAS: invNorm} \ (0.95, 60 \ 000, 5000/sqrt14)`
 
`text{If} \ \ mu = 63\ 000, text{find probability null hypothesis incorrectly accepted:}`

`text(Pr) (barX < 62\ 198 | mu = 63\ 000) = 0.274`

`text{By CAS: normCdf} (0, 62\ 198, 63\ 000, 5000/sqrt14)`


NETWORKS, FUR2 2021 VCAA 4

Roadworks planned by the local council require 13 activities to be completed.

The network below shows these 13 activities and their completion times in weeks.
 

  1. What is the earliest start time, in weeks, of activity `K`?   (1 mark)

  2. How many of these activities have zero float time?   (1 mark)

  3. It is possible to reduce the completion time for activities `A, E, F, L` and `K`.
  4. The reduction in completion time for each of these five activities will incur an additional cost.
  5. The table below shows the five activities that can have their completion time reduced and the associated weekly cost, in dollars.
     
       
  6. The completion time for each these five activities can be reduced by a maximum of two weeks.
  7. The overall completion time for the roadworks can be reduced to 16 weeks.
  8. What is the minimum cost, in dollars, of this change in completion time?   (1 mark)

Show Answers Only
  1. `14 \ text{weeks}`
  2. `7`
  3. `$ 380 \ 000`
Show Worked Solution

a.    `text{Scan forwards:}`

`EST \ (text{activity} \ K)`

`= A \ E \ J`

`= 6 + 5 + 3`

`= 14 \ text{weeks}`
 

b.     `text{Scan backwards:}`

`text{Critical paths:}\ ADGLM\ text(and)\ AEHLM`

`:. \ text{7 activities have no float time:} \ ADEGHLM`
 

c.    `text{There are 9 possible paths}`

`ADGLM\ (19), AEHLM\ (19) , AEIM\ (14)`

`AEJK\ (17), BCEIM \ (13), BCEJK\ (16)`

`BCEHLM\ (18), BCDGLM \ (18), BFK (11)`

`text{Consider the 5 paths with completions over 16 weeks}`

` to \ text{all contain}\ A\ text{or}\ L \ text{or both.}`
  

`text{Consider} \ ADGLM, AEHLM \ (text{contains both} \ A\ text{and} \ L )`

`to \ text{reduce} \ L xx 2 \ ,  A xx 1 \ text{to reach 16 weeks}`

`to \ text{cheaper than} \ L xx 1 \ , \ A xx 2`
  

`text{Consider} \ BCEHLM , BCDGLM\ (text{both contain} \ L \ text{only})`

`to \ text{reduce} \ L xx 2 \ text{to reach 16 weeks}`
 

`text{Consider} \ AEJK \ ( text{contains} \ A \ text{only} )`

`to \ text{reduce} \ A xx 1 \ text{reach 16 weeks}.`
 

`:. \ text{Minimum cost to reduce time to 16 weeks}`

`= 2 xx 120\ 000 + 1 xx  140\ 000`

`= $ 380\ 000`