Four triangular shaped playgrounds are shown below.
Which of these play grounds has the least surface area?
|
|
|
|
|
|
|
|
|
|
|
Aussie Maths & Science Teachers: Save your time with SmarterEd
Four triangular shaped playgrounds are shown below.
Which of these play grounds has the least surface area?
|
|
|
|
|
|
|
|
|
|
|
`text(Check each option:)`
`text(Option 1 -)\ \ 1/2 xx 34 xx 15 = 255\ text(m)^2`
`text(Option 2 -)\ \ 1/2 xx 20 xx 26 = 260\ text(m)^2`
`text(Option 3 -)\ \ 1/2 xx40 xx 18 = 360\ text(m)^2`
`text(Option 4 -)\ \ 1/2 xx28 xx 25 = 350\ text(m)^2`
`:.\ text(The backyard with the least area is:`
In a suburb, four families measured the dimensions of their rectangular backyards.
Which backyard has the largest area?
|
|
|
|
|
|
|
|
|
|
|
`text(Checking each option:)`
`text(Option 1:)\ 11 xx 18 = 198 text(m)^2`
`text(Option 2:)\ 16 xx 6 = 96 text(m)^2`
`text(Option 3:)\ 15 xx 10 = 150 text(m)^2`
`text(Option 4:)\ 14 xx 12 = 168 text(m)^2`
`:. text(The backyard with the largest area is the)\ 11\ text(m) xx 18\ text(m)`
`text(with a total area of 198 square metres.)`
A store sells second hand mobile phones.
The graph below shows the price of 2 similar second-hand phones.
Which of the following is true based on the graph shown?
|
|
Phone A is older and less expensive than Phone B |
|
|
Phone B is older and more expensive than phone A |
|
|
Phone A is newer and more expensive than Phone B |
|
|
Phone A is older and more expensive than Phone B |
`text(Phone A is newer and more expensive than Phone B)`
`text(Phone A is left of Phone B → it is newer.)`
`text(Phone A is higher than Phone B → it is more expensive.)`
`:.\ text(Phone A is newer and more expensive than Phone B.)`
A man bought a plot of land in the past and now he is selling it.
The graph marks the price of the land when the man bought it and the price of the land now.
Which of the following is true based on the graph shown?
|
|
The land is less expensive now than when it was purchased. |
|
|
The land is more expensive years ago than now. |
|
|
The land is more expensive now than years ago. |
|
|
The price of the land does not change with time. |
`text(The land is more expensive now than years ago.)`
`text(Z is further right on the x-axis → most recent price.)`
`text(Z is higher on the y-axis → more expensive.)`
`:.\ text(The land is more expensive now than years ago.)`
A circle is divided into 8 equal parts, as shown in the diagram below.
What percentage of the circle’s area has been labelled with even numbers?
|
|
37.5% |
|
|
50% |
|
|
57.5% |
|
|
62.5% |
|
|
70% |
`text(62.5%)`
`text(S)text(ince all areas are equal:)`
| `text(Percentage)` | `= text(Number of even numbers)/text(Total number of sections) xx 100` |
| `= 5/8 xx 100` | |
| `= 62.5text(%)` |
For non-zero constants `a` and `b`, where `b < 0`, the expression `1/(ax(x^2 + b))` in partial fraction form with linear denominators, where `A, B` and `C` are real constants, is
`D`
| `1/(ax(x^2 + b))` | `= 1/a (A_1/x + B_1/(x + sqrt|b|) + C_1/(x – sqrt|b|))` |
| `= A/x + B/(x + sqrt|b|) + C/(x – sqrt|b|)` |
`=>D`
Let `f(x) = sqrt(x - 1)/x` over its implied domain and `g(x) = text(cosec)^2 x` for `0 < x < pi/2`.
The rule for `f(g(x))` and the range, respectively, are given by
`E`
| `f(g(x))` | `= sqrt(text(cosec)^2(x) – 1)/(text(cosec)^2(x))` |
| `= sqrt(cot^2(x))/(text(cosec)^2(x))` | |
| `= (cos(x))/(sin(x)) · sin^2(x)` | |
| `= cos(x)sin(x)` | |
| `= 1/2 sin(2x)` |
`text(Given)\ \ 0 < x < pi/2`,
`text(Range)\ \ f(g(x)) :\ \ (0, 1/2]`
`=>E`
Julian was driving into town and hit a kangaroo `3/4` of a kilometre into his trip.
Which of these represent where Julian hit the kangaroo?
|
|
 |
|
|
 |
|
|
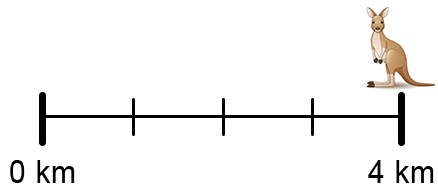 |
|
|
 |

`text(Each spacing is worth)\ 1/4\ text(km.)`

Axe went jogging and stopped after `2/6` of a kilometre to take a rest.
Which of these represents where Axe stopped jogging?
|
|
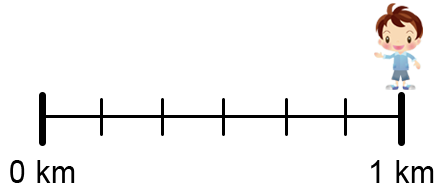 |
|
|
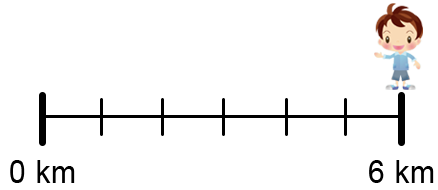 |
|
|
 |
|
|
 |

`text(Each spacing is worth)\ 1/6\ text(km.)`

What number is exactly halfway between `4 frac{1}{4}` and `6 frac{3}{4}`
|
|
`4 frac{3}{4}` | |
|
|
`5` | |
|
|
`5 frac{1}{4}` | |
|
|
`5 frac{1}{2}` |
`5 frac{1}{2}`
| `text{Halfway}` | `= (4 frac{1}{4} + 6 frac{3}{4}) \ div 2` | |
| `= 11/2` | ||
| `= 5 frac{1}{2}` |
The directed network below shows the sequence of activities, `A` to `I`, that is required to complete an office renovation.
The time taken to complete each activity, in weeks, is also shown.
The project manager would like to complete the office renovation in less time.
The project manager asks all the workers assigned to activity `H` to also work on activity `F`.
This will reduce the completion time of activity `F` to three weeks.
The workers assigned to activity `H` cannot work on both activity `H` and activity `F` at the same time.
No other activity times will be changed.
This change to the network will result in a change to the completion time of the office renovation.
Which one of the following is correct?
`A`
`text{Original forward scan (note}\ F\ text{is 6 origionally but}`
`text{is reduced to 3 for the adjusted critical path):}`
`text(Original critical path is:)\ ACEFGI = 2+5+3+6+4+5=25`
`text(If activity)\ F\ text(is completed in 3 weeks, and then)`
`text(activity)\ H\ text(starts, new critical path is:)`
`ACEF\ text{(dummy)}\ HI = 24\ text(weeks)`
`=> A`
The flow of liquid through a series of pipelines, in litres per minute, is shown in the directed network below.
Five cuts labelled A to E are shown on the network.
The number of these cuts with a capacity equal to the maximum flow of liquid from the source to the sink, in litres per minute, is
`C`
`text(Minimum cut) = 33`
`text(Cut)\ A = 8 + 15 + 15 = 38`
`text(Cut)\ B = 8 + 15 + 10 = 33`
`text(Cut)\ C = 15 + 8 + 10 = 33`
`text(Cut)\ D = 15 + 8 + 10 = 33`
`text(Cut)\ E = 15 + 8 + 5 + 10 = 38`
`text{(Note that it is arguable that the flow of 5 should not be counted}`
`text{in Cut}\ E,\ text(making the correct answer)\ D.\ text(This is because this)`
`text{edge cannot hold any flow in the network as given.)}`
`=> C`
Ray deposited $5000 in an investment account earning interest at the rate of 3% per annum, compounding quarterly.
A rule for the balance, `R_n` , in dollars, after `n` years is given by
`E`
`text(Quarterly rate) = 0.03/4 = 0.0075`
`text(Compounding periods) = 4n`
`:.\ text(Balance after)\ n\ text(years)`
`= 5000 xx 1.0075^(4n)`
`=> E`
Part of the graph of `y = f(x)`, where `f:(0, ∞) -> R, \ f(x) = xlog_e(x)`, is shown below.
The graph of `f` has a minimum at the point `Q(a, f(a))`, as shown above.
--- 6 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
--- 7 WORK AREA LINES (style=lined) ---
i. Find the value of `k` for which `y = 2x` is a tangent to the graph of `g`. (1 mark)
--- 6 WORK AREA LINES (style=lined) ---
ii. Find all values of `k` for which the graphs of `g` and `g^(-1)` do not intersect. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
a. `y = xlog_e x`
| `(dy)/(dx)` | `= x · 1/x + log_e x` |
| `= 1 + log_e x` |
`text(Find)\ x\ text(when)\ (dy)/(dx) = 0:`
| `1 + log_e x` | `= 0` |
| `log_e x` | `= -1` |
| `x` | `= 1/e` |
| `y` | `= 1/e log_e (e^(-1))` |
| `= -1/e` |
`:. Q(1/e, -1/e)`
| b. | `int 2x log_e(x) + x\ dx` | `= x^2 log_e (x) + c` |
| `2 int x log_e(x)\ dx` | `= x^2 log_e (x)-intx\ dx + c` | |
| `:. int x log_e(x)\ dx` | `= (x^2 log_e (x))/2-(x^2)/4 \ \ (c = 0)` |
| c. |
`text(When)\ \ x log_e x = 0 \ => \ x = 1`
`=> b = 1`
| `:.\ text(Area)` | `= −int_(1/e)^1 x log_e(x)\ dx` |
| `= [(x^2)/4-(x^2 log_e(x))/2]_(1/e)^1` | |
| `= (1/4-0)-(1/(4e^2)-(log_e(e^(-1)))/(2e^2))` | |
| `= 1/4-(1/(4e^2) + 1/(2e^2))` | |
| `= 1/4-3/(4e^2) \ text(u)^2` |
d.i. `text(When)\ \ f^{prime}(x) = m_text(tang) = 2,`
| `1 + log_e(x)` | `= 2` |
| `x` | `= e` |
`text(T)text(angent meets)\ \ g(x)\ \ text(at)\ \ (e, 2e)`
| `g(e)` | `= f(e) + k` |
| `2e` | `= e log_e e + k` |
| `:.k` | `= e` |
d.ii. `text(Find the value of)\ k\ text(when)\ \ y = x\ \ text(is a tangent to)\ g(x):`
`text(When)\ \ f^{prime}(x) = 1,`
| `1 + log_e(x)` | `= 1` |
| `x` | `= 1` |
`text(T)text(angent occurs at)\ (1, 1)`
`g(1) = f(1) + k \ => \ k = 1`
`:.\ text(Graphs don’t intersect for)\ k ∈ (1, ∞)`
Let `I_n = int_0^(frac{pi}{2}) sin^(2n + 1)(2theta)\ d theta, \ n = 0, 1, ...`
--- 8 WORK AREA LINES (style=lined) ---
--- 8 WORK AREA LINES (style=lined) ---
Let `J_n = int_0^1 x^n (1 - x)^n\ dx , \ n = 0, 1, 2,...`
--- 8 WORK AREA LINES (style=lined) ---
--- 10 WORK AREA LINES (style=lined) ---
i. `text{Prove} \ \ I_n = frac{2n}{2n + 1} I_(n-1) , \ n ≥ 1`
`I_n = int_0^(frac{pi}{2}) sin^(2n) (2 theta) * sin (2 theta)\ d theta`
`text{Integrating by parts:}`
| `u = sin^(2n) (2 theta)` | `u^(′) = 2n sin^(2n -1) (2 theta) xx -frac(1)(2) cos (2 theta)` | |
| `v = -frac{1}{2} cos (2 theta)` | `v^(′) = sin 2 theta` |
| `I_n` | `= [ sin^(2n) (2 theta) * -frac{1}{2} cos (2 theta)]_0^(frac{pi}{2}) -2n int_0^(frac{pi}{2}) sin^(2n -1) (2 theta) * 2 cos (2 theta) * -frac{1}{2} cos (2 theta)\ d theta` |
| `I_n` | `= 0 + 2n int_0^(frac{pi}{2}) sin^(2n-1) (2 theta) * cos^2 (2 theta)\ d theta` |
| `I_n` | `= 2 n int_0^(frac{pi}{2}) sin^(2n-1) (2 theta) (1 – sin^2 (2 theta))\ d theta` |
| `I_n` | `= 2 n int_0^(frac{pi}{2}) sin^(2n-1) ( 2 theta) – sin^(2n+1) (2 theta)\ d theta` |
| `I_n` | `= 2n (I_(n-1) – I_n)` |
| `I_n + 2 n I_n` | `= 2 n I_(n-1)` |
| `I_n (2n + 1)` | `= 2 n I_(n-1)` |
| `therefore I_n` | `= frac{2n}{2n +1} I_(n-1)` |
| ii. | `I_0` | `= int_0^(frac{pi}{2}) sin (2 theta)\ d theta` |
| `= [ -frac(1)(2) cos (2 theta) ]_0^(frac{pi}{2}` | ||
| `=( -frac{1}{2} cos pi + frac{1}{2} cos 0 )` | ||
| `= 1` | ||
| `I_n` | `= frac{2n}{2n + 1} I_(n-1)` |
| `I_(n-1)` | `= frac{2(n -1)}{2n -1} I_(n-2)` |
| `vdots` | |
| `I_1` | `= frac{2}{3} I_0` |
| `I_n` | `= frac{2n}{2n + 1} xx frac{2(n-1)}{2n-1} xx frac{2(n-2)}{2n-3} xx … xx frac{2}{3} xx 1` |
| `= frac{2n}{2n+1} xx frac{2n}{2n} xx frac{2(n-1)}{2n-1} xx frac{2(n-1)}{2n-2} xx … xx frac{2}{3} xx frac{2}{2} xx 1` | |
| `= frac{2^n (n xx (n-1) xx .. xx 1) xx 2^n (n xx (n – 1) xx … xx 1)}{(2n + 1)!}` | |
| `= frac{2^(2n) (n!)^2}{(2n + 1)!}` |
iii. `J_n = int_0^1 x^n (1-x)^n\ dx , \ n = 0, 1, 2, …`
| `text{Let} \ \ x` | `= sin^2 theta` |
| `frac{dx}{d theta}` | `= 2 sin theta \ cos theta \ => \ dx = 2 sin theta \ cos theta \ d theta` |
| `text{When}` | `x = 0 \ ,` | ` \ theta = 0` |
| `x = 1 \ ,` | ` \ theta = frac{pi}{2}` |
| `J_n` | `= int_0^(frac{pi}{2}) (sin^2 theta)^n (1 – sin^2 theta)^n * 2 sin theta \ cos theta \ d theta` |
| `= int_0^(frac{pi}{2}) sin^(2n) theta \ cos^(2n) theta * sin (2 theta)\ d theta` | |
| `= frac{1}{2^(2n)} int_0^(frac{pi}{2}) 2^(2n) sin^(2n) theta \ cos^(2n) theta * sin (2 theta)\ d theta` | |
| `= frac{1}{2^(2n)} int_0^(frac{pi}{2}) sin^(2n) (2 theta) * sin (2 theta)\ d theta` | |
| `= frac{1}{2^(2n)} int_0^(frac{pi}{2}) sin^(2n+1) (2 theta)\ d theta` | |
| `= frac{1}{2^(2n)} * frac{2^(2n) (n!)^2}{(2n+1)!}\ \ \ text{(using part (ii))}` | |
| `= frac{(n!)^2}{(2n + 1)!}` |
iv. `text{If} \ \ I_n ≤ 1,`
| `2^(2n) (n!)^2` | ` ≤ (2n + 1)!` |
| `(2^n n!)^2` | `≤ (2n + 1)!` |
`text{Show} \ \ I_n ≤ 1 :`
`text{Consider the graphs}`
`y = sin(2 theta) \ \ text{and}\ \ y = sin^(2n + 1) (2 theta) \ \ text{for} \ \ 0 ≤ theta ≤ frac{pi}{2}`
| `int_0^(frac{pi}{2}) sin(2 theta)` | `= [ – frac{1}{2} cos (2 theta) ]_0^(frac{pi}{2})` |
| `= – frac{1}{2} cos \ pi + frac{1}{2} cos \ 0` | |
| `= 1` |
`y = sin(2 theta) \ => \ text{Range} \ [0, 1] \ \ text{for}\ \ theta ∈ [0, frac{pi}{2}]`
| `sin^(2n+1) (2 theta)` | `≤ sin (2 theta) \ \ text{for}\ \ theta ∈ [0, frac{pi}{2}]` |
| `sin^(2n+1) (2 theta)` | `≤ 1` |
| `I_n` | `≤ 1` |
| `therefore (2^n n!)^2` | `≤ (2n + 1) !` |
Two similar right-angled triangles are shown.
The length of side `AB` is 8 cm and the length of side `EF` is 4 cm.
The area of triangle `ABC` is 20 cm2.
Calculate the length in centimetres of side `DF` in Triangle II, correct to two decimal places. (4 marks)
--- 8 WORK AREA LINES (style=lined) ---
`7.55\ \text{cm}`
`text{Consider} \ Δ ABC :`
| `text{Area}` | `= frac{1}{2} xx AB xx BC` |
| `20` | `= frac{1}{2} xx 8 xx BC` |
| `therefore \ BC` | `= 5` |
`text{Using Pythagoras in} \ Δ ABC :`
`AC = sqrt(8^2 + 5^2) = sqrt89`
`text{S} text{ince} \ Δ ABC\ text{|||}\ Δ DEF,`
| `frac{AC}{BC}` | `= frac{DF}{EF}` |
| `frac{sqrt89}{5}` | `= frac{DF}{4}` |
| `therefore \ DF` | `= frac{4 sqrt89}{5}` |
| `= 7.547 …` | |
| `= 7.55 \ text{cm (to 2 d.p.)}` |
--- 7 WORK AREA LINES (style=lined) ---
Show that `sin (3theta) = 1/2`. (2 marks)
--- 7 WORK AREA LINES (style=lined) ---
--- 10 WORK AREA LINES (style=lined) ---
i. `text(Prove:)\ \ sin^3 theta-3/4 sin theta + (sin(3theta))/4 = 0`
| `text(LHS)` | `= sin^3 theta-3/4 sin theta + 1/4 (sin 2thetacostheta + cos2thetasintheta)` |
| `= sin^3 theta-3/4 sintheta + 1/4(2sinthetacos^2theta + sintheta(1 – 2sin^2theta))` | |
| `= sin^3theta-3/4 sintheta + 1/4(2sintheta(1-sin^2theta) + sintheta – 2sin^3theta)` | |
| `= sin^3theta-3/4 sintheta + 1/4(2sintheta-2sin^3theta + sintheta-2sin^3theta)` | |
| `= sin^3theta-3/4sintheta + 3/4sintheta-sin^3theta` | |
| `= 0` |
ii. `text(Show)\ \ sin(3theta) = 1/2`
`text{Using part (i):}`
| `(sin(3theta))/4` | `= 3/4 sintheta-sin^3 theta` |
| `sin(3theta)` | `= 3sintheta-4sin^3theta\ …\ (1)` |
`x^3-12x + 8 = 0`
`text(Let)\ \ x = 4 sin theta`
| `(4sintheta)^3-12(4sintheta) + 8` | `= 0` |
| `64sin^3theta-48sintheta` | `= 0` |
| `−16underbrace{(3sintheta-4sin^2theta)}_text{see (1) above}` | `= −8` |
| `−16 sin(3theta)` | `= −8` |
| `sin(3theta)` | `= 1/2` |
iii. `text(Prove:)\ \ sin^2\ pi/18 + sin^2\ (5pi)/18 + sin^2\ (25pi)/18 = 3/2`
`text(Solutions to)\ \ x^3-12x + 8 = 0\ \ text(are)`
`x = 4sintheta\ \ text(where)\ \ sin(3theta) = 1/2`
`text(When)\ \ sin3theta = 1/2,`
| `3theta` | `= pi/6, (5pi)/6, (13pi)/6, (17pi)/6, (25pi)/6, (29pi)/6, …` |
| `theta` | `= pi/18, (5pi)/18, (13pi)/18, (17pi)/18, (25pi)/18, (29pi)/18, …` |
`:.\ text(Solutions)`
`x = 4sin\ pi/18 \ \ \ (= 4sin\ (17pi)/18)`
`x = 4sin\ (5pi)/18 \ \ \ (= 4sin\ (13pi)/18)`
`x = 4sin\ (25pi)/18 \ \ \ (= 4sin\ (29pi)/18)`
`text(If roots of)\ \ x^3-12x + 8 = 0\ \ text(are)\ \ α, β, γ:`
`α + β + γ = −b/a = 0`
`αβ + βγ + αγ = c/a = −12`
| `(4sin\ pi/18)^2 + (4sin\ (5pi)/18)^2 + (4sin\ (25pi)/18)^2` | `= (α + β + γ)^2 – 2(αβ + βγ + αγ)` |
| `16(sin^2\ pi/18 + sin^2\ (5pi)/18 + sin^2\ (25pi)/18)` | `= 0-2(−12)` |
| `:. sin^2\ pi/18 + sin^2\ (5pi)/18 + sin^2\ (25pi)/18` | `= 24/16=3/2` |
There are two tanks on a property, Tank A and Tank B. Initially, Tank A holds 1000 litres of water and Tank B is empty.
The volume of water in Tank A is modelled by `V = 1000 - 20t` where `V` is the volume in litres and `t` is the time in minutes from when the tank begins to lose water.
On the grid below, draw the graph of this model and label it as Tank A. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
a. `text{T} text{ank} \ A \ text{will pass trough (0, 1000) and (50, 0)}`
b. `text{T} text{ank} \ B \ text{will pass through (15, 0) and (45, 900)}`
`text{By inspection, the two graphs intersect at} \ \ t = 29 \ text{minutes}`
c. `text{Strategy 1}`
`text{By inspection of the graph, consider} \ \ t = 45`
`text{T} text{ank A} = 100 \ text{L} , \ text{T} text{ank B} =900 \ text{L} `
`:.\ text(Total volume = 1000 L when t = 45)`
`text{Strategy 2}`
| `text{Total Volume}` | `=text{T} text{ank A} + text{T} text{ank B}` |
| `1000` | `= 1000 – 20t + (t – 15) xx 30` |
| `1000` | `= 1000 – 20t + 30t – 450 ` |
| `10t` | `= 450` |
| `t` | `= 45 \ text{minutes}` |
A plumber charges a call-out fee of $90 as well as $2 per minute while working.
Suppose the plumber works for `t` hours.
Which equation expresses the amount the plumber charges ($`C`) as a function of time (`t` hours)?
`D`
| `text(Hourly rate)` | `= 60 xx 2` |
| `= $120` |
`therefore C = 90 + 120t`
What is 0.002073 expressed in standard form with two significant figures?
`B`
| `0.002073` | `= 2.073 xx 10^(-3)` | |
| `=2.1 xx 10^(-3)\ \ \ text{(to 2 sig fig)}` |
`=> B`
Wilma deposited a lump sum into a new bank account which earns 2% per annum compound interest.
Present value interest factors for an annuity of $1 for various interest rates (`r`) and numbers of periods (`N`) are given in the table.
Wilma was able to make the following withdrawals from this account.
Calculate the minimum lump sum Wilma must have deposited when she opened the new account. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
`$ 34 \ 486`
`text{Annuity 1:}\ PV\ text{of $1000 annuity for 20 years at} \ \ r = 0.02`
`PV\ text{factor} = 16.351`
| `therefore \ PV\ text{Annuity 1}` | `= 16.351 xx 1000` |
| `= $16 \ 351` |
`text{Annuity 2:}\ PV\ text{of $3000 annuity for years 21-30 at} \ \ r = 0.02`
| `PV\ text{Annuity 2}` | `= PVtext{(30 years)} – PVtext{(20 years)}` |
| `= 3000 xx 22.396 – 3000 xx 16.351` | |
| `= $ 18 \ 135` |
| `:.\ text{Lump sum required}` | `= 16 \ 351 + 18\ 135` |
| `= $ 34 \ 486` |
Suppose `f(x) = tan(cos^(-1)(x))` and `g(x) = (sqrt(1-x^2))/x`.
The graph of `y = g(x)` is given.
--- 8 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
i. `f(x) = tan(cos^(-1)(x))`
| `f^(′)(x)` | `= -1/sqrt(1-x^2) · sec^2(cos^(-1)(x))` |
| `= -1/sqrt(1-x^2) · 1/(cos^2(cos^(-1)(x)))` | |
| `= -1/(x^2sqrt(1-x^2))` |
`g(x) = (1-x^2)^(1/2) · x^(-1)`
| `g^(′)(x)` | `= 1/2 · -2x(1-x^2)^(-1/2) · x^(-1)-(1-x^2)^(1/2) · x^(-2)` |
| `= (-x)/(x sqrt(1-x^2))-sqrt(1-x^2)/(x^2)` | |
| `= (-x^2-sqrt(1-x^2) sqrt(1-x^2))/(x^2 sqrt(1-x^2))` | |
| `= (-x^2-(1-x^2))/(x^2sqrt(1-x^2))` | |
| `= -1/(x^2sqrt(1-x^2))` | |
| `=f^(′)(x)` |
ii. `f^(′)(x) = g^(′)(x)`
`=> f(x) = g(x) + c`
`text(Find)\ c:`
| `f(1)` | `= tan(cos^(-1) 1)` |
| `= tan 0` | |
| `= 0` |
`g(1) = sqrt(1-1)/0 = 0`
`f(1) = g(1) + c`
`:. c = 0`
`:. f(x) = g(x)`
The intelligence Quotient (IQ) scores for adults in City A are normally distributed with a mean of 108 and a standard deviation of 10.
The IQ score for adults in City B are normally distributed with a mean of 112 and a standard deviation of 16.
--- 4 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
a. `text{In City A:}`
`z text{-score}\ (128) = frac {x -mu}{sigma} = frac{128 – 108}{10} = 2`
`therefore\ text{2.5% have a higher IQ in City} \ A.`
b. `text{In City B:}`
`z text{-score}\ (128) = frac{128 – 112}{16} = 1`
`therefore \ text{Adults in City} \ B \ text{with an IQ}\ < 128`
`= 84text(%) xx 1 \ 000 \ 000`
`= 840 \ 000`
c. `z text{-score in City A}\ = z text{-score in City B}`
| `frac{x – 108}{10} ` | `= frac{x -112}{16} \ \ text{(multiply b.s.} \ xx 160 text{)}` |
| `16 (x – 108)` | `= 10 (x – 112)` |
| `16 x – 1728` | `= 10 x – 1120` |
| `6x` | `= 608` |
| `x` | `= 101.3` |
`therefore \ text{Simon’s IQ} = 101.3 \ text{(to 1 d.p.)}`
A cricket is an insect. The male cricket produces a chirping sound.
A scientist wants to explore the relationship between the temperature in degrees Celsius and the number of cricket chirps heard in a 15-second time interval.
Once a day for 20 days, the scientist collects data. Based on the 20 data points, the scientist provides the information below.
The scientist fits a least-squares regression line using the data `(x, y)`, where `x` is the temperature in degrees Celsius and `y` is the number of chirps heard in a 15-second time interval. The equation of this line is
`y = −10.6063 + bx`,
where `b` is the slope of the regression line.
The least-squares regression line passes through the point `(barx, bary)`, where `barx` is the sample mean of the temperature data and `bary` is the sample mean of the chirp data.
Calculate the number of chirps expected in a 15-second interval when the temperature is 19° Celsius. Give your answer correct to the nearest whole number. (5 marks)
`29\ text(chirps)`
`y = −10.6063 + bx`
`text(Find)\ b:`
`text(Line passes through)\ \ (barx, bary)`
| `barx` | `= 22 – 0.525` |
| `= 21.475` |
| `bary` | `= text(total chirps)/text(number of data points)` |
| `= 684/20` | |
| `= 34.2` |
| `34.2` | `= −10.6063 + b(21.475)` |
| `:.b` | `= 44.8063/21.475` |
| `~~ 2.0864` |
`text(If)\ \ x = 19,`
| `y` | `= −10.6063 + 2.0864 xx 19` |
| `= 29.03` | |
| `= 29\ text(chirps)` |
The graph shows the number of bacteria, `y`, at time `n` minutes. Initially (when `n = 0`) the number of bacteria is 1000.
--- 1 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
a. `text{When} \ \ n = 40,`
`text{Number of Bacteria} \ (y) = 4000`
b. `A = 1000 \ => \ y = 1000 b^n`
`text{By inspection, graph passes through (40, 4000)}`
`=> \ 4000 = 1000 b^40`
`text(Guess and check possible values of)\ b:`
`text{If} \ \ b = 1.03 \ , \ \ y = 1000 xx 1.03^40 = 3262 \ text{(too low)}`
`text{If} \ \ b = 1.04 \ , \ \ y = 1000 xx 1.04^40 = 4801 \ text{(too high)}`
`therefore \ 1.03 < b < 1.04`
to show that
`((2n),(n)) = ((n),(0))^2 + ((n),(1))^2 + … + ((n),(n))^2`,
where `n` is a positive integer. (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
A group consisting of an even number `(0, 2, 4, …, 2n)` of members is chosen, with the number of men equal to the number of women.
Show, giving reasons, that the number of ways to do this is `((2n),(n))`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Show, giving reasons, that the number of ways to choose the even number of people and then the leaders is
`1^2 ((n),(1))^2 + 2^2((n),(2))^2 + … + n^2((n),(n))^2`. (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
By considering this reversed process and using part (ii), find a simple expression for the sum in part (iii). (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
i. `text(Expand)\ \ (1 + x)^(2n):`
`\ ^(2n)C_0 + \ ^(2n)C_1 x^2 + … + \ ^(2n)C_n x^n + … \ ^(2n)C_(2n) x^(2n)`
`=> text(Coefficient of)\ \ x^n = \ ^(2n)C_n`
`text(Expand)\ \ (1 + x)^n (1 + x)^n:`
`[\ ^nC_0 + \ ^nC_1 x + … + \ ^nC_n x^n][\ ^nC_0 + \ ^nC_1 x + … + \ ^nC_n x^n]`
`=> \ text(Coefficient of)\ \ x^n`
`= \ ^nC_0 · \ ^nC_n + \ ^nC_1 · \ ^nC_(n – 1) + … + \ ^nC_(n – 1) · \ ^nC_1 + \ ^nC_n · \ ^nC_0`
`= (\ ^nC_0)^2 + (\ ^nC_1)^2 + … + (\ ^nC_(n – 1))^2 + (\ ^nC_n)^2\ \ \ (\ ^nC_k = \ ^nC_(n – k))`
`text(Equating coefficients:)`
`\ ^(2n)C_n = (\ ^nC_0)^2 + (\ ^nC_1)^2 + … + (\ ^nC_n)^2`
ii. `text(Number of men = Number of women)\ \ (M = W)`
| `text(If)\ \ M = W = 0:` | `text(Ways) = \ ^nC_0 · \ ^nC_0 = (\ ^nC_0)^2` |
| `text(If)\ \ M = W = 1:` | `text(Ways) = \ ^nC_1 · \ ^nC_1 = (\ ^nC_1)^2` |
`vdots`
`text(If)\ \ M = W = n: text(Ways) = \ ^nC_n · \ ^nC_n = (\ ^nC_n)^2`
`:.\ text(Total combinations)`
`= (\ ^nC_0)^2 + (\ ^nC_1)^2 + … + (\ ^nC_n)^2`
`= \ ^(2n)C_n\ \ \ text{(from part (i))}`
iii. `text(Let)\ \ M_L = text(possible male leaders)`
`text(Let)\ \ W_L = text(possible female leaders)`
`text(If)\ \ M = W = 0 => text(no leaders)`
`text(If)\ \ M = W = 1: text(Ways) = \ ^nC_1 xx M_L xx \ ^nC_1 xx W_L = 1^2 (\ ^nC_1)^2`
`text(If)\ \ M = W = 2: text(Ways) = \ ^nC_2 xx 2 xx \ ^nC_2 xx 2 = 2^2 (\ ^nC_2)^2`
`vdots`
`text(If)\ \ M = W = n: text(Ways) = \ ^nC_n xx n xx \ ^nC_2 xx n = n^2 (\ ^nC_n)^2`
`:.\ text(Total combinations)`
`= 1^2(\ ^nC_1)^2 + 2^2(\ ^nC_2)^2 + … + n^2(\ ^nC_n)^2`
| iv. | `text(If)\ \ M = W = 1: text(Ways)` | `= M_L xx \ ^(n – 1)C_0 xx W_L xx \ ^(n – 1)C_0` |
| `= n xx \ ^(n – 1)C_0 xx n xx \ ^(n – 1)C_0` | ||
| `= n^2(\ ^(n – 1)C_0)^2` |
| `text(If)\ \ M = W = 2: text(Ways)` | `= n xx \ ^(n – 1)C_1 xx n xx \ ^(n – 1)C_1` |
| `= n^2(\ ^(n – 1)C_1)^2` |
`vdots`
| `text(If)\ \ M = W = n:\ text(Ways)` | `= n xx \ ^(n – 1)C_(n – 1) xx n xx \ ^(n – 1)C_(n – 1)` |
| `= n^2(\ ^(n – 1)C_(n – 1))^2` |
`:.\ text(Total combinations)`
`= n^2(\ ^(n – 1)C_0)^2 + n^2(\ ^(n – 1)C_1)^2 + … + n^2(\ ^(n – 1)C_(n – 1))^2`
`= n^2 xx \ ^(2(n – 1))C_(n – 1)\ \ \ text{(using part (i))}`
`= n^2 xx \ ^(2n – 2)C_(n – 1)`
The population of mice on an isolated island can be modelled by the function.
`m(t) = a sin (pi/26 t) + b`,
where `t` is the time in weeks and `0 <= t <= 52`. The population of mice reaches a maximum of 35 000 when `t=13` and a minimum of 5000 when `t = 39`. The graph of `m(t)` is shown.
--- 3 WORK AREA LINES (style=lined) ---
Find the values of `t, \ 0 <= t <= 52`, for which both populations are increasing. (3 marks)
--- 7 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
| a. | `b` | `= (35\ 000 + 5000)/2` |
| `= 20\ 000` |
| `a` | `=\ text(amplitude of sin graph)` |
| `= 35\ 000 – 20\ 000` | |
| `= 15\ 000` |
b. `text(By inspection of the)\ \ m(t)\ \ text(graph)`
`m^{′}(t) > 0\ \ text(when)\ \ 0 <= t < 13\ \ text(and)\ \ 39 < t <= 52`
`text(Sketch)\ \ c(t):`
`text(Minimum)\ \ (cos0)\ \ text(when)\ \ t = 10`
`text(Maximum)\ \ (cospi)\ \ text(when)\ \ t = 36`
`:. c^{′}(t) > 0\ \ text(when)\ \ 10 < t < 36`
`:. text(Both populations are increasing when)\ \ 10 < t < 13`
c. `c(t)\ text(maximum when)\ \ t = 36`
| `m(t)` | `= 15\ 000 sin(pi/26 t) + 20\ 000` |
| `m^{′}(t)` | `= (15\ 000pi)/26 cos(pi/26 t)` |
| `m^{′}(36)` | `= (15\ 000pi)/26 · cos((36pi)/26)` |
| `= -642.7` |
`:.\ text(Mice population is decreasing at 643 mice per week.)`
The graph shows two functions `y = f(x)` and `y = g(x)`.
Define `h(x) = f(g(x))`.
How many stationary points does `y = h(x)` have for `1 <= x <= 5`?
`D`
`h(x) = f(g(x))`
`h′(x) = g′(x) xx f′(g(x))`
`text(S.P.’s occur when)\ \ g′(x) = 0\ \ text(or)\ \ f′(g(x)) = 0`
`g′(x) = 0\ \ text(when)\ \ x =3\ (text(from graph))`
`f′(x) = 0\ \ text(when)\ \ x ~~ 1 \ \ text{(i.e.}\ xtext{-value is just under 1)}`
`text(Find values of)\ x\ text(when)\ g(x) ~~ 1:`
`text(By inspection, there are 2 values where)`
`g(x) ~~ 1, \ x ∈ [1, 5]`
`:.\ text(There are 3 S.P.’s for)\ y = h(x), \ x ∈ [1, 5]`
`=> D`
When Jake stops drinking alcohol at 10:30 pm, he has a blood alcohol content (BAC) of 0.08375.
The number of hours required for a person to reach zero BAC after they stop consuming alcohol is given by the formula
`text(Time) = frac{ text(BAC)}{0.015}`.
At what time on the next day should Jake expect his BAC to be 0.05?
`A`
`text(Time from 0.08375 → 0 BAC)`
`= frac(0.08375)(0.015)`
`approx 5.58 \ text(hours)`
`text(Time from 0.08375 → 0.05 BAC)`
`approx frac{(0.08375 – 0.05)}{0.08375} xx 5.58`
`approx 0.4 xx 5.58`
`approx 2.25\ text(hours)`
| `therefore \ text(Time)` | `approx \ 10:30 \ text(pm) \ + 2 \ text(hr) \ 15 \ text(min)` |
| `approx \ 12:45 \ text(am)` |
`=> \ A`
A particle with mass `m` moves horizontally against a resistance force `F`, equal to `mv(1 + v^2)` where `v` is the particle's velocity.
Initially, the particle is travelling in a positive direction from the origin at velocity `T`.
--- 6 WORK AREA LINES (style=lined) ---
--- 8 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
i. `text(Newton’s 2nd law:)`
`F = mddotx = −mv(1 + v^2)`
| `v · (dv)/(dx)` | `= −v(1 + v^2)` |
| `(dv)/(dx)` | `= −(1 + v^2)` |
| `(dx)/(dv)` | `= −1/(1 + v^2)` |
| `x` | `= −int 1/(1 + v^2)\ dv` |
| `= −tan^(−1) v + C` |
`text(When)\ \ x = 0, v = T:`
`C = tan^(−1)T`
`x = tan^(−1)T – tan^(−1)v`
`text(Let)\ \ x = A – B`
`A = tan^(−1) T \ => \ T = tan A`
`B = tan^(−1)v \ => \ v = tan B`
| `tan x` | `= tan(A – B)` |
| `= (tan A – tan B)/(1 + tan A tan B)` | |
| `= (T – v)/(1 + Tv)` | |
| `:. x` | `= tan^(−1)((T – v)/(1 + Tv))` |
ii. `text(Using)\ \ ddotx = (dv)/(dt):`
`(dv)/(dt) = −1/(v(1 + v^2))`
`t = −int 1/(v(1 + v^2)) dv`
`text(Using Partial Fractions):`
`1/(v(1 + v^2)) = A/v + (Bv + C)/(1 + v^2)`
`A(1 + v^2) + (Bv + C)v = 1`
`A = 1`
| `(A + B)v^2` | `= 0` | `=> ` | `B` | `= −1` |
| `Cv` | `= 0` | `=> ` | `C` | `= 0` |
| `t` | `= −int 1/v\ dv + int v/(1 + v^2)\ dv` |
| `= −log_e v + 1/2 int(2v)/(1 + v^2)\ dv` | |
| `= −log_e v + 1/2 log_e (1 + v^2) + C` | |
| `= −1/2 log_e v^2 + 1/2 log_e (1 + v^2) + C` | |
| `= 1/2 log_e ((1 + v^2)/(v^2)) + C` |
`text(When)\ \ t = 0, v = T:`
`C = −1/2 log_e ((1 + T^2)/(T^2))`
| `:. t` | `= 1/2 log_e ((1 + v^2)/(v^2)) – 1/2 log_e((1 + T^2)/(T^2))` |
| `= 1/2 log_e (((1 + v^2)/(v^2))/((1 + T^2)/(T^2)))` | |
| `= 1/2 log_e ((T^2(1 + v^2))/(v^2(1 + T^2)))` |
| iii. | `t` | `= 1/2 log_e ((T^2(1 + v^2))/(v^2(1 + T^2)))` |
| `e^(2t)` | `= (T^2(1 + v^2))/(v^2(1 + T^2))` | |
| `1 + v^2` | `= (e^(2t)v^2(1 + T^2))/(T^2)` | |
| `1` | `= v^2((e^(2t)(1 + T^2))/(T^2) – 1)` | |
| `1` | `= v^2((e^(2t)(1 + T^2) – T^2)/(T^2))` | |
| `:. v^2` | `= (T^2)/(e^(2t)(1 + T^2) – T^2)` |
`text(As)\ \ t -> ∞:`
`v^2 -> 0, \ v -> 0`
`x = tan^(−1)T – tan^(−1)v`
`x -> tan^(−1)T`
A young tree is protected by a tree guard in the shape of a square-based pyramid.
The height of the tree guard is 54 cm, as shown in the diagram below.
The top section of the tree guard is removed along the dotted line to allow the tree to grow.
Removing this top section decreases the height of the tree guard to 45 cm, as shown in the diagram below.
The ratio of the volume of the tree guard that is removed to the volume of the tree guard that remains is
`D`
`text(Top section is similar to full tree guard.)`
| `text(Ratio of sides)` | `= (54 – 45) : 54` |
| `= 9:54` | |
| `= 1:6` |
| `:. \ text(V)_1 : text(V)_2` | `= 1^3 : 6^3` |
| `= 1 : 216` |
`text(However V)_2 \ text(is the volume of a full tree guard. )`
`text(We need volume of the remaining tree guard.)`
`:. \ V_1 : V_2 \ text{(remains)} = 1:215`
`=> \ D`
Let diagram below shows a trapezium with vertices at `(0, 0), (0, 2), (3, 2)` and `(b, 0)`, where `b` is a real number and `0 < b < 2`
On the same axes as the trapezium, part of the graph of a cubic polynomial function is drawn. It has the rule `y = ax(x-b)^2`, where `a` is a non-zero real number and `0 ≤ x ≤ b`.
--- 5 WORK AREA LINES (style=lined) ---
The area between the graph of the function and the `x`-axis is removed from the trapezium, as shown in the diagram.
--- 8 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
| a. `y` | `= ax(x-b)^2` |
| `y^{′}` | `= a(x-b)^2 + 2ax(x-b)` |
| `= a(x-b)(x-b + 2x)` | |
| `= a(x-b)(3x-b)` |
`text(S) text(olve) \ \ y^{′} = 0 \ \ text(for) \ x:`
`x = b \ \ text(or) \ \ (b)/(3)`
`y_text(max) = b \ \ text{(given) and occurs at} \ \ x = (b)/(3)`
| `b` | `= a((b)/(3))((b)/(3)-b)^2` |
| `b` | `= a((b)/(3))((4b^2)/(9))` |
| `b` | `= a((4b^3)/(27))` |
`:. \ a = (27)/(4b^2)`
b. `text(Let)\ \ A_1 = \ text(area under the graph)`
| `A_1` | `= int_0^b ax (x-b)^2 dx` |
| `= a int_0^b x(x^2-2bx + b^2)\ dx` | |
| `= (27)/(4b^2) int_0^b x^3-2bx^2 + b^2 x \ dx` | |
| `= (27)/(4b^2) [(x^4)/(4)-(2bx^3)/(3) + (b^2 x^2)/(2)]_0^b` | |
| `= (27)/(4b^2) ((b^4)/(4)-(2b^4)/(3) + (b^4)/(2))` | |
| `= (27)/(4b^2) ((b^4)/(12))` | |
| `= (9b^2)/(16)` |
`text(Let) \ \ A_2 = \ text(area of triangle)`
`A_2 = (1)/(2) xx 2 xx (3-b) = 3-b`
| `:. \ text(Shaded region)` | `= 6-(9b^2)/(16)-(3-b)` |
| `= b + 3-(9b^2)/(16)` |
c. `A = b + 3-(9b^2)/(16)`
`(dA)/(db) = 1-(9b)/(8)`
`(dA^2)/(db^2) =-(9)/(8) <0`
`=>\ text{SP (max) when} \ \ (dA)/(db) = 0`
`(9b)/(8) = 1 \ => \ \ b = (8)/(9)`
| `:. A_(max)` | `= (8)/(9) + 3-{9((8)/(9))^2}/{16}` |
| `= (35)/(9)-(64)/(9 xx 16)` | |
| `= (31)/(9)` |
Robyn has a current balance of $347 283.45 in her superannuation account.
Robyn’s employer deposits $350 into this account every fortnight.
This account earns interest at the rate of 2.5% per annum, compounding fortnightly.
Robyn will stop work after 15 years and will no longer receive deposits from her employer.
The balance of her superannuation account at this time will be invested in an annuity that will pay interest at the rate of 3.6% per annum, compounding monthly.
After 234 monthly payments there will be no money left in Robyn’s annuity.
The value of Robyn’s monthly payment will be closest to
`A`
`text(Balance after 15 years (by TVM Solver):)`
| `N` | `= 26 xx 15 = 390` |
| `Itext(%)` | `= 2.5` |
| `PV` | `= 347\ 283.45` |
| `PMT` | `= 350` |
| `FV` | `= ?` |
| `text(P/Y)` | `= 26` |
| `text(C/Y)` | `= 26` |
`=>\ 670\ 724.87`
`text(Monthly payment (by TVM Solver)):`
| `N` | `= 234` |
| `Itext(%)` | `= 3.6` |
| `PV` | `= 670\ 724.87` |
| `PMT` | `= ?` |
| `FV` | `= 0` |
| `text(P/Y)` | `= 12` |
| `text(C/Y)` | `= 12` |
`=> PMT = −3993.31`
`=>\ A`
A record producer gave the band $50 000 to write and record an album of songs.
This $50 000 was invested in an annuity that provides a monthly payment to the band.
The annuity pays interest at the rate of 3.12% per annum, compounding monthly.
After six months of writing and recording, the band has $32 667.68 remaining in the annuity.
--- 2 WORK AREA LINES (style=lined) ---
To extend the time that the annuity will last, the band will work for three more months without withdrawing a payment.
After this, the band will receive monthly payments of $3800 for as long as possible.
The annuity will end with one final monthly payment that will be smaller than all of the others.
Calculate the total number of months that this annuity will last. (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
a. `text(By TVM Solver:)`
| `N` | `= 6` | |
| `I text(%)` | `=3.12` | |
| `PV` | `=50\ 000` | |
| `PMT` | `= ?` | |
| `FV` | `=-32\ 667.68` | |
| `text(PY)` | `= text(CY) = 12` |
`=> PMT = -3000.00`
`:. \ text(Monthly payment) = $3000`
b. `text{Value after 3 more months (by TVM Solver):}`
| `N` | `= 3` | |
| `I text(%)` | `=3.12` | |
| `PV` | `=32\ 667.68` | |
| `PMT` | `= 0` | |
| `FV` | `=?` | |
| `text(PY)` | `= text(CY) = 12` |
`=> FV = -32\ 923.15`
`text(Find) \ \ N \ text(when) \ FV= 0 \ text{(by TVM Solver):}`
| `N` | `= ?` | |
| `I text(%)` | `=3.12` | |
| `PV` | `=-32\ 923.15` | |
| `PMT` | `= 3800` | |
| `FV` | `=0` | |
| `text(PY)` | `= text(CY) = 12` |
`=> N = 8.77`
| `:. \ text(Total months of annuity)` | `= 6 + 3 + 9` |
| `= 18` |
A random sample of 12 mammals drawn from a population of 62 types of mammals was categorized according to two variables. likelihood of attack (1 = low, 2 = medium, 3 = high) exposure to attack during sleep (1 = low, 2 = medium, 3 = high) The data is shown in the following table. --- 0 WORK AREA LINES (style=lined) --- The following two-way frequency table was formed from the data generated when the entire population of 62 types of mammals was similarly categorized. --- 5 WORK AREA LINES (style=lined) --- --- 2 WORK AREA LINES (style=lined) --- --- 4 WORK AREA LINES (style=lined) ---
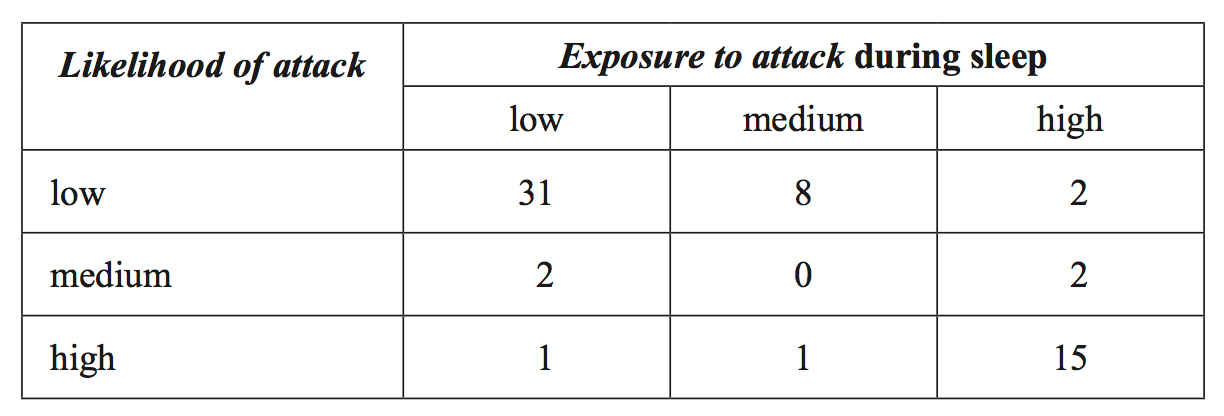
`= 50 %`
`text(of attack is associated with low exposure to attack during sleep.)`
`text(- 91%) \ ({31}/{34}) \ text(of animals with low exposure to attack)`
`text(during sleep, have a low likelihood of attack.)`
`text(- Similarly, 89% of animals with a medium exposure to attack during)`
`text(sleep have a low likelihood of attack.)`
`text(- 11% of animals with a high exposure to attack during sleep have)`
`text(a low likelihood of attack)`
a. b. i. `15` iii. `text(The data supports the contention that animals with a low likelihood)` `text(of attack is associated with low exposure to attack during sleep.)` `text(- 91%) \ ({31}/{34}) \ text(of animals with low exposure to attack)` `text(during sleep, have a low likelihood of attack.)` `text(- Similarly, 89% of animals with a medium exposure to attack during)` `text(sleep have a low likelihood of attack.)` `text(- 11% of animals with a high exposure to attack during sleep have)` `text(a low likelihood of attack)`
ii. `text(Percentage)`
`= (2)/(4) xx 100`
`= 50%`
A farm contains four water sources, `P`, `Q`, `R` and `S`.
Part 1
Cows on the farm are free to move between the four water sources.
The change in the number of cows at each of these water sources from week to week is shown in the transition diagram below.
Let `C_n` be the state matrix for the location of the cows in week `n` of 2019.
The state matrix for the location of the cows in week 23 of 2019 is `C_23 = [(180),(200),(240),(180)]{:(P),(Q),(R),(S):}`
The state matrix for the location of the cows in week 24 of 2019 is `C_24 = [(160),(222),(203),(215)]{:(P),(Q),(R),(S):}`
Of the cows expected to be at `Q` in week 24 of 2019, the percentage of these cows at `R` in week 23 of 2019 is closest to
Part 2
Sheep on the farm are also free to move between the four water sources.
The change in the number of sheep at each water source from week to week is shown in matrix `T` below.
`{:(),(),(T=):}{:(qquadqquadqquadtext(this week)),((qquadP,quadQ,quadR,quadS)),([(0.4,0.3,0.2,0.1),(0.2,0.1,0.5,0.3),(0.1,0.3,0.1,0.2),(0.3,0.3,0.2,0.4)]):}{:(),(),({:(P),(Q),(R),(S):}):}{:(),(),(text(next week)):}`
In the long term, 635 sheep are expected to be at `S` each week.
In the long term, the number of sheep expected to be at `Q` each week is closest to
`text(Part 1:)\ D`
`text(Part 2:)\ C`
`text(Part 1)`
`text(In week 23, 240 cows are at)\ R.`
`text(In week 24, number of cows moving from)\ R\ text(to)\ Q`
`=20text(%) xx 240`
`= 48\ text(cows)`
`text(Total cows at)\ Q = 222`
| `:.\ text(Percentage)` | `= 48/222` |
| `= 0.2162` | |
| `= 22text(%)` |
`=>\ D`
`text(Part 2)`
`T^50 = [(0.2434, 0.2434, 0.2434, 0.2434),(0.2603, 0.2603, 0.2603, 0.2603),(0.1834, 0.1834, 0.1834, 0.1834),(0.3130, 0.3130, 0.3130, 0.3130)]`
`text(S)text(ince 635 sheep are expected long term at)\ S,`
| `text(Total sheep)` | `= 635/0.3130` |
| `= 2029` |
`:. text(Long term expected at)\ Q`
`~~ 0.2603 xx 2029`
`~~ 528`
`=>\ C`
Jamie sold bottles of homemade lemonade to his neighbours on Saturday.
The revenue, in dollars, he made from selling `n` bottles of lemonade is given by
revenue = 3.5`n`
The cost, in dollars, of making `n` bottles of lemonade is given by
cost = 60 + `n`
The profit made by Jamie on Saturday could have been
`B`
| `text(Profit)` | `= R – C` |
| `= 3.5n – (60 + n)` | |
| `= 2.5n – 60` |
`text(If profit is a whole number)`
`=> n\ text(must be even)`
`=>\ text(revenue total must be a multiple of $5)`
`=>\ text(profit total must be a multiple of $5)`
`=> B`
A landscape gardener is planning the construction of a garden.
This project requires 13 activities, `I` to `U`.
The directed graph below shows each of these activities represented by edges.
The numbers on the edges are the durations of the activities, in days.
The cost of reducing the completion time of any activity in this project is $1000 per day.
The landscape gardener has a maximum of $3000 to spend on reducing the minimum completion time of this project.
The total completion time of the project can be reduced by three days by reducing
`B`
Let `f: R → R, \ f(x) = e^((x/2))` and `g: R → R, \ g(x) = 2log_e(x)`.
--- 4 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
Let `B` be the point of intersection of the graphs of `g` and `y =-x + 2log_e(2) + 2`, as shown in the diagram below.
--- 4 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
Let `p : R→ R, \ p(x) = e^(kx)` and `q : R→ R, \ q(x) = (1)/(k) log_e(x)`.
--- 6 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
a. `g(x) = 2log_e x`
`text(Inverse: swap) \ x ↔ y`
| `x` | `= 2log_e y` |
| `log_e y` | `= (x)/(2)` |
| `y` | `= e^{(x)/(2)}` |
b. `f(x) = e^{(x)/(2)}`
`f′(x) = (1)/(2) e^{(x)/(2)}`
`text(S) text(olve) \ \ f′(x) = 1 \ text(for) \ x:`
`x = 2log_e 2`
`y = e^(log_e 2) = 2`
`:. \ A\ text(has coordinates)\ (2log_e 2, 2)`
c. `m_(⊥) = -1`
`text(Equation of line) \ \ m = -1 \ \ text(through)\ \ (2log_e 2, 2) :`
| `y-2` | `= -(x-2log_e 2)` |
| `y` | `= -x + 2log_e 2 + 2` |
d. `text(Method 1)`
`text(S) text(olve for) \ x :`
`-x + 2log_e 2 + 2 = 2log_e x`
`=> x = 2 , \ y = 2log_e 2`
`:. B ≡ (2, 2log_e 2)`
`text(Method 2)`
`text(S) text(ince) \ \ f(x) = g^-1 (x)`
`B \ text(is the reflection of) \ \ A(2log_e 2, 2) \ \ text(in the) \ \ y=x \ \ text(axis)`
`:. \ B ≡ (2, 2log_e 2)`
e.
`y = g(x) \ \ text(intersects) \ x text(-axis at) \ \ x = 1`
`text(Dividing shaded area into 3 sections:)`
| `A` | `= int_0^1 f(x)\ dx \ + \ int_1^(2log_e 2) f(x)-g(x)\ dx` | |
| ` \ + \ int_(2log_e 2)^2 (-x + 2log_e 2 + 2)-g(x)\ dx` | ||
| `= 6-2(log_e 2)^2-4 log_e 2` |
f. `p(x) = e^(kx) \ , \ q(x) = (1)/(k) log_e x`
`p′(x) = k e^(kx) \ , \ q′(x) = (1)/(kx)`
`text(S) text(ince graphs touch on) \ y = x`
`k e^(kx) = 1\ …\ (1)`
`(1)/(kx) = 1\ …\ (2)`
`text(Substitute) \ x = (1)/(k) \ text{from (2) into (1)}`
| `k e^(k xx 1/k)` | `= 1` |
| `:. k` | `= (1)/(e)` |
g. `text(Consider)\ \ p(x):`
`text(When) \ \ x = 0 , \ p(0) = 1 , \ p′(0) = k`
`text(Consider) \ \ q(x):`
`text(When) \ \ y= 0, \ (1)/(k) log_e x = 0 \ => \ x = 1`
`q′(1) = (1)/(k)`
`text(If lines are parallel), \ k = (1)/(k)`
`:. \ k = 1`
A mining company has found deposits of gold between two points, `A` and `B`, that are located on a straight fence line that separates Ms Pot's property and Mr Neg's property. The distance between `A` and `B` is 4 units.
The mining company believes that the gold could be found on both Ms Pot's property and Mr Neg's property.
The mining company initially models he boundary of its proposed mining area using the fence line and the graph of
`f : [0, 4] → R, \ f(x) = x(x-2)(x-4)`
where `x` is the number of units from point `A` in the direction of point `B` and `y` is the number of units perpendicular to the fence line, with the positive direction towards Ms Pot's property. The mining company will only mine from the boundary curve to the fence line, as indicated by the shaded area below.
--- 3 WORK AREA LINES (style=lined) ---
The mining company offers to pay Mr Neg $100 000 per square unit of his land mined and Ms Pot $120 000 per square unit of her land mined.
--- 2 WORK AREA LINES (style=lined) ---
The mining company reviews its model to use the fence line and the graph of
`p : [0, 4] → R, \ p(x) = x(x-4 + (4)/(1 + a)) (x-4)` where `a > 0`.
--- 3 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
Mr Neg does not want his property to be mined further than 4 units measured perpendicular from the fence line.
--- 5 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
| a. `A` | `= int_0^2 x(x-2)(x-4)\ dx – int_2^4 x(x-2)(x-4)\ dx` |
| `= 4-(-4)` | |
| `= 8` |
| b. `text(Total payment)` | `= 4 xx 100 000 + 4 xx 120 000` |
| `= $880\ 000` |
c. `text(If) \ \ p(x) = f(x)`
| `x-2` | `= x-4 + (4)/(1 + a)` | |
| `(4)/(1 + a)` | `=2` | |
| `:. a` | `=1` |
d. `p^{′}(x) = (3(a + 1) x^2-8(2a + 1) x + 16a)/(a + 1) \ \ \ text{(by CAS)}`
`text(S) text(olve) \ \ p^{′}(x) = 0 \ \ text(for) \ \ x :`
`x = ((8a + 4) ± 4 sqrt(a^2 + a + 1))/(3a +3) \ , \ a > 0`
e. `text(If no mining further than 4 units,) \ \ p(x) ≥-4`
`text(Max distance from Mr Neg’s fence occurs when) \ \ 2< x <4 .`
`text((i.e. the higher) \ x text(-value when) \ \ p^{′}(x) = 0)`
`text(At) \ \ x = ((8a + 4) + 4 sqrt(a^2 + a + 1))/(3a + 3) \ ,`
`text(S) text(olve for) \ \ a \ \ text(such that) \ \ p(x) = -4`
`=> a = 0.716 \ \ text((to 3 d.p.))`
f. `p(x) \ text(intersects) \ x text(-axis at) \ \ x = 4-(4)/(1 + a) = (4a)/(1 + a)`
| `A` | `= int_0^{(4a)/(1 +a)} p(x)\ dx-int_{(4a)/(1 +a)}^4 p(x)\ dx` |
| `= (64(1 + 2a + 2a^3 + a^4))/(3(1 + a)^4)` |
`text(S) text(olve) \ \ A^{′}(a) = 0 \ \ text(for) \ \ a :`
`a = 1`
g. `C(a) = 120\ 000 int_0^{(4a)/(1 +a)} p(x)\ dx-100\ 000 int_{(4a)/(1 +a)}^4 p(x)\ dx`
`text(S) text(olve) \ \ C^{′}(a) = 0 \ \ text(for) \ \ a :`
`a = 0.886 \ \ text((to 3 d.p.))`
The wind speed at a weather monitoring station varies according to the function
`v(t) = 20 + 16sin ((pi t)/(14))`
where `v` is the speed of the wind, in kilometres per hour (km/h), and `t` is the time, in minutes, after 9 am.
--- 3 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
A sudden wind change occurs at 10 am. From that point in time, the wind speed varies according to the new function
`v_1(t) = 28 + 18 sin((pi(t-k))/(7))`
where `v_1` is the speed of the wind, in kilometres per hour, `t` is the time, in minutes, after 9 am and `k ∈ R^+`. The wind speed after 9 am is shown in the diagram below.
--- 2 WORK AREA LINES (style=lined) ---
Using this value of `k`, the weather monitoring station sends a signal when the wind speed is greater than 38 km/h.
i. Find the value of `t` at which a signal is first sent, correct to two decimal places. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
ii. Find the proportion of one cycle, to the nearest whole percent, for which `v_1 > 38`. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
State the values of `a`, `b`, `c` and `d`, in terms of `k` where appropriate. (3 marks)
--- 11 WORK AREA LINES (style=lined) ---
`v_text(min) \ = 4 \ text(km/h)`
ii. `31text(%)`
a. `text(Amplitude) = 16`
`text{Find Period (n):}`
| `(2 pi)/(n)` | `= (pi)/(14)` |
| `n` | `= 28` |
b. `v_text(max) = 20 + 16 = 36 \ text(km/h)`
`v_text(min) = 20-16 = 4 \ text(km/h)`
| c. `v(60)` | `= 20 + 16 sin ((60 pi)/(14))` |
| `= 32.5093 \ \ text(km/h)` |
d. `v(t)\ \ text(is always positive.)`
`s(t) = int_0^60 v(t) \ dt`
| `v(t)_(avg)` | `= (1)/(60) int_0^60 20 + 16 sin ((pi t)/(14))\ dt` |
| `= 20.447` | |
| `= 20.45 \ text(km/h) \ \ text((to 2 d.p.))` |
e. `text(S) text{olve (for}\ k text{):} \ \ v(60) = v_1(60)`
`k = 3.4358 \ \ text((to 4 d.p.))`
f.i. `text(S) text(olve for) \ t , \ text(given) \ \ v_1(t) = 38 \ \ text(and) \ \ k = 31.4358`
`=> t = 60.75 \ text(minutes)`
f.ii. `text(S) text(olving for) \ \ v_1(t) = 38 \ , \ k = 31.4358`
`t_1 = 60.75 \ text{(part i)}, \ t_2 = 65.123`
`text(Period of) \ \ v_1 = (2 pi)/(n) = (pi)/(7)\ \ => \ n = 14`
| `:. \ text(Proportion of cycle)` | `= (65.123-60.75)/(14)` |
| `= 0.312` | |
| `= 31 text{% (nearest %)}` |
g. `f(x) → g(x)`
`y^{prime} = 28 + 18 sin ({pi(x^{prime}-k)}/{7})`
| `x^{prime} = ax + c` | `\ \ \ \ \ \ y^{prime} = by + d` |
`text(Using) \ \ y^{prime} = by + d`
`28 + 18 sin ({pi(x^{prime}-k)}/{7}) = b (20 + 16 sin ({pi x}/{14})) + d`
`text(Equating coefficients of) \ \ sin theta :`
`16b = 18 \ \ \ => \ b = (9)/(8)`
`text(Equating constants:)`
`20 xx (9)/(8) + d = 28 \ \ \ => \ \ d = (11)/(2)`
| `(x^{prime}-k)/(7)` | `= (x)/(14)` |
| `x^{prime}` | `= (x)/(2) + k \ \ => \ \ a = (1)/(2) \ , \ c = k` |
`a = (1)/(2) \ , \ b = (9)/(8) \ , \ c = k \ , \ d = (11)/(2)`
Let `f(x) = (ax + b)^5` and let `g` be the inverse function of `f`.
Given that `f(0) = 1`, what is the value of `g' (1)`
`C`
`f(x) = (ax + b)^5`
`text(Given) \ \ f(0) = 1\ \ =>\ \ b^5 = 1 \ => \ b = 1`
`f ‘(x) = 5a(ax + 1)^4`
`f(0) = 1 \ => \ g(1) = 0 \ \ text{(Inverse: swap} \ x ↔ y )`
`text(Gradient of) \ \ f(x) \ \ text(at) \ \ x =0 \ \ text(will be the reciprocal of the gradient of) \ \ g(x) \ \ text(at) \ \ x = 1`
`f ‘(0) = 5a`
`:. \ g'(1) = (1)/(5a)`
`=> \ C`
The shaded region in the diagram below is bounded by the vertical axis, the graph of the function with rule `f(x) = sin(pix)` and the horizontal line segment that meets the graph at `x = a`, where `1 <= a <= 3/2`.
Let `A(a)` be the area of the shaded region.
--- 6 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
a. `text(Lower border of shaded area:)\ y = f(a) = sin(a pi)`
| `text(Area)` | `= int_0^a sin(pi x)-sin (a pi)\ dx` |
| `= [-1/pi cos (pi x)-x sin(a pi)]_0^a` | |
| `= [-1/pi cos(pi a)-a sin (a pi)-(-1/pi-0)]` | |
| `= 1/pi-1/pi cos (a pi)-a sin(a pi)` |
b. `text(S) text(ince)\ 1 <= a <= 3/2,`
`A(1) = 1/pi-1/pi cos(pi)-1 sin (pi) = 2/pi`
`A(3/2) = 1/pi-1/pi cos ((3 pi)/2)-3/2 sin ((3pi)/2) = 1/pi + 3/2 = (2 + 3pi)/(2 pi)`
`:.\ text(Range:)\ \ [2/pi, (2 + 3pi)/(2 pi)]`
c.i. `A(a) = int_0^a sin(pi x)-sin (a pi)\ dx`
| `A_1` | `=2int _0^a sin(pi x) + sqrt 3/2\ dx` | |
| `=2int _0^a sin(pi x)-sin((4pi)/3)\ dx,\ \ \ (a=4/3)` | ||
| `=2int _0^(4/3) sin(pi x)-sin((4pi)/3)\ dx` | ||
| `=2 xx A(a)` |
`:.\ text(When)\ \ a = 4/3,\ \ text(Area) = 2 xx A(a)`
c.ii. `text(When)\ \ a = 4/3`
| `text(Area)` | `= 2 xx (1/pi-1/pi cos ((4 pi)/3)-4/3 sin ((4 pi)/3))` |
| `= 2 xx (1/pi + 1/(2 pi) + 4/3 xx sqrt 3/2)` | |
| `= 2(3/(2pi) + (2 sqrt 3)/3)` | |
| `= 3/pi + (4 sqrt 3)/3` | |
| `= (9 + 4 sqrt 3 pi)/(3 pi)` |
A pallet of bricks weighing 500 kg sits on a rough plane inclined at an angle of `α°` to the horizontal, where `tan(α°) = (7)/(24)`. The pallet is connected by a light inextensible cable that passes over a smooth pulley to a hanging container of mass `m` kilograms in which there is 10 L of water. The pallet of bricks is held in equilibrium by the tension `T` newtons in the cable and a frictional resistance force of 50 `g` newtons acting up and parallel to the plane. Take the weight force exerted by 1 L of water to be `g` newtons.
Suddenly the water is completely emptied from the container and the pallet of bricks begins to slide down the plane. The frictional resistance force of 50 `g` newtons acting up the plane continues to act on the pallet.
a.
b. `text(Resolving vertical forces on container:)`
`T – (m + 10)g = 0 \ …\ (1)`
`text(Resolving forces on plane:)`
`tan α = (7)/(24) \ => \ sin α = (7)/(25)`
`text(Solve for m:)`
| `(m + 10)g` | `= 500 text(g) · (7)/(25) – 50 text(g)` |
| `m + 10` | `= 140 – 50` |
| `:. \ m` | `= 80` |
c. `text(Resolving vertical forces on container:)`
`T – 80 g = 80 a \ …\ (1)`
`text(Resolving forces on plane:)`
`500 g sin α – (T + 50 g) = 500 a`
`90 g – T = 500 a \ …\ (2)`
`text(Add) \ (1) + (2)`
| `10 g` | `= 580 a` |
| `a` | `= (g)/(58)` |
| `s` | `= ut + (1)/(2) at^2` |
| `= 0 + (1)/(2) · (g)/(58) + 10^2` | |
| `= (25g)/(29)` |
d.i. `m = 80 + 2t`
d.ii. `text(Resolving vertical forces on container:)`
`T – (80+2t)g = (80+2t)a \ …\ (1)`
`text(Resolving forces on plane:)`
`90g – T = 500a \ …\ (2)`
`text(Add)\ (1) + (2)`
| `(90 – 80 – 2t)g` | `= (500 + 80 + 2t)a` |
| `(10 – 2t)g` | `=(580 + 2t)a` |
| `a` | `= (g(5 – t))/(t + 290) ms^-2` |
d.iii. `(dv)/(dt) = (g(5 – t))/(t + 290)`
`v = int (dv)/(dt)\ dt = 295 log_e ((t + 290)/(290)) – g t + c`
`text(When)\ t = 0, v = 3\ \ text{(given)} \ => \ c = 3`
`:. \ v = 295 log_e ((t+290)/(290)) – g t + 3`
`:. \ v(4) = 3.4\ text(ms)^-1`
A canon ball is fired from a castle wall across a horizontal plane at `V` ms−1.
Its position vector `t` seconds after it is fired from its origin is given by `underset~s(t) = V tunderset~i - 1/2g t^2 underset~j`.
--- 5 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
i. `text(Time of flight ⇒ find)\ t\ text(when)\ \ y = −h`
| `−1/2g t^2` | `= −h` |
| `t^2` | `= (2h)/g` |
| `t` | `= sqrt((2h)/g),\ \ t > 0` |
`text(S)text(ince the canon ball impacts when)\ \ x = 8h:`
| `Vt` | `= 8h` |
| `Vsqrt((2h)/g)` | `= 8h` |
| `V` | `= (8sqrt(hg))/sqrt2` |
| `= 4sqrt(2hg)` |
ii. `underset~v = 4sqrt(2hg) underset~i – g t underset~j`
| `|underset~v|` | `= sqrt((4sqrt(2hg))^2 + (−g t)^2)` |
| `= sqrt(16 xx 2hg + g^2 t^2)` | |
| `=sqrt(g(32h + g t^2)` |
| `text(Distance)` | `= int_0^sqrt((2h)/g) |underset~v|\ dt` |
| `= int_0^sqrt((2h)/g) sqrt(g(32h + g t^2))\ dt` |
A snowboarder at the Winter Olympics leaves a ski jump at an angle of `theta` degrees to the horizontal, rises up in the air, performs various tricks and then lands at a distance down a straight slope that makes an angle of 45° to the horizontal, as shown below.
Let the origin `O` of a cartesian coordinate system be at the point where the snowboarder leaves the jump, with a unit vector in the positive `x` direction being represented by `underset~i` and a unit vector in the positive `y` direction being represented by `underset~j`. Distances are measured in metres and time is measured in seconds.
The position vector of the snowboarder `t` seconds after leaving the jump is given by
`underset~r (t) = (6t-0.01t^3) underset~i + (6 sqrt3 t-4.9t^2 + 0.01t^3) underset~j , \ t ≥ 0`
--- 5 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
a. `v(t) = (6-0.03t^2)underset~i + (6 sqrt3-9.8t + 0.03t^2) underset~j`
`text(When) \ t =0,`
`v(t) = 6underset~i + 6 sqrt3 underset~j`
`tan theta = (6 sqrt3)/(6) = sqrt3`
| `:. \ theta` | `= tan^-1 sqrt3= 60°` |
| b. | `text(Speed)` | `= |v(0)|` |
| `= sqrt(6^2 + (6 sqrt3)^2)` | ||
| `= 12 \ text(ms)^-1` |
c. `text(Max height when) \ underset~j \ text(component of) \ v(t) = 0`
`text(Solve): \ \ 6 sqrt3-9.8t + 0.03t^2 = 0`
`=> t = 1.064 \ text(seconds)`
| `text(Max height)` | `= 6 sqrt3 (1.064)-4.9(1.064)^2 + 0.01(1.064)^3` | |
| `~~5.5\ text(m)` |
d. `text(Time of Flight ⇒ Solve for)\ \ t\ \ text(when)\ \ y=-x:`
| `6 sqrt 3 t-4.9t^2 + 0.01 t^3` | `= -(6t-0.01t^3)` |
| `(6 + 6 sqrt3)t-4.9 t^2` | `= 0` |
| `t(6 + 6 sqrt3-4.9 t)` | `= 0` |
| `4.9 t` | `= 6 + 6 sqrt3` |
| `t` | `= (6 + 6 sqrt3)/(4.9)` |
| `= (60(sqrt3 + 1))/(49)\ text(seconds)` |
A snowboarder at the Winter Olympics leaves a ski jump at an angle of `theta` degrees to the horizontal, rises up in the air, performs various tricks and then lands at a distance down a straight slope that makes an angle of 45° to the horizontal, as shown below.
Let the origin `O` of a cartesian coordinate system be at the point where the snowboarder leaves the jump, with a unit vector in the positive `x` direction being represented by `underset~i` and a unit vector in the positive `y` direction being represented by `underset~j`. Distances are measured in metres and time is measured in seconds.
The position vector of the snowboarder `t` seconds after leaving the jump is given by
`underset~r (t) = (6t-0.01t^3) underset~i + (6 sqrt3 t-4.9t^2 + 0.01t^3) underset~j , \ t ≥ 0`
--- 4 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
a. `v(t) = (6-0.03t^2)underset~i + (6 sqrt3-9.8t + 0.03t^2) underset~j`
`text(When) \ t =0,`
`v(t) = 6underset~i + 6 sqrt3 underset~j`
`tan theta = (6 sqrt3)/(6) = sqrt3`
| `:. \ theta` | `= tan^-1 sqrt3` |
| `= 60°` |
| b. | `text(Speed)` | `= |v(0)|` |
| `= sqrt(6^2 + (6 sqrt3)^2)` | ||
| `= 12 \ text(ms)^-1` |
c. `text(Max height when) \ underset~j \ text(component of) \ v(t) = 0`
`text(Solve): \ \ 6 sqrt3-9.8t + 0.03t^2 = 0`
`=> t = 1.064 \ text(seconds)`
| `text(Max height)` | `= 6 sqrt3 (1.064)-4.9(1.064)^2 + 0.01(1.064)^3` | |
| `~~5.5\ text(m)` |
d. `text(Time of Flight ⇒ Solve for)\ \ t\ \ text(when)\ \ y=-x:`
| `6 sqrt 3 t-4.9t^2 + 0.01 t^3` | `= -(6t-0.001t^3)` |
| `(6 + 6 sqrt3)t-4.9 t^2` | `= 0` |
| `t(6 + 6 sqrt3-4.9 t)` | `= 0` |
| `4.9 t` | `= 6 + 6 sqrt3` |
| `t` | `= (6 + 6 sqrt3)/(4.9)` |
| `= (60(sqrt3 + 1))/(49)\ text(seconds)` |
e. `text(Total distance) \ = text(Area under) \ v(t) \ text(graph from)\ \ t = 0 \ \ text(to)\ \ t_1 = (60(sqrt3 + 1))/(49)`
`|v(t)| = sqrt{(6-0.03 t^2)^2 + (6 sqrt3- 9.8t + 0.03 t^2)^2}`
| `text(Distance)` | `= int_0^(t_1) |v(t)| \ dt` |
| `= 38.51 \ text{m (to 2 d.p.)}` |
A ship sails 6 km from `A` to `B` on a bearing of 121°. It then sails 9 km to `C`. The
size of angle `ABC` is 114°.
Copy the diagram into your writing booklet and show all the information on it.
--- 2 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
--- 6 WORK AREA LINES (style=lined) ---
| i. |  |
`text(Let point)\ D\ text(be due North of point)\ B`
| `/_ABD` | `=180-121\ text{(cointerior with}\ \ /_A text{)}` |
| `=59^@` | |
| `/_DBC` | `=114-59` |
| `=55^@` |
`:. text(Bearing of)\ \ C\ \ text(from)\ \ B\ \ text(is)\ 055^@`
ii. `text(Using cosine rule:)`
| `AC^2` | `=AB^2+BC^2-2xxABxxBCxxcos/_ABC` |
| `=6^2+9^2-2xx6xx9xxcos114^@` | |
| `=160.9275…` | |
| `:.AC` | `=12.685…\ \ \ text{(Noting}\ AC>0 text{)}` |
| `=13\ text(km)\ text{(nearest km)}` |
iii. `text(Need to find)\ /_ACB\ \ \ text{(see diagram)}`
| `cos/_ACB` | `=(AC^2+BC^2-AB^2)/(2xxACxxBC)` |
| `=((12.685…)^2+9^2-6^2)/(2xx(12.685..)xx9)` | |
| `=0.9018…` | |
| `/_ACB` | `=25.6^@\ text{(to 1 d.p.)}` |
`text(From diagram,)`
`/_BCE=55^@\ text{(alternate angle,}\ DB\ text(||)\ CE text{)}`
`:.\ text(Bearing of)\ A\ text(from)\ C`
| `=180+55+25.6` | |
| `=260.6` | |
| `=261^@\ text{(nearest degree)}` |
Members of the association will travel to a conference in cars and minibuses:
The constraints above can be represented by the following three inequalities.
`text(Inequality 1) qquad qquad x + y <= 8`
`text(Inequality 2) qquad qquad x >= 3`
`text(Inequality 3) qquad qquad y >= 2`
A maximum of 60 people can attend the conference.
Use this information to write Inequality 4. (1 mark)
The graph below shows the four lines representing Inequalities 1 to 4.
Also shown on this graph are four of the integer points that satisfy Inequalities 1 to 4. Each of these integer points is marked with a cross (✖).
Each car will cost $70 to hire and each minibus will cost $100 to hire.
The cost of hiring each minibus remained $100.
All original constraints apply.
If the increase in the cost of hiring each car is more than `k` dollars, then the maximum cost of transporting members to this conference can only occur when using six cars and two minibuses.
Determine the value of `k`. (1 mark)
a. `5x + 10y <= 60`
| b. |
c. `text(Consider the line)\ \ 5x + 10y = 60\ \ text(on the graph)`
`text(Touches the feasible region at)\ (4, 4)\ text(only)`
`:.\ text (C) text(ost of 60 members)`
`= 4 xx 70 + 4 xx 100`
`= $680`
d. `text(Coordinates that allow 55 to travel) \ => \ (5, 3) and (3, 4)`
`text(C) text(ost)\ (5, 3) = 5 xx 70 + 3 xx 100 = $650`
`text(C) text(ost)\ (3, 4) = 3 xx 70 + 4 xx 100 = $610`
`:.\ text(Minimum cost is $610)`
e. `text(Objective function): \ C = ax + 100y`
`text(Max cost occurs at)\ \ (6, 2)\ \ text(when)\ \ a > 100`
`text{(i.e. graphically when the slope of}\ \ C = ax + 100y`
`text(is steeper than)\ \ x + y= 8 text{)}`
| `:. k + 70` | `= 100` |
| `k` | `= 30` |
The following diagram shows a crane that is used to transfer shipping containers between the port and the cargo ship.
The length of the boom, `BC`, is 25 m. The length of the hoist, `AB`, is 15 m.
Round your answer to the nearest degree. (1 mark)
The base of the crane (`Q`) is 20 m from a shipping container at point `R`. The shipping container will be moved to point `P`, 38 m from `Q`. The crane rotates 120° as it moves the shipping container anticlockwise from `R` to `P`.
What is the distance `RP`, in metres?
Round your answer to the nearest metre. (1 mark)
Four chains connect the shipping container to a hoist at point `M`, as shown in the diagram below.
The shipping container has a height of 2.6 m, a width of 2.4 m and a length of 6 m.
Each chain on the hoist is 4.4 m in length.
What is the vertical distance, in metres, between point `M` and the top of the shipping container?
Round your answer to the nearest metre. (2 marks)
| a.i. | `AC` | `= sqrt(BC^2 – AB^2)` |
| `= sqrt(25^2 – 15^2)` | ||
| `= sqrt 400` | ||
| `= 20` |
| a.ii. | `tan\ /_ ACB` | `= 15/20` |
| `/_ ACB` | `= tan^(-1) (3/4)` | |
| `= 36.86…` | ||
| `~~ 37^@` |
b. `text(Using cosine rule:)`
| `RP^2` | `= 20^2 + 38^2 – 2 xx 20 xx 38 xx cos 120^@` |
| `= 2604` | |
| `:. RP` | `= 51.029…` |
| `~~ 51\ text(metres)` |
| c. |
`text(Find)\ h => text(need to find)\ x`
`text(Consider the top of the container)`
| `x` | `= sqrt(3^2 + 1.2^2)` |
| `~~ 3.2311` |
| `:. h` | `= sqrt(4.4^2 – 3.2311^2)` |
| `= 2.98…` | |
| `~~ 3\ text(metres)` |
Fencedale High School is planning to renovate its gymnasium.
This project involves 12 activities, `A` to `L`.
The directed network below shows these activities and their completion times, in weeks.
The minimum completion time for the project is 35 weeks.
--- 2 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
It is possible to reduce the completion time for activities `C, D, G, H` and `K` by employing more workers.
What is the minimum time, in weeks, that the renovation project could take? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
a. `text(Scanning forwards and backwards:)`
`text(Critical path:)\ ABDFGIKL`
`:. 8\ text(activities)`
b. `text(LST for activity)\ E = 12\ text{weeks (i.e. start of 13th week)}`
c. `text(Consider float times of all activities not on critical path.)`
`J-5, H-1, E-1, C-1`
`:.\ text(Activity)\ J\ text(has the largest float time.)`
d. `text(Critical path after reducing)\ CDGHK\ text(by 2 weeks is)`
`ABDFGIKL.`
| `:.\ text(Minimum time)` | `= 2 + 4 + 7 + 1 + 2 + 2 + 5 + 6` |
| `= 29\ text(weeks)` |
Fencedale High School is planning to renovate its gymnasium.
This project involves 12 activities, `A` to `L`.
The directed network below shows these activities and their completion times, in weeks.
The minimum completion time for the project is 35 weeks.
--- 4 WORK AREA LINES (style=lined) ---
--- 1 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
It is possible to reduce the completion time for activities `C, D, G, H` and `K` by employing more workers.
What is the minimum time, in weeks, that the renovation project could take? (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
The table below shows the five activities that can have their completion times reduced and the associated weekly cost, in dollars.
| Activity | Weekly cost ($) |
| `C` | 3000 |
| `D` | 2000 |
| `G` | 2500 |
| `H` | 1000 |
| `K` | 4000 |
The completion time for each of these five activities can be reduced by a maximum of two weeks.
Fencedale High School requires the overall completion time for the renovation project to be reduced by four weeks at minimum cost.
Complete the table below, showing the reductions in individual activity completion times that would achieve this. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
| Activity | Reduction in completion time (0, 1 or 2 weeks) |
| `C` | |
| `D` | |
| `G` | |
| `H` | |
| `K` |
| Activity | Reduction in completion time (0, 1 or 2 weeks) |
|
| `C` | 0 | |
| `D` | 1 | |
| `G` | 2 | |
| `H` | 1 | |
| `K` | 1 |
a. `text(Scanning forwards and backwards:)`
`text(Crirical path:)\ ABDFGIKL`
`:. 8\ text(activities)`
b. `text(LST for activity)\ E = 12\ text{weeks (i.e. start of 13th week)}`
c. `text(Consider float times of all activities not on critical path.)`
`J-5, H-1, E-1, C-1`
`:.\ text(Activity)\ J\ text(has the largest float time.)`
d. `text(Critical path after reducing)\ CDGHK\ text(by 2 weeks is)`
`ABDFGIKL.`
| `:.\ text(Minimum time)` | `= 2 + 4 + 7 + 1 + 2 + 2 + 5 + 6` |
| `= 29\ text(weeks)` |
e. `text(Reduce cheapest activities on the critical path by 1 week)`
`↓ 1 =>\ text(Activity)\ D\ text(and)\ G`
`text{Possibilities for reducing by a further week (choose 2)}`
`C and D:\ text(cost $5000)\ \ text{(too expensive)}`
`G and H:\ text(cost $3500)\ \ text{(yes)}`
`K:\ text(cost $4000)\ \ text{(yes)}`
| Activity | Reduction in completion time (0, 1 or 2 weeks) |
|
| `C` | 0 | |
| `D` | 1 | |
| `G` | 2 | |
| `H` | 1 | |
| `K` | 1 |
On Sunday, matrix `V` is used when calculating the expected number of visitors at each location every hour after 10 am. It is assumed that the park will be at its capacity of 2000 visitors for all of Sunday.
Let `L_0` be the state matrix that shows the number of visitors at each location at 10 am on Sunday.
The number of visitors expected at each location at 11 am on Sunday can be determined by the matrix product
`{:(qquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquad text(this hour)),(qquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquadqquad qquad qquad \ A qquad quad F qquad \ G \ quad quad W),({:V xx L_0 qquad text(where) qquad L_0 = [(500), (600), (500), (400)]{:(A),(F),(G),(W):}, qquad text(and):} qquad V = [(0.3,0.4,0.6,0.3),(0.1,0.2,0.1,0.2),(0.1,0.2,0.2,0.1),(0.5,0.2,0.1,0.4)]{:(A),(F),(G),(W):}\ text(next hour)):}`
--- 3 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
| a. | `text{By inspection (higher decimal values in row 1)}` | |
| `=>\ text(test location)\ A` | ||
| `text(Visitors at)\ A\ text{(11 am)}` | `= 0.3 xx 500 + 0.4 xx 600 + 0.6 xx 500 + 0.3 xx 400` | |
| `= 810` | ||
`text(Location)\ A\ text(will have more than 600 visitors.)`
| b.i. | `VR_0` | `= [(0.3,0.4,0.6,0.3),(0.1,0.2,0.1,0.2),(0.1,0.2,0.2,0.1),(0.5,0.2,0.1,0.4)][(500),(600),(500),(400)]=[(810),(300),(310),(580)]` |
| `R_1` | `= V xx R_0 + B_1` | |
| `= [(810),(300),(310),(580)] + [(-210),(0),(210),(0)]` | ||
| `:. B_1` | `= [(-210),(0),(210),(0)]` |
| b.ii. | `R_2` | `= [(0.3,0.4,0.6,0.3),(0.1,0.2,0.1,0.2),(0.1,0.2,0.2,0.1),(0.5,0.2,0.1,0.4)][(600),(300),(520),(580)] + B_2` |
| `= [(786),(288),(282),(644)] + [(-186),(0),(230),(-44)]= [(600),(288),(512),(600)]` |
A museum is planning an exhibition using five rooms.
The museum manager draws a network to help plan the exhibition. The vertices `A`, `B`, `C`, `D` and `E` represent the five rooms. The number on the edges represent the maximum number of people per hour who can pass through the security checkpoints between the rooms.
--- 2 WORK AREA LINES (style=lined) ---
Draw the minimum cut onto the network below and recommend a change that the manager could make to one or more security checkpoints to increase the flow capacity to 240 visitors per hour. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
| a. | `text(Capacity)` | `= 130 + 90 + 70` |
| `= 290` |
COMMENT: In part (a), edge BC flows from the exit to the entry and is therefore not counted.
b. `text(Maximum flow capacity:)`
`text(Minimum cut = 80 + 40 + 65 + 45 = 230)`
COMMENT: In part (b), edge BC now flows from entry to exit in the new “minimum” cut and is counted.
`text(If security is improved to increase the flow)`
`text(between Room C and Room B by 10 visitors)`
`text(per hour, the network’s flow capacity increases)`
`text(to 240.)`
A company produces packets of noodles. It is known from past experience that the mass of a packet of noodles produced by one of the company's machines is normally distributed with a mean of 375 grams and a standard deviation of 15 grams.
To check the operation of the machine after some repairs, the company's quality control employees select two independent random samples of 50 packets and calculate the mean mass of the 50 packets for each random sample.
--- 5 WORK AREA LINES (style=lined) ---
--- 5 WORK AREA LINES (style=lined) ---
To test whether the machine is working properly after the repairs and is still producing packets with a mean mass of 375 grams, the two random samples are combined and the mean mass of the 100 packets is found to be 372 grams. Assume that the standard deviation of the mass of the packets produced is still 15 grams. A two-tailed test at the 5% level of significance is to be carried out.
--- 1 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
a. `barX\ ~\ N(375, (15/sqrt50)^2)`
`text(Pr)(370 <= barX <= 375)`
`= 0.490788…`
`text(Pr)(text(not in range)) ~~ 1-0.490788 ~~ 0.509212`
`text(Pr)(text(Samples within range) >= 1)`
`= 1-text(Pr)(text(0 samples in range))`
`~~ 1-(0.509212)^2`
`~~ 0.741`
b. `text(Let)\ \ Y = barX_1-barX_2`
`Y\ ~\ N (0, 2 xx (15^2)/50)`
`text(Pr)(−2 < Y < 2)\ \ (text(by CAS))`
`= text(norm cdf)\ (−2,2,0, sqrt(2 xx (15^2)/50))`
`~~ 0.495`
c. `H_0: \ mu = 375`
`H_1: \ mu != 375`
d. `text(By CAS:)\ \ mu_0 = 375, \ barx = 372, \ sigma = 15, \ n = 100`
`p ~~ 0.046`
e. `p < 0.05 \ => \ text(reject)\ H_0`
`=>\ text(The machine is NOT working properly.)`
f. `text(Pr)(barx <= a) = 0.025\ \ (text(2 sided test))`
| `a_text(min)` | `= text(inv norm)\ (0.025, 375, 15/sqrt100)` |
| `= 372.06…` | |
| `=372.1` |
A mass of `m_1` kilograms is initially held at rest near the bottom of a smooth plane inclined at `theta` degrees to the horizontal. It is connected to a mass of `m_2` kilograms by a light inextensible string parallel to the plane, which passes over a smooth pulley at the end of the plane. The mass `m_2` is 2 m above the horizontal floor.
The situation is shown in the diagram below.
• weight forces `W_1` and `W_2`
• the normal reaction force `N`
• the tension in the string `T`
On the diagram above, show and clearly label the forces acting on each of the masses. (1 mark)
| a. |
b. `T = m_2g\ \ … \ (1)`
`T = m_1sin(theta)\ \ … \ (2)`
`text{Solve: (1) = (2)}`
| `m_1g sin(theta)` | `= m_2g` |
| `sin(theta)` | `= (m_2)/(m_1)` |
c.i. `m_2g > m_1gsin(theta)`
`sin(theta) < (m_2)/(m_1)`
`theta < sin^(−1)\ ((m_2)/(m_1)), \ \ theta ∈ (0, pi/2)`
c.ii. `text(Net force)\ (F) = m_2g – m_1gsin(theta)`
| `(m_1 + m_2) · a` | `= g(m_2 – m_1 sin(theta))` |
| `:. a` | `= (g(m_2 – m_1 sin(theta)))/(m_1 + m_2)` |
d. `text(Motion:)\ m_1\ text(will accelerate up the plane for 2 m.)`
`m_1\ text(will then decelerate up plane until)\ v = 0.`
`text(Find)\ v_(m_1)\ \ text(given)\ \ s_(m_1) = 2, \ u = 0, \ m_1=2m_2`
`a = (g(m_2 – m_1 sintheta))/(m_1 + m_2) = (g(m_2 – 2m_2 · 1/4))/(2m_2 + m_2) = g/6`
`text(Using)\ \ v^2 = u^2 + 2as,`
`v_(m_1)^2 = 0 + 2 · g/6 · 2 = (2g)/3`
`text(Find distance)\ (s_2)\ text(for)\ m_1\ text(to decelerate until)\ v = 0:`
`a = −gsintheta = −g/4, \ u = sqrt((2g)/3)`
| `0` | `= (2g)/3 – 2 · g/4 · s_2` |
| `s_2` | `= (2g)/3 xx 2/g` |
| `= 4/3` |
| `:.\ text(Maximum distance)` | `= 2 + 4/3` |
| `= 10/3\ text(m)` |
--- 3 WORK AREA LINES (style=lined) ---
--- 0 WORK AREA LINES (style=lined) ---
Let `|z + m| = n`, where `m, n ∈ R`, represent the circle of minimum radius that passes through the solutions of `2z^2 + 4z + 5 = 0`.
--- 3 WORK AREA LINES (style=lined) ---
--- 2 WORK AREA LINES (style=lined) ---
--- 0 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
Let `|z + p| = q` represent the circle of minimum radius in the complex plane that passes through these solutions, where `a, b, c, p, q ∈ R`.
Find `p` and `q` in terms of `a, b` and `c`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
| a.i. | `z` | `= (−b ± sqrt(b^2-4ac))/(2a)` |
| `= (−4 ± sqrt(16-4 · 2 · 5))/(4)` | ||
| `= (−4 ± 2sqrt6 i)/(4)` | ||
| `= −1 ± sqrt6/2 i\ \ …\ text(as required)` |
| a.ii. |
b.i. `text(Radius of circle = )sqrt6/2`
`text(Centre) = (0, −1)`
`:. m = 1, \ n = sqrt6/2`
| b.ii. | `|z + 1|` | `= sqrt6/2` |
| `|x + iy + 1|` | `= sqrt6/2` | |
| `(x + 1)^2 + y^2` | `= 3/2` |
| b.iii. |
c. `text(Solve:)\ 2z^2 + 4z + d = 0`
`z = −1 ± sqrt(4-2d)/2 = −1 ± sqrt((2-d)/2)`
`z + 1 = ± sqrt((2-d)/2)`
`text(Solve for)\ d\ text(such that:)`
`|sqrt((2-d)/2)| <= sqrt6/2`
`−1 <= d <= 5\ \ (text(by CAS))`
d. `z = (−b ± sqrt(b^2-4ac))/(2a) = (−b)/(2a) ± sqrt(b^2-4ac)/(2a)`
| `z + b/(2a)` | `= ± sqrt(b^2-4ac)/(2a)` |
| `|z + b/(2a)|` | `= |sqrt(b^2-4ac)/(2a)|` |
`:. p = b/(2a), \ q = |sqrt(b^2-4ac)/(2a)|`
Let `f: R -> R, \ f(x) = 1-x^3`. The tangent to the graph of `f` at `x = a`, where `0 < a < 1`, intersects the graph of `f` again at `P` and intersects the horizontal axis at `Q`. The shaded regions shown in the diagram below are bounded by the graph of `f`, its tangent at `x = a` and the horizontal axis.
--- 3 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
Let `A` be the function that determines the total area of the shaded regions.
--- 5 WORK AREA LINES (style=lined) ---
--- 3 WORK AREA LINES (style=lined) ---
Consider the regions bounded by the graph of `f^(-1)`, the tangent to the graph of `f^(-1)` at `x = b`, where `0 < b < 1`, and the vertical axis.
--- 4 WORK AREA LINES (style=lined) ---
--- 4 WORK AREA LINES (style=lined) ---
a. `f(x) = 1-x^3,\ \ f^{\prime}(x) = -3x^2`
`m_text(tang) = -3a^2\ \ text(through)\ \ (a, 1-a^3)`
`y = 2a^3-3a^2x + 1`
b. `text(Solve for)\ \x:`
`2a^3-3a^2x + 1 = 0`
`x = (2a^3 + 1)/(3a^2)`
c. `text(Solve for)\ \ x:`
`2a^3-3a^2x + 1 = 1-x^3`
`x=-2a`
`:. x text(-coordinate of)\ P = -2a`
d. `P(-2a, 8a^3 + 1),\ \ Q((2a^3 + 1)/(3a^2), 0)`
| `A` | `= text(Area of triangle)-int_(-2a)^1 f(x)\ dx` |
| `= 1/2((2a^3 + 1)/(3a^2) + 2a)(8a^3 + 1)-int_(-2a)^1 1-x^3\ dx` | |
| `= (80a^6 + 8a^3-9a^2 + 2)/(12a^2)\ \ text{(by CAS)}` |
e. `text(Solve for)\ a: \ (dA)/(da) = 0\ \ text{(by CAS)}`
`a = 10^(-1/3)`
f. `text(Consider)\ f(x):\ \ f(10^(-1/3)) = 9/10`
`A_text(min)\ text(for)\ \ f(x)\ \ text(occurs at)\ \ (10^(-1/3), 9/10)`
`=> A_text(min)\ text(for)\ \ f^(-1)(x)\ \ text(occurs when)\ \ x=9/10`
`:. b = 9/10`
g. `f^{\prime} (1) = -3`
`text(Gradient of)\ \ f^(-1)(x)\ \ text(at)\ \ x = 1\ \ text(is vertical line.)`
| `tan theta` | `= 1/3` |
| `theta` | `= tan^(-1)(1/3)` |
| `=18.4°\ \ text{(to 1 d.p.)}` |
The Lorenz birdwing is the largest butterfly in Town A. The probability density function that describes its life span, `X`, in weeks, is given by `f(x) = {(4/625 (5x^3-x^4), quad 0 <= x <= 5),(0, quad text(elsewhere)):}` --- 3 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- The wingspans of Lorenz birdwing butterflies in Town A are normally distributed with a mean of 14.1 cm and a standard deviation of 2.1 cm. --- 2 WORK AREA LINES (style=lined) --- Find the greatest possible wingspan, in centimetres, for a very small Lorenz birdwing butterfly in Town A, correct to one decimal place. (1 mark) --- 4 WORK AREA LINES (style=lined) --- Each year, a detailed study is conducted on a random sample of 36 Lorenz birdwing butterflies in Town A. A Lorenz birdwing butterfly is considered to be very large if its wingspan is greater than 17.5 cm. The probability that the wingspan of any Lorenz birdwing butterfly in Town A is greater than 17.5 cm is 0.0527, correct to four decimal places. --- 2 WORK AREA LINES (style=lined) --- Find the smallest value of `n`, where `n` is an integer. (2 marks) --- 5 WORK AREA LINES (style=lined) --- --- 2 WORK AREA LINES (style=lined) --- --- 5 WORK AREA LINES (style=lined) --- In a particular sample of Lorenz birdwing butterflies from Town B, an approximate 95% confidence interval for the proportion of butterflies that are very large was calculated to be (0.0234, 0.0866), correct to four decimal places. Determine the sample size used in the calculation of this confidence interval. (2 marks) --- 5 WORK AREA LINES (style=lined) ---
d. `W\ ~\ N (14.1, 2.1^2)` `text(Pr)(16 < W < 18) = 0.1512\ \ \ text{(by CAS)}` e. `text(Solution 1:)` `text(Pr)(W < w) = 0.05` `text(Pr)(Z < z) = 0.05\ \ =>\ \ z = -1.6449\ \ text{(by CAS)}` `text(invNorm)` `text(Tail setting: left)` `text(prob: 0.05)` `sigma: 2.1` `mu: 14.1` `=> 10.6\ \ \ text{cm (by CAS)}` f.i. `L\ ~\ text(Bi)(n, p)\ ~\ text(Bi) (36, 0.0527)` `text(Pr)(L >= 3) ~~ 0.2947` `text(CAS: binomialCdf) (x, 36, 36, 0.0527)` `text(Pr)(L >= 0) = 0.011 > 0.01` `text(Pr)(L >= 7) = 0.002 < 0.01` `:.\ text(Smallest)\ n = 7` f.iv. `hat p +- 1 sigma: (0.0527-0.0372, 0.0527 + 0.0372) = (0.0155, 0.0899)` `text(Pr)(0.0155 < hat p < 0.0899)` `= text(Pr)(36 xx 0.0155 < L < 36 xx 0.0899)` `= text(Pr)(0.56 < L < 3.24)` `= text(Pr)(1 <= L <= 3)` `~~ 0.7380` g. `0.0234 = hat p-1.96 sqrt((hat p(1-hat p))/n) qquad text{… (1)}` `0.0866 = hat p + 1.96 sqrt((hat p(1-hat p))/n) qquad text{… (2)}` `text(Solve simultaneous equations:)` `hat p ~~ 0.055, quad n ~~ 199.96` `:.\ text(Sample size) = 200`
a.
`mu`
`= 4/625 int_0^5 x(5x^3-x^4)\ dx`
`= 4/625[x^5-1/6 x^6]_0^5`
`= 10/3\ \ \ text{(by CAS)}`
b.
`text(Pr)(X > 2)`
`= 4/625 int_2^5 5x^3-x^4\ dx`
`= 4/625[5/4x^4-x^5/5]_2^5`
`= 0.9129…`
`:.\ text(Expected number)`
`= 80 xx 0.9129…`
`~~ 73.03`
`~~ 73`
c.
`text(Pr)(X = 4|X> 2)`
`= (text(Pr)(X >= 4))/(text(Pr)(X >= 2))`
`= 0.26272/0.91296`
`= 0.2878`
`(w-14.1)/2.1`
`= -1.6449`
`w`
`= 10.6\ text(cm)`
`text(Solution 2:)`
f.ii.
`text(Pr)(L >= n) < 0.01`
f.iii.
`E(hat p)`
`= p = 0.0527`
`sigma(hat p)`
`= sqrt((p(1-p))/n) = sqrt((0.0527(1-0.0527))/36) ~~ 0.0372`