SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

Calculus, MET1 2008 ADV 3b

  1. Differentiate  `log_e(cos x)` with respect to `x`.   (2 marks)

  2. Hence, or otherwise, evaluate  `int_0^(pi/4) tan x\ dx`.   (2 marks)

Show Answers Only
  1. `-tan x`
  2. `-log_e(1/sqrt2)\  text{or  0.35  (2 d.p.)}`
Show Worked Solution
a.   `y` `= log_e(cos x)`
  `(dy)/(dx)` `= (-sin x)/(cos x)`
    `=-tan x`

 

b.   `int_0^(pi/4) tan x\ dx`

`= -[log_e(cos x)]_0^(pi/4)`

`= -[log_e(cos(pi/4))-log_e(cos 0)]`

`= -[log_e(1/sqrt2)-log_e 1]`

`= -[log_e(1/sqrt2)-0]`

`= -log_e(1/sqrt2)`

`= 0.346…`

`= 0.35\ \ (text(2 d.p.))`

Calculus, MET1 2016 ADV 12d

  1. Differentiate  `y = xe^(3x)`.   (1 mark)

  2. Hence find the exact value of  `int_0^2 e^(3x) (3 + 9x)\ dx`.   (2 marks)

Show Answers Only
  1. `e^(3x) (1 + 3x)`
  2. `6e^6`
Show Worked Solution

a.  `y = xe^(3x)`

`text(Using product rule,)`

`(dy)/(dx)` `= x · 3e^(3x) + 1 · e^(3x)`
  `= e^(3x) (1 + 3x)`

 

b.  `int_0^2 e^(3x) (3 + 9x)\ dx`

`= 3 int_0^2 e^(3x) (1 + 3x)\ dx`

`= 3 [x e^(3x)]_0^2`

`= 3 (2e^6-0)`

`= 6e^6`

Calculus, MET1 SM-Bank 5

The diagram shows the graph of the function  `f: (0,oo) →R,`  where  `f(x) = 1/x`.

The area under  `f(x)`  between  `x = a` and  `x = 1`  is `A_1`. The area under the curve between  `x = 1` and  `x = b` is `A_2`.

The areas `A_1` and `A_2` are each equal to 1 square unit.

Find the values of `a` and `b`.  (3 marks)

Show Answers Only

`a = 1/e`

`b = e`

Show Worked Solution
`int_a^1 1/x dx` `= 1`
`[ln x]_a^1` `= 1`
`ln 1 – ln a` `= 1`
`ln a` `= −1`
`:. a` `= e^(−1) = 1/e`

 

`int_1^b 1/x dx` `= 1`
`[ln x]_1^b` `= 1`
`ln b – ln 1` `= 1`
`ln b` `= 1`
`:. b` `= e`

Calculus, MET1 SM-Bank 4

The curves  `y = e^(2x)` and  `y = e^(−x)` intersect at the point `(0,1)` as shown in the diagram.

Find the exact area enclosed by the curves and the line  `x = 2`.  (3 marks)

Show Answers Only

`1/2 e^4 + e^(−2) – 3/2\ \ \ text(u²)`

Show Worked Solution

Note: there’s marker’s comment in this part

`text(Area)` `= int_0^2 e^(2x)\ \ dx – int_0^2 e^(−x)\ \ dx`
  `= int_0^2 (e^(2x) – e^(−x))dx`
  `= [1/2 e^(2x) + e^(−x)]_0^2`
  `= [(1/2 e^4 – e^(−2)) – (1/2 e^0 + e^0)]`
  `= 1/2 e^4 + e^(−2) – 3/2\ \ \ text(u²)`

Calculus, MET1 SM-Bank 3

For the function  `f:R→R,\ \ f(x)= 2e^x + 3x`, determine the coordinates of the point  `P`  at which the tangent to  `f(x)`  is parallel to the line  `y = 5x - 3`.   (3 marks)

Show Answers Only

`(0, 2)`

Show Worked Solution

`y = 5x-3\ \ =>\ m=5`

`y` `= 2e^x + 3x`
`(dy)/(dx)` `= 2e^x + 3`

  
`text(Find)\ \ x\ \ text(when)\ \ (dy)/(dx) = 5,`

`5` `= 2e^x + 3`
`2e^x` `= 2`
`e^x` `= 1`
`x` `= 0`

  
`text(When)\ \ x = 0,`

`y` `= 2e^0 + (3 xx 0)=2`

  
`:.P\ \ text{has coordinates (0, 2)}`

Algebra, MET1 SM-Bank 9

Solve the following equation for `x`:

`2e^(2x) - e^x = 0`.  (2 marks)

Show Answers Only

`x = ln\ 1/2`

Show Worked Solution

`text(Solution 1)`

`2e^(2x) – e^x = 0`

`text(Let)\ \ X = e^x`

`2X^2 – X` `= 0`
`X (2X – 1)` `= 0`

 
`X = 0 or 1/2`
 

`text(When)\ \ e^x = 0\  =>\ text(no solution)`

`text(When)\ \ e^x = 1/2`

`ln e^x` `= ln\ 1/2`
`:. x` `= ln\ 1/2`

 

`text(Solution 2)`

`2e^(2x)-e^x` `=0`
`2e^(2x)` `=e^x`
`ln 2e^(2x)` `=ln e^x`
`ln 2 +ln e^(2x)` `=x`
`ln 2 + 2x` `=x`
`x` `=-ln2`
  `=ln\ 1/2`

Algebra, MET1 SM-Bank 8

Write `log2 + log4 + log8 + log16 + … + log128`  in the form  `a logb`  where `a` and `b` are integers greater than 1.  (2 marks)

Show Answers Only

`28log2`

Show Worked Solution

`log2 + log4 + log8 + … + log 128`

`= log2^1 + log2^2 + log2^3 + … + log2^7`

`= log2 + 2log2 + 3log2 + … + 7log2`

`= 28log2`

Probability, MET1 2016 VCAA 7

A company produces motors for refrigerators. There are two assembly lines, Line A and Line B. 5% of the motors assembled on Line A are faulty and 8% of the motors assembled on Line B are faulty. In one hour, 40 motors are produced from Line A and 50 motors are produced from Line B. At the end of an hour, one motor is selected at random from all the motors that have been produced during that hour.

  1. What is the probability that the selected motor is faulty? Express your answer in the form `1/b`, where `b` is a positive integer.  (2 marks)

  2. The selected motor is found to be faulty.
  3. What is the probability that it was assembled on Line A? Express your answer in the form `1/c`, where `c` is a positive integer.  (1 mark)

Show Answers Only

  1. `1/15`
  2. `1/3`

Show Worked Solution

a.   `text(Construct tree diagram)`

`text(Pr)(AF) + text(Pr)(BF)`

`= 4/9 xx 1/20 + 5/9 xx 2/25`

`= 1/45 + 2/45`

`= 1/15`
 

`:. text(Pr)(F) = 1/15`

 

♦♦ Mean mark 32%.

b.    `text(Pr)(A|F)` `= (text(Pr)(A ∩ F))/(text(Pr)(F))`
    `= (4/9 xx 1/20)/(1/15)`
    `= 1/45 xx 15`
    `= 1/3`

Graphs, MET1 2016 VCAA 5

Let  `f : (0, ∞) → R`, where  `f(x) = log_e(x)`  and  `g: R → R`, where  `g (x) = x^2 + 1`.

  1.   i. Find the rule for `h`, where  `h(x) = f (g(x))`.   (1 mark)

    ii. State the domain and range of `h`.   (2 marks)

  2. iii. Show that  `h(x) + h(-x) = f ((g(x))^2 )`.   (2 marks)

  3. iv. Find the coordinates of the stationary point of `h` and state its nature.   (2 marks)

     

  4. Let  `k: (-∞, 0] → R`  where  `k (x) = log_e(x^2 + 1)`.
  5.  i. Find the rule for  `k^(-1)`.   (2 marks)

  6. ii. State the domain and range of  `k^(-1)`.   (2 marks)

Show Answers Only
  1.   i. `log_e(x^2 + 1)`
  2.  ii. `[0,∞)`
  3. iii. `text(See Worked Solutions)`
  4. iv. `(0, 0)`
  5.  i. `-sqrt(e^x-1)`
  6. ii. `text(Domain)\ (k) = (-∞,0]`
  7.    `text(Range)\ (k) = [0,∞)`
Show Worked Solution
a.i.    `h(x)` `= f(x^2 + 1)`
    `= log_e(x^2 + 1)`

 

a.ii.   `text(Domain)\ (h) =\ text(Domain)\ (g) = R`

♦♦ Mean mark part (a)(ii) 30%.
  `text(For)\ x ∈ R` `-> x^2 + 1 >= 1`
  `-> log_e(x^2 + 1) >= 0`

`:.\ text(Range)\ (h) = [0,∞)`

 

MARKER’S COMMENT: Many students were unsure of how to present their working in this question. Note the layout in the solution.
a.iii.   `text(LHS)` `= h(x) + h(−x)`
    `= log_e(x^2 _ 1) + log_e((-x)^2 + 1)`
    `= log_e(x^2 + 1) + log_e(x^2 + 1)`
    `= 2log_e(x^2 + 1)`

 

`text(RHS)` `= f((x^2 + 1)^2)`
  `= 2log_e(x^2 + 1)`

 

`:. h(x) + h(-x) = f((g(x))^2)\ \ text(… as required)`

 

a.iv.   `text(Stationary points when)\ \ h^{prime}(x) = 0`

♦ Mean mark part (a)(iv) 41%.
MARKER’S COMMENT: Solving a fraction is zero

   `text(Using Chain Rule:)`

`h^{prime}(x)` `= (2x)/(x^2 + 1)`

`:.\ text(S.P. when)\ \ x=0`

 

`text(Find nature using 1st derivative test:)`

`:.\ text{Minimum stationary point at (0, 0)}.`

 

b.i.   `text(Let)\ \ y = k(x)`

♦ Mean mark (b)(i) 49%.
MARKER’s COMMENT: Many students failed to consider the restrictions on the domain in `k(x)` and only select the negative root.

  `text(Inverse: swap)\ x ↔ y`

`x` `= log_e(y^2 + 1)`
`e^x` `= y^2 + 1`
`y^2` `= e^x-1`
`y` `= ±sqrt(e^x-1)`

 

`text(But range)\ \ (k^(-1)) =\ text(domain)\ (k)`

`:.k^(-1)(x) =-sqrt(e^x-1)`

♦ Mean mark part (b)(ii) 44%.

 

b.ii.   `text(Range)\ (k^(-1)) =\ text(Domain)\ (k) = (-∞,0]`

  `text(Domain)\ (k^(-1)) =\ text(Range)\ (k) = [0,∞)`

Probability, MET1 2016 VCAA 4

A paddock contains 10 tagged sheep and 20 untagged sheep. Four times each day, one sheep is selected at random from the paddock, placed in an observation area and studied, and then returned to the paddock.

  1. What is the probability that the number of tagged sheep selected on a given day is zero?  (1 mark)

  2. What is the probability that at least one tagged sheep is selected on a given day?  (1 mark)

  3. What is the probability that no tagged sheep are selected on each of six consecutive days?
  4. Express your answer in the form `(a/b)^c`, where `a`, `b` and `c` are positive integers.  (1 mark)

Show Answers Only

  1. `16/81`
  2. `65/81`
  3. `(2/3)^24`

Show Worked Solution

a.   `text(Let)\ \ X =\ text(Number of tagged sheep,)`

`X ~\ text(Bi)(4,1/3)`

`text(Pr)(X = 0)` `= ((4),(0)) xx (1/3)^0 xx (2/3)^4`
  `= 16/81`

 

b.    `text(Pr)(X >= 1)` `= 1 – text(Pr)(X = 0)`
    `= 1 – 16/81`
    `= 65/81`

 

c.   `text(Let)\ \ Y =\ text(Days that no tagged sheep selected,)`

`Y ~\ text(Bi)(6,16/81)`

`text(Pr)(Y = 6)` `= ((6),(6)) xx (16/81)^6 xx (65/81)^0`
  `= (16/81)^6 = (2/3)^24`

Calculus, MET1 2016 VCAA 3

Let  `f: R text{\}{1} -> R`  where  `f(x) = 2 + 3/(x - 1)`.

  1. Sketch the graph of  `f`. Label the axis intercepts with their coordinates and label any asymptotes with the appropriate equation.   (3 marks)
     

     

  2. Find the area enclosed by the graph of  `f`, the lines  `x = 2`  and  `x = 4`, and the `x`-axis.   (2 marks)

Show Answers Only
  1.  
  2. `4 + 3log_e(3)\ text(units)`
Show Worked Solution
a.   

 

b.    `text(Area)` `= int_2^4 2 + 3(x – 1)^(−1)\ dx`
    `= [2x + 3 log_e(x – 1)]_2^4`
    `= (8 + 3log_e(3)) – (4 + 3log_e(1))`
    `= 4 + 3log_e(3)\ \ text(u²)`

Calculus, MET1 2016 VCAA 2

Let  `f: (-∞,1/2] -> R`, where  `f(x) = sqrt(1-2x)`.

  1. Find  `f^{prime}(x)`.   (1 mark)

  2. Find the angle `theta` from the positive direction of the `x`-axis to the tangent to the graph of  `f` at  `x =-1`, measured in the anticlockwise direction.   (2 marks)

Show Answers Only
  1. `(-1)/(sqrt(1-2x))`
  2. `(5pi)/6`
Show Worked Solution
a.    `f(x)` `= (1-2x)^(1/2)`
  `f^{prime}(x)` `= 1/2(1-2x)^(-1/2) (-2)qquadtext([Using Chain Rule])`
    `= (-1)/(sqrt(1-2x))`

 

♦ Mean mark 40%.
b.    `tan theta` `= f^{prime}(-1)`
    `= (-1)/(sqrt(1-2(-1)))`
    `= (-1)/(sqrt3)`

 

`text(S)text(ince)\ theta ∈ [0,pi],`

`=> theta = (5pi)/6`

Calculus, MET2 2009 VCAA 2

VCAA 2009 2a

A train is travelling at a constant speed of `w` km/h along a straight level track from `M` towards `Q.`

The train will travel along a section of track `MNPQ.`

Section `MN` passes along a bridge over a valley.

Section `NP` passes through a tunnel in a mountain.

Section `PQ` is 6.2 km long.

From `M` to `P`, the curve of the valley and the mountain, directly below and above the train track, is modelled by the graph of
 

`y = 1/200 (ax^3 + bx^2 + c)` where `a, b` and `c` are real numbers.
 

All measurements are in kilometres.

  1. The curve defined from `M` to `P` passes through `N (2, 0)`. The gradient of the curve at `N` is – 0.06 and the curve has a turning point at  `x = 4`.
  2.  i. From this information write down three simultaneous equations in `a`, `b` and `c`.   (3 marks)

  3. ii. Hence show that  `a = 1`, `b = – 6` and `c = 16`.   (2 marks)

  4. Find, giving exact values
  5.   i. the coordinates of `M and P`.   (2 marks)

  6.  ii. the length of the tunnel.   (1 mark)

  7. iii. the maximum depth of the valley below the train track.   (1 mark)

The driver sees a large rock on the track at a point `Q`, 6.2 km from `P`. The driver puts on the brakes at the instant that the front of the train comes out of the tunnel at `P`.

From its initial speed of `w` km/h, the train slows down from point `P` so that its speed `v` km/h is given by

`v = k log_e ({(d + 1)}/7)`,

where `d` km is the distance of the front of the train from `P` and `k` is a real constant.

  1. Find the value of `k` in terms of `w`.   (1 mark)

  2. Find the exact distance from the front of the train to the large rock when the train finally stops.   (2 marks)

Show Answers Only

a.i.    `1/200 (8a + 4b + c) = 0`

a.ii.   `1/200 (12a + 4b) = (– 3)/50`

a.iii.  `1/200 (48a + 8b) = 0`

`text(Proof)\ \ text{(See Worked Solutions)}`

    1. `M (2 + 2 sqrt 3, 0),\ \ P (2-2 sqrt 3, 0)`
    2. `2 sqrt 3\ text(km)`
    3. `2/25\ text(km)`
  2. `(– w)/(log_e (7))`
  3. `120`
  4. `0.2\ text(km)`
Show Worked Solution

 a.i.   `N (2, 0),`

`1/200 (8a + 4b + c) = 0\ \ text{… (1)}`
 

`(dy)/(dx) (x = 2) = (– 3)/50,`

`1/200 (12a + 4b) = (– 3)/50\ \ text{… (2)}`
 

`(dy)/(dx)(x = 4) = 0,`

`1/200 (48a + 8b) = 0\ \ text{… (3)}`
 

  ii.   `text(Using the above equations,)`

♦ Mean mark part (a)(ii) 41%.
`12a + 4b` `=-12` `\ \ \ …\ (2^{′})`
`24 a + 4b` `=0` `\ \ \ …\ (3^{′})`

 
`text{Solve simultaneous equations (By CAS):}`

`a=1, \ b=-6, \ c=16`
 

`\text{Solving manually:}`

`(3^{′})-(2^{′}):`

`12a=12 \ \Rightarrow\ \ a=1`

`text(Substitute)\ \ a = 1\ \ text(into)\ \ (3^{′}):`

`124(1)+4b=0 \ \Rightarrow\ \ b=-1`

`text(Substitute)\ \ a = 1,\ \ b = – 6\ \ text(into)\ \ (1):`

`8(1) + 4 (– 6) + c=0\ \ \Rightarrow\ \ c=16`
 

b.i.   `text(For)\ \ x text(-intercepts),`

`text(Solve:)\ \ x^3 + -6x^2 + 16` `= 0\ \ text(for)\ x,`
 `x= 2-2 sqrt 3, 2, 2 + 2 sqrt 3`  

 
`:. M (2 + 2 sqrt 3, 0),\ \ P (2-2 sqrt 3, 0)`
 

  ii.   `N (2, 0)`

♦ Mean mark part (a) 41%.
`bar (NP)` `=\ text(Tunnel length)`
  `= 2-(2-2 sqrt 3)`
  `= 2 sqrt 3\ text(km)`

 

   iii.  `text(Solve)\ \ frac (dy) (dx) = 0\ \ text(for)\ \ x in (2, 2 + 2 sqrt 3)`

♦ Mean mark part (b) 50%.

`x = 4`

`text(When)\ \ x=4,\ \ y = – 2/25\ text(km) = 80\ text{m (below track)}`

`:.\ text(Max depth below is)\ \ 80\ text(m.)`
 

c.  `text(Solution 1)`

♦ Mean mark part (c) 35%.

`text(Let)\ \ v(d) = k log_e ({(d + 1)}/7)`

`text(S)text(ince)\ \ v=w\ \ text(when)\ \ d=0\ \ text{(given),}`

`k log_e ({(0 + 1)}/7)` `=w`
`k` `=w/log_e (1/7)`
  `=(-w)/log_e7`

 
`text(Solution 2)`

`text(Solve:)\ \ v (0)` `= w\ \ text(for)\ \ k`
`:. k` `= (– w)/(log_e (7))`

 

d.  `v (2.5) = k log_e(1/2)`

♦ Mean mark part (d) 40%.
`text(Solve)\ \ v(2.5)` `= (120 log_e (2))/(log_e (7))\ \ text(for)\ \ k,`
`:. k` `= (– 120)/(log_e (7))`
`(– w)/(log_e (7))` `= (– 120)/(log_e (7))`
`:. w` `= 120`

 

e.   `text(Define)\ \ v (d) = (– 120)/(log_e (7)) log_e ((d + 1)/7)`

♦♦ Mean mark part (e) 32%.
`text(Solve:)\ \ v(d)` `= 0\ \ text(for)\ d,`
`:. d` `= 6\ text(km from)\ \ P`

 
`:.\ text(Distance between train and)\ \ Q`

`= 6.2-6`

`= 0.2\ text(km)`

Calculus, MET2 2009 VCAA 1

Let  `f: R^+ uu {0} -> R,\ f(x) = 6 sqrt x-x-5.`

The graph of  `y = f (x)`  is shown below.

VCAA 2009 1a

  1. State the interval for which the graph of `f` is strictly decreasing.   (2 marks)

  2. Points `A` and `B` are the points of intersection of  `y = f (x)`  with the `x`-axis. Point `A` has coordinates `(1, 0)` and point `B` has coordinates `(25, 0)`.

     

    Find the length of `AD` such that the area of rectangle `ABCD` is equal to the area of the shaded region.   (2 marks)
     
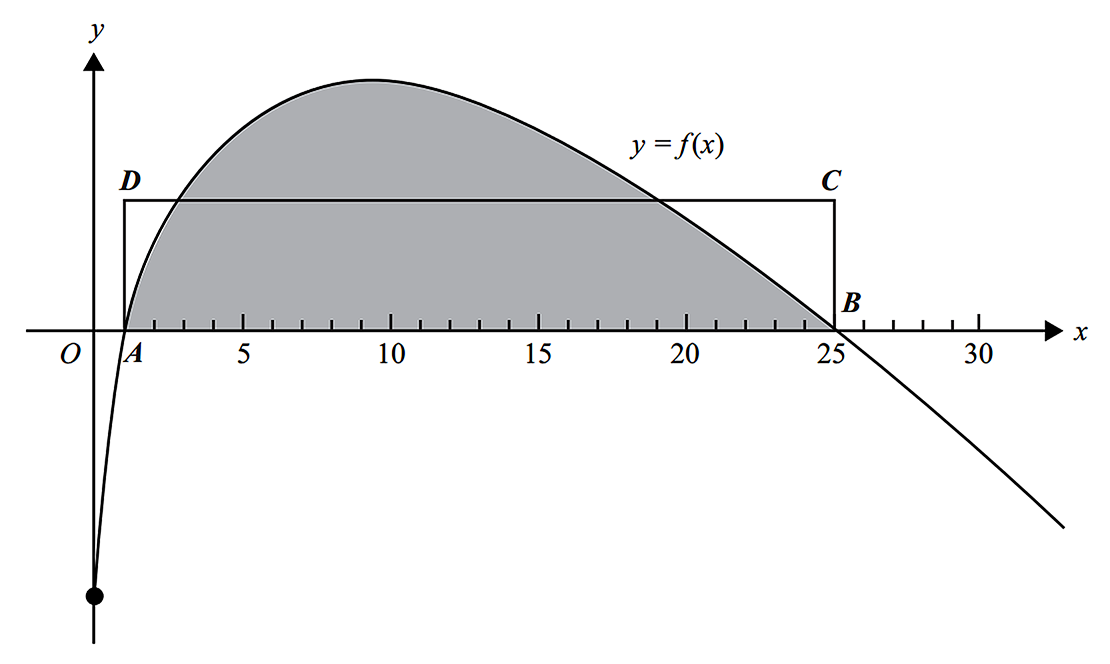
    VCAA 2009 1c

  3. The points `P (16, 3)` and `B (25, 0)` are labelled on the diagram.

      
     

          VCAA 2009 1d

     

    1. Find `m`, the gradient of the chord `PB`.   (Exact value to be given.)   (1 mark)

    2. Find  `a in [16, 25]`  such that  `f prime (a) = m`.  (Exact value to be given.)   (2 marks)

Show Answers Only

a.  `x in [9,oo)`

b.  `8/3`

c.i.   `m=-1/3`

c.ii.  `a=81/4`

Show Worked Solution
a.   vcaa-2009-1ai
`text(Stationary point when)\ \ f^{′}(x)` `= 0`
`x` `= 9`

 
`:.\ text(Strictly decreasing for)\ \ x in [9, oo)`

 

b.   vcaa-2009-1ci
`AD` `= y_text(average)`
  `= 1/(25-1) int_1^25\ f(x)\ dx`
  `= 8/3\ \ text{[by CAS]}`

 

c.i.   `m_(PB)` `= (3-0)/(16-25)`
  `:. m_(PB)` `=-1/3`

 

 c.ii.   `text(Solve)\ \ f^{′}(a)` `= -1/3\ \ text(for)\ \ a in [16, 25]`
  `:. a` `= 81/4`

Graphs, MET2 2009 VCAA 19 MC

The graph of a function  `f`, with domain `R`, is as shown.

VCAA 2009 19mc

The graph which best represents  `1 - f (2x)`  is

VCAA 2009 19mci

VCAA 2009 19mcii

Show Answers Only

`E`

Show Worked Solution

`text(Determine transformations)`

`text(from)\ \ f -> – f (2x) + 1`

`text(- Dilate by factor)\ 1/2\ text(from)\ y text(-axis.)`

`text(- Reflect in)\ x text(-axis.)`

`text(- Shift up 1 unit.)`

`=>   E`

Calculus, MET2 2009 VCAA 18 MC

The average value of the function  `f: R\ text(\){text(−)1/2} -> R,\ f(x) = 1/(2x + 1)`  over the interval  `[0, k]`  is  `1/6 log_e (7).`

The value of `k` is

  1. `(-6)/(log_e(7)) - 1/2`
  2. `3`
  3. `e^3`
  4. `(-log_e(7))/(2(log_e(7) + 6))`
  5. `171`
Show Answers Only

`B`

Show Worked Solution
`text(Solve:)\ \ 1/(k-0) int_0^k 1/(2x + 1)\ dx` `= 1/6 log_e (7)`
`text(for)\ \ k` `> 0`

`:. k = 3`

`=>   B`

Algebra, MET2 2009 VCAA 16 MC

The inverse of the function  `f: R^+ -> R,\ f(x) = e^(2x + 3)`  is

  1. `{:(f^-1:\ R^+ -> R, qquad qquad qquad qquad f^-1 (x) = e^(-2x - 3)):}`
  2. `{:(f^-1:\ R^+ -> R, qquad qquad qquad qquad f^-1 (x) = e^((x - 3)/2)):}`
  3. `{:(f^-1:\ (e^3, oo) -> R, qquad qquad f^-1 (x) = log_e (sqrt x) - 3/2):}`
  4. `{:(f^-1:\ (e^3, oo) -> R, qquad qquad f^-1 (x) = e^((x - 3)/2)):}`
  5. `{:(f^-1:\ (e^3, oo) -> R, qquad qquad f^-1 (x) = -log_e (2x - 3)):}`
Show Answers Only

`C`

Show Worked Solution

`text(Let)\ \ y = f(x)`

`text(Inverse:  swap)\ \ x harr y`

`x` `=e^(2y + 3)`
`log_e x` `=2y+3`
`2y` `=log_e x -3`
`y` `=1/2 log_e (x) – 3/2`

 
`:. f^-1 (x) = log_e (sqrt x) – 3/2`

`=>   C`

Calculus, MET2 2009 VCAA 15 MC

For  `y = sqrt (1 - f(x)),\ \ (dy)/(dx)`  is equal to

A.   `(2 f prime (x))/(sqrt(1 - f(x))`

B.   `(-1)/(2 sqrt (1 - f prime (x)))`

C.   `1/2 sqrt (1 - f prime (x))`

D.   `3/(2(1 - f prime(x)))`

E.   `(-f prime (x))/(2 sqrt (1 - f (x)))`

Show Answers Only

`E`

Show Worked Solution

`text(Using Chain Rule,)`

`dy/dx` `= – f′(x) xx 1/2 xx (1-f(x))^(- 1/2)`
  `=(- f′(x))/(2 sqrt (1 – f (x)))`

`=>   E`

Probability, MET2 2009 VCAA 13 MC

A fair coin is tossed twelve times.

The probability (correct to four decimal places) that at most 4 heads are obtained is

A.   `0.0730`

B.   `0.1209`

C.   `0.1938`

D.   `0.8062`

E.   `0.9270`

Show Answers Only

`C`

Show Worked Solution

`text(Let)\ \ X = text(Number of heads),`

`X∼\ text(Bi) (12, 1/2)`

`text(Pr) (X <= 4) ~~ 0.1938\ \ [text(CAS: binomCdf) (12, 1/2, 0, 4)]`

`=>   C`

Graphs, MET2 2009 VCAA 12 MC

A transformation  `T: R^2 -> R^2`  that maps the curve with equation  `y = sin (x)`  onto the curve with equation  `y = 1 - 3 sin(2x + pi)`  is given by

  1. `T [(x), (y)] = [(2, 0), (0, -3)] [(x), (y)] + [(pi), (1)]`
  2. `T [(x), (y)] = [(– 1/2, 0), (0, 3)] [(x), (y)] + [(pi/2), (1)]`
  3. `T [(x), (y)] = [(0, – 3), (2, 0)] [(x), (y)] - [(pi), (1)]`
  4. `T [(x), (y)] = [(1/2, 0), (0, – 3)] [(x), (y)] + [(– pi/2), (1)]`
  5. `T [(x), (y)] = [(1/2, 0), (0, 3)] [(x), (y)] + [(– pi/2), (– 1)]`
Show Answers Only

`D`

Show Worked Solution

`text(Let)\ \ f(x) = sin (x)`

`text(Let)\ \ g(x) = – 3 sin (2 (x + pi/2)) + 1`

`text(Find transformations taking)\ \ f -> g`

 

`3 f (2x) = 3 sin (2x) = h(x)`

`– h(x) = – 3 sin (2x) = k(x)`

`k (x + pi/2) + 1 = – 3 sin (2 (x + pi/2)) + 1 = g(x)`

 

`text(Dilate by factor 3 from)\ \ x text(-axis)`

`text(Dilate by factor)\ \ 1/2\ \ text(from)\ \ y text(-axis)`

`text(Reflect in)\ \ x text(-axis)`

`text(Translate left)\ \ pi/2\ \ text(up 1)`

`=>   D`

Probability, MET2 2009 VCAA 11 MC

The continuous random variable `X` has a probability density function given by
 

`f(x) = {(pi sin (2 pi x), text(if)\ \ 0 <= x <= 1/2), (0, text(elsewhere)):}`
 

The value of `a` such that  `text(Pr) (X > a) = 0.2`  is closest to

  1. `0.26`
  2. `0.30`
  3. `0.32`
  4. `0.35`
  5. `0.40`
Show Answers Only

`D`

Show Worked Solution
`text(Solve)\ \ int_a^(1/2) f (x)\ dx` `= 0.2,\ \ a in [0, 1/2]`
`:. a` `~~ 0.35`

`=>   D`

Probability, MET2 2009 VCAA 6 MC

The continuous random variable `X` has a normal distribution with mean 14 and standard deviation 2.

If the random variable `Z` has the standard normal distribution, then the probability that `X` is greater than 17 is equal to

  1. `text(Pr) (Z > 3)`
  2. `text(Pr) (Z < 2)`
  3. `text(Pr) (Z < 1.5)`
  4. `text(Pr) (Z < – 1.5)`
  5. `text(Pr) (Z > 2)`
Show Answers Only

`D`

Show Worked Solution
`text(Pr) (X > 17)` `= text(Pr) (Z > (17 – 14)/2)`
  `= text(Pr) (Z > 1.5)`
  `= text(Pr) (Z < – 1.5)`

`=>   D`

Algebra, MET2 2009 VCAA 5 MC

Let  `f: R -> R,\ f (x) = x^2`

Which one of the following is not true?

  1. `f(xy) = f (x) f (y)`
  2. `f(x) - f(-x) = 0`
  3. `f (2x) = 4 f (x)`
  4. `f (x - y) = f(x) - f(y)`
  5. `f (x + y) + f (x - y) = 2 (f (x) + f(y))`
Show Answers Only

`D`

Show Worked Solution

`text(Solution 1)`

`text(Consider option)\ D:`

`f(x-y)` `=(x-y)^2`
  `=x^2 -2xy+y^2`
`f(x)-f(y)` `= x^2-y^2`
`:.f(x-y)` `!=f(x)-f(y)`

 
`=>D`

 

`text(Solution 2)`

`text(Define)\ \ f(x) = x^2`

`text(Enter each functional equation on CAS)`

`text(until output does NOT read “true”.)`

`=>   D`

Algebra, MET2 2009 VCAA 4 MC

The general solution to the equation  `sin (2x) = -1`  is

  1. `x = n pi - pi/4,\ n in Z`
  2. `x = 2n pi + pi/4 or x = 2n pi - pi/4,\ n in Z`
  3. `x = (n pi)/2 + (-1)^n pi/2,\ n in Z`
  4. `x = (n pi)/2 + (-1)^n pi/4,\ n in Z`
  5. `x = n pi + pi/4 or x = 2n pi + pi/4,\ n in Z`
Show Answers Only

`A`

Show Worked Solution
`2x` `= 2n pi – pi/2,\ \ n in Z`
`x` `= n pi – pi/4,\ \ n in Z`

 
`=>   A`

Calculus, MET2 2011 VCAA 4

Deep in the South American jungle, Tasmania Jones has been working to help the Quetzacotl tribe to get drinking water from the very salty water of the Parabolic River. The river follows the curve with equation  `y = x^2-1`,  `x >= 0` as shown below. All lengths are measured in kilometres.

Tasmania has his camp site at `(0, 0)` and the Quetzacotl tribe’s village is at `(0, 1)`. Tasmania builds a desalination plant, which is connected to the village by a straight pipeline.
 

met2-2011-vcaa-q4

  1. If the desalination plant is at the point `(m, n)` show that the length, `L` kilometres, of the straight pipeline that carries the water from the desalination plant to the village is given by
  2.    `L = sqrt(m^4-3m^2 + 4)`.   (3 marks)

  3. If the desalination plant is built at the point on the river that is closest to the village
    1. find `(dL)/(dm)` and hence find the coordinates of the desalination plant.   (3 marks)

    2. find the length, in kilometres, of the pipeline from the desalination plant to the village.   (2 marks)

The desalination plant is actually built at `(sqrt7/2, 3/4)`.

If the desalination plant stops working, Tasmania needs to get to the plant in the minimum time.

Tasmania runs in a straight line from his camp to a point `(x,y)` on the river bank where  `x <= sqrt7/2`. He then swims up the river to the desalination plant.

Tasmania runs from his camp to the river at 2 km per hour. The time that he takes to swim to the desalination plant is proportional to the difference between the `y`-coordinates of the desalination plant and the point where he enters the river.

  1. Show that the total time taken to get to the desalination plant is given by

     

    `qquadT = 1/2 sqrt(x^4-x^2 + 1) + 1/4k(7-4x^2)` hours where `k` is a positive constant of proportionality.   (3 marks)

The value of `k` varies from day to day depending on the weather conditions.

  1. If  `k = 1/(2sqrt13)`
    1. find `(dT)/(dx)`   (1 mark)

    2. hence find the coordinates of the point where Tasmania should reach the river if he is to get to the desalination plant in the minimum time.   (2 marks)

  2. On one particular day, the value of `k` is such that Tasmania should run directly from his camp to the point `(1,0)` on the river to get to the desalination plant in the minimum time. Find the value of `k` on that particular day.   (2 marks)

  3. Find the values of `k` for which Tasmania should run directly from his camp towards the desalination plant to reach it in the minimum time.   (2 marks)

Show Answers Only
  1. `text(See Worked Solutions)`
  2.  i. `(sqrt6/2, 1/2)`
  3. ii. `sqrt7/2\ text(km)`
  4. `text(See Worked Solutions)`
  5.  i. `(dT)/(dx) = (x(2x^2-1))/(2sqrt(x^4-x^2 + 1))-(sqrt13 x)/13`
  6. ii. `(sqrt3/2, −1/4)`
  7. `1/4`
  8. `(5sqrt37)/74`
Show Worked Solution

a.   `text(S)text(ince)\ \ (m,n)\ \ text(lies on)\ \ y=x^2-1,`

♦ Mean mark (a) 47%.

`=> n=m^2-1`

`V(0,1), D(m,m^2-1)`

`L` `= sqrt((m-0)^2 + ((m^2-1)-1)^2)`
  `= sqrt(m^2 + m^4-4m^2 + 4)`
  `= sqrt(m^4-3m^2 + 4)\ \ text(… as required)`

 

b.i.   `(dL)/(dm) = (2m^2-3m)/(sqrt(m^4-3m^2 + 4))`

`text(Solve:)\ \ (dL)/(dm) = 0quadtext(for)quadm >= 0`

`\Rightarrow m = sqrt6/2`

`text(Substitute into:)\ \ D(m, m^2-1),`

`:. text(Desalination plant at)\ \ (sqrt6/2, 1/2)`
 

♦ Mean mark part (b)(ii) 41%.
b.ii.   `L(sqrt6/2)` `= sqrt(m^4-3m^2 + 4)`
    `=sqrt(36/16-3xx6/4+4`
    `=sqrt7/2`

 

c.   `text(Let)\ \ P(x,x^2-1)\ text(be run point on bank)`

♦♦♦ Mean mark (c) 16%.

`text(Let)\ \ D(sqrt7/2, 3/4)\ text(be desalination location)`

`T` `=\ text(run time + swim time)`
  `= (sqrt((x-0)^2 + ((x^2-1)-0)^2))/2 + k(3/4-(x^2-1))`
  `= (sqrt(x^2 + x^4-2x^2 + 1))/2 + k/4(3-4(x^2-1))`
`:. T` `= (sqrt(x^4-x^2 + 1))/2 + 1/4k(7-4x^2)`

 

d.i.   `(dT)/(dx) = (x(2x^2-1))/(2sqrt(x^4-x^2 + 1))-(sqrt13 x)/13`

 

d.ii.   `text(Solve:)\ \ (dT)/(dx) = 0`

♦♦ Mean mark (d.ii.) 33%.

`x = sqrt3/2`

`y=x^2-1=-1/4`

`:. T_(text(min)) \ text(when point is)\ \ (sqrt3/2, −1/4)`

 

e.  `(dT)/(dx) = (x(2x^2-1))/(2sqrt(x^4-x^2 + 1))-2kx`

♦♦ Mean mark (e) 39%.

`text(When)\ \ x=1:`

`text(Solve:)\ \ (dT)/(dx)` `=0\ \ text(for)\ k,`
`1/2 -2k` `=0`
`:.k` `=1/4`

 

f.   `text(Require)\ T_text(min)\ text(to occur at right-hand endpoint)\ \ x = sqrt7/2.`

`text(This can occur in 2 situations:)`

♦♦♦ Mean mark (f) 13%.

`text(Firstly,)\ \ T\ text(has a local min at)\ \ x = sqrt7/2,`

`text(Solve:)\ \ (x(2x^2-1))/(2sqrt(x^4-x^2 + 1))-2kx=0| x = sqrt7/2,\ \ text(for)\ k,`

`:.k = (5sqrt37)/74`
 

`text(S)text(econdly,)\ \ T\ text(is decreasing function over)\ x ∈ (0, sqrt7/2),`

`text(Solve:)\ \ (dT)/(dx) <= 0 | x = sqrt7/2,\ text(for)\ k,`

`:. k > (5sqrt37)/74`

`:. k >= (5sqrt37)/74`

Calculus, MET2 2011 VCAA 3

  1. Consider the function  `f: R -> R, f(x) = 4x^3 + 5x-9`.

     

    1. Find  `f^{prime}(x).`   (1 mark)

    2. Explain why  `f^{prime}(x) >= 5` for all `x`.   (1 mark)

  2. The cubic function `p` is defined by  `p: R -> R, p(x) = ax^3 + bx^2 + cx + k`, where `a`, `b`, `c` and `k` are real numbers.

     

    1. If `p` has `m` stationary points, what possible values can `m` have?   (1 mark)

    2. If `p` has an inverse function, what possible values can `m` have?   (1 mark)

  3. The cubic function `q` is defined by  `q:R -> R, q(x) = 3-2x^3`.

     

    1. Write down a expression for  `q^(-1)(x)`.   (2 marks)

    2. Determine the coordinates of the point(s) of intersection of the graphs of  `y = q(x)`  and  `y = q^(-1)(x)`.   (2 marks)

  4. The cubic function `g` is defined by  `g: R -> R, g(x) = x^3 + 2x^2 + cx + k`, where `c` and `k` are real numbers.

     

    1. If `g` has exactly one stationary point, find the value of `c`.   (3 marks)

    2. If this stationary point occurs at a point of intersection of  `y = g(x)`  and  `g^(−1)(x)`, find the value of `k`.   (3 marks)

Show Answers Only
    1. `f^{prime}(x) = 12x^2 + 5`
    2. `text(See Worked Solutions)`
    1. `m = 0, 1, 2`
    2. `m = 0, 1`
    1. `q^(-1)(x) = root(3)((3-x)/2), x ∈ R`
    2. `(1, 1)`
    1. `4/3`
    2. `-10/27`
Show Worked Solution

a.i.   `f^{prime}(x) = 12x^2 + 5`
  

a.ii.  `text(S)text(ince)\ \ x^2>=0\ \ text(for all)\ x,`

♦ Mean mark 47%.
` 12x^2` `>= 0`
`12x^2 + 5` `>=  5`
`f^{prime}(x)` `>=  5\ \ text(for all)\ x`

 

b.i.   `p(x) = text(is a cubic)`

♦♦♦ Mean mark part (b)(i) 9%, and part (b)(ii) 20%.
MARKER’S COMMENT: Good exam strategy should point students to investigate earlier parts for direction. Here, part (a) clearly sheds light on a solution!

`:. m = 0, 1, 2`

`text{(Note: part a.ii shows that a cubic may have no SP’s.)}`

 

b.ii.   `text(For)\ p^(−1)(x)\ text(to exist)`

`:. m = 0, 1`

 

c.i.   `text(Let)\ y = q(x)`

`text(Inverse: swap)\ x ↔ y`

`x` `= 3-2y^3`
`y^3` `= (3-x)/2`

`:. q^(-1)(x) = root(3)((3-x)/2), \ x ∈ R`
  

c.ii.  `text(Any function and its inverse intersect on)`

   `text(the line)\ \ y=x.`

`text(Solve:)\ \ 3-2x^3` `= xqquadtext(for)\ x,`
`x` `= 1`

 

`:.\ text{Intersection at (1, 1)}`
  

♦ Mean mark part (d)(i) 44%.
d.i.    `g^{prime}(x)` `= 0`
  `3x^2 + 4x + c` `= 0`
  `Delta` `= 0`
  `16-4(3c)` `= 0`
  `:. c` `= 4/3`

 

d.ii.   `text(Define)\ \ g(x) = x^3 + 2x^2 + 4/3x + k`

♦♦♦ Mean mark part (d)(ii) 14%.

  `text(Stationary point when)\ \ g^{prime}(x)=0`

`g^{prime}(x) = 3x^2+4x+4/3`

`text(Solve:)\ \ g^{prime}(x)=0\ \ text(for)\ x,`

`x = -2/3`

`text(Intersection of)\ g(x)\ text(and)\ g^(-1)(x)\ text(occurs on)\ \ y = x`

`text(Point of intersection is)\  (-2/3, -2/3)`

`text(Find)\ k:`

`g(-2/3)` `= -2/3\ text(for)\ k`
`:. k` ` = -10/27`

Probability, MET2 2011 VCAA 2*

In a chocolate factory the material for making each chocolate is sent to one of two machines, machine A or machine B.

The time, `X` seconds, taken to produce a chocolate by machine A, is normally distributed with mean 3 and standard deviation 0.8.

The time, `Y` seconds, taken to produce a chocolate by machine B, has the following probability density function
 

`f(y) = {{:(0,y < 0),(y/16,0 <= y <= 4),(0.25e^(−0.5(y-4)),y > 4):}`
 

  1. Find correct to four decimal places

    1. `text(Pr)(3 <= X <= 5)`   (1 mark)

    2. `text(Pr)(3 <= Y <= 5)`   (3 marks)

  2. Find the mean of `Y`, correct to three decimal places.   (3 marks)

  3. It can be shown that  `text(Pr)(Y <= 3) = 9/32`. A random sample of 10 chocolates produced by machine B is chosen. Find the probability, correct to four decimal places, that exactly 4 of these 10 chocolate took 3 or less seconds to produce.   (2 marks)

All of the chocolates produced by machine A and machine B are stored in a large bin. There is an equal number of chocolates from each machine in the bin.

It is found that if a chocolate, produced by either machine, takes longer than 3 seconds to produce then it can easily be identified by its darker colour.

  1. A chocolate is selected at random from the bin. It is found to have taken longer than 3 seconds to produce.
  2. Find, correct to four decimal places, the probability that it was produced by machine A.   (3 marks)

Show Answers Only

a.i.  `0.4938`

a.ii. `0.4155`

b.    `4.333`

c.    `0.1812`

d.    `0.4103`

Show Worked Solution

a.i.   `X ∼\ N(3,0.8^2)`

`text(Pr)(3 <= X <= 5) = 0.4938\ \ text{(4 d.p.)}`

 

a.ii.    `text(Pr)(3 <= Y <= 5)` `= text(Pr)(3 <= Y <= 4) + (4 < Y <= 5)`
    `= int_3^4 (y/16)dy + int_4^5(1/4 e^(−1/2(y-4)))dy`
    `= 0.4155\ \ text{(4 d.p.)}`

 

b.    `text(E)(Y)` `= int_0^4 y(y/16)dy + int_4^∞ 0.25ye^(−1/2(y-4))dy`
    `= 4.333\ \ text{(3 d.p.)}`

 

c.   `text(Solution 1)`

`text(Let)\ \ W = #\ text(chocolates from)\ B\ text(that take less)`

`text(than 3 seconds)`

`W ∼\ text(Bi)(10, 9/32)`

`text(Using CAS: binomPdf)(10, 9/32,4)`

`text(Pr)(W = 4) = 0.1812\ \ text{(4 d.p.)}`
 

`text(Solution 2)`

`text(Pr)(W = 4)`  `=((10),(4)) (9/32)^4 (23/32)^6` 
  `=0.1812`

♦♦♦ Mean mark part (e) 19%.
MARKER’S COMMENT: Students who used tree diagrams were the most successful.

 

d.   
`text(Pr)(A | L)` `= (text(Pr)(AL))/(text(Pr)(L))`
  `= (0.5 xx 0.5)/(0.5 xx 0.5 + 0.5 xx 23/32)`
  `= 0.4103\ \ text{(4 d.p.)}`

CORE, FUR2 SM-Bank 4

Damon runs a swim school.

The value of his pool pump is depreciated over time using flat rate depreciation.

Damon purchased the pool pump for $28 000 and its value in dollars after `n` years, `P_n`, is modelled by the recursion equation below:

`P_0 = 28\ 000,qquad P_(n + 1) = P_n - 3500`

  1. Write down calculations, using the recurrence relation, to find the pool pump's value after 3 years.   (1 mark)

  2. After how many years will the pump's depreciated value reduce to $7000?   (1 mark)

The reducing balance depreciation method can also be used by Damon.

Using this method, the value of the pump is depreciated by 15% each year.

A recursion relation that models its value in dollars after `n` years, `P_n`, is:

`P_0 = 28\ 000, qquad P_(n + 1) = 0.85P_n`

  1. After how many years does the reducing balance method first give the pump a higher valuation than the flat rate method in part (a)?   (2 marks)

Show Answers Only
  1. `$17\ 500`
  2. `6\ text(years)`
  3. `4\ text(years)`
Show Worked Solution
a.    `P_1` `= 28\ 000-3500 = 24\ 500`
  `P_2` `= 24\ 500-3500 = 21\ 000`
  `P_3` `= 21\ 000-3500 = 17\ 500`

  
`:.\ text(After 3 years, the pump’s value is $17 500.)`
  

b.   `text(Find)\ n\ text(such that:)`

`7000` `= 28\ 000-3500n`
`3500n` `= 21\ 000`
`n` `= (21\ 000)/3500`
  `= 6\ text(years)`

  
c.   `text(Using the reducing balance method)`

`P_1` `= 0.85 xx 28\ 000 = 23\ 800`
`P_2` `= 0.85 xx 23\ 800 = 20\ 230`
`P_3` `= 0.85 xx 20\ 230 = 17\ 195`
`P_4` `= 0.85 xx 17\ 195 = 14\ 615.75`

  
`text{Using the flat rate method (see part (a))}`

`P_4 = 17\ 500-3500 = 14\ 000`

`14\ 615.75 > 14\ 000`
  

`:.\ text(After 4 years, the reducing balance method)`

`text(first values the pump higher.)`

Calculus, MET2 2016 VCAA 4

  1. Express  `(2x + 1)/(x + 2)`  in the form  `a + b/(x + 2)`,  where `a` and `b` are non-zero integers.   (2 marks)

  2. Let  `f: R text(\){−2} -> R,\ f(x) = (2x + 1)/(x + 2)`.
    1. Find the rule and domain of `f^(-1)`, the inverse function of `f`.   (2 marks)

    2. Part of the graphs of `f` and  `y = x`  are shown in the diagram below.
       

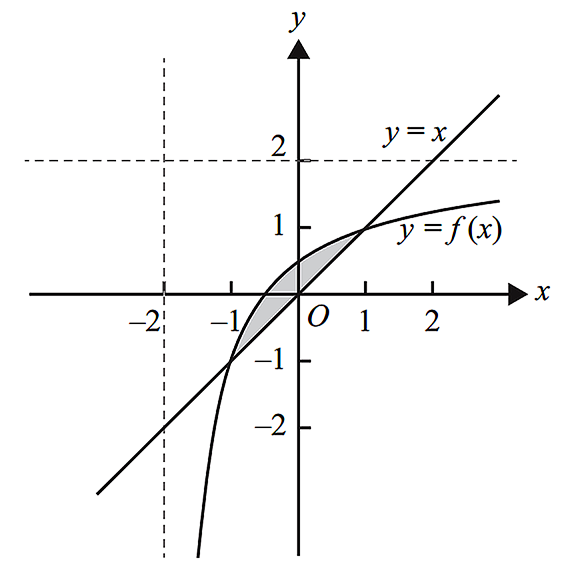
    3. Find the area of the shaded region.   (1 mark)

    4. Part of the graphs of `f` and `f^(-1)` are shown in the diagram below.
       

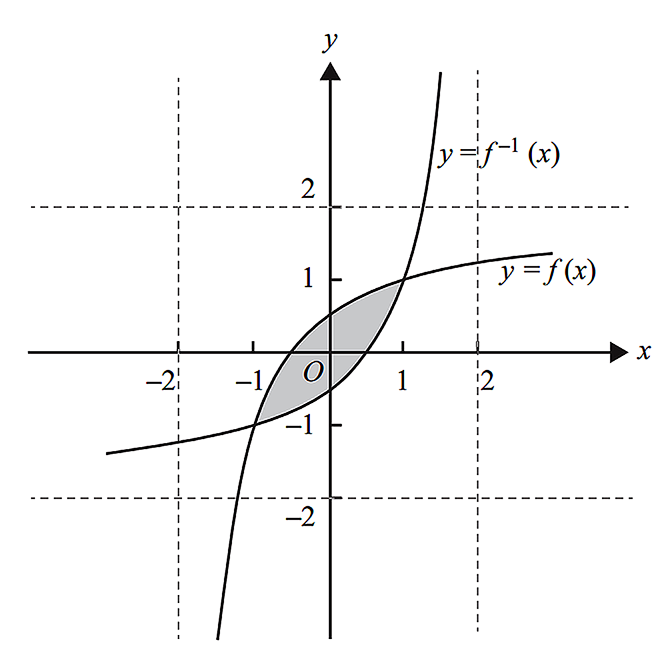
    5. Find the area of the shaded region.   (1 mark) 
  1. Part of the graph of `f` is shown in the diagram below.
     
       
     

     

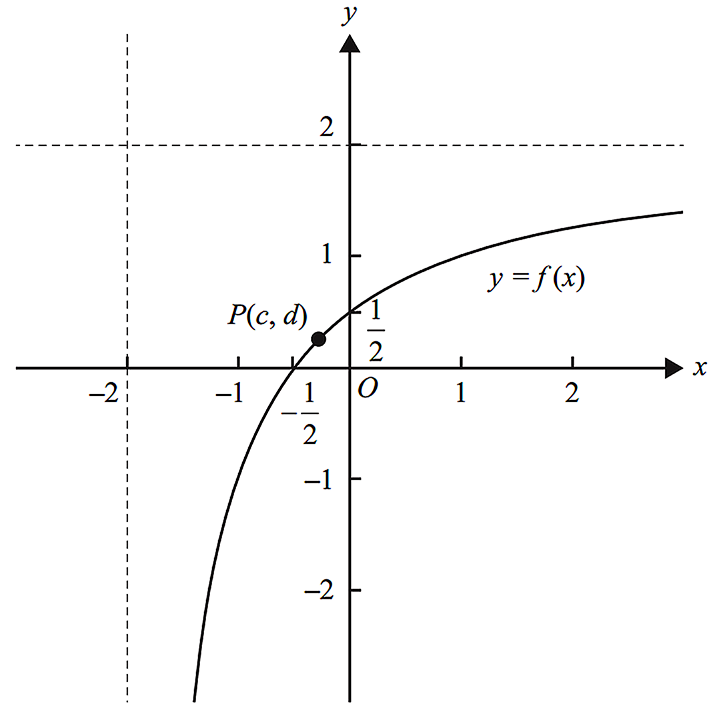
    The point `P(c, d)` is on the graph of `f`.

     

    Find the exact values of `c` and `d` such that the distance of this point to the origin is a minimum, and find this minimum distance.   (3 marks)

Let  `g: (−k, oo) -> R, g(x) = (kx + 1)/(x + k)`, where `k > 1`.

  1. Show that  `x_1 < x_2`  implies that  `g(x_1) < g(x_2),` where  `x_1 in (−k, oo) and x_2 in (−k, oo)`.   (2 marks)

  2. Let `X` be the point of intersection of the graphs of  `y = g (x) and y = −x`.
    1. Find the coordinates of `X` in terms of `k`.   (2 marks)

    2. Find the value of `k` for which the coordinates of `X` are  `(-1/2, 1/2)`.   (2 marks)

    3. Let  `Ztext{(− 1, − 1)}, Y(1, 1)`  and `X` be the vertices of the triangle `XYZ`. Let  `s(k)`  be the square of the area of triangle `XYZ`.
       

       

         
       

       

      Find the values of `k` such that  `s(k) >= 1`.   (2 marks)

  3. The graph of `g` and the line  `y = x`  enclose a region of the plane. The region is shown shaded in the diagram below.
     

     

     

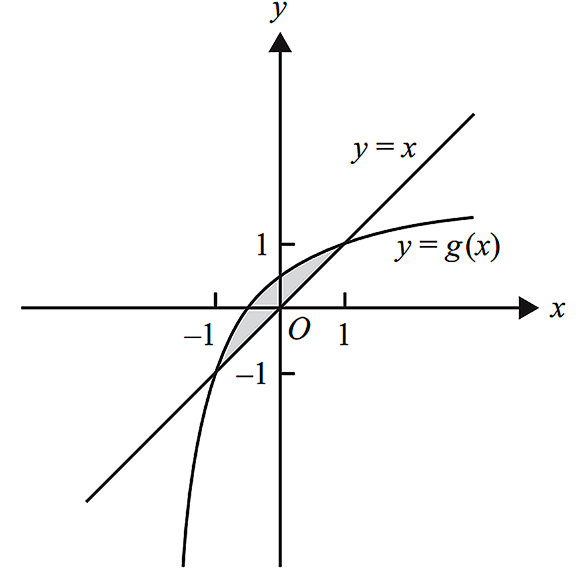
    Let  `A(k)`  be the rule of the function `A` that gives the area of this enclosed region. The domain of `A` is  `(1, oo)`.

    1. Give the rule for `A(k)`.   (2 marks)

    2. Show that  `0 < A(k) < 2`  for all  `k > 1`.   (2 marks)

Show Answers Only
  1. `2 + {(−3)}/(x + 2)`
  2.   i. `f^(-1) (x) = (-3)/(x-2)-2,\ \ x in R text(\){2}`
  3.  ii. `4-3 ln(3)\ text(units²)`
  4. iii. `8-6 log_e (3)\ text(units²)`
  5. `c = sqrt 3-2, \ d = 2-sqrt 3`
  6. `text(min distance) = (2 sqrt 2-sqrt 6)`
  7. `text(Proof)\ \ text{(See Worked Solutions)}`
  8.   i. `X (−k + sqrt (k^2-1), k-sqrt (k^2-1))`
  9.  ii. `k = 5/4`
  10. iii. `k in (1, 5/4]`
  11.  i. `A(k) = (k^2-1) log_e ((k-1)/(k + 1)) + 2k`
  12. ii. `text(Proof)\ \ text{(See Worked Solutions)}`
Show Worked Solution

a.   `text(Solution 1)`

`(2x + 1)/(x + 2)` `= 2-3/(x + 2)`
  `= 2 + {(-3)}/(x + 2) qquad [text(CAS: prop Frac) ((2x + 1)/(x + 2))]`

 

`text(Solution 2)`

`(2x + 1)/(x + 2)` `=(2(x+2)-3)/(x+2)`
  `=2+ (-3)/(x+2)`

 

b.i.  `text(Let)\ \ y = f(x)`

`text(For Inverse: swap)\ \ x ↔ y`

`x` `=2-3/(y + 2)`
`(x-2)(y+2)` `=-3`
`y` `=(-3)/(x-2)-2`

 

`text(Range of)\ f(x):\ \ y in R text(\){2}`

`:. f^(-1) (x) = (-3)/(x-2)-2, \ x in R text(\){2}`

 

b.ii.   `text(Find intersection points:)`

`f(x)` `= x`
`(2x+1)/(x+2)` `=x`
`2x+1` `=x^2+2x`
`:. x` `= +- 1`
`:.\ text(Area)` `= int_(-1)^1 (f(x)-x)\ dx`
  `=int_(-1)^1 (2-3/(x + 2)-x)\ dx`
  `= 4-3 ln(3)\ text(u²)`

 

b.iii.    `text(Area)` `= int_(-1)^1 (f(x)-f^(-1) (x)) dx`
    `=2 xx (4-3 ln(3))\ \ \ text{(twice the area in (b)(ii))}`
    `= 8-6 log_e (3)\ text(u²)`
♦♦♦ Mean mark part (c) 25%.

 

c.   
  `text(Let)\ \ z` `= OP, qquad P(c, -3/(c + 2) + 2)`
  `z` `= sqrt (c^2 + (2-3/(c + 2))^2), \ c > -2`

`text(Stationary point when:)`

`(dz)/(dc) = 0, c > -2`

`:.\ c = sqrt 3-2 overset and (->) d = 2-sqrt 3`

`:. text(Minimum distance) = (2 sqrt 2-sqrt 6)`

 

d.   `text(Given:)\ \ -k < x_1 < x_2`

♦♦♦ Mean mark part (d) 8%.

`text(Must prove:)\ \ g(x_2)-g(x_1) > 0`

`text(LHS:)`

`g(x_2)-g(x_1)`

`= (kx_2 +1)/(x_2+k)-(kx_1 +1)/(x_1+k)`

`=((kx_2 +1)(x_1+k)-(kx_1 +1)(x_2+k))/((x_2+k)(x_1+k))`

`=(k^2(x_2-x_1)-(x_2-x_1))/((x_2+k)(x_1+k))`

`=((k^2-1)(x_2-x_1))/((x_2+k)(x_1+k))`

 

`x_2-x_1 >0,\ and \ k^2-1>0`

`text(S)text(ince)\ \ x_2>x_1> -k,`

`=> -x_2<-x_1<k`

`=>k+x_1 >0, \ and \ k+x_2>0`

 

`:.g(x_2)-g(x_1) >0`

`:. g(x_2) > g(x_1)`

 

♦♦ Mean mark part (e)(i) 32%.
e.i.    `g(x)` `= -x`
  `(kx +1)/(x+k)` `=-x`
  `kx+1` `=-x^2-xk`
  `x^2+2k+1` `=0`
  `:. x` `=(-2k +- sqrt(4k^2-4))/2`
    `= sqrt (k^2-1)-k\ \ text(for)\ \ x > -k`

 

`:. X (-k + sqrt(k^2-1),\ \ k-sqrt(k^2-1))`

 

e.ii.   `text(Equate)\ \ x text(-coordinates:)`

♦ Mean mark part (e)(ii) 44%.
`-k + sqrt(k^2-1)` `= -1/2`
`sqrt(k^2-1)` `=k-1/2`
`k^2-1` `=k^2-k+1/4`
`:. k` `= 5/4`

 

e.iii.   `s(k)` `= (1/2 xx YZ xx XO)^2`
    `= 1/4 xx (YZ)^2 xx (XO)^2`

 

`ZO = sqrt(1^2+1^2) = sqrt2`

♦♦♦ Mean mark (e)(iii) 6%.

`YZ=2 xx ZO = 2sqrt2`

`(YZ)^2 = 8`

`(XO)^2` `=(-k + sqrt(k^2-1))^2-(k-sqrt (k^2-1))^2`
  `=2(-k + sqrt(k^2-1))^2`
   

 `text(Solve)\ \ s(k) >= 1\ \ text(for)\ \ k >= 1,`

`1/4 xx 8 xx 2(-k + sqrt(k^2-1))^2` `>=1`
`(-k + sqrt(k^2-1))^2` `>=1/4`
`k-sqrt(k^2-1)` `>=1/2`
`k-1/2` `>= sqrt(k^2-1)`
`k^2-k+1/4` `>=k^2-1`
`:.k` `<= 5/4`

`:.  1<k<= 5/4`

 

♦♦ Mean mark (f)(i) 28%.
f.i.    `A(k)` `= int_(-1)^1 (g(x)-x)\ dx,\ \ k > 1`
    `= int_(-1)^1 ((kx+1)/(x+k) -x)\ dx`
    `= int_(-1)^1 (k+ (1-k^2)/(x+k) -x)`
    `=[kx + (1-k^2) log_e(x+k)-x^2/2]_(-1)^1`
    `=(k+(1-k^2)log_e(1+k)-1/2)-(-k+(1-k^2)log_e(k-1)-1/2)`
    `=2k+(1-k^2)log_e ((1+k)/(k-1))`
    `= (k^2-1) log_e ((k-1)/(k + 1)) + 2k`

 

♦♦♦ Mean mark part (f)(ii) 4%.
f.ii.  
  `0` `< A(k) < text(Area of)\ Delta ABC`
  `0` `< A(k) < 1/2 xx AC xx BO`
  `0` `< A(k) < 1/2 sqrt(2^2 + 2^2) xx (sqrt(1^2 + 1^2))`
  `0` `< A(k) < 1/2 xx 2 sqrt 2 xx sqrt 2`
  `:. 0` `< A(k) < 2`

Probability, MET2 2016 VCAA 3*

A school has a class set of 22 new laptops kept in a recharging trolley. Provided each laptop is correctly plugged into the trolley after use, its battery recharges.

On a particular day, a class of 22 students uses the laptops. All laptop batteries are fully charged at the start of the lesson. Each student uses and returns exactly one laptop. The probability that a student does not correctly plug their laptop into the trolley at the end of the lesson is 10%. The correctness of any student’s plugging-in is independent of any other student’s correctness.

  1. Determine the probability that at least one of the laptops is not correctly plugged into the trolley at the end of the lesson. Give your answer correct to four decimal places.   (2 marks)

  2. A teacher observes that at least one of the returned laptops is not correctly plugged into the trolley.
  3. Given this, find the probability that fewer than five laptops are not correctly plugged in. Give your answer correct to four decimal places.   (2 marks)

The time for which a laptop will work without recharging (the battery life) is normally distributed, with a mean of three hours and 10 minutes and standard deviation of six minutes. Suppose that the laptops remain out of the recharging trolley for three hours.

  1. For any one laptop, find the probability that it will stop working by the end of these three hours. Give your answer correct to four decimal places.   (2 marks)

A supplier of laptops decides to take a sample of 100 new laptops from a number of different schools. For samples of size 100 from the population of laptops with a mean battery life of three hours and 10 minutes and standard deviation of six minutes, `hat P` is the random variable of the distribution of sample proportions of laptops with a battery life of less than three hours.

  1. Find the probability that `text(Pr) (hat P >= 0.06 | hat P >= 0.05)`. Give your answer correct to three decimal places. Do not use a normal approximation.   (3 marks)

It is known that when laptops have been used regularly in a school for six months, their battery life is still normally distributed but the mean battery life drops to three hours. It is also known that only 12% of such laptops work for more than three hours and 10 minutes.

  1. Find the standard deviation for the normal distribution that applies to the battery life of laptops that have been used regularly in a school for six months, correct to four decimal places.   (2 marks)

The laptop supplier collects a sample of 100 laptops that have been used for six months from a number of different schools and tests their battery life. The laptop supplier wishes to estimate the proportion of such laptops with a battery life of less than three hours.

  1. Suppose the supplier tests the battery life of the laptops one at a time.
  2. Find the probability that the first laptop found to have a battery life of less than three hours is the third one.   (1 mark)

The laptop supplier finds that, in a particular sample of 100 laptops, six of them have a battery life of less than three hours.

  1. Determine the 95% confidence interval for the supplier’s estimate of the proportion of interest. Give values correct to two decimal places.   (1 mark)

  2. The supplier also provides laptops to businesses. The probability density function for battery life, `x` (in minutes), of a laptop after six months of use in a business is
     

     

    `qquad qquad f(x) = {(((210-x)e^((x-210)/20))/400, 0 <= x <= 210), (0, text{elsewhere}):}`
     

  3. Find the mean battery life, in minutes, of a laptop with six months of business use, correct to two decimal places.   (1 mark)

Show Answers Only

  1. `0.9015`
  2. `0.9311`
  3. `0.0478`
  4. `0.658`
  5. `8.5107`
  6. `1/8`
  7. `p in (0.01, 0.11)`
  8. `170.01\ text(min)`

Show Worked Solution

a.   `text(Solution 1)`

`text(Let)\ \ X = text(number not correctly plugged),`

`X ~ text(Bi) (22, .1)`

`text(Pr) (X >= 1) = 0.9015\ \ [text(CAS: binomCdf)\ (22, .1, 1, 22)]`

 

`text(Solution 2)`

`text(Pr) (X>=1)` `=1-text(Pr) (X=0)`
  `=1-0.9^22`
  `=0.9015\ \ text{(4 d.p.)}`

 

 b.   `text(Pr) (X < 5 | X >= 1)`

MARKER’S COMMENT: Early rounding was a common mistake, producing 0.9312.

`= (text{Pr} (1 <= X <= 4))/(text{Pr} (X >= 1))`

`= (0.83938…)/(0.9015…)\ \ [text(CAS: binomCdf)\ (22, .1, 1,4)]`

`= 0.9311\ \ text{(4 d.p.)}`

 

c.   `text(Let)\ \ Y = text(battery life in minutes)`

MARKER’S COMMENT: Some working must be shown for full marks in questions worth more than 1 mark.

`Y ~ N (190, 6^2)`

`text(Pr) (Y <= 180)= 0.0478\ \ text{(4 d.p.)}`

`[text(CAS: normCdf)\ (−oo, 180, 190,6)]`

 

d.   `text(Let)\ \ W = text(number with battery life less than 3 hours)`

♦ Mean mark part (d) 33%.

`W ~ Bi (100, .04779…)`

`text(Pr) (hat P >= .06 | hat P >= .05)` `= text(Pr) (X_2 >= 6 | X_2 >= 5)`
  `= (text{Pr} (X_2 >= 6))/(text{Pr} (X_2 >= 5))`
  `= (0.3443…)/(0.5234…)`
  `= 0.658\ \ text{(3 d.p.)}`

 

e.   `text(Let)\ \ B = text(battery life), B ~ N (180, sigma^2)`

`text(Pr) (B > 190)` `= .12`
`text(Pr) (Z < a)` `= 0.88`
`a` `dot = 1.17499…\ \ [text(CAS: invNorm)\ (0.88, 0, 1)]`
`-> 1.17499` `= (190-180)/sigma\ \ [text(Using)\ Z = (X-u)/sigma]`
`:. sigma` `dot = 8.5107`

 

f.    `text(Pr) (MML)` `= 1/2 xx 1/2 xx 1/2`
    `= 1/8`

 

g.   `text(95% confidence int:) qquad quad [(text(CAS:) qquad qquad 1-text(Prop)\ \ z\ \ text(Interval)), (x = 6), (n = 100)]`

`p in (0.01, 0.11)`

 

h.    `mu` `= int_0^210 (x* f(x)) dx`
  `:. mu` `dot = 170.01\ text(min)`

Calculus, MET2 2016 VCAA 2

Consider the function  `f(x) = -1/3 (x + 2) (x-1)^2.`

  1.  i. Given that  `g^{′}(x) = f (x) and g (0) = 1`,
  2.      show that  `g(x) = -x^4/12 + x^2/2-(2x)/3 + 1`.   (1 mark)

  3. ii. Find the values of `x` for which the graph of  `y = g(x)`  has a stationary point.   (1 mark)

The diagram below shows part of the graph of  `y = g(x)`, the tangent to the graph at  `x = 2`  and a straight line drawn perpendicular to the tangent to the graph at  `x = 2`. The equation of the tangent at the point `A` with coordinates  `(2, g(2))`  is  `y = 3-(4x)/3`.

The tangent cuts the `y`-axis at `B`. The line perpendicular to the tangent cuts the `y`-axis at `C`.
 


 

  1.   i. Find the coordinates of `B`.   (1 mark)

  2.  ii. Find the equation of the line that passes through `A` and `C` and, hence, find the coordinates of `C`.   (2 marks)

  3. iii. Find the area of triangle `ABC`.   (2 marks)

  4. The tangent at `D` is parallel to the tangent at `A`. It intersects the line passing through `A` and `C` at `E`.

     


     
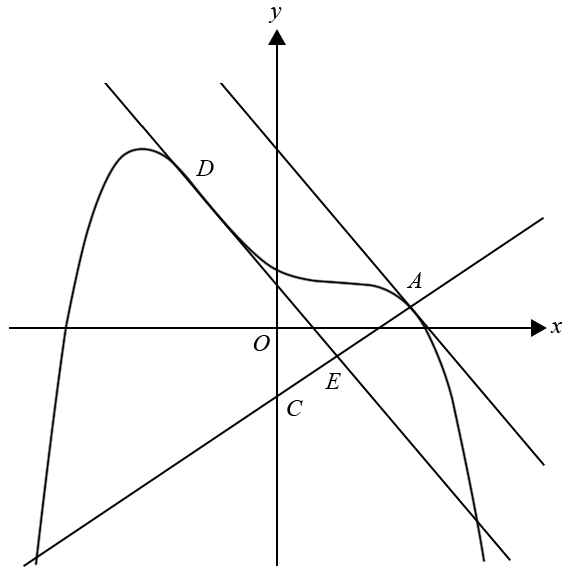
     i. Find the coordinates of `D`.   (2 marks)

  5. ii. Find the length of `AE`.   (3 marks)

Show Answers Only
  1.  i. `text(Proof)\ \ text{(See worked solutions)}`
  2. ii. `x = -2, 1`
  3.   i. `(0, 3)`
  4. ii. `y = 3/4 x-7/6`
  5.      `(0, -7/6)`
  6. iii. `25/6\ text(u²)`
  7. `(-1, 25/12)`
  8. `27/20\ text(u)`
Show Worked Solution
a.i.    `g(x)` `= int f(x)\ dx`
    `=-1/3 int (x + 2) (x-1)^2\ dx`
    `=-1/3int(x^3-3x+2)\ dx`
  `:.g(x)` `= -x^4/12 + x^2/2-(2x)/3 + c`

 
`text(S)text(ince)\ \ g(0) = 1,`

`1` `= 0 + 0-0 + c`
`:. c` `= 1`

  
`:. g(x) = -x^4/12 + x^2/2-(2x)/3 + 1\ \ …\ text(as required)`
 

a.ii.   `text(Stationary point when:)`

`g^{′}(x) = f(x) = 0`

`-1/3(x + 2) (x-1)^2=0`

`:. x = -2, 1`
 

b.i.   

`B\ text(is the)\ y text(-intercept of)\ \ y = 3-4/3 x`

`:. B (0, 3)`
 

b.ii.   `m_text(norm) = 3/4, \ text(passes through)\ \ A(2, 1/3)`

   `text(Equation of normal:)`

`y-1/3` `=3/4(x-2)`
`y` `=3/4 x-7/6`
   

`:. C (0, -7/6)`
 

b.iii.   `text(Area)` `= 1/2 xx text(base) xx text(height)`
    `= 1/2 xx (3 + 7/6) xx 2`
    `= 25/6\ text(u²)`

 

♦ Mean mark part (c)(i) 43%.
MARKER’S COMMENT: Many students gave an incorrect `y`-value here. Be careful!
c.i.    `text(Solve)\ \ \ g^{′}(x)` `= -4/3\ \ text(for)\ \ x < 0`
  `=> x` `= -1`
  `g(-1)` `=-1/12+1/2+2/3+1`
    `=25/12`

  
`:. D (−1, 25/12)`
 

c.ii.   `text(T) text(angent line at)\ \ D:`

`y-25/12` `=-4/3(x+1)`
`y` `=-4/3x + 3/4`

 
`DE\ \ text(intersects)\ \ AE\ text(at)\ E:`

♦♦ Mean mark 32%.
`-4/3 x + 3/4` `= 3/4 x-7/6`
`25/12 x` `= 23/12`
`x` `=23/25`

 
`:. E (23/25, -143/300)`
 

`:. AE` `= sqrt((2-23/25)^2 + (1/3-(-143/300))^2)`
  `= 27/20\ text(units)`

Calculus, MET2 2016 VCAA 1

Let  `f: [0, 8 pi] -> R, \ f(x) = 2 cos (x/2) + pi`.

  1. Find the period and range of `f`.   (2 marks)

  2. State the rule for the derivative function `f^{′}`.   (1 mark)

  3. Find the equation of the tangent to the graph of `f` at  `x = pi`.   (1 mark)

  4. Find the equations of the tangents to the graph of  `f: [0, 8 pi] -> R,\ \ f(x) = 2 cos (x/2) + pi`  that have a gradient of 1.   (2 marks)

  5. The rule of  `f^{′}` can be obtained from the rule of `f` under a transformation `T`, such that
      
    `qquad T: R^2 -> R^2,\ T([(x), (y)]) = [(1, 0), (0, a)] [(x), (y)] + [(−pi), (b)]`
     

     

    Find the value of `a` and the value of `b`.   (3 marks)

  6. Find the values of  `x, \ 0 <= x <= 8 pi`, such that  `f(x) = 2 f^{′} (x) + pi`.   (2 marks)

Show Answers Only
  1. `text(Period:)\ 4 pi; qquad text(Range:)\ [pi-2, pi + 2]`
  2. `f^{′} (x) =-sin (x/2)`
  3. `y =-x + 2 pi`
  4. `y = x-2 pi and y = x-6 pi`
  5. `a = 1/2 and b =-pi/2`
  6. `x = (3 pi)/2, (7 pi)/2, (11 pi)/2, (15 pi)/2`
Show Worked Solution

a.   `text(Period)= (2pi)/n = (2 pi)/(1/2) = 4pi`

MARKER’S COMMENT: Including round brackets rather than square ones was a common mistake.

`text(Range:)\ [pi-2, pi + 2]`
  

b.   `f^{′} (x) = text(−sin) (x/2)`
 

c.   `[text(CAS: tangentLine)\ (f(x), x, pi)]`

`y = -x + 2 pi`
 

d.   `text(Solve)\ \ f^{′} (x) = 1\ \ text(for)\ x in [0, 8 pi]`

♦ Mean mark part (d) 50%.

`-> x = 3 pi or 7 pi`

`:. y = x-2 pi and y = x-6 pi\ \ [text(CAS)]`

 

e.   `text(Using the transition matrix,)`

♦♦ Mean mark part (e) 27%.
`x_T` `=x-pi`
`x` `=x_T+pi`
`y_T` `=ay+b`
`y` `=(y_T-b)/a`
   

`f(x)= cos (x/2) + pi/2\ \ ->\ \ f{′}(x) = -sin(x/2)`

`(y_T-b)/a` `=2cos((x_T+pi)/2)+pi`
`y_T` `=2a cos((x_T+pi)/2)+a pi +b`
  `=-2a sin(x_T/2)+a pi + bqquad [text(Complementary Angles)]`
   
`-2a` `=-1`
`:. a` `=1/2`
`1/2 pi +b` `=0`
`:.b` `=-pi/2`

 

f.   `text(Solve)\ \ f(x) = 2 f^{′} (x) + pi\ \ text(for)\ \ x in [0, 8 pi]`

♦ Mean mark part (f) 50%.
`2 cos (x/2) + pi` `= -2 sin(x/2)+pi`
`tan(x/2)` `=-1`
`x/2` `=(3pi)/4, (7pi)/4, (11pi)/4, (15pi)/4`
`:.x` `= (3 pi)/2, (7 pi)/2, (11 pi)/2, (15 pi)/2`

Calculus, MET2 2010 VCAA 17 MC

The function `f` is differentiable for all  `x in R`  and satisfies the following conditions.

  • `f prime (x) < 0\ \ text(where)\ \ x < 2`
  • `f prime (x) = 0\ \ text(where)\ \ x = 2`
  • `f prime (x) = 0\ \ text(where)\ \ x = 4`
  • `f prime (x) > 0\ \ text(where)\ \ 2 < x < 4`
  • `f prime (x) > 0\ \ text(where)\ \ x > 4`

Which one of the following is true?

  1.  The graph of `f` has a local maximum point where `x = 4.`
  2. The graph of `f` has a stationary point of inflection where `x = 4.`
  3. The graph of `f` has a local maximum point where `x = 2.`
  4. The graph of `f` has a local minimum point where `x = 4.`
  5. The graph of `f` has a stationary point of inflection where `x = 2.`
Show Answers Only

`B`

Show Worked Solution

`text(A table summary of the gradients is:)`

 

`:.\ text(Point of Inflection at)\ \ x = 4`

`=>   B`

Probability, MET2 2010 VCAA 13 MC

The continuous random variable `X` has a normal distribution with mean 20 and standard deviation 6. The continuous random variable `Z` has the standard normal distribution.

The probability that `Z` is between – 2 and 1 is equal to

  1. `text(Pr) (18 < X < 21)`
  2. `text(Pr) (14 < X < 32)`
  3. `text(Pr) (14 < X < 26)`
  4. `text(Pr) (8 < X < 32)`
  5. `text(Pr) (X > 14) + text(Pr) (X < 26)`
Show Answers Only

`B`

Show Worked Solution

`text(When)\ \ Z=-2,`

`X=mu – 2σ = 20-2xx6 = 8`

`text(When)\ \ Z=1,`

`X=mu + σ = 20+6 = 26`

`text(Due to symmetry,)`

`text(Pr) (-2<Z<1)` `= text(Pr) (8<X<26)`
  `= text(Pr) (14<X<32)`

`=>   B`

Probability, MET2 2010 VCAA 11 MC

The continuous random variable `X` has a probability density function given  by
 

`f(x) = {(cos(2x), if (3 pi)/4 < x < (5 pi)/4), (qquad qquad quad 0,\ \ \ text(elsewhere)):}`
 

The value of `a` such that `text(Pr) (X < a) = 0.25`  is closest to

  1. `2.25`
  2. `2.75`
  3. `2.88`
  4. `3.06`
  5. `3.41`
Show Answers Only

`C`

Show Worked Solution

`text(Solve)\ \ int_((3 pi)/4)^a cos (2x)\ dx = 1/4\ \ text(for)\ \ a in ((3 pi)/4, (5 pi)/4)`

`:. a` `= (11 pi)/12\ \ \ text([by CAS.])`
  `~~ 2.88`

 
`=>   C`

Algebra, MET2 2010 VCAA 9 MC

The function  `f:\ (–oo, a] -> R`  with rule  `f(x) = x^3 - 3x^2 + 3`  will have an inverse function provided

  1. `a <= 0`
  2. `a >= 2`
  3. `a >= 0`
  4. `a <= 2`
  5. `a <= 1`
Show Answers Only

`A`

Show Worked Solution
`f(x)` `= x^3-3x^2 + 3`
`f′(x)` `=3x^2-6x`
  `=3x(x-2)`

 

`text(Stationary points at)\ \ x=0 and 2.`

`text{Local max at (0,3) and local min at (2,-1).}`

`text(Sketch the graph:)`

`text(Inverse exists if)\ \ f(x)\ \ text(is)\ \ 1-1.`

`:. x <= 0`

`=>   A`

Calculus, MET2 2010 VCAA 2 MC

For  `f(x) = x^3 + 2x`, the average  rate of change with respect to `x` for the interval  `[1, 5]`  is

A.   `18`

B.   `20.5`

C.   `24`

D.   `32.5`

E.   `33`

Show Answers Only

`E`

Show Worked Solution
`text(Average ROC)` `= (f(5) – f(1))/(5 – 1)`
  `=(135-3)/4`
  `= 33`

`=>   E`

Probability, MET2 2016 VCAA 18 MC

The continuous random variable, `X`, has a probability density function given by
 

`qquad f(x) = {(1/4 cos (x/2), 3 pi <= x <= 5 pi), (0, text{elsewhere}):}`
 

The value of `a` such that  `text(Pr) (X < a) = (sqrt 3 + 2)/4`  is

  1. `(19 pi)/6`
  2. `(14 pi)/3`
  3. `(10 pi)/3`
  4. `(29 pi)/6`
  5. `(17 pi)/3`
Show Answers Only

`B`

Show Worked Solution
`int_(3 pi)^a f(x)\ dx` `= (sqrt 3 + 2)/4`
`[1/2 sin (x/2)]_(3pi)^a` `= (sqrt 3 + 2)/4`
`1/2 sin (a/2) +1/2` `= (sqrt 3 + 2)/4`
`sin (a/2)` `=sqrt3/2`
`a/2` `=pi/3, (2pi)/3, (4pi)/3, (5pi)/3, (7pi)/3, …`
`:. a` `= (14 pi)/3\ \ text(for)\ a in (3 pi, 5 pi)`

 
`=>   B`

Probability, MET2 2016 VCAA 17 MC

Inside a container there are one million coloured building blocks. It is known that 20% of the blocks are red.

A sample of 16 blocks is taken from the container. For samples of 16 blocks, `hat P` is the random variable of the distribution of sample proportions of red blocks. (Do not use a normal approximation.)

`text(Pr) (hat P >= 3/16)` is closest to

A.  `0.6482`

B.  `0.8593`

C.  `0.7543`

D.  `0.6542`

E.  `0.3211`

Show Answers Only

`A`

Show Worked Solution

`text(Let)\ \ X = text(Number of red blocks),`

`X ~\ text(Bi) (16, 0.2)`

`text(Pr) (hat P >= 3/16)`

`= text(Pr) (X >= 3) qquad [text(binomCdf) (16, .2, 3, 16)]`

`= 0.6482`

`=>   A`

Calculus, MET2 2016 VCAA 13 MC

Consider the graphs of the functions `f` and `g` shown below.

The area of the shaded region could be represented by

A.   `int_a^d (f(x) - g(x))\ dx`

B.   `int_0^d (f(x) - g(x))\ dx`

C.   `int_0^b (f(x) - g(x))\ dx + int_b^c (f(x) - g(x))\ dx`

D.   `int_0^a f(x)\ dx + int_a^c (f(x) - g(x))\ dx + int_b^d f(x)\ dx`

E.   `int_0^d f(x)\ dx - int_a^c g(x)\ dx`

Show Answers Only

`E`

Show Worked Solution

`text(Shaded Area:)`

`text(Area under)\ f(x)\ text(between)\ [0, d]\ text(less)`

`text(Area under)\ g(x)\ text(between)\ [a, c]`

`=>   E`

Graphs, MET2 2016 VCAA 12 MC

The graph of a function  `f` is obtained from the graph of the function `g` with rule  `g(x) = sqrt (2x - 5)`  by a reflection in the `x`-axis followed by a dilation from the `y`-axis by a factor of  `1/2`.

Which one of the following is the rule for the function  `f`?

  1. `f(x) = sqrt (5 - 4x)`
  2. `f(x) = - sqrt (x - 5)`
  3. `f(x) = sqrt (x + 5)`
  4. `f(x) = −sqrt (4x - 5)`
  5. `f(x) = −sqrt (4x - 10)`
Show Answers Only

`D`

Show Worked Solution

`text(Let)\ \ y=sqrt(2x-5)`

`text(1st transformation:)`

`y = – sqrt(2x-5)`
 

`text(2nd transformation:)`

`y` `=-sqrt(2(2x)-5)`
  `=- sqrt(4x-5)`
`:. f(x)` `= −sqrt(4x – 5)`

 
`=>   D`

Calculus, MET2 2016 VCAA 10 MC

For the curve  `y = x^2 - 5`, the tangent to the curve will be parallel to the line connecting the positive x-intercept and the y-intercept when `x` is equal to

A.   `sqrt 5`

B.   `5`

C.   `−5`

D.   `sqrt 5/2`

E.   `1/sqrt 5`

Show Answers Only

`D`

Show Worked Solution

`text{Intercepts: (0, −5) and}\ (sqrt 5, 0)`

`text(Gradient between intercepts:)`

`m = (0 – (−5))/(sqrt 5 – 0) = 5/sqrt 5`

`text(Solve:)`

`f prime (x)` `= 5/sqrt 5`
`2x` `= 5/sqrt 5`
`:. x` `=5/(2sqrt5) xx sqrt5/sqrt5`
  `= sqrt 5/2`

 
`=>   D`

Graphs, MET2 2016 VCAA 6 MC

Consider the graph of the function defined by  `f: [0, 2 pi] -> R,\ f(x) = sin (2x).`

The square of the length of the line segment joining the points on the graph for which  `x = pi/4 and x = (3 pi)/4` is

  1. `(pi^2 + 16)/4`
  2. `pi + 4`
  3. `4`
  4. `(3 pi^2 + 16 pi)/4`
  5. `(10 pi^2)/16`
Show Answers Only

`A`

Show Worked Solution

`text(When)\ \ x=pi/4,\ \ f(x) = sin(pi/2)=1`

`text(When)\ \ x=(3pi)/4,\ \ f(x) = sin((3pi)/2)=-1`

`text(Let)\ \ z` `= text(distance between)\ (pi/4, 1) and ((3pi)/4, −1)`
`z^2` `= ((3pi)/4 – pi/4)^2 + (−1 −1)^2`
   `=pi^2/4 + 4`
  `= (pi^2 + 16)/4`

`=>   A`

Calculus, MET2 2011 VCAA 20 MC

A part of the graph of  `g: R -> R, g(x) = x^2 - 4`  is shown below.

met2-2011-vcaa-20-mc

The area of the region marked `A` is the same area of the region marked `B`.

The exact value of `a` is

A.   `0`

B.   `6`

C.   `sqrt6`

D.   `12`

E.   `2sqrt3` 

Show Answers Only

`=> E`

Show Worked Solution

`text(S)text(ince Area)\ A = text(Area)\ B,`

`int_0^a (x^2-4)\ dx` `=0`
`[x^3/3 – 4x]_0^a` `=0`
`a^3/3 – 4a` `=0`
`a^2` `=12`
`:.a` `=2sqrt3,\ \ text(for)\ a > 0`

`=> E`

Algebra, MET2 2011 VCAA 18 MC

The equation  `x^3 - 9x^2 + 15x + w = 0`  has only one solution for `x` when

A.   `−7 < w < 25`

B.   `w <= −7`

C.   `w >=25`

D.   `w < −7` or `w > 25`

E.   `w > 1`

Show Answers Only

`=> D`

Show Worked Solution
`y` `=x^3 – 9x^2 + 15x + w`
`y′` `=3x^2 – 18x + 15`
  `=3(x-5)(x-1)`

 

`text(Stationary points at)\ \ x=5 and 1.`

`text{Sketch the graph}\ \ (w=0),`

met2-2011-vcaa-18-mc-answer
 

`text(By inspection, one solution occurs when)`

`w > 25\ \ text{(shift curve up > 25), or}`

`w < −7\ \ text{(shift curve down > 7)`

`=> D`

Graphs, MET2 2011 VCAA 15 MC

met2-2011-vcaa-15-mc 
 

The graph shown could have equation

  1. `y = 2cos(x + pi/6) + 1`
  2. `y = 2cos4(x - pi/6) + 1`
  3. `y = 4sin2(x - pi/12) - 1`
  4. `y = 3cos(2x + pi/6) - 1`
  5. `y = 2sin(4x + (2pi)/3) - 1`
Show Answers Only

`=> B`

Show Worked Solution

`text{Amplitude = 2  (range from – 1 to 3)}`

`text(Median) = 1`

`:.\ text(Solution is)\ A\ text(or)\ B.`

`text(From graph:)`

`text(Period) = (2pi)/3 – pi/6 = pi/2`

`text(Consider option)\ B,`

`text(Period)= (2pi)/n= (2pi)/4 = pi/2`

`=> B`

Probability, MET2 2011 VCAA 12 MC

The continuous random variable `X` has a normal distribution with mean 30 and standard deviation 5. For a given number `a, text(Pr)(X > a) = 0.20`.

Correct to two decimal places, `a` is equal to

  1. `23.59`
  2. `24.00`
  3. `25.79`
  4. `34.21`
  5. `36.41`
Show Answers Only

`=> D`

Show Worked Solution

met2-2011-vcaa-12-mc-answer1

`X ∼\ N(30,5^2)`

`text(Pr)(X < a)` `= 0.8qquad[text(CAS: inv Norm) (.8,30,5)]`
`:. a` `= 34.21`

`=> D`

Graphs, MET2 2011 VCAA 8 MC

Consider the function  `f: R -> R, \ f(x) = x(x - 4)`  and the function

`g: [3/2,5) -> R, \ g(x) = x + 3`.

If the function  `h = f + g`, then the domain of the inverse function of `h` is

  1. `[0,13)`
  2. `[−3/4,10]`
  3. `(−3/4,15/4]`
  4. `[3/4,13)`
  5. `[3/2,13)` 
Show Answers Only

`=> D`

Show Worked Solution
`h(x)` `= x^2 – 3x + 3, \ x ∈[3/2,5)`
`h′(x)` `=2x-3`

 
`:.\ text(Minimum at)\ \ (3/2, 3/4)`

`h(5)=5^2 -3 xx 5 +3=13`

 

`text(Sketch the graph:)` 

met1-2011-vcaa-8-mc-answer

`text(Domain) (h^(−1)(x))` `= text(Range)\ (h)`
  `= [3/4,13)`

`=> D`

Calculus, MET2 2011 VCAA 4 MC

The derivative of  `log_e(2f(x))`  with respect to `x` is

  1. `(f′(x))/(f(x))`
  2. `2(f′(x))/(f(x))`
  3. `(f′(x))/(2f(x))`
  4. `log_e(2f′(x))`
  5. `2log_e(2f′(x))`
Show Answers Only

`A`

Show Worked Solution

`text(Chain Rule:)`

`text(If)\ \ h(x)` `= f(g(x))`
`h′(x)` `= f′(g(x)) xx g′(x)`
`d/(dx)(log_e(2f(x)))` `= 1/(2f(x)) xx 2f′(x)`
  `= (f′(x))/(f(x))`

`=> A`

Algebra, MET2 2011 VCAA 3 MC

If  `x + a`  is a factor of  `4x^3 - 13x^2 - ax`  where  `a ∈ R text(\{0})`, then the value of `a` is

A.   `−4`

B.   `−3`

C.   `−1`

D.      `1`

E.      `2`

Show Answers Only

`=> B`

Show Worked Solution

`text(Let)\ \ p(x) = 4x^3 – 13x^2 – ax`

`text(If)\ \ (x + a)\ \ text(is a factor,)`

`p(−a)` `= 0`
`0` `=4(-a)^3-13(-a)^2-a(-a)`
  `=-4a^3-13a^2+a^2`
  `=-4a^2(a+3)`

 

`:. a = −3,\ \ \ (a != 0)`

`=> B`