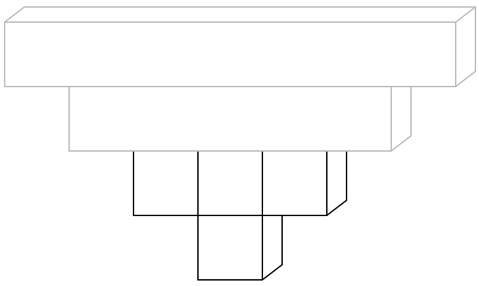
Make `y` the subject of the equation `x = sqrt(yp-1)`. (2 marks)
Financial Maths, STD2 F4 2017 HSC 28c
Michelle borrows $100 000. The interest rate charged is 12% per annum compounded monthly. The monthly payment is $1029 and the first repayment is made after one month.
What is the amount outstanding immediately after the SECOND monthly repayment is made? (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Probability, 2UG 2017 HSC 28b
Five people are in a team. Two of them are selected at random to attend a competition.
- How many different groups of two can be selected? (1 mark)
- If Mary is one of the five people in the team, what is the probability that she is selected to attend the competition? (1 mark)
Algebra, 2UG 2017 HSC 28a
Temperature can be measured in degrees Celsius (`C`) or degrees Fahrenheit (`F`).
The two temperature scales are related by the equation `F = (9C)/5 + 32`.
- Calculate the temperature in degrees Fahrenheit when it is −20 degrees Celsius. (1 mark)
- Solve the following equations simultaneously, using either the substitution method or the elimination method. (2 marks)
`qquadF = (9C)/5 + 32``qquadF = C`
- The graphs of `F = (9C)/5 + 32` and `F = C` are shown below.
What does the result from part (ii) mean in the context of the graph? (1 mark)
Algebra, 2UG 2017 HSC 30b
The cost of a jewellery box varies directly with the cube of its height.
A jewellery box with a height of 10 cm costs $50.
Calculate the cost of a jewellery box with a height of 12 cm. (2 marks)
Measurement, 2UG 2017 HSC 27d
Island `A` and island `B` are both on the equator. Island `B` is west of island `A`. The longitude of island `A` is 5°E and the angle at the centre of Earth (`O`), between `A` and `B`, is 30°.
- What is the longitude of island `B`? (1 mark)
- What time is it on island `B` when it is 10 am on island `A`? (1 mark)
- A ship leaves island `A` and travels west along the equator to island `B`. It travels at a constant speed of 40 km/h.
How long will the ship take to arrive at island `B`? Give your answer in days and hours to the nearest hour. (3 marks)
Financial Maths, STD2 F5 2017 HSC 27c
A table of future value interest factors for an annuity of $1 is shown.
An annuity involves contributions of $12 000 per annum for 5 years. The interest rate is 4% per annum, compounded annually.
- Calculate the future value of this annuity. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Calculate the interest earned on this annuity. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
FS Comm, 2UG 2017 HSC 27b
How many 20 megabyte files can fit on a 3 terabyte external hard disc? (2 marks)
Statistics, STD2 S1 2017 HSC 27a
Jamal surveyed eight households in his street. He asked them how many kilolitres (kL) of water they used in the last year. Here are the results.
`220, 105, 101, 450, 37, 338, 151, 205`
- Calculate the mean of this set of data. (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- What is the standard deviation of this set of data, correct to one decimal place? (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
Measurement, STD2 M1 2017 HSC 25 MC
Measurement, STD2 M1 2017 HSC 21 MC
The length of a netball court is measured to be 30.50 metres, correct to the nearest centimetre.
What is the lower limit for the length of the netball court?
- 30.45 m
- 30.49 m
- 30.495 m
- 30.499 m
Algebra, STD2 A2 2017 HSC 20 MC
A pentagon is created using matches.
By adding more matches, a row of two pentagons is formed.
Continuing to add matches, a row of three pentagons can be formed.
Continuing this pattern, what is the maximum number of complete pentagons that can be formed if 100 matches in total are available?
A. `25`
B. `24`
C. `21`
D. `20`
Probability, STD2 S2 2017 HSC 15 MC
The faces on a twenty-sided die are labelled $0.05, $0.10, $0.15, … , $1.00.
The die is rolled once.
What is the probability that the amount showing on the upper face is more than 50 cents but less than 80 cents?
A. `1/4`
B. `3/10`
C. `7/20`
D. `1/2`
Number and Algebra, NAP-J2-09
Measurement, NAP-J2-17
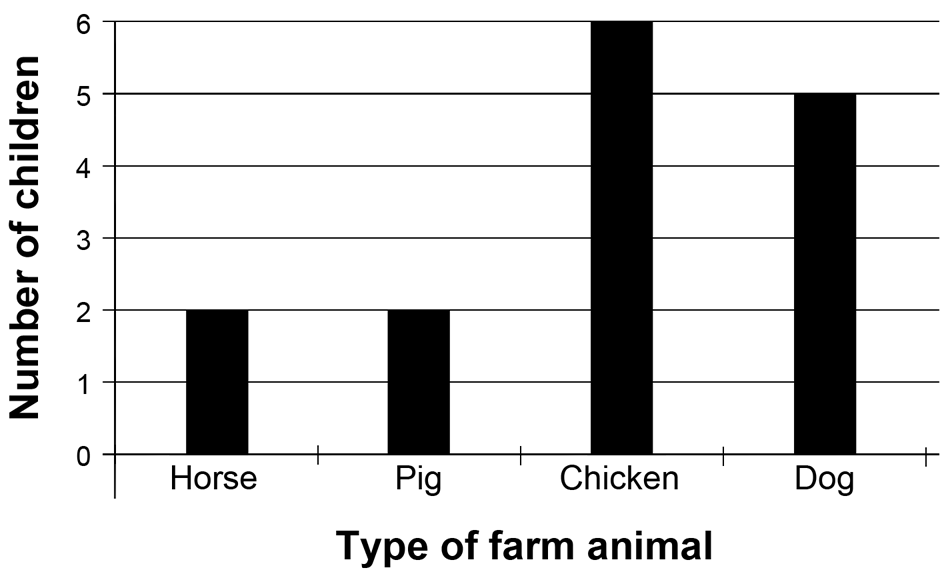
Bryan is estimating the amount of water he needs to fill up his swimming pool.
Which of these units of measurement would be the most helpful?
| cubic metres | kilograms | millilitres | centimetres | litres |
|
|
|
|
|
|
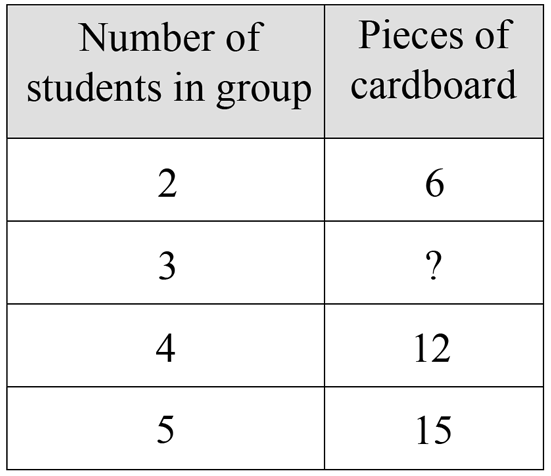
Number and Algebra, NAP-J2-14 SA
Cameron grew 146 lettuces in his vegetable garden.
A goat got into his garden and ate some lettuces, so there was only 112 lettuces left.
How many lettuces did the goat eat?
Statistics, NAP-J2-13
Number and Algebra, NAP-J2-11 SA
Number and Algebra, NAP-J2-10
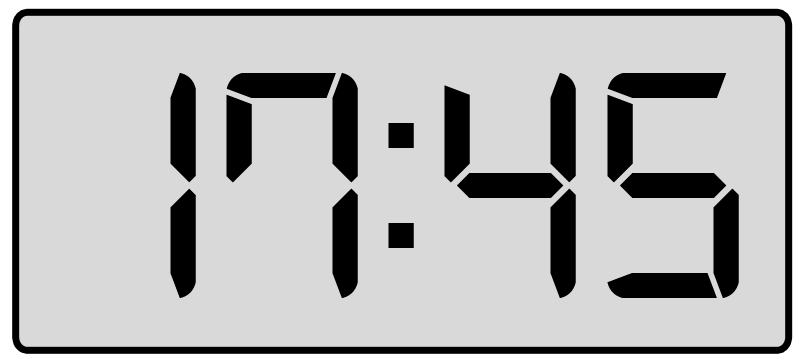
Patrick gets $7.35 in pocket money each week.
He does extra jobs one week and earns $4.75 more.
How much money did Patrick receive in total in the week?
| `$11.00` | `$11.10` | `$12.00` | `$12.10` |
|
|
|
|
|
Number, NAP-J3-NC01
Emily has 85 cents in 5-cent pieces.
How many 5-cent pieces does she have?
| `17` | `80` | `13` | `425` |
|
|
|
|
|
Measurement, NAP-J3-CA02
Measurement, NAP-J3-CA10
Bryan is estimating the amount of water he needs to fill up his swimming pool.
Which of these units of measurement would be the most helpful?
| cubic metres | kilograms | millilitres | centimetres | litres |
|
|
|
|
|
|
Quadratic, 2UA SM-Bank 10
Solve `3e^t = 5 + 8e^(−t)` for `t`. (3 marks)
Quadratic, 2UA SM-Bank 05
Solve the equation `4^x - 15 × 2^x = 16` for `x.` (3 marks)
L&E, 2ADV E1 SM-Bank 6 MC
The expression
`log_c(a) + log_a(b) + log_b(c)`
is equal to
- `1/(log_c(a)) + 1/(log_a(b)) + 1/(log_b(c))`
- `1/(log_a(c)) + 1/(log_b(a)) + 1/(log_c(b))`
- `-1/(log_a(b))-1/(log_b(c))-1/(log_c(a))`
- `1/(log_a(a)) + 1/(log_b(b)) + 1/(log_c(c))`
GEOMETRY, FUR1 SM-Bank 35 MC
Kim lives in Perth (32°S, 115°E). He wants to watch an ice hockey game being played in Toronto (44°N, 80°W) starting at 10.00 pm on Wednesday.
What is the time in Perth when the game starts?
A. 9.00 am on Wednesday
B. 7.40 pm on Wednesday
C. 9.00 pm on Wednesday
D. 12.20 am on Thursday
E. 11.00 am on Thursday
GEOMETRY, FUR2 SM-Bank 26
Two cities lie on the same meridian of longitude. One is 40° north of the other.
What is the distance between the two cities, correct to the nearest kilometre? (2 marks)
GEOMETRY, FUR2 SM-Bank 15
Osaka is at 34°N, 135°E, and Denver is at 40°N, 105°W.
- Show that there is a 16-hour time difference between the two cities.
(Ignore time zones.) (1 mark) - John lives in Denver and wants to ring a friend in Osaka. In Denver it is 9 pm Monday.
What time and day is it in Osaka then? (1 mark)
- John’s friend in Osaka sent him a text message which happened to take 14 hours to reach him. It was sent at 10 am Thursday, Osaka time.
What was the time and day in Denver when John received the text? (1 mark)
GEOMETRY, FUR2 SM-Bank 14
Pontianak has a longitude of 109°E, and Jarvis Island has a longitude of 160°W.
Both places lie on the Equator
- Find the shortest great circle distance between these two places, to the nearest kilometre. You may assume that the radius of the Earth is 6400 km. (2 marks)
- The position of Rabaul is 4° to the south and 48° to the west of Jarvis Island. What is the latitude and longitude of Rabaul? (1 mark)
Algebra, MET2 2007 VCAA 17 MC
The function `f` satisfies the functional equation `f (f (x)) = x` for the maximal domain of `f.`
The rule for the function is
- `f(x) = x + 1`
- `f(x) = x - 1`
- `f(x) = (x - 1)/(x + 1)`
- `f(x) = log_e (x)`
- `f(x) = (x + 1)/(x - 1)`
Algebra, MET2 2007 VCAA 5 MC
The simultaneous linear equations
`mx + 12y = 24`
`3x + my = m`
have a unique solution only for
- `m = 6 or m = – 6`
- `m = 12 or m = 3`
- `m in R\ text(\){– 6, 6}`
- `m = 2 or m = 1`
- `m in R\ text(\){– 12, – 3}`
Graphs, MET2 2008 VCAA 20 MC
The function `f: B -> R` with rule `f(x) = 4x^3 + 3x^2 + 1` will have an inverse function for
- `B = R`
- `B = (1/2, oo)`
- `B = (text{−∞}, 1/2]`
- `B = (text{−∞}, 1/2)`
- `B = [−1/2, oo)`
Calculus, MET2 2008 VCAA 19 MC
Algebra, MET2 2008 VCAA 12 MC
Let `f: R -> R,\ f(x) = e^x + e^(–x).`
For all `u in R,\ f(2u)` is equal to
- `f(u) + f(-u)`
- `2 f(u)`
- `(f(u))^2 - 2`
- `(f(u))^2`
- `(f(u))^2 + 2`
Graphs, MET2 2008 VCAA 9 MC
The transformation `T: R^2 -> R^2` with rule
`T([(x), (y)]) = [(4, 0), (0, -2)] [(x), (y)] + [(1), (3)]`
maps the curve with equation `y = x^3` to the curve with equation
- `y = (-(x - 1)^3)/32 + 3`
- `y = (-(4x + 1)^3 + 3)/2`
- `y = (-(x + 1)^3)/32 - 3`
- `y = ((1 - x)^3)/64 - 3`
- `y = ((4x - 1)^3 + 3)/2`
Algebra, MET2 2008 VCAA 6 MC
The simultaneous linear equations
`ax + 3y = 0`
`2x + (a + 1)y = 0`
where `a` is a real constant, have infinitely many solutions for
- `a in R`
- `a in\ text({−3, 2})`
- `a in R\ text(\ {−3, 2})`
- `a in\ text({−2, 3})`
- `a in R\ text(\ {−2, 3})`
Calculus, MET2 2008 VCAA 4 MC
If `int_1^3 f(x)\ dx = 5`, then `int_1^3 (2f(x) - 3)\ dx` is equal to
A. `4`
B. `5`
C. `7`
D. `10`
E. `16`
Calculus, MET1 SM-Bank 28
The function `f` has the rule `f(x) = 1 + 2 cos x`.
- Show that the graph of `y = f(x)` cuts the `x`-axis at `x = (2 pi)/3`. (1 mark)
--- 6 WORK AREA LINES (style=lined) ---
- Sketch the graph `y = f(x)` for `x in [-pi,pi]` showing where the graph cuts each of the axes. (2 marks)
--- 0 WORK AREA LINES (style=lined) ---
- Find the area under the curve `y = f(x)` between `x = -pi/2` and `x = (2 pi)/3`. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
Algebra, MET1 SM-Bank 24
The rule for `f` is `f(x) = e^x-e^(-x)`.
Show that the inverse function is given by
`f^(-1)(x) = log_e((x + sqrt(x^2 + 4))/2)` (3 marks)
--- 14 WORK AREA LINES (style=lined) ---
Algebra, MET1 SM-Bank 23
The function `f: [0,oo) → R` with rule `f(x) = 1/(1 + x^2)` is drawn below.
- Copy or trace this diagram into your writing booklet.
- On the same set of axes, sketch `y=f^(-1)(x)` where `f^(-1)` is the inverse function of `f(x)`. (1 mark)
--- 6 WORK AREA LINES (style=blank) ---
- Find the domain of the inverse `f^(-1)`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Find an expression for `y = f^(-1)(x)` in terms of `x`. (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
- The graphs of `y = f(x)` and `y = f^(-1)(x)` meet at exactly one point `P`.Let `α` be the `x`-coordinate of `P`. Explain why `α` is a root of the equation
- `x^3 + x-1 = 0`. (1 mark)
--- 6 WORK AREA LINES (style=lined) ---
Calculus, MET1 SM-Bank 21
The rule for function `f` is `f(x) = e^(-x^2)`. The diagram shows the graph `y = f(x)`.
The graph has two points of inflection.
- Find the `x` coordinates of these points. (2 marks)
--- 10 WORK AREA LINES (style=lined) ---
- Explain why the domain of `f(x)` must be restricted if `f(x)` is to have an inverse function. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---
- Find the rule for the inverse function `f^(-1)` if the domain of `f(x)` is restricted to `x ≥ 0.` (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
- Find the domain for `f^(-1)`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- Sketch the curve `y = f^(-1) (x)`. (1 mark)
--- 6 WORK AREA LINES (style=blank) ---
Calculus, MET1 SM-Bank 1
Algebra, MET1 SM-Bank 10
Solve the equation `log_e x-3/log_ex=2` for `x`. (3 marks)
Algebra, MET1 2011 VCAA 2b
Solve the equation `4^x - 15 × 2^x = 16` for `x.` (3 marks)
Probability, MET1 2016 VCAA 8*
Let `X` be a continuous random variable with probability density function `f(x) = {(−4xlog_e(x),0<x<=1),(0,text(elsewhere)):}` Part of the graph of `f` is shown below. The graph has a turning point at `x = 1/e`. --- 5 WORK AREA LINES (style=lined) --- --- 5 WORK AREA LINES (style=lined) ---
Probability, MET1 2016 VCAA 7
A company produces motors for refrigerators. There are two assembly lines, Line A and Line B. 5% of the motors assembled on Line A are faulty and 8% of the motors assembled on Line B are faulty. In one hour, 40 motors are produced from Line A and 50 motors are produced from Line B. At the end of an hour, one motor is selected at random from all the motors that have been produced during that hour. --- 5 WORK AREA LINES (style=lined) --- --- 4 WORK AREA LINES (style=lined) ---
Calculus, MET1 2016 VCAA 6a
Let `f : [-pi, pi] → R`, where `f (x) = 2 sin (2x)-1`.
Calculate the average rate of change of `f` between `x = -pi/3` and `x = pi/6`. (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
Graphs, MET1 2016 VCAA 5
Let `f : (0, ∞) → R`, where `f(x) = log_e(x)` and `g: R → R`, where `g (x) = x^2 + 1`.
- i. Find the rule for `h`, where `h(x) = f (g(x))`. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
ii. State the domain and range of `h`. (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
- iii. Show that `h(x) + h(-x) = f ((g(x))^2 )`. (2 marks)
--- 6 WORK AREA LINES (style=lined) ---
- iv. Find the coordinates of the stationary point of `h` and state its nature. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
- Let `k: (-∞, 0] → R` where `k (x) = log_e(x^2 + 1)`.
- i. Find the rule for `k^(-1)`. (2 marks)
--- 7 WORK AREA LINES (style=lined) ---
- ii. State the domain and range of `k^(-1)`. (2 marks)
--- 2 WORK AREA LINES (style=lined) ---
Calculus, MET1 2016 VCAA 2
Let `f: (-∞,1/2] -> R`, where `f(x) = sqrt(1-2x)`.
- Find `f^{prime}(x)`. (1 mark)
--- 3 WORK AREA LINES (style=lined) ---
- Find the angle `theta` from the positive direction of the `x`-axis to the tangent to the graph of `f` at `x =-1`, measured in the anticlockwise direction. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Probability, MET2 2009 VCAA 3
The Bouncy Ball Company (BBC) makes tennis balls whose diameters are normally distributed with mean 67 mm and standard deviation 1 mm. The tennis balls are packed and sold in cylindrical tins that each hold four balls. A tennis ball fits into such a tin if the diameter of the ball is less than 68.5 mm. --- 5 WORK AREA LINES (style=lined) --- BBC management would like each ball produced to have diameter between 65.6 and 68.4 mm. --- 5 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- --- 4 WORK AREA LINES (style=lined) --- BBC management wants engineers to change the manufacturing process so that 99% of all balls produced have diameter between 65.6 and 68.4 mm. The mean is to stay at 67 mm but the standard deviation is to be changed. --- 6 WORK AREA LINES (style=lined) ---
Calculus, MET2 2009 VCAA 2
A train is travelling at a constant speed of `w` km/h along a straight level track from `M` towards `Q.`
The train will travel along a section of track `MNPQ.`
Section `MN` passes along a bridge over a valley.
Section `NP` passes through a tunnel in a mountain.
Section `PQ` is 6.2 km long.
From `M` to `P`, the curve of the valley and the mountain, directly below and above the train track, is modelled by the graph of
`y = 1/200 (ax^3 + bx^2 + c)` where `a, b` and `c` are real numbers.
All measurements are in kilometres.
- The curve defined from `M` to `P` passes through `N (2, 0)`. The gradient of the curve at `N` is – 0.06 and the curve has a turning point at `x = 4`.
- i. From this information write down three simultaneous equations in `a`, `b` and `c`. (3 marks)
--- 3 WORK AREA LINES (style=lined) ---
- ii. Hence show that `a = 1`, `b = – 6` and `c = 16`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Find, giving exact values
- i. the coordinates of `M and P`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- ii. the length of the tunnel. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- iii. the maximum depth of the valley below the train track. (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
The driver sees a large rock on the track at a point `Q`, 6.2 km from `P`. The driver puts on the brakes at the instant that the front of the train comes out of the tunnel at `P`.
From its initial speed of `w` km/h, the train slows down from point `P` so that its speed `v` km/h is given by
`v = k log_e ({(d + 1)}/7)`,
where `d` km is the distance of the front of the train from `P` and `k` is a real constant.
- Find the value of `k` in terms of `w`. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---
- Find the exact distance from the front of the train to the large rock when the train finally stops. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
Calculus, MET2 2009 VCAA 22 MC
Consider the region bounded by the `x`-axis, the `y`-axis, the line with equation `y = 3` and the curve with equation `y = log_e (x - 1).`
The exact value of the area of this region is
A. `e^-3 - 1`
B. `16 + 3 log_e (2)`
C. `3e^3 - e^-3 + 2`
D. `e^3 + 2`
E. `3e^2`
Calculus, MET2 2009 VCAA 21 MC
A cubic function has the rule `y = f (x)`. The graph of the derivative function `f prime` crosses the `x`-axis at `(2, 0)` and `(– 3, 0)`. The maximum value of the derivative function is 10.
The value of `x` for which the graph of `y = f(x)` has a local maximum is
- `– 2`
- `2`
- `– 3`
- `3`
- `– 1/2`
Calculus, MET2 2009 VCAA 9 MC
The tangent at the point (1, 5) on the graph of the curve `y = f (x)` has equation `y = 3 + 2x.`
The tangent at the point (3, 8) on the curve `y = f (x - 2) + 3` has equation
A. `y = 2x - 4`
B. `y = x + 5`
C. `y = -2x + 14`
D. `y = 2x + 4`
E. `y = 2x + 2`
Algebra, MET2 2009 VCAA 1 MC
The simultaneous linear equations
`kx - 3y = 0`
`5x - (k + 2)y = 0`
where `k` is a real constant, have a unique solution provided
- `k in {– 5, 3}`
- `k in R\ text(\){– 5, 3}`
- `k in {– 3, 5}`
- `k in R\ text(\){– 3, 5}`
- `k in R\ text(\){0}`
Calculus, MET2 2011 VCAA 4
Deep in the South American jungle, Tasmania Jones has been working to help the Quetzacotl tribe to get drinking water from the very salty water of the Parabolic River. The river follows the curve with equation `y = x^2-1`, `x >= 0` as shown below. All lengths are measured in kilometres.
Tasmania has his camp site at `(0, 0)` and the Quetzacotl tribe’s village is at `(0, 1)`. Tasmania builds a desalination plant, which is connected to the village by a straight pipeline.
- If the desalination plant is at the point `(m, n)` show that the length, `L` kilometres, of the straight pipeline that carries the water from the desalination plant to the village is given by
- `L = sqrt(m^4-3m^2 + 4)`. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
- If the desalination plant is built at the point on the river that is closest to the village
- find `(dL)/(dm)` and hence find the coordinates of the desalination plant. (3 marks)
--- 5 WORK AREA LINES (style=lined) ---
- find the length, in kilometres, of the pipeline from the desalination plant to the village. (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
- find `(dL)/(dm)` and hence find the coordinates of the desalination plant. (3 marks)
The desalination plant is actually built at `(sqrt7/2, 3/4)`.
If the desalination plant stops working, Tasmania needs to get to the plant in the minimum time.
Tasmania runs in a straight line from his camp to a point `(x,y)` on the river bank where `x <= sqrt7/2`. He then swims up the river to the desalination plant.
Tasmania runs from his camp to the river at 2 km per hour. The time that he takes to swim to the desalination plant is proportional to the difference between the `y`-coordinates of the desalination plant and the point where he enters the river.
- Show that the total time taken to get to the desalination plant is given by
`qquadT = 1/2 sqrt(x^4-x^2 + 1) + 1/4k(7-4x^2)` hours where `k` is a positive constant of proportionality. (3 marks)
--- 6 WORK AREA LINES (style=lined) ---
The value of `k` varies from day to day depending on the weather conditions.
- If `k = 1/(2sqrt13)`
- find `(dT)/(dx)` (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- hence find the coordinates of the point where Tasmania should reach the river if he is to get to the desalination plant in the minimum time. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- find `(dT)/(dx)` (1 mark)
- On one particular day, the value of `k` is such that Tasmania should run directly from his camp to the point `(1,0)` on the river to get to the desalination plant in the minimum time. Find the value of `k` on that particular day. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Find the values of `k` for which Tasmania should run directly from his camp towards the desalination plant to reach it in the minimum time. (2 marks)
--- 5 WORK AREA LINES (style=lined) ---
Calculus, MET2 2011 VCAA 3
- Consider the function `f: R -> R, f(x) = 4x^3 + 5x-9`.
- Find `f^{prime}(x).` (1 mark)
--- 1 WORK AREA LINES (style=lined) ---
- Explain why `f^{prime}(x) >= 5` for all `x`. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---
- Find `f^{prime}(x).` (1 mark)
- The cubic function `p` is defined by `p: R -> R, p(x) = ax^3 + bx^2 + cx + k`, where `a`, `b`, `c` and `k` are real numbers.
- If `p` has `m` stationary points, what possible values can `m` have? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- If `p` has an inverse function, what possible values can `m` have? (1 mark)
--- 2 WORK AREA LINES (style=lined) ---
- If `p` has `m` stationary points, what possible values can `m` have? (1 mark)
- The cubic function `q` is defined by `q:R -> R, q(x) = 3-2x^3`.
- Write down a expression for `q^(-1)(x)`. (2 marks)
--- 4 WORK AREA LINES (style=lined) ---
- Determine the coordinates of the point(s) of intersection of the graphs of `y = q(x)` and `y = q^(-1)(x)`. (2 marks)
--- 3 WORK AREA LINES (style=lined) ---
- Write down a expression for `q^(-1)(x)`. (2 marks)
- The cubic function `g` is defined by `g: R -> R, g(x) = x^3 + 2x^2 + cx + k`, where `c` and `k` are real numbers.
- If `g` has exactly one stationary point, find the value of `c`. (3 marks)
--- 4 WORK AREA LINES (style=lined) ---
- If this stationary point occurs at a point of intersection of `y = g(x)` and `g^(−1)(x)`, find the value of `k`. (3 marks)
--- 8 WORK AREA LINES (style=lined) ---
- If `g` has exactly one stationary point, find the value of `c`. (3 marks)
Probability, MET2 2011 VCAA 2*
In a chocolate factory the material for making each chocolate is sent to one of two machines, machine A or machine B. The time, `X` seconds, taken to produce a chocolate by machine A, is normally distributed with mean 3 and standard deviation 0.8. The time, `Y` seconds, taken to produce a chocolate by machine B, has the following probability density function `f(y) = {{:(0,y < 0),(y/16,0 <= y <= 4),(0.25e^(−0.5(y-4)),y > 4):}` --- 3 WORK AREA LINES (style=lined) --- --- 3 WORK AREA LINES (style=lined) --- --- 5 WORK AREA LINES (style=lined) --- --- 5 WORK AREA LINES (style=lined) --- All of the chocolates produced by machine A and machine B are stored in a large bin. There is an equal number of chocolates from each machine in the bin. It is found that if a chocolate, produced by either machine, takes longer than 3 seconds to produce then it can easily be identified by its darker colour. --- 6 WORK AREA LINES (style=lined) ---
Calculus, MET2 2011 VCAA 1
Two ships, the Elsa and the Violet, have collided. Fuel immediately starts leaking from the Elsa into the sea.
The captain of the Elsa estimates that at the time of the collision his ship has 6075 litres of fuel on board and he also forecasts that it will leak into the sea at a rate of `(t^2)/5` liters per minute, where `t` is the number of minutes that have elapsed since the collision.
- At this rate how long, in minutes, will it take for all the fuel from the Elsa to leak into the sea? (3 marks)
--- 5 WORK AREA LINES (style=lined) ---
*Parts (b) - (d) are no longer in the syllabus.
CORE, FUR2 SM-Bank 4
Damon runs a swim school.
The value of his pool pump is depreciated over time using flat rate depreciation.
Damon purchased the pool pump for $28 000 and its value in dollars after `n` years, `P_n`, is modelled by the recursion equation below:
`P_0 = 28\ 000,qquad P_(n + 1) = P_n - 3500`
- Write down calculations, using the recurrence relation, to find the pool pump's value after 3 years. (1 mark)
--- 4 WORK AREA LINES (style=lined) ---
- After how many years will the pump's depreciated value reduce to $7000? (1 mark)
--- 5 WORK AREA LINES (style=lined) ---
The reducing balance depreciation method can also be used by Damon.
Using this method, the value of the pump is depreciated by 15% each year.
A recursion relation that models its value in dollars after `n` years, `P_n`, is:
`P_0 = 28\ 000, qquad P_(n + 1) = 0.85P_n`
- After how many years does the reducing balance method first give the pump a higher valuation than the flat rate method in part (a)? (2 marks)
--- 8 WORK AREA LINES (style=lined) ---
- « Previous Page
- 1
- …
- 59
- 60
- 61
- 62
- 63
- …
- 81
- Next Page »