SmarterEd

Aussie Maths & Science Teachers: Save your time with SmarterEd

CORE, FUR2 2021 VCAA 4

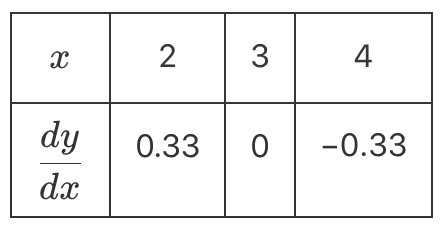
The time series plot below shows that the winning time for both men and women in the 100 m freestyle swim in the Olympic Games has been decreasing during the period 1912 to 2016.
 

Least squares lines are used to model the trend for both men and women.

The least squares line for the men's winning time has been drawn on the time series plot above.

The equation of the least squares line for men is

winning time men = 356.9 – 0.1544 × year

The equation of the least squares line for women is

winning time women = 538.9 – 0.2430 × year

  1. Draw the least squares line for winning time women on the time series plot above.   (1 mark)

  2. The difference between the women's predicted winning time and the men's predicted winning time can be calculated using the formula.
  3.       difference = winning time women – winning time men
  4. Use the equation of the least squares lines and the formula above to calculate the difference predicted for the 2024 Olympic Games.
  5. Round your answer to one decimal place.   (2 marks)

  6. The Olympic Games are held every four years. The next Olympic Games will be held in 2024, then 2028, 2032 and so on.
  7. In which Olympic year do the two least squares lines predict that the wining time for women will first be faster than the winning time for men in the 100 m freesytle?   (2 marks)

Show Answers Only
  1. `text{See Worked Solutions}`
  2. `2.7 \ text{seconds}`
  3. `2056`
Show Worked Solution

a.   

`text{Find end points for the women’s graph.}`

`1908 \ text{data point} = 538.9-0.2430 xx 1908 = 75.256`

`2020 \ text{data point} = 538.9-0.2430 xx 2020 = 48.04`

`=> \ text{Line passes through} \ (1908, 75.3) \ text{and} \ (2020, 48.0)`
 

b.   `text{difference}` `= (538.9-0.2430 xx 2024)-(356.9-0.1544 xx 2024)`
    `= 2.673 …`
    `= 2.7 \ text{seconds (to 1 d.p.)}`

 
c.    `text{Times will be equal when}`

`538.9-0.2430 xx text{year} = 356.9-0.1544 xx text{year}`

`text{year} = 2054.17 …`

`text{1st Olympic year after} \ 2054.17 = 2056`

CORE, FUR2 2021 VCAA 3

The time series plot below shows the winning time, in seconds, for the women's 100 m freestyle swim plotted against year, for each year that the Olympic Games were held during the period 1956 to 2016.

A least squares line has been fitted to the plot to model the decreasing trend in the winning time over this period.
 

The equation of the least squares line is

winning time = 357.1 – 0.1515 × year

The coefficient of determination is 0.8794

  1. Name the explanatory variable in this time series plot.   (1 mark)

  2. Determine the value of the correlation coefficient (`r`).
  3. Round your answer to three decimal places.   (1 mark)

  4. Write down the average decrease in winning time, in seconds per year, during the period 1956 to 2016.   (1 mark)

  5. The predicted winning time for the women's 100 m freestyle in 2000 was 54.10 seconds.
  6. The actual winning time for the women's 100 m freestyle in 2000 was 53.83 seconds.
  7. Determine the residual value in seconds.   (1 mark)

  8. The following equation can be used to predict the winning time for the women's 100 m freestyle in the future.
  9.      winning time =  357.1 – 0.1515 × year
  10.  i. Show that the predicted winning time for the women's 100 m freestyle in 2032 is 49.252 seconds.   (1 mark)

  11. ii. What assumption is being made when this equation is used to predict the winning time for the women's 100 m freestyle in 2032?   (1 mark)

Show Answers Only
  1. `text{year}`
  2. `- 0.938`
  3. `0.1515 \ text{seconds}`
  4. `-0.27`
  5.  i. `49.252 \ text{seconds}`
  6. ii. `text{The same trend continues when the graph is extended beyond 2016.}`
Show Worked Solution

a.      `text{year}`
 

b. `r^2` `= 0.8794 \ text{(given)}`
  `r` `= ± sqrt{0.8794}`
    `= ± 0.938 \ text{(to 3 d.p.)}`

 
`text{By inspection of graph, correlation is negative}`

`:. \ r = -0.938`
 

c.    `text{Average decrease in winning time = 0.1515 seconds}`

`text{(this is given by the slope of the line.)}`
 

d.    `text{Residual Value}` `= text{actual}-text{predicted}`
    `= 53.83-54.10`
    `= -0.27`

 

e.i.      `text{winning time (2032)}` `= 357.1-0.1515 xx 2032`
      `=49.252 \ text{seconds}`

 

e.ii.  `text{The assumption is that the graph is accurate when it is extended}`

  `text{beyond 2016 (i.e decreasing trend continues).}`

CORE, FUR2 2021 VCAA 2

The two running events in the heptathlon are the 200 m run and the 800 m run. The times taken by the athletes in these two events, times200 and time800, are linearly related.

When a least squares line is fitted to the data, the equation of this line is found to be

                      time800 = 0.03931 + 5.2756 × time200

  1. Round the values for the intercept and the slope to three significant figures. Write your answers in the boxes provided.   (1 mark)
    time800=  
     
    		   +  
     
    		   × time200
  1. The mean and the standard deviation for each variable, time200 and time800, are shown in the table below.

  1. The equation of the least squares line is
  2.     time800 = 0.03931 + 5.2756 × time200
  3. Use this information to calculate the coefficient of determination as a percentage.
  4. Round your answer to the nearest percentage.   (2 marks)

Show Answers Only
  1. `text{See Worked Solutions}`
  2. `38text{%}`
Show Worked Solution

a.    `text{time800} = 0.0393 + 5.28 xx text{time200}`

b.    `b = r xx s_y/s_x`

`text{Solve for} \ r:`

`5.2756` `= r xx 8.2910/0.96956`
`r` `= 0.6169 …`
`r^2` `= (0.6169 …)^2`
  `= 0.3806 …`
  `= 38text{% (nearest %)}`

Mechanics, SPEC2 2021 VCAA 5

A mass of `m_1` kilograms is placed on a plane inclined at 30° to the horizontal. It is connected by a light inextensible string to a second mass of `m_2` kilograms that hangs below a frictionless pulley situated at the top end of the incline, over which the string passes.
 


 

  1. Given that the inclined plane is smooth, find the relationship between `m_1` and `m_2` if the mass `m_1` moves down the plane at constant speed.  (2 marks)

The masses are now placed on a rough plane inclined at 30°, with the light inextensible string passing over a frictionless pulley in the same way, as shown in the diagram above. Let `N` be the magnitude of the normal force exerted on the mass `m_1` by the plane. A resistance force of magnitude `lambdaN` acts on and opposes the motion of the mass `m_1`.

  1. The mass `m_1` moves up the plane.
  2.   i. Mark and label all forces acting on this mass on the diagram above.  (1 mark)
  3.  ii. Taking the direction up the plane as positive, find the acceleration of the mass `m_1` in terms of `m_1`, `m_2` and `lambda`.  (2 marks)

Some time after the masses have begun to move, the mass `m_2` hits the ground at 4.5 ms`\ ^(-1)` and the string becomes slack. At this instant, the mass `m_1` is at the point `P` on the plane, which is 2 m from the pulley. Take the value of `lambda` to be 0.1

  1. How far from point `P` does the mass `m_1` travel before it starts to slide back down the plane?
  2. Give your answer in metres, correct to two decimal places.  (2 marks)
  3. Find the time taken, from when the string becomes slack, for the mass `m_1` to return to point `P`.
  4. Give your answer correct to the nearest tenth of a second.  (3 marks)
Show Answers Only
  1. `2m_2`
  2. i. 
       
     
  3. ii. `a = ((2m_2 – m_1 – lambda m_1 sqrt3)g)/(m_1 + m_2)`
  4. `s = 1.76\ text{m}`
  5. `1.7\ text{seconds}`
Show Worked Solution

a.   `m_1g sin30 – m_2g = (m_1 + m_2)a`

`text(S)text(ince)\ m_1\ text(moves at constant speed,)\ a = 0`

`m_1 g · 1/2 – m_2 g` `= 0`
`m_1` `= 2m_2`

 
b.i.   

 

b.ii.   `text(S)text(ince)\ m_1\ text(is moving up the slope)`

♦ Mean mark part (b)(ii) 43%.

`m_2g – m_1 g · 1/2 – lambdam_1 g · cos 30` `= (m_1 + m_2)a`
`m_2g – m_1 g · 1/2 – lambdam_1 g · cos sqrt3/2` `= (m_1 + m_2)a`

`:. a = ((2m_2 – m_1 – lambda m_1 sqrt3)g)/(2(m_1 + m_2))`

 

c.   `text(After)\ m_2\ text(hits the ground)`

♦♦♦ Mean mark part (c) 17%.
`m_1a` `=-m_1g*1/2 – lambda m_1 g sqrt3/2`
`a` `= -g/2(1 + lambda sqrt3)`
  `= -g/2(1 + 0.1 xx sqrt3)`

 
`text(By CAS, solve)\ \ v^2 = u^2 + 2as,\ text(for)\ \ s:`

`0 = 4.5^2 – g(1 + 0.1 xx sqrt3)s`

`s = 1.76\ text{m (to 2 d.p.)}`

 

d.   `u = 4.5\ \ text(ms)^(-1), s = 1.76\ text(m),\ a = -g/2(1 + 0.1sqrt3)`

♦♦♦ Mean mark part (d) 7%.

`text(Let)\ \ t_1 = text(Time travelling up slope until stopping)`

`s = ut_1 + 1/2at^2`

`1.76 = 4.5t_1 – 1/2 · g/2(1 + 0.1sqrt3)t_1^2`

`t_1 = 0.78\ text(seconds)`
 

`text(Let)\ t_2 =\ text(time travelling down the slope)`

`=>\ text(friction is reversed)`

`a` `= g/2(1 – 0.1sqrt3)`
`1.76` `= 0 xx t_2 + 1/2 · g/2(1 – 0.1sqrt3)  t_2^2`
`t_2` `= 0.93\ text(seconds)`

 

`:.\ text(Total time)` `= t_1 + t_2`
  `= 0.78 + 0.93`
  `= 1.7\ text{seconds (to 1 d.p.)}`

Vectors, SPEC2 2021 VCAA 4

A car that performs stunts moves along a track, as shown in the diagram below. The car accelerates from rest at point `A`, is launched into the air by the ramp `BO` and lands on a second section of track at or beyond point `C`.  This second section of track is inclined at `10^@` to the horizontal.

Due to tailwind, the effect of air resistance is negligible. Point `O` is taken as the origin of a cartesian coordinate system and all displacements are measured in metres. Point `C` has the coordinates `(16, 4)`.

At point `O`, the speed of the car is `u` ms`\ ^(-1)` and it takes off at an angle of `theta` to the horizontal direction. After the car passes point `O`, it follows a trajectory where the position of the car's rear wheels relative to point `O`, is given by

`underset~r(t) = ut cos(theta) underset~i + (ut sin(theta)-1/2 g t^2)underset~j`  until the car lands on the second section of track that starts at point `C`.
 

  1. Show that the path of the rear wheels of the car, while in the air, is given in cartesian form by
  2.    `y = x tan(theta)-(4.9x^2)/(u^2cos^2(theta))`.   (1 mark)

  3. If  `theta = 30^@`, find the minimum speed, in ms`\ ^(-1)`, that the car must reach at point `O` for the rear wheels to land on the second section of track at or beyond point `C`. Give your answer correct to two decimal places.   (2 marks)

  4. The ramp  `BO`  is constructed so that the angle `theta` can be varied.
  5. For what values of `theta` and `u` will the path of the rear wheels of the car join up smoothly with the beginning of the second section of track at point `C`? Give your answer for `theta` in degrees, correct to the nearest degree, and give your answer for `u` in ms`\ ^(-1)`, correct to one decimal place.   (3 marks)

The car accelerates from rest along the horizontal section of track `AB`, where its acceleration, `a`  ms`\ ^(-2)`, after it has travelled `s` metres from point `A`, is given by  `a = 60/v`, where `v` is its speed at `s` metres.

  1. Show that `v` in terms of `s` given by  `v = (180x)^(1/3)`.   (2 marks)

  2. After the car leaves point `A`, it accelerates to reach a speed of 20 ms`\ ^(-1)` at point `B`. However, if the stunt is called off, the car immediately brakes and reduces its speed at a rate of 9 ms`\ ^(-2)`.  It is only safe to call off the stunt if the car can come to rest at or before point `B`.  Point `W` is the furthest point along the section `AB` at which the stunt can be called off.
  3. How far is point `W` from point `B`?  Give your answer in metres, correct to one decimal place.   (3 marks)

Show Answers Only
  1. `text(Show Worked Solutions)`
  2. `17.87\ text(ms)^-1`
  3. `u = 16.4\ text(ms)^-1, \ theta = 34.1^@`
  4. `text(Show Worked Solutions)`
  5. `16.4\ text{m}`
Show Worked Solution

a.   `x = ut costheta\ …\ (1)`

`y=ut sin theta-1/2 g t^2\ …\ (2)`

`text{Using (1):}`

`t = x/(u costheta)\ …\ (3)`

`text{Substitute (3) into (2):}`

`y` `= u · x/(u costheta) sintheta-4.9 · (x^2)/(u^2cos^2theta)`
  `= x tan theta-(4.9 x^2)/(u^2 cos^2 theta)`

 

b.   `text(When)\ \ theta = 30^@`

♦ Mean mark part (b) 45%.

`y = x\ tan 30^@-(4.9 x^2)/(u^2 cos^2 30^@)`

`y = x/sqrt3-(4.9x^2)/(u^2) · 4/3`

`text{Substitute (16, 4) into equation and solve for}\ u:`

`4 = 16/sqrt3-(4.9 xx 16^2)/(u^2) · 4/3`

`u = 17.87\ text(ms)^-1\ \ text{(to 2 d.p.)}`

 

c.   `text(Smooth join will occur when)`

♦♦♦ Mean mark part (c) 12%.

`y(16) = 4\ …\ (1), \ \ text{and}`

`text(Gradient of motion equals the gradient of landing ramp)`

`(dy)/(dx)|_(x = 16) = -tan10^@\ …\ (2)`

`text{Solve (1) and (2) by CAS for}\ \ u, theta:`

`u = 16.4\ text(ms)^-1`

`theta = 34.1^@`

 

d.   `a = 60/v`

♦ Mean mark part (d) 40%.

`v · (dv)/(ds) = 60/v`

`int v^2 dv = int 60\ ds`

`1/3 v^3 = 60s + c`

`text(When)\ \ s = 0, v = 0 \ => \ c = 0`

`1/3 v^3` `= 60s`
`v^3` `= 180s`
`v` `= (180s)^(1/3)`

 

e.   `text(Find)\ s\ text{at point}\ B\ text{(by CAS):}`

♦♦♦ Mean mark part (e) 8%.
`(180s)^(1/3)` `= 20`
`s` `= (400)/9\ text(m)`

 
`text(Car decelerates at 9 ms)^(-1)`

`d/(ds)(1/2v^2)` `= -9`
`1/2 v^2` `= -9s + c`

 
`text(When)\ \ s = 400/9, v = 0 \ => \ c = 400`

`1/2 v^2` `= 400-9s`
`v` `= sqrt(800-18s)`

 
`text{Solve for}\ s\ text{(by CAS):}`

`(180s)^(1/3)` `= sqrt(800-18s)`
`s` `= 28.08`

 
`text(Distance of)\ W\ text(from)\ B`

`= 400/9-28.08`

`= 16.4\ text{m (to 1 d.p.)}`

Calculus, SPEC2 2021 VCAA 3

A thin-walled vessel is produced by rotating the graph of  `y = x^3-8`  about the `y`-axis for  `0 <= y <= H`.

All lengths are measured in centimetres.

    1. Write down a definite integral in terms of `y` and `H` for the volume of the vessel in cubic centimetres.   (1 mark)

    2. Hence, find an expression for the volume of the vessel in terms of `H`.   (1 mark)

Water is poured into the vessel. However, due to a crack in the base, water leaks out at a rate proportional to the square root of the depth `h` of water in the vessel, that is  `(dV)/(dt) = -4sqrth`, where `V` is the volume of water remaining in the vessel, in cubic centimetres, after `t` minutes.

    1. Show that  `(dh)/(dt) = (-4sqrth)/(pi(h + 8)^(2/3))`.   (2 marks)

    2. Find the maximum rate, in centimetres per minute, at which the depth of water in the vessel decreases, correct to two decimal places, and find the corresponding depth in centimetres.   (2 marks)

    3. Let  `H = 50`  for a particular vessel. The vessel is initially full and water continues to leak out at a rate of  `4 sqrth`  cm³ min`\ ^(-1)`.
    4. Find the maximum rate at which water can be added, in cubic centimetres per minute, without the vessel overflowing.   (1 mark)

  2. The vessel is initially full where  `H = 50`  and water leaks out at a rate of  `4sqrth`  cm³ min`\ ^(-1)`. When the depth of the water drops to 25 cm, extra water is poured in at a rate of  `40sqrt2`  cm³ min`\ ^(-1)`.
  3. Find how long it takes for the vessel to refill completely from a depht of 25 cm. Give your answer in minutes, correct to one decimal place.   (3 marks)

Show Answers Only
    1. `V = pi int_0^H (y + 8)^(2/3)\ dy`
    2. `V = (3pi)/5 [(H + 8)^(5/3)-32]`
    1. `text(See Worked Solutions)`
    2. `0.62\ text(cm/min when)\ \ h = 24.`
    3. `4sqrt50\ \ text(cm³/min)`
  3. `31.4\ text(mins)`
Show Worked Solution

a.i.   `y = x^3-8 \ => \ x = root3(y + 8) \ => \ x^2 = (y + 8)^(2/3)`

`:. V = pi int_0^H (y + 8)^(2/3)\ dy`

 

a.ii.   `V = (3pi)/5 [(H + 8)^(5/3)-32]`

 

b.i.   `(dV)/(dt) = -4sqrth`

`(dV)/(dh) = pi(h + 8)^(2/3) \ => \ (dh)/(dV) =1/(pi(h + 8)^(2/3))`

`(dh)/(dt)` `= (dV)/(dt) * (dh)/(dV)`
  `= (-4sqrth)/(pi(h + 8)^(2/3))`

 

b.ii.   `text(Solve)\ (d^2h)/(dt^2) = 0\ \ text(for)\ \ h\ \ text{(by CAS):}`

♦ Mean mark part (b)(ii) 42%.

`(d^2h)/(dt^2) = (2(h-24))/(3sqrth pi (h + 8)^(5/3))=0`

`=>h = 24`

`text(At)\ \ h=24, \ (dh)/(dt) = -0.62\ text(cm/min)`

`:.\ text(Max rate at which depth decreases is)`

`0.62\ text(cm/min when)\ \ h = 24.`

♦♦ Mean mark part (b)(iii) 24%.

 

b.iii.   `text(At)\ \ H = 50, text(vessel is full and losing water at)\ \ 4sqrt50\ \ text(cm³/min)`

`:. text(Water can be added at a max-rate of)\ \ 4sqrt50\ \ text(cm³/min and)`

`text(vessel will not overflow.)`

 

c.   `(dV)/(dt) = 40sqrt2-4sqrth`

♦♦♦ Mean mark part (c) 16%.

`(dV)/(dh) · (dh)/(dt) = 40sqrt2-4sqrth`

`pi(h + 8)^(2/3) · (dh)/(dt)` `= 40sqrt2-4sqrth`
`(dh)/(dt)` `= (40sqrt2-4sqrth)/(pi(h + 8)^(2/3)`
`(dt)/(dh)` `= (pi(h + 8)^(2/3))/(40sqrt2-4sqrth)`
`t` `= int (pi(h + 8)^(2/3))/(40sqrt2-4sqrth)\ dh`

 
`text(Time of vessel to refill from)\ \ h = 25\ \ text(to)\ \ h = 50:`

`t` `= int_25^50 (pi(h + 8)^(2/3))/(40sqrt2-4sqrth)\ dh`
  `~~ 31.4\ text(mins)`

Complex Numbers, SPEC2 2021 VCAA 2

The polynomial  `p(z) = z^3 + alpha z^2 + beta z + gamma`, where  `z ∈ C`  and  `alpha, beta, gamma ∈ R`, can also be written as  `p(z) = (z-z_1)(z-z_2)(z-z_3)`, where  `z_1 ∈ R`  and  `z_2, z_3 ∈ C`.

  1.  i. State the relationship between `z_2` and `z_3`.  (1 mark)

  2. ii. Determine the values of `alpha, beta` and `gamma`, given that  `p(2) = -13, |z_2 + z_3| = 0`  and  `|z_2-z_3| = 6`.  (3 marks)

Consider the point  `z_4 = sqrt3 + i`.

  1. Sketch the ray given by  `text(Arg)(z-z_4) = (5pi)/6`  on the Argand diagram below.  (2 marks)
     
  2. The ray  `text(Arg)(z-z_4) = (5pi)/6`  intersects the circle  `|z-3i| = 1`, dividing it into a major and a minor segment.
  3.  i. Sketch the circle  `|z-3i| = 1` on the Argand diagram in part b.  (1 mark)

  4. ii. Find the area of the minor segment.  (2 marks)

Show Answers Only
    1. `z_2 = barz_3`
    2. `alpha = -3, beta = 9, gamma = -27`
  2.  
     

     

c.i.   

c.ii.   `(2pi-3sqrt3)/12\ text(u²)`

Show Worked Solution

a.i.   `text(By conjugate root theory)`

`z_2 = barz_3`

 

a.ii.   `text(Let)\ \ z_1 = a + bi, \ z_2 = a-bi`

♦♦ Mean mark part (a.ii.) 35%.

`|z_2 + z_3| = |2a| = 0 \ => \ a = 0`

`|z_2-z_3| = |2b| = 6 \ => \ b = ±3`
 

`text(Using)\ \ p(2) = -13`

`(2-z_1)(2-3i)(2 + 3i)` `= -13`
`(2-z_1)(4 + 9)` `= -13`
`2-z_1` `= -1`
`z_1` `= 3`

 

`p(z)` `= (z-3)(z-3i)(z + 3i)`
  `= (z-3)(z^2 + 9)`
  `= z^3-3z^2 + 9z-27`

 
`:. alpha = –3, \ beta = 9, \ gamma = –27`

♦ Mean mark part (b) 45%.
MARKER’S COMMENT: Point of emanation is not part of required ray (see open circle).

 

b. 

 

c.i.  

 

c.ii.   `text(Arg)(z-z_4) = (5pi)/6\ \ text(cuts)\ \ ytext(-axis at angle)\ pi/3`

♦♦ Mean mark part (c.ii.) 30%.

`=>\ text(angle at centre of segment) = pi/3\ (text(equilateral triangle))`

`text(Area)` `= (pi/3)/(2pi) xx pi xx 1^2-1/2 xx 1 xx 1 xx sin (pi/3)`
  `= pi/6-sqrt3/4`
  `= (2pi-3sqrt3)/12\ text(u²)`

Calculus, SPEC2 2021 VCAA 1

Let  `f(x) = ((2x-3)(x + 5))/((x-1)(x + 2))`.

  1. Express `f(x)` in the form  `A + (Bx + C)/((x-1)(x + 2))`, where `A`, `B` an `C` are real constants.   (1 mark)

  2. State the equation of the asymptotes of the graph of `f`.   (2 marks)

  3. Sketch the graph of `f` on the set of axes below. Label the asymptotes with their equations, and label the maximum turning point and the point of inflection with their coordinates, correct to two decimal places. Label the intercepts with the coordinate axes.   (3 marks)

     

     

  4. Let  `g_k(x) = ((2x-3)(x + 5))/((x-k)(x + 2))`, where `k` is a real constant.
  5.  i. For what values of `k` will the graph of `g_k`, have two asymptotes?   (2 marks)

  6. ii. Given that the graph of `g_k` has more than two asymptotes, for what values of `k` will the graph of `g_k` have no stationary points?   (2 marks)

Show Answers Only
  1. `f(x) = 2 + (5x-11)/((x-1)(x + 2))`
  2. `text(Horizontal asymptote:)\ y = 2`

  3.  
  4.  i. `k = 3/2 => g_k(x) = 2 + 6/(x + 2)`
  5. ii. `k , -5\ \ text(or)\ \ k > 3/2`
Show Worked Solution

a.   `text{By CAS  (prop Frac}\ f(x)):`

`f(x) = 2 + (5x-11)/((x-1)(x + 2))`
 

b.   `text(Vertical asymptotes:)\ x = 1, x = –2`

`text(As)\ \ x -> ∞, y -> 2`

`text(Horizontal asymptote:)\ y = 2`

♦ Mean mark part (c) 48%.

 
c.   

 

d.i.   `text(Two asymptotes only when:)`

♦♦ Mean mark part (d)(i) 24%.

`k = -2 \ => \ g_k(x) = 2-(23 + x)/((x + 2)^2)`

`k = -5 \ => \ g_k(x) = 2-7/(x + 2)`

`k = 3/2 \ => \ g_k(x) = 2 + 6/(x + 2)`

 

d.ii.   `text(By CAS, solve)\ \ d/(dx)(g_k(x)) = 0\ \ text(for)\ \ x:`

♦♦♦ Mean mark part (d)(ii) 16%.

`x = (-4k + 15 ± sqrt(-21(2k^2 + 7k-15)))/(2k + 3)`
 

`text(No solutions occur when:)`

`k = -3/2\ \ text(or)`

`2k^2 + 7k-15 < 0`

`=> k < -5\ \ text(or)\ \ k > 3/2`

Calculus, MET2 2021 VCAA 5

Part of the graph of  `f: R to R , \ f(x) = sin (x/2) + cos(2x)`  is shown below.
 

  1. State the period of `f`.   (1 mark)

  2. State the minimum value of `f`, correct to three decimal places.   (1 mark)

  3. Find the smallest positive value of `h` for which  `f(h-x) = f(x)`.   (1 mark)
Consider the set of functions of the form  `g_a : R to R, \ g_a (x) = sin(x/a) + cos(ax)`, where `a` is a positive integer.
  1. State the value of `a` such that  `g_a (x) = f(x)`  for all `x`.   (1 mark)

  2. i.  Find an antiderivative of `g_a` in terms of `a`.   (1 mark)

  3. ii. Use a definite integral to show that the area bounded by `g_a` and the `x`-axis over the interval  `[0, 2a pi]`  is equal above and below the `x`-axis for all values of `a`.  (3 marks)

  4. Explain why the maximum value of `g_a` cannot be greater than 2 for all values of `a` and why the minimum value of `g_a` cannot be less than –2 for all values of `a`.   (1 mark)

  5. Find the greatest possible minimum value of `g_a`.   (1 mark)

Show Answers Only
  1. `4 pi`
  2. `-1.722`
  3. `2 pi`
  4. `text{See Worked Solutions}`
  5. i.  `text{See Worked Solutions}`
    ii. `text{See Worked Solutions}`
  6. `text{See Worked Solutions}`
  7. `-sqrt2`
Show Worked Solution

a.    `text{By inspection, graph begins to repeat after 4pi.}`

`text{Period}\ = 4 pi`
 

b.    `text{By CAS: Sketch}\ \ f(x) = sin (x/2) + cos(2x)`

`f_min = -1.722`

♦ Mean mark part (c) 21%.
 

c.     `text{If} \ \ f(x)\ \ text{is reflected in the} \ y text{-axis and translated} \ 2 pi \ text{to the right} => text{same graph}`

`f(x) = f(-x + h) = f(2 pi-x)`

`:. h = 2 pi`
 

d.    `f(x) = sin(x/2) + cos(2x)`

`g_a(x) = sin(x/a) + cos(2a)`

`g_a(x) = f(x) \ \ text{when} \ \ a = 2`
 

e.i.  `int g_a (x)\ dx`

♦ Mean mark part (e)(i) 50%.

`= -a cos (x/a) + {sin (ax)}/{a} , \ (c = 0)`
 

e.ii.   `int_0^{2a pi} g_a(x)\ dx`

♦ Mean mark part (e)(ii) 29%.

`= {sin (2a^2 pi)}/{a}`

`= 0 \ \ (a ∈ ZZ^+)`
 

`text{When integral = 0, areas above and below the} \ x text{-axis are equal.}`
 

f.    `g_a (x) = sin(x/a) + cos (ax)`

♦ Mean mark part (f) 13%.

`-1 <= sin(x/a) <= 1 \ \ text{and}\ \ -1 <= cos(ax) <= 1`

`:. -2 <= g_a (x) <= 2`
 

g.    `text{Sketch}\ \ g_a (x) \ \ text{by CAS}`

♦ Mean mark part (g) 2%.

`text{Minimum access at}\ \ a = 1`

`g_a(x)_min = – sqrt2`

Probability, MET2 2021 VCAA 4

A teacher coaches their school's table tennis team.

The teacher has an adjustable ball machine that they use to help the players practise.

The speed, measured in metres per second, of the balls shot by the ball machine is a normally distributed random variable `W`.

The teacher sets the ball machine with a mean speed of 10 metres per second and standard deviation of 0.8 metres per second.

  1. Determine  `text(Pr) (W ≥11)`, correct to three decimal places.   (1 mark)

  2. Find the value of `k`, in metres per second, which 80% of ball speeds are below. Give your answer in metres per second, correct to one decimal place.   (1 mark) 

The teacher adjusts the height setting for the ball machine. The machine now shoots balls high above the table tennis table.

Unfortunately, with the new height setting, 8% of balls do not land on the table.

Let  `overset^P`  be the random variable representing the sample proportion of the balls that do not land on the table in random samples of 25 balls.

  1. Find the mean and the standard deviation of  `overset^P`.   (2 marks)

  2. Use the binomial distribution to find  `text(Pr) (overset^P > 0.1)`, correct to three decimal places.   (2 marks) 

The teacher can also adjust the spin setting on the ball machine.

The spin, measured in revolutions per second, is a continuous random variable  `X` with the probability density function
 

       `f(x) = {(x/500, 0 <= x < 20), ({50-x}/{750}, 20 <= x <= 50), (\ 0, text(elsewhere)):}`
 

  1. Find the maximum possible spin applied by the ball machine, in revolutions per second.   (1 mark)

Show Answers Only

  1. `0.106`
  2. `0.8`
  3. `sqrt46/125`
  4. `0.323`
  5. `50 \ text{revolutions per second}`
  6. This content is no longer in the Study Design.
  7. This content is no longer in the Study Design.
  8. This content is no longer in the Study Design.

Show Worked Solution

a.   `W\ ~\ N (10,0.8^2)`

`text{By CAS: norm Cdf} \ (11, ∞, 10, 0.8)`

`text(Pr) (W >= 11) = 0.106`
 

b.    `text(Pr) (W < k) = 0.8 \ \ \ text{By CAS: inv Norm} \ (0.8, 10, 0.8)`
 

c.    `E(overset^P) =  0.08 = 2/25`

♦ Mean mark part (c) 45%.

`text(s.d.) (overset^P) = sqrt{{0.08 xx 0.92}/{25}} = sqrt46/125`
 

d.    `X\ ~\ text(Bi) (25, 0.08)`

♦ Mean mark part (d) 49%.

`text{By CAS: binomCdf} \ (25, 0.08, 3, 25)`

`text(Pr) (overset^P > 0.1)` `= text(Pr) (X > 0.1 xx 25)`
  `= text(Pr) (X > 2.5)`
  `= text(Pr) (X >= 3)`
  `= 0.323`

 

e.    `text{Maximum spin = 50 revolutions per second}`

♦♦ Mean mark part (e) 21%.

 

f.    This content is no longer in the Study Design.

g.    This content is no longer in the Study Design.

h.    This content is no longer in the Study Design.

Calculus, MET2 2021 VCAA 3

Let  `q(x) = log_e (x^2-1)-log_e (1-x)`.

  1. State the maximal domain and the range of `q`.   (2 marks)

  2.  i. Find the equation of the tangent to the graph of `q` when  `x =-2`.   (1 mark)

  3. ii. Find the equation of the line that is perpendicular to the graph of `q` when  `x =-2`  and passes through the point  (-2, 0).   (1 mark)

Let  `p(x) = e^{-2x}-2e^-x + 1.`

  1. Explain why `p` is not a one-to one function.   (1 mark)

  2. Find the gradient of the tangent to the graph of `p` at  `x = a`.   (1 mark)

The diagram below shows parts of the graph of `p` and the line  `y = x + 2`.
 
 
                     
 
The line  `y = x + 2`  and the tangent to the graph of `p` at  `x = a`  intersect with an acute angle of `theta` between them.

  1. Find the value(s) of `a` for which  `theta = 60^@`. Give your answer(s) correct to two decimal places.   (3 marks)

  2. Find the `x`-coordinate of the point of intersection between the line  `y = x + 2` and the graph of `p`, and hence find the area bounded by  `y = x + 2`, the graph of `p` and the `x`-axis, both correct to three decimal places.   (3 marks)

Show Answers Only
  1. `text{Domain:} \ x ∈ (-∞, -1)`
    `text{Range:} \ y ∈ R`
  2. i.  `-x-2`
    ii. `x + 2`
  3. `text{Not a one-to-one function as it fails the horizontal line test.}`
  4. `-2e^{-2a} + 2e^{-a}`
  5. `-0.67`
  6. `1.038\ text(u)^2`
Show Worked Solution

a.    `text(Method 1)`

`x^2-1 > 0 \ \ => \ \ x > 1 \ \ ∪ \ \ x < -1`

`1-x > 0 \ \ => \ \ x < 1`
 
`:. \ x ∈ (-∞, -1)`
 

`text(Method 2)`

`text{Sketch graph by CAS}`

`text{Asymptote at} \ x = -1`

`text{Domain:} \ x ∈ (-∞, -1)`

`text{Range:} \ y ∈ R`
 
 

b.     i.   `text{By CAS (tanLine} \ (q (x), x, -2)):`

`y = -x-2`
 

ii.   `text{By CAS (normal} \ (q (x), x, -2)):`

`y = x + 2`
  

c.    `text{Sketch graph by CAS.}`

`p(x) \ text{is not a one-to-one function as it fails the horizontal line test}`

`text{(i.e. it is a many-to-one function)}`
 

d.   `p^{′}(x) = -2e^{-2x} + 2e^-x`

`p^{prime}(a) = -2e^{-2a} + 2e^{-a}`
 
 

e. 

 
`text{Case 1}`

`text{By CAS, solve:}`

`2e^{-a} -2e^{-2a} =-tan (15^@) \ \ text{for}\ a:`

`a = -0.11`
 

`text{Case 2}`

`text{Case 1}`

`text{By CAS, solve:}`

`2e^{-a}-2e^{-2a} = -tan 75^@\ \ text{for}\ a:`

`a = -0.67`
 

f.     `text{At intersection,}`

`x + 2 = e^{-2x} -2e^{-x} + 1`

`x = -0.750`
 

`text{Area}` `= int_{-2}^{-0.750} x + 2\ dx + int_{-0.750}^0 e^{-2x}-2e^{-x} + 1\ dx`
  `= 1.038 \ text(u)^2`

Calculus, MET2 2021 VCAA 1

A rectangular sheet of cardboard has a width of `h` centimetres. Its length is twice its width.

Squares of side length `x` centimetres, where  `x > 0`  are cut from each of the corners, as shown in the diagram below.
 

The sides  of this sheet of cardboard are then folded up to make a rectangular box with an open top, as shown in the diagram below.

Assume that the thickness of the cardboard is negligible and that  `V_text{box} > 0`.
 

A box is to be made from a sheet of cardboard with  `h` = 25 cm.

  1. Show that the volume, `V_text{box} > 0`, in cubic centimetres, is given by  `V_text{box} (x) = 2x (25-2x)(25-x)`.   (1 mark)

  2. State the domain of  `V_text{box}`.   (1 mark)

  3. Find the derivative of  `V_text{box}`  with respect to `x`.   (1 mark)

  4. Calculate the maximum possible volume of the box and for which value of `x` this occurs.   (3 marks)

  5. Waste minimisation is a goal when making cardboard boxes.
  6. Percentage wasted is based on the area of the sheet of cardboard that is cut out before the box is made.
  7. Find the percentage of the sheet of cardboard that is wasted when `x = 5`.   (2 marks)

Now consider a box made from a rectangular sheet of cardboard where  `h>0` and the box's length is still twice its width.

    1. Let  `V_text{box}` be the function that gives the volume of the box.
    2. State the domain `V_text{box}` in terms of `h`.   (1 mark)

    3. Find the maximum volume for any such rectangular box, `V_text{box}`, in terms of  `h`.   (3 marks)

  2. Now consider making a box from a square sheet of cardboard with side lengths of `h` centimetres.
  3. Show that the maximum volume of the box occurs when  `x = h/6`.   (2 marks)

Show Answers Only
  1. `text{Show Worked Solutions}`
  2. `(0, 12.5)`
  3. `text{Show Worked Solutions}`
  4. `{15625 sqrt3}/{9}  \ text{or} \ {15625}/{3 sqrt3}`
  5. `8%`
  6. i.  `text{Domain} \ (V_text{box}) = (0, h/2)`
  7. (sqrt3 h^3)/9`
  8. `text(See Worked Solutions)`
Show Worked Solution
a.   `V` `= x (h-2x)(2h-2x)`
    `= x (25-2x)(50-2x)`
    `= 2x (25-2x)(25-x)`

 

b.   `text{Sketch} \ y = 2x (25-2x)(25-x) \ text{by CAS:} `

♦ Mean mark (b) 42%.

`text{Domain is} \ (0, 12.5)`
 

c.    `(dV)/dx = 12x^2-300x + 1250`
 

d.    `text{Solve} \ V^{′}(x) = 0 \ text{for} \ x :`

`x = {-25 (sqrt3-3)}/6 \ or \ x = {25(sqrt3 + 3)}/6`

`:. \ x =  {-25 (sqrt3-3)}/6 \ , \ \ x ∈ (0, 12.5)`

`:. \ V_text{max} = {15\ 625 sqrt3}/9  \ text{or} \  \ {15\ 625}/{3 sqrt3}`
 

e.   `text{Area cut out} = 4 xx 5^2 = 100\ text(cm)^2`

`text{% Wasted}` `= {100}/{25 xx 50} xx 100`
  `= 8text(%)`

♦ Mean mark (f.i.) 33%.

 
f.i.  `text{Domain} \ (V_text{box}) = (0, h/2), \ \ text{(using part b)}`
 

f.ii.  `V = x (h-2x)(2h-2x)`

♦ Mean mark (f.ii.) 45%.

`text{Solve} \ V^{′}(x) = 0 \ text{for} \ x:`

`x = {-h (sqrt3-3)}/{6} \ \ text{or} \ \ x = {h(sqrt{3} + 3)}/{6}`

`V_text{max} \ text{occurs when} \ \ x = {-h(sqrt3-3)}/{6} \ \ text{(see part a)}`

`V_text{max} = (sqrt3 h^3)/9`

 

g.    `V = x(h-2x)(h-2x)`

♦ Mean mark part (g) 40%.

`text{Solve} \ V^{′}(x) = 0 \ text{for} \ x:`

`x = h/2 \ \ text{or} \ \ x =  h/6`

`V (h/6) = {2h^3}/{27} \ , \ V(h/2) = 0`

`:. V_text{max} \ text{occurs when} \ \ x = {h}/{6}`

Calculus, MET2 2021 VCAA 19 MC

Which one of the following functions is differentiable for all real values of `x`?

  1. `f(x) = {{:(qquadx),(–x):} {:(qquadx<0),(qquadx≥0):}`
  2.  `f(x) = {{:(qquadx),(–x):} {:(qquadx<0),(qquadx>0):}`
  3.  `f(x) = {{:(8x + 4),((2x + 1)^2):} {:(qquadx<0),(qquadx≥0):}`
  4.  `f(x) = {{:(2x + 1),((2x + 1)^2):} {:(qquadx<0),(qquadx≥0):}`
  5.  `f(x) = {{:(4x + 1),((2x + 1)^2):} {:(qquadx<0),(qquadx≥0):}`
Show Answers Only

`E`

Show Worked Solution

`text{Differentiable → function must be continuous and smooth}`

♦♦ Mean mark 35%.

`text{Consider}\ E:`
 

`f(x) = {{:(4x + 1),((2x + 1)^2):} {:(qquadx<0),(qquadx≥0):}  \ => \ f′(x) = {{:(4),(4(2x + 1)):} {:(qquadx<0),(qquadx≥0):}`
 

`text{As} \ x to 0^- \ , \ f(x) to \ 1 \ , \ f′(x) = 4`

`text{As} \ x to 0^+ \ , \ f(x) to \ 1 \ , \ lim f′(x) = 4`

`:. \ text{Function is continuous and smooth}`

`=> E`

Graphs, MET2 2021 VCAA 18 MC

Let  `f : R to R, \ f(x) = (2x - 1)(2x + 1)(3x - 1)`  and  `g : (–∞, 0) to R, \ g(x) = x log_e(–x)`.

The maximum number of solutions for the equation  `f(x - k) = g(x)`, where  `k ∈ R`, is

  1. 0
  2. 1
  3. 2
  4. 3
  5. 4
Show Answers Only

`D`

Show Worked Solution

`text{By CAS, graph}`

♦ Mean mark 39%.

`f(x) = (2x – 1)(2x + 1)(3x – 1) , text{and}`

`g(x) = x log_e (-x) , x < 0`
 


 

`text{If} \ f(x) \ text{is translated to the left, by inspection,}`

`text{a maximum of 3 intersections can occur.}`
 

`=> \ D`

Algebra, MET2 2021 VCAA 16 MC

Let  `cos (x) = 3/5`  and  `sin^2(y) = 25/169`, where  `x ∈ [{3pi}/{2} , 2 pi]`  and  `y ∈ [{3pi}/{2} , 2 pi]`.

The value of  `sin(x) + cos(y)`  is 

  1. `8/65`
  2. `– 112/65`
  3. `112/65`
  4. `–8/65`
  5. `64/65`
Show Answers Only

`A`

Show Worked Solution

`text{Both angles are in 4th quadrant (given)}`

♦♦ Mean mark 31%.

`cos(x) = 3/5`
 

`sin(x)` `= – 4/5\ \ text{(4th quadrant)}`
`sin^2(y)` `= 25/169`
`sin(y)` `= – 5/13\ \ text{(4th quadrant)}`

 

`cos(y) = 12/13`
 

`:. \ sin(x) + cos(y)` `= – 4/5 + 12/13`
  `= 8/65`

`=> A`

Probability, MET2 2021 VCAA 15 MC

Four fair coins are tossed at the same time.

The outcome for each coin is independent of the outcome for any other coin.

The probability that there is an equal number of heads and tails, given that there is at least one head; is

  1. `1/2`
  2. `1/3`
  3. `3/4`
  4. `2/5`
  5. `4/7`
Show Answers Only

`D`

Show Worked Solution

`X\ ~\ text(Bi) (4, 1/2)`

♦ Mean mark 48%.

`text(By CAS):`

`text(Pr) (X = 2 | X ≥ 1)` `= {text(Pr) (X = 2)}/{text(Pr) (X ≥ 1)}`
  `= 0.375/0.9375`
  `= 2/5`

`=> D`

Calculus, MET2 2021 VCAA 8 MC

The graph of the function  `f`  is shown below.
 

The graph corresponding to  `f^{′}` is
 


 


 

Show Answers Only

`E`

Show Worked Solution

`text(By elimination:)`

♦ Mean mark 40%.

`text{As} \ \ x to a^+ \ , \ f^{′}(x) to ∞`

`:. \ text{Eliminate}\ A, B, C`

`f(x) \ text{exists for} \ x ∈ (a,∞)`

`f^{′}(x) \ text{only exists for} \ \ x ∈ (a, ∞)`

`:. \ text{Eliminate}\ D`

`=> E`

Statistics, SPEC2 2021 VCAA 20 MC

An office has two coffee machines that operate independently of each other. The time taken for each machine to produce a cup of coffee is normally distributed with a mean of 30 seconds and a standard deviation of 5 seconds. On a particular morning, a cup is produced from each machine.

The probability that the time taken by each coffee machine to produce one cup of coffee will differ by less than 3 seconds is closest to

  1. 0.164
  2. 0.236
  3. 0.329
  4. 0.451
  5. 0.671
Show Answers Only

`C`

Show Worked Solution

`T_n~N(30, 5^2), n = 1, 2\ …`

♦ Mean mark 43%.

`E(T_2-T_1) = 0`

`text(Var)(T_2-T_1)` `= text(Var)(T_2) + text(Var)(T_1)`
  `= 2 xx 5^2`
  `= 50`

 
`:. T_2-T_1~N(0, (sqrt50)^2)`

`text(Pr)(-3 < T_2-T_1 < 3) = 0.329`

`text{By CAS: normCdf}(–3,3,0,sqrt50)`

`=>\ C`

Statistics, SPEC2 2021 VCAA 19 MC

The mean unscaled score for a certain assessment task is 25 and the variance is 36. The scores scaled so that the mean score is 30 and the variance is 49. Let `S` be the scaled scores, to the nearest integer, and let `X` be the unscaled scores.

If the scaling function takes the form  `S = mX+n`, where  `m ∈ R^+` and `n ∈ R`, then a score of 32 would be scaled to

  1. 22
  2. 34
  3. 36
  4. 38
  5. 40
Show Answers Only

`D`

Show Worked Solution
`E(S)` `= E(mX + n)`
  `= mE(X) + n`
  `= 25m + n`

 

♦ Mean mark 51%.
`text(Var)(S)` `= text(Var)(mX + n)`
  `= m^2text(Var)(X)`
  `= 36m^2`

 
`text{Solve (by CAS)}:`

`25m + n` `= 30\ …\ (1)`
`36m^2` `= 49\ …\ (2)`

 
`m = 7/6, n = 5/6`
 

`:.\ text(Adjusted score of 32)`

`= 7/6 xx 32 + 5/6`

`~~ 38`

`=>\ D`

Statistics, SPEC2 2021 VCAA 17 MC

Bottles of a particular brand of soft drink are labelled as having a volume of 1.25 L. The machines filling the bottles deliver a volume that is normally distributed with a mean of 1.26 L and a standard deviation of 0.01 L.

The probability that six bottles have a mean volume that is at least the labelled volume of 1.25 L is closest to

  1. 0.5968
  2. 0.8413
  3. 0.9750
  4. 0.9772
  5. 0.9928
Show Answers Only

`E`

Show Worked Solution

`V~N (1.26, 0.01^2)`

♦ Mean mark 50%.

`E(barV) = mu = 1.26`

`text(s.d.)(barV) = 0.01/sqrt6`

`text(Pr)(barV>= 1.25) ≈ 0.9928`

`text{By CAS: normCdf}(1.25,∞,1.26,0.01/sqrt6)`

`=> E`

Mechanics, SPEC2 2021 VCAA 16 MC

An object of mass `m` kilograms slides down a smooth slope that is inclined at an angle of `theta^@` to the horizontal, where  `0^@ < theta^@ < 45^@`. The acceleration of the object down the slope is  `a\ text(ms)^(-2), a > 0`.

If the angle of inclination of the slope is doubled to `2theta^@`, then the acceleration of the object down the slope, in `text(ms)^(-2)`, is

  1. `2a`
  2. `(2a)/gsqrt(g^2 - a^2)`
  3. `(2a^2 - g^2)/g`
  4. `a/g sqrt(g^2 - a^2)`
  5. `2asqrt(g^2 - a^2)`
Show Answers Only

`B`

Show Worked Solution

`ma = mgsintheta`

♦ Mean mark 48%.
`sintheta` `= a/g`
`cos^2theta` `= 1 – (a^2)/(g^2)`
`costheta` `= sqrt(1 – (a^2)/(g^2))`

 
`text(If incline angle) = 2theta`

`ma` `= mgsin(2theta)`
`a` `= g*2sinthetacostheta`
  `= g *2* a/g sqrt(1 – (a^2)/(g^2))`
  `= (2a)/g sqrt(g^2 – a^2)`

 
`=>\ B`

Vectors, SPEC2 2021 VCAA 13 MC

The scalar resolute of vector  `underset~a`  in the direction of vector  `underset~b`  is  `-4`.

If  `underset~b = – sqrt3 underset~i`,  the vector resolute of  `underset~a`  in the direction of  `underset~b`  is

  1. `-4underset~i`
  2. `-3underset~i`
  3. `1/sqrt3 underset~i`
  4. `3underset~i`
  5. `4underset~i`
Show Answers Only

`E`

Show Worked Solution

`text(Scalar resolute of)\ underset~a\ text(is direction of)\ underset~b = -4`

♦ Mean mark 48%.

`underset~a · overset^underset~b = -4`

`underset~b = -sqrt3 underset~i \ => \ overset^underset~b = -underset~i`

`text(Vector resolute of)\ underset~a\ text(in direction of)\ underset~b`

`(underset~a · overset^underset~b)overset^underset~b = 4underset~i`

`=>\ E`

Calculus, SPEC2 2021 VCAA 9 MC

Which one of the following derivatives corresponds to a graph of  `f`  that has no points of inflection?

  1. `f′(x) = 2(x - 3)^2 + 5`
  2. `f′(x) = 2(x - 3)^3 + 5`
  3. `f′(x) = 5/2(x - 3)^2`
  4. `f′(x) = 1/2(x - 3)^2 - 5`
  5. `f′(x) = (x - 3)^3 - 12x`
Show Answers Only

`B`

Show Worked Solution

`text(If no POI,)\ \ f″(x)\ text(does not change sign).`

♦ Mean mark 38%.

`text(Consider option B)`

`f″(x) = 6(x – 3)^2 \ ->\ text(doesn’t change sign)`

`=>\ B`

Trigonometry, SPEC2 2021 VCAA 7 MC

A relation is defined parametrically by

\(x(t)=5 \cos (2 t)+1, \quad y(t)=5 \sin (2 t)-1\)

If  \(A(6,-1)\)  and  \(B(1,4)\)  are two points that lie on the graph of the relation, then the shortest distance along the graph from \(A\) to \(B\) is

  1. \(\dfrac{\pi}{4}\)
  2. \(\dfrac{\pi}{2}\)
  3. \(\pi\)
  4. \(\dfrac{5 \pi}{4}\)
  5. \(\dfrac{5 \pi}{2}\)
Show Answers Only

\(E\)

Show Worked Solution

\(x=5 \cos (2 t)+1 \Rightarrow \cos (2 t)=\dfrac{x-1}{5}\)

♦ Mean mark 39%.

\(y=5 \sin (2 t)-1 \Rightarrow \sin (2 t)=\dfrac{y+1}{5}\)

\((\cos (2 t))^2+(\sin (2 t))^2\) \(=1\)  
\((x-1)^2+(y+1)^2\) \(=25\)  

 

\(\text {Distance}\ =\dfrac{1}{4} \times 2 \times \pi \times r =\dfrac{5 \pi}{2}\)

\(\Rightarrow E\)

Complex Numbers, SPEC2 2021 VCAA 5 MC

The graph of the circle given by  `|z - 2 - sqrt3i| = 1`, where  `z ∈ C`, is shown below.
 


 

For points on this circle, the maximum value of  `|z|`  is

  1. `sqrt3 + 1`
  2. `3`
  3. `sqrt13`
  4. `sqrt7 + 1`
  5. `8`
Show Answers Only

`D`

Show Worked Solution
♦ Mean mark part 42%.

`text(Centre of circle at)\ (2, sqrt3)`

`text(Radius = 1)`

`text(By Pythagoras, line from)`

`text(origin to centre of circle)`

`d = sqrt(2^2 + sqrt(3)^2) = sqrt7`

`:. |z|\ text(max) = sqrt7 + 1`

`=>\ D`

Complex Numbers, SPEC2 2021 VCAA 4 MC

For  `z ∈ C`, if  `text(Im)(z) > 0`, then  `text(Arg)((zbarz)/(z - barz))` is

  1. `-pi/2`
  2. `0`
  3. `pi/4`
  4. `pi/2`
  5. `pi`
Show Answers Only

`A`

Show Worked Solution

`text(Let)\ \ z=x+iy \ => \ barz=x-iy`

♦♦ Mean mark 35%.
`text(Arg)((zbarz)/(z – barz))` `= text(Arg)(zbarz) – text(Arg)(z – barz)`
  `= text(Arg)(x^2 + y^2) – text(Arg)(2yi)`
  `= 0 – text(Arg)(2yi),\ \ text(where)\ y > 0`
  `= -pi/2`

`=>\ A`

Vectors, SPEC1 2021 VCAA 9

Let  `underset~r(t) = (-1 + 4cos(t))underset~i + 2/sqrt3\ sin(t)underset~j`  and  `underset~s(t) = (3 sec(t)-1)underset~i + tan(t)underset~j`  be the position vectors relative to a fixed point `O` of particle `A` and particle `B` respectively for  `0 <= 1 <= c`, where `c` is a positive real constant.

    1. Show that the cartesian equation of the path of particle `A` is  `((x + 1)^2)/16 + (3y^2)/4 = 1`.   (1 mark)

    2. Show that the cartesian equation of the path of particle `A` in the first quadrant can be written as  `y = sqrt3/6 sqrt(-x^2-2x + 15)`.   (1 mark)

    1. Show that the particles `A` and `B` will collide.   (1 mark)

    2. Hence, find the coordinates of the point of collision of the two particles.   (1 mark)

    1. Show that  `d/(dx)(8arcsin ((x + 1)/4) + ((x + 1)sqrt(-x^2 -2x + 15))/2) = sqrt(-x^2-2x + 15)`.   (2 marks)


    2.    

      Hence, find the area bounded by the graph of  `y = sqrt3/6 sqrt(-x^2-2x + 15)`,  the `x`-axis and the lines  `x = 1`  and  `x = 2sqrt3-1`,  as shown in the diagram above. Give your answer in the form  `(asqrt3pi)/b`, where `a` and `b` are positive integers.   (2 marks)

Show Answers Only
    1. `text(See Worked Solutions)`
    2. `text(See Worked Solutions)`
    1. `text(See Worked Solutions)`
    2. `-1 + 2sqrt3, 1/sqrt3`
    1. `text(See Worked Solutions)`
    2. `(2sqrt3pi)/9`
Show Worked Solution

a.i.   `text(Particle A)`

`underset~r(t) = (-1 + 4cos(t))underset~i + 2/sqrt3\ sin(t)underset~j`

`x` `= -1 + 4cos(t)`
`x + 1` `= 4cos(t)`
`cos(t)` `= (x + 1)/4`
`y` `= 2/sqrt3\ sin(t)`
`sin(t)` `= (sqrt3 y)/2`

 
`text(Using)\ \ cos^2(t) + sin^2(t) = 1`

`((x + 1)^2)/16 + (3y^2)/4 = 1`

 

a.ii.  `((x + 1)^2)/16 + (3y^2)/4 = 1`

♦ Mean mark part (a)(ii) 41%.
`(x + 1)^2 + 12y^2` `= 16`
`12y^2` `= 16-x^2-2x-1`
`y^2` `= 1/12(15-x^2-2x)`
`y` `= ±sqrt(1/12 (-x^2-2x + 15))`

 
`text(In the 1st quadrant,)\ \ y > 0`

`:. y` `= 1/sqrt12 sqrt(-x^2-2x + 15)`
  `= 1/(2sqrt3) xx sqrt3/sqrt3 sqrt(-x^2-2x + 15)`
  `= sqrt3/6 sqrt(-x^2-2x + 15)`

 

b.i.   `text(If particles collide, find)\ \t\ text(that satisfies)`

`-1 + 4cos(t)` `= 3sec(t)-1\ \ text(and)`
`2/sqrt3 sin(t)` `= tan(t)`

 
`text(Equate)\ underset~j\ text(components:)`

`2/sqrt3 sin(t)` `= (sin(t))/(cos(t))`
`cos(t)` `= sqrt3/2`
`t` `= pi/6`

 
`text(Check)\ underset~i\ text(components at)\ \ t= pi/6 :`

`-1 + 4cos(pi/6)` `= 3 sec(pi/6)-1`
`-1 + 4 · sqrt3/2` `= 3· 2/sqrt3-1`
`2sqrt3` `= 2sqrt3`

 
`:.\ text(Particles collide.)`

 

b.ii.   `text(Collision occurs at)\ \ r(pi/6)`

`r(pi/6)` `= (-1 + 4cos\ pi/6, 2/sqrt3 sin\ pi/6)`
  `= (-1 + 2sqrt3, 1/sqrt3)`
♦ Mean mark part (c)(i) 37%.

 

c.i.   `d/dx (8sin^(-1) ((x + 1)/4) + ((x + 1)sqrt(-x^2 -2x + 15))/2)`

`= 8/(sqrt(1-((x + 1)/4)^2)) xx 1/4 + ((x + 1))/2 xx (-2x-2)/(2sqrt(-x^2-2x + 15)) + sqrt(-x^2-2x + 15) xx 1/2`

`= 8/(sqrt(16-(x + 1)^2))-((x + 1)^2)/(2sqrt(-x^2-2x + 15)) + sqrt(-x^2 -2x + 15)/2`

`= 16/(2sqrt(-x^2-2x + 15))-((x + 1)^2)/(2sqrt(-x^2-2x + 15))+ (-x^2-2x + 15)/(2sqrt(-x^2-2x + 15))`

`= (16-x^2-2x-1-x^2-2x + 15)/(2sqrt(-x^2-2x + 15))`

`= (2(-x^2-2x + 15))/(2sqrt(-x^2-2x + 15))`

`= sqrt(-x^2-2x + 15)`

♦ Mean mark part (c)(ii) 45%.

 

c.ii.    `text(Area)` `= int_1^(2sqrt3-1) sqrt3/6 sqrt(-x^2-2x + 15)\ dx`
    `= sqrt3/6 int_1^(2sqrt3-1) sqrt(-x^2-2x + 15)\ dx`
    `= sqrt3/6 [8sin^(-1)((x + 1)/4) + ((x + 1)sqrt(-x^2-2x + 15))/2]_1^(2sqrt3-1)`
    `= sqrt3/6 [(8sin^(-1)(sqrt3/2) + 2sqrt3 sqrt(-(2sqrt3 -1)^2-2(2sqrt3-1) + 15)/2)-(8sin^(-1)(1/2) + (2sqrt(-1-2 + 15))/2)]`
    `= sqrt3/6 [(8pi)/3 + sqrt3 sqrt(-12 + 4sqrt3-1-4sqrt3 + 2 + 15)-((8pi)/6 + sqrt12)]`
    `= sqrt3/6 ((8pi)/3 + 2sqrt3-(8pi)/6-2sqrt3)`
    `= sqrt3/6 ((8pi)/6)`
    `= (2sqrt3pi)/9`

Complex Numbers, SPEC1 2021 VCAA 8

  1. Solve  `z^2 + 2z + 2 = 0`  for `z`, where  `z ∈ C`.   (1 mark)

  2. Solve  `z^2 + 2barz + 2 = 0`  for `z`, where  `z ∈ C`.   (3 marks)

Show Answers Only
  1. `z = -1-i\ \ text(or)\ \ -1 + i`
  2. `z = 1 ± sqrt5 i`
Show Worked Solution
a.    `z^2 + 2z + 2` `= 0`
  `z^2 + 2z + 1 + 1` `= 0`
  `(z + 1)^2 + 1` `= 0`
  `(z + 1)^2-i^2` `= 0`
  `(z + 1 + i)(z + 1-i)` `= 0`

 
`:. z = -1-i\ \ \ text(or)\ \ -1 + i`

 

b.   `z = x + yi \ => \ barz = x-yi`

♦♦ Mean mark part (b) 28%.
`z^2 + 2barz + 2` `= 0`
`(x + yi)^2 + 2(x-yi) + 2` `= 0`
`x^2 + 2xyi-y^2 + 2x-2yi + 2` `= 0`
`x^2-y^2 + 2x + 2 + (2xy-2y)i` `= 0`

 

`text(Find)\ \ x, y\ text(such that)`

`x^2-y^2 + 2x + 2` `= 0\ …\ (1)`
`2xy-2y` `= 0\ …\ (2)`

 
`text(When)\ \ 2xy-2y = 0`

`2y(x-1)` `= 0`
`x` `= 1`

 
`text(Substitute)\ \ x = 1\ \ text{into (1)}`

`1-y^2 + 2 + 2` `= 0`
`y^2` `= 5`
`y` `= ±sqrt5`

 
`:. z = 1 ± sqrt5 i`

Calculus, EXT1 C3 2021 SPEC1 7

The velocity of a particle satisfies the differential equation  `(dx)/(dt) = xsin(t)`,  where  `x`  centimetres is its displacement relative to a fixed point `O` at time `t` seconds.

Initially, the displacement of the particle is 1 cm.

  1. Find an expression for `x` in terms of `t`.  (3 marks)

  2. Find the maximum displacement of the particle and the times at which this occurs.  (2 marks)

Show Answers Only
  1. `x = e^(1 – cos(t))`
  2. `x_text(max) = e^2\ \ text(when)\ \ t = pi, 3pi, 5pi, …`

     

    `text(or)\ t = (2k + 1)pi\ \ text(for integral)\ \ k =0,1,2,…`

Show Worked Solution
a.    `(dx)/(dt)` `= x sin(t)`
  `int 1/x\ dx` `= int sin(t)\ dt`
  `log_e x` `= -cos(t) + c`

 

`text(When)\ \ t = 0, x = 1`

`log_e 1` `= -cos0 + c`
`c` `= 1`
`log_e x` `= -cos(t) + 1`
`:. x` `= e^(1 – cos(t))`

 

b.    `x` `= e^(1 – cos(t))`
  `(dx)/(dt)` `= sin(t) · e^(1 – cos(t))`

`text(Find)\ \ t\ \ text(when)\ \ (dx)/(dt) = 0:`

`e^(1 – cos(t)) != 0`

`sin(t) = 0\ \ text(when)\ \ t = 0, pi, 2pi, …`

`x_text(max) = e^2\ \ text(when)\ \ t = pi, 3pi, 5pi, …`

`text(or)\ \ t = (2k + 1)pi\ \ text(for integral)\ \ k =0,1,2,…`

Calculus, SPEC1 2021 VCAA 7

The velocity of a particle satisfies the differential equation  `(dx)/(dt) = xsin(t)`,  where  `x`  centimetres is its displacement relative to a fixed point `O` at time `t` seconds.

Initially, the displacement of the particle is 1 cm.

  1. Find an expression for `x` in terms of `t`.   (3 marks)

  2. Find the maximum displacement of the particle and the times at which this occurs.   (2 marks)

Show Answers Only
  1. `x = e^(1-cos(t))`
  2. `x_text(max) = e^2\ \ text(when)\ \ t = pi, 3pi, 5pi, …`

     

    `text(or)\ t = (2k + 1)pi\ \ text(for)\ \ k ∈ Z^+ ∪ {0}`

Show Worked Solution
a.    `(dx)/(dt)` `= x sin(t)`
  `int 1/x\ dx` `= int sin(t)\ dt`
  `log_e x` `= -cos(t) + c`

 

`text(When)\ \ t = 0, x = 1`

`log_e 1` `= -cos0 + c`
`c` `= 1`
`log_e x` `= -cos(t) + 1`
`:. x` `= e^(1-cos(t))`

 

b.    `x` `= e^(1-cos(t))`
  `(dx)/(dt)` `= sin(t) · e^(1-cos(t))`

`text(Find)\ \ t\ \ text(when)\ \ (dx)/(dt) = 0:`

♦♦ Mean mark part (b) 25%.

`e^(1-cos(t)) != 0`

`sin(t) = 0\ \ text(when)\ \ t = 0, pi, 2pi, …`

`x_text(max) = e^2\ \ text(when)\ \ t = pi, 3pi, 5pi, …`

`text(or)\ \ t = (2k + 1)pi\ \ text(for)\ \ k ∈ Z^+ ∪ {0}`

Calculus, SPEC1 2021 VCAA 4

  1. The shaded region in the diagram below is bounded by the graph of  `y = sin(x)`  and the `x`-axis between the first two non-negative `x`-intercepts of the curve, that is interval  `[0, pi]`.  The shaded region is rotated about the `x`-axis to form a solid of revolution.
     
           
     
    Find the volume, `V_s` of the solid formed.   (3 marks)

  2. Now consider the function  `y = sin(kx)`, where `k` is a positive real constant. The region bounded by the graph of the function and the `x`-axis between the first two non-negative `x`-intercepts of the graph is rotated about the `x`-axis to form a solid of revolution.
  3. Find the volume of this solid in term of `V_s`.   (1 mark)

Show Answers Only

  1. `(pi^2)/2\ text(u)³`
  2. `1/k V_s`

Show Worked Solution

a.    `V_s` `= pi int_0^pi sin^2(x)\ dx`
    `= pi int_0^pi 1/2(1-cos(2x))\ dx`
    `= pi/2 int_0^pi 1-cos(2x)\ dx`
    `= pi/2 [x-1/2 sin(2x)]_0^pi`
    `= pi/2[pi-1/2 sin(2pi)-(0-1/2 sin 0)]`
    `= (pi^2)/2\ text(u)³`

♦♦ Mean mark part (b) 30%.

 

b.   `y = sin(kx)\ \ text(is the dilation of)\ \ y = sin(x)\ \ text(by a factor of)`

`k\ \ text(from the)\ \ xtext(-axis)`

`:. V = 1/k V_s`

Statistics, SPEC1 2021 VCAA 3

A company produces a particular type of light globe called Shiny. The company claims that the lifetime of these globes is normally distributed with a mean of 200 weeks and it is known that the standard deviation of the lifetime of Shiny globes is 10 weeks. Customers have complained, saying Shiny globes were lasting less than the claimed 200 weeks. It was decided to investigate the complaints. A random sample of 36 Shiny globes was tested and it was found that the mean lifetime of the sample was 195 weeks.

Use  `text(Pr)(-1.96 < Z < 1.96) = 0.95`  and  `text(Pr)(-3 < Z < 3) = 0.9973`  to answer the following questions.

  1. Write down the null and alternative hypotheses for the one-tailed test that was conducted to investigate the complaints.   (1 mark)

    1. Determine the `p` value, correct to three places decimal places, for the test.   (2 marks)

    2. What should the company be told if the test was carried out at the 1% level of significance?   (1 mark)

  3. The company decided to produce a new type of light globe called Globeplus.
    Find the approximate 95% confidence interval for the mean lifetime of the new globes if a random sample of 25 Globeplus globes is tested and the sample mean is found to be 250 weeks. Assume that the standard deviation of the population is 10 weeks. Give your answer correct to two decimal places.   (1 mark)

Show Answers Only
  1. `H_0 : mu = 200`
    `H_1 : mu < 200`
    1. `0.001\ \ (text(to 3 d.p.))`
    2. `(246.08, 253.92)`
  3. `text(Reject the null hypothesis.)`
Show Worked Solution

a.   `H_0 : mu = 200`

`H_1 : mu < 200`

 

b.i.   `E(barX) = mu = 200`

♦ Mean mark part (b)(i) 48%.

`sigma(barX) = sigma/sqrtn = 10/sqrt36 = 5/3`

`p` `= text(Pr)(barX< 195 | mu = 200)`
  `= text(Pr)(z < (195-200)/(3/5))`
  `= text(Pr)(z < -3)`
  `= 1/2 (1-0.9973)`
  `= 0.00135`
  `= 0.001\ \ (text(to 3 d.p.))`

 

b.ii.   `text(1% level) => 0.01`

♦ Mean mark part (b)(ii) 49%.

  `text(S)text(ince)\ \ 0.001 < 0.01\ \ =>\ text(Strong evidence against)\ H_0`

  `:.\ text(Reject the null hypothesis.)`

 

c.   `sigma(barx) = sigma/sqrtn = 10/sqrt25 = 2`

`text(95% C.I.)` `= barx-1.96 xx 2, barx + 1.96 xx 2`
  `= (250-3.92, 250 + 3.92)`
  `= (246.08, 253.92)`

GRAPHS, FUR1 2021 VCAA 7 MC

The feasible region for a linear programming problem is shaded in the diagram below.
 

Which objective function, `Z`, will not have a maximum value at the point `K`?

  1. `Z = x + y`
  2. `Z = x + 3y`
  3. `Z = 2x + 3y`
  4. `Z = 3x + 2y`
  5. `Z = 5x + 3y`
Show Answers Only

`B`

Show Worked Solution

`K \ text{occurs at intersection of}`

♦ Mean mark 39%.

`y = – 1/2 x + 40 \ \ text{and}\ \ y = -2x + 100`

`text{Maximum at} \ K \ text{if} \  -2 ≤ m ≤ -1/2`
 
`text{Consider each option:}`

`A: \ Z = x + y \ -> \ y = Z – x \ -> \ m = -1 qquad✓`

`B: \ Z = x + 3y \ -> \ y = {Z – x}/{3} \ -> \ m = – 1/3 \ qquad ✘`

`C: \ Z = 2x + 3y \ -> \ y = {Z – 2x}/{3} \ -> \ m = -2/3 qquad ✓`

`D: \ Z = 3x + 2y \ -> \ y = {Z – 3x}/{2} -> m = -3/2 qquad ✓`

`E: \ Z = 5x + 3y \ -> \ y = {Z – 5x}/{3} \ -> \ m = – 5/3 qquad ✓`
 

`=> B`

GRAPHS, FUR1 2021 VCAA 6 MC

The graph below shows a relationship between `1/x` and `y`.

The rule that represents this relationship between `x` and `y` is

  1. `y = 1/{10x}`
  2. `y = 5/(2x)`
  3. `y = 10/x`
  4. `y = 2/(5x)`
  5. `y = x/10`
Show Answers Only

`D`

Show Worked Solution

♦ Mean mark 42%.
`y` `= k xx 1/x qquadqquad text{(linear relationship)}`
`2` `= 5k qquadqquad ( text{note} \ 1/x = 5 , \ text{not} \ x = 5)`
`k` `= 2/5`

 
`:. y = 2/(5x)`
 

`=> D`

GRAPHS, FUR1 2021 VCAA 4 MC

A railway station in the city has two car parks, Eastpark and Northpark.

At Eastpark, cars can be parked for up to 10 hours per day

The fees for Eastpark are as follows.

`text{fee} = {{:($6 text{,}),($10 text{,}),($14 text{,}):}\ \ \ \ {:(0 < text{hours} ≤ 3),(3 < text{hours} ≤ 6),(6 < text{hours} ≤ 10):}:}`
 

Northpark charges fees according to the formula

`text{fee} = $2.30 xx text{hours}`

Lani wants to park her car for seven hours on Wednesday and four hours on Thursday.

She may choose either car park on each day.

The minimum total fee that Lani will pay for parking for the two days is

  1. $16.00
  2. $20.00
  3. $23.20
  4. $24.00
  5. $25.30
Show Answers Only

`C`

Show Worked Solution

`text{Wednesday cost}`

♦ Mean mark 44%.

`text{East $14,  North} = 2.30 xx 7 = $ 16.10`

`text{Thursday cost}`

`text{East $10,  North} = 2.30 xx 4 = $9.20`

`:.\ text{Minimum fee}` `= 14 + 9.20`
  `= $23.20`

  
`=> C`

GEOMETRY, FUR1 2021 VCAA 8 MC

Rod and Lucia went on a bushwalk.

They walked 1400 m from the car park to reach a lookout that was directly east of the car park.

From the lookout, Rod returned to the car park via a café and Lucia returned to the car park via a swimming hole.

    • The bearing of the swimming hole from the lookout is 290°.
    • The bearing of the cafe from the lookout is 240°.
    • The swimming hole is 950 m from the car park.
    • The cafe is 700 m from the car park.
    • The swimming hole is coser to the lookout than it is to the car park.

In relation to the total distance each of them individually walked from the lookout back to the car park, which one of the following statements is true?

  1. Rod and Lucia walked the same distance.
  2. Rod walked 467 m further than Lucia, to the nearest metre.
  3. Rod walked 717 m further than Lucia, to the nearest metre.
  4. Lucia walked 924 m further than Rod, to the nearest metre.
  5. Lucia walked 1174 m further than Rod, to the nearest metre.
Show Answers Only

`B`

Show Worked Solution

`text{Using cosine rule in} \ Δ PSL`

♦♦ Mean mark 30%.

`text{Solve  for}\ d_1\ text{using CAS:}`

`950^2` `= 1400^2 + d_1^2 – 2 xx 1400 xx d_1 xx cos 20`
`d_1` `= 495.06 \ text{or} \ 2136.07`
`d_1` `=495.06 \ text{(closer to L than P)}`

   
`text{Using cosine rule in} \ Δ PCL`

`text{Solve for} \ d_2 \ text{using CAS:}`

`700^2` `= 1400^2 + d_2^2 – 2 xx 1400 xx d_2 xx cos30`
`d_2` `=1212.43`

 

`text{Distance (Rod)}` `= 700 + 1212.4`
  `= 1912.4`

 

`text{Distance (Lucia)}` `= 495.1 + 950`
  `= 1445.1`

 

`:. \ text{Extra distance}` `= 1912.4 – 1445.1`
  `= 467.3 \ text{m}`

`=> B`

GEOMETRY, FUR1 2021 VCAA 7 MC

A composite shape is made up of two triangles, as shown in the diagram below.

Two angles, `a^@`  and  `b^@`, are shown on the diagram.
 

Which one of the following statements is always true?

  1. `2a^@ = b^@`
  2. `a^@ = 180^@ - b^@`
  3. `a^@ = 180^@ - 2b^@`
  4. `a^@ = 2b^@ - 180^@`
  5. `2a^@ = 180^@ - b^@`
Show Answers Only

`D`

Show Worked Solution

`text{Base angles of isosceles} \ Δ`

♦♦ Mean mark 32%.

`qquad = 1/2 (180 – a)`
 

`:. 1/2 (180 – a) + b` `= 180`
`180 – a + 2b` `= 360`
`2b – a` `= 180`
`:. a` `= 2b – 180`

 
`=> D`

GEOMETRY, FUR1 2021 VCAA 6 MC

A child's toy has the following design.
 

The area of the shaded region, in square centimetres, is closest to

  1.   13
  2.   27
  3.   31
  4.   45
  5. 113
Show Answers Only

`B`

Show Worked Solution

`text{Circle radius = 3 cm}`

♦ Mean mark 45%.

`text(Consider the rectangle starting from the middle of the left circle.)`

`text{Shaded Area}` `= text{Area rectangle} –  3.5 xx text{Area circle}`
  `= (21 xx 6) – 3.5 xx pi xx 3^2`
  `= 27.03 …\ text{cm}^2`

`=> B`

GEOMETRY, FUR1 2021 VCAA 5 MC

A cone and a cylinder both have a radius of `r` centimetres.

The height of the cone is 12 cm.

If the cylinder and the cone have the same volume, then the height of the cylinder, in centimetres, is

  1.   4
  2.   6
  3.   8
  4. 12
  5. 36
Show Answers Only

`A`

Show Worked Solution

♦ Mean mark 46%.
`V_text{cone}` `= 1/3 pi r^2 h_1`
  `=1/3 xx pi xx r^2 xx 12`
  `= 4 pi r^2`

 

`V_text{cylinder}` `= pi r^2 h_2`
`4 pi r^2` `= pi r^2 h_2`
`:. \ h_2` `=4`

 
`=> A`

GEOMETRY, FUR1 2021 VCAA 3 MC

A photograph was enlarged by an area scale factor of 9.

The length of the original photograph was 12 cm.

The original photograph and the enlarged photograph are similar in shape.

The length of the enlarged photograph, in centimetres, is

  1.    4
  2.    9
  3.  27
  4.  36
  5. 108
Show Answers Only

`D`

Show Worked Solution

`text{Area scale factor} = 9`

♦ Mean mark 38%.

`text{Length sale factor} = sqrt9 = 3`

`:. \ text{Length of large photo}` `= 12 xx 3`
  `= 36 \ text{cm}`

`=> D`

Networks, STD2 N3 2021 FUR1 6

The directed graph below shows the sequence of activities required to complete a project.

The time taken to complete each activity, in hours, is also shown.
 

The minimum completion time for this project is 18 hours.

The time taken to complete activity `E` is labelled  `x`.

What is the maximum value of  `x`?   (2 marks)

Show Answers Only

`text(3 hours)`

Show Worked Solution

`text{Consider all possible network paths:}`

`ADHJ \ -> \ text{18 hours}`

`BEJ \ -> \ (12 + x) \ text{hours}`

`CGFEJ \ -> \  (15 + x) \ text{hours}`

`CGIJ \ -> \ text{18 hours}`
 

`text{Minimum completion time = 18 hours}`

`=>\ text{No path can be longer than 18 hours}`

`:. \ x_text{max} = 3 \ text{hours}`

Networks, STD2 N2 2021 FUR1 8 MC

A network of roads connecting towns in an alpine region is shown below.

The distances between neighbouring towns, represented by vertices, are given in kilometres.
 

The region receives a large snowfall, leaving all roads between the towns closed to traffic.

To ensure each town is accessible by car from every other town, some roads will be cleared.

The minimal total length of road, in kilometres, that needs to be cleared is

  1. 361 if  `x` = 50 and  `y` = 55
  2. 361 if  `x` = 50 and  `y` = 60
  3. 366 if  `x` = 55 and  `y` = 55
  4. 371 if  `x` = 55 and  `y` = 65
Show Answers Only

`B`

Show Worked Solution

`text{A partial minimal spanning tree can be drawn:}`
 

`text{Consider each option:}`

`A:\ text{If} \ x=50 \ text{(include),} \ y = 55 \ text{(include)}`

   `-> \ text{Total length} = 251 + 50 + 55 != 361 \ text{(incorrect)}`

`B:\ text{If} \ x=50 \ text{(include),} \ y = 60 \ text{(include)}`

   `-> \ text{Total length} = 251 + 50 + 55 = 356 \ text{(correct)}`

`text{Similarly, options} \ C, D, E \ text{can be shown to be incorrect.}`

`=> B`

NETWORKS, FUR1 2021 VCAA 7 MC

The network below shoes the pathways between five buildings: `J`, `K`, `L`, `M`, and `N`. 
 

An adjacency matrix for this network is formed.

The number of zeros in this matrix is

  1.   8
  2.   9
  3. 10
  4. 11
  5. 12
Show Answers Only

`C`

Show Worked Solution

`text{Adjacency matrix:}`

♦♦ Mean mark 33%.

 

`{:(qquadqquad J\ \ \ Kquad L\ \ M \ \ N),({:(J),(K),(L),(M),(N):}[(0,2,1,0,1),(2,1,2,1,0),(1,2,0,1,1),(0,1,1,0,0),(1,0,1,0,0)]):}`
 

`=> C`

NETWORKS, FUR1 2021 VCAA 6 MC

The directed graph below shows the sequence of activities required to complete a project.

The time taken to complete each activity, in hours, is also shown.
 

The minimum completion time for this project is 18 hours.

The time taken to complete activity `E` is labelled  `x`.

The maximum value of  `x`  is

  1. 2
  2. 3
  3. 4
  4. 5
  5. 6
Show Answers Only

`B`

Show Worked Solution

`text{Consider all possible network paths:}`

♦ Mean mark 46%.

`ADHJ \ -> \ text{18 hours}`

`BEJ \ -> \ (12 + x) \ text{hours}`

`CGFEJ \ -> \  (15 + x) \ text{hours}`

`CGIJ \ -> \ text{18 hours}`
 

`text{Minimum completion time = 18 hours}`

`:. \ text{No path can be longer than 18 hours}`

`:. \ x_text{max} = 3 \ text{hours}`
 

`=> B`

MATRICES, FUR1 2021 VCAA 7 MC

The matrix  `S_{n + 1}`  is determined from the matrix  `S_n`  using the recurrence relation  `S_{n + 1} = T xx S_n - C`, where

`T= [(0.6,0.1,0.3),(0.3,0.8,0.2),(0.1,0.1,0.5)] , qquad S_0 = [(21),(51),(31)], qquad S_1 = [(24.0),(54.3),(20.7)] `

and  `C` is a column matrix. 

Matrix  `S_2`  is equal to

A.  `[(23.04),(55.78),(16.18)]` B.  `[(25.34),(56.28),(17.38)]`  
     
C.  `[(26.04),(54.78),(18.18)]` D.  `[(28.34),(55.28),(19.38)]`  
     
E.  `[(29.04),(53.78),(20.18)]`    
Show Answers Only

`A`

Show Worked Solution

`S_1 = TS_0 – C`

♦ Mean mark 40%.
`[(24.0),(54.3),(20.7)]` `= [(0.6,0.1,0.3),(0.3,0.8,0.2),(0.1,0.1,0.5)] [(21),(51),(31)] – C`
`[(24.0),(54.3),(20.7)]` `= [(27),(53.3),(22.7)] – C`
`C` `= [(27),(53.3),(22.7)] – [(24.0),(54.3),(20.7)] = [(3),(-1),(2)]`

 
`S_2 = TS_1 – C`

`S_2` `= [(0.6,0.1,0.3),(0.3,0.8,0.2),(0.1,0.1,0.5)] [(24.0),(54.3),(20.7)] – [(3),(-1),(2)]`
  `= [(23.04),(55.78),(16.18)]`

`=> A`

MATRICES, FUR1 2021 VCAA 5 MC

`A`  is a 7 × 7 matrix.

`B`  is a 10 × 7 matrix.

Which one of the following matrix expressions is defined?

  1. `AB - 2B`
  2. `A(BA)^-1`
  3. `AB^2`
  4. `A^2 - BA`
  5. `A(B^T)`
Show Answers Only

`E`

Show Worked Solution

`text{Consider each option}`

♦ Mean mark 45%.

`A : \ AB-2B -> text{not defined (AB not defined)}`

`B : \ A(BA)^-1`

`BA -> (10 xx 7) (7 xx 7) -> (10 xx 7)`

`( BA)^-1 \ text{is not defined (inverse matrices only apply to square matrices)}`

`C : \ AB^2 -> text{not defined} \ (B^2 \ text{not defined – only square matrices can be raised to a power)}`

`D : \ A^2 – BA`

`A^2 -> (7 xx 7), \ BA -> (10 xx 7)`

`qquad  \ A^2 – BA \ -> text{not defined (only matrices of the same order can be subtracted)}`

`E: \ A(B^T)`

`A -> (7 xx 7), \ B^T -> (7 xx 10)`

`A (B^T) \ text{is defined as Columns in} \ A = \ text{rows in} \ B^T`
 

`=> E`

Calculus, MET1 2021 VCAA 8

The gradient of a function is given by  `(dy)/(dx) = sqrt(x + 6)-x/2-3/2`.

The graph of the function has a single stationary point at  `(3, 29/4)`.

  1. Find the rule of the function.   (3 marks)

  2. Determine the nature of the stationary point.   (2 marks)

Show Answers Only
  1. `y=2/3(x+6)^(3/2)-x^2/4-3/2x-4`
  2. `text{Maximum}`
Show Worked Solution
a.    `dy/dx` `= sqrt(x + 6)-x/2-3/2`
  `y` `=int sqrt(x + 6)-x/2-3/2\ dx`
    `=2/3(x+6)^(3/2)-x^2/4-3/2x + c`

 
`text{Graph passes through}\ (3, 29/4)`

`29/4` `=2/3*9^(3/2)-3^2/4-3/2 * 3+c`  
`29/4` `=18-9/4-9/2+c`  
`c` `=29/4-18+9/4+9/2`  
  `=-4`  

 
`:. y=2/3(x+6)^(3/2)-x^2/4-3/2x-4`

♦ Mean mark part (b) 37%.

b. 
      

`:.(3,29/4)\ text{is a maximum}.`

Probability, MET1 2021 VCAA 7

A random variable  `X`  has the probability density function  `f`  given by

`f(x) = {{:(k/(x^2)),(0):}\ \ \ \ {:(1 <= x <= 2),(text{elsewhere}):}:}`

where  `k`  is a positive real number.

  1. Show that  `k = 2`.  (1 mark)

  2. Find  `E(X)`.  (2 marks)

Show Answers Only

  1. `text(See Worked Solution)`
  2. `2log_e2`

Show Worked Solution

♦ Mean mark part (a) 48%.

a.    `int_1^2 k/x^2\ dx` `=1`
  `k[- 1/x]_1^2` `=1`
  `k(-1/2+1)` `=1`
  `k/2` `=1`
  `:.k` `=2\ \ text{… as required}`

 

♦ Mean mark part (b) 44%.
MARKER’S COMMENT: Common error not recognising  `log_e1=0`

b.    `E(X)` `=int_1^2 x * 2/x^2\ dx`
    `=int_1^2 2/x\ dx`
    `=[2log_e x]_1^2`
    `=2log_e2-2log_e1`
    `=2log_e2`

Graphs, MET1 2021 VCAA 4

  1. Sketch the graph of  `y = 1-2/(x-2)`  on the axes below. Label asymptotes with their equations and axis intercepts with their coordinates.   (3 marks)

     

     

  2. Find the values of  `x`  for which  `1-2/(x-2) >= 3`.   (1 mark)

Show Answers Only

a. 

b. `x in [1, 2)`

Show Worked Solution

a.   `text(Asymptotes:)`

`x=2`

`text(As)\ \ x→ +-oo, \ y→1\ \ =>\ text(Asymptote at)\ \ y=1`

`ytext(-intercept at)\ (0,2)`

`xtext(-intercept at)\ (4,0)`

♦ Mean mark part (b) 32%.

b.   `text(By inspection of the graph:)`

`1-2/(x-2) >=3\ \ text(for)\ \ x in [1, 2)`

Probability, MET1 2021 VCAA 6

An online shopping site sells boxes of doughnuts.

A box contains 20 doughnuts. There are only four types of doughnuts in the box. They are:

    • glazed, with custard
    • glazed, with no custard
    • not glazed, with custard
    • not glazed, with no custard

It is known that, in the box:

    • `1/2`  of the doughnuts are with custard
    • `7/10`  of the doughnuts are not glazed
    • `1/10`  of the doughnuts are glazed, with custard
  1. A doughnut is chosen at random from the box.
  2. Find the probability that it is not glazed, with custard.  (1 mark)

  3. The 20 doughnuts in the box are randomly allocated to two new boxes, Box A and Box B.
  4. Each new box contains 10 doughnuts.
  5. One of the two new boxes is chosen at random and then a doughnut from that box is chosen at random.
  6. Let `g` be the number of glazed doughnuts in Box A.
  7. Find the probability, in terms of `g`, that the doughnut comes from box B given that it is glazed.  (2 marks)

  8. The online shopping site has over one million visitors per day.
  9. It is know that half of these visitors are less than 25 years old.
  10. Let  `overset^P`  be the random variable representing the proportion of visitors who are less than 25 years old in a random sample of five visitors.
  11. Find  `text{Pr}(overset^P >= 0.8)`. Do not use a normal approximation.  (3 marks)

Show Answers Only

  1. `2/5`
  2. `(6-g)/6`
  3. `3/16`

Show Worked Solution

a.   `text(Create a 2-way table:)`

`text{Pr(not glazed with custard)}` `=8/20`  
  `=2/5`  

 
b.   `A_text{glazed} = g \ => \ B_text{glazed} = 6-g`

♦♦♦ Mean mark part (b) 20%.

`text{Pr(glazed)} = 6/20`

`text{Pr}(B | text{glazed})` `= (text{Pr}(B ∩ text{glazed}))/text{Pr(glazed)}`  
  `=(1/2 xx (6-g)/10)/(6/20)`  
  `=(6-g)/20 xx 20/6`  
  `=(6-g)/6`  

 
c.   `text(Let)\ \ X=\ text(number of visitors < 25 years)`

♦ Mean mark part (c) 40%.

`X\ ~\ text{Bi}(5, 0.5)`

`text{Pr}(hatP>=0.8)` `= text{Pr}(X>=4)`  
  `=\ ^5C_4 * (1/2)^4(1/2) + (1/2)^5`  
  `=5/32 + 1/32`  
  `=3/16`  

CORE, FUR1 2021 VCAA 24 MC

Bob borrowed $400 000 to buy an apartment.

The interest rate for this loan was 3.14% per annum, compounding monthly.

A scheduled monthly repayment that allowed Bob to fully repay the loan in 20 years was determined.

Bob decided, however, to make interest-only repayments for the first two years.

After these two years the interest rate changed. Bob was still able to pay off the loan in the 20 years by repaying the scheduled amount each month.

The interest rate, per annum, for the final 18 years of the loan was closest to

  1. 1.85%
  2. 2.21%
  3. 2.79%
  4. 3.14%
  5. 4.07%
Show Answers Only

`B`

Show Worked Solution

`text{Find original payment (by TVM Solver):}`

♦♦ Mean mark 33%.
`N` `= 24 xx 12 = 240`
`Itext{(%)}` `= 3.14`
`PV` `= 400\ 000`
`PMT` `= ?`
`FV` `= 0`
`text(P/Y)` `= text(C/Y) = 12`

 
`:. PMT = 2246.528`
 

`text{Find new} \ I text{(%)} \ text{(by TVM Solver):}`

`N` `= 18 xx 12 = 216`
`Itext{(%)}` `= ?`
`PV` `= 400\ 000`
`PMT` `= -2246.53`
`FV` `= 0`
`text(P/Y)` `= text(C/Y) = 12`

  
`:.  I text{(%)} = 2.21`

`=> B`

CORE, FUR1 2021 VCAA 23 MC

Bimal has a reducing balance loan.

The balance, in dollars, of the loan from month,  `B_n`, is modelled by the recurrence relation below.

`B_o = 450\ 000, \ B_{n+1} = RB_n - 2633`

Given that the loan will be fully repaid in 20 years, the value of `R` is closest to

  1. 1.003
  2. 1.0036
  3. 1.03
  4. 1.036
  5. 1.36
Show Answers Only

`A`

Show Worked Solution

`text{By TVM Solver:}`

♦♦ Mean mark 31%.
`N` `= 240`
`Itext{(%)}` `= ?`
`PV` `= 450\ 000`
`PMT` `= -2633`
`FV` `= 0`
`text(P/Y)` `= text(C/Y) = 12`

 
`:. Itext{(%)}= 3.5999 …`
 

`r_text{monthly} = 3.6/12 = 0.3`

`R` `= 1 + r/100`
  `= 1 + 0.3/100`
  `=1.003`

 
`=> A`

CORE, FUR1 2021 VCAA 21 MC

Enrico invests $3000 in an account that pays interest compounding monthly.

After four years, the balance of the account is $3728.92

The effective annual interest rate for this investment, rounded to two decimal places, is

  1. 5.45%
  2. 5.52%
  3. 5.56%
  4. 5.59%
  5. 5.60%
Show Answers Only

`D`

Show Worked Solution

`text{By TVM Solver:}`

♦ Mean mark 40%.
`N` `= 48`
`I(%)` `= ?`
`PV` `= -3000`
`PMT` `= 0`
`FV` `= 3728.92`
`text(P/Y)` `= text(C/Y) = 12`

 
`=> I(%) = 5.45text(%)`

`r_text{effective}` `= [(1 + {5.45}/{100 xx 12})^12 -1] xx 100text(%)`
  `= 5.588 …%`

`=> D`

CORE, FUR1 2021 VCAA 20 MC

Sammy purchased a boat for $72 000.

The value of the boat is depreciated each year by 10% using the reducing balance method.

In the third year, the boat will depreciate in value by 10% of

  1. $47 239.20
  2. $52 488.00
  3. $58 320.00
  4. $64 800.00
  5. $72 000.00
Show Answers Only

`C`

Show Worked Solution

♦ Mean mark 44%.
`V_1` `= 72 000 xx 0.9`
  `= 64\ 800`
`V_2` `= 64\ 800 xx 0.9`
  `= 58\ 320`

 
`:. \ text{Depreciation in 3rd year will be 10% of $58 320}`
 

`=> C`

CORE, FUR1 2021 VCAA 14 MC

A garden centre sells garden soil.

The table below shows the daily quantity of garden soil sold, in cubic metres, over a one-week period.
 

The quantity of garden soil sold on Wednesday, Thursday and Friday is not shown.

The five-mean smoothed quantity of garden soil sold on Thursday is 206 m3.

The three-mean smoothed quantity of garden soil sold on Thursday, in cubic metres, is

  1. 143
  2. 166
  3. 206
  4. 239
  5. 403
Show Answers Only

`B`

Show Worked Solution

`text{Let} \ x = \ text{amount sold Wednesday – Friday}`

♦ Mean mark 48%.
`{x + 186 + 346}/5` `= 206`
`x` `= (206 xx 5) – 186 – 346`
  `= 498 \ text{m}^3`

 
`:. \ text{Three-mean smoothed quantity (Thursday)}`

`=498/3`

`=166\ text(m³)`
 

`=> B`

CORE, FUR1 2021 VCAA 12 MC

The time series plot below shows the quarterly sales, in thousands of dollars, of a small business for the years 2010 to 2020.
 

The time series plot is best described as having

  1. seasonality only.
  2. irregular fluctuations only.
  3. seasonality with irregular fluctuations. 
  4. a decreasing trend with irregular fluctuations.
  5. a decreasing trend with seasonality and irregular fluctuations.
Show Answers Only

`D`

Show Worked Solution

`text{The peaks and troughs both show a decreasing trend.}`

♦♦ Mean mark 34%.

`text{Fluctuations within any year are irregular and don’t}`

`text{display any seasonality.}`

`=> D`

CORE, FUR1 2021 VCAA 11 MC

The table below shows the weight, in kilograms, and the height, in centimetres, of 10 adults.

A least squares line is fitted to the data

The least squares line enables an adult's weight to be predicted from their height.

The number of times that the predicted value of an adult's weight is greater than the actual value of their weight is

  1. 3
  2. 4
  3. 5
  4. 6
  5. 7
Show Answers Only

`D`

Show Worked Solution

`text(S)text(ince weight is being predicted from height,)`

♦ Mean mark 40%.

`text{Weight} -> text{response} \ (y text{-value})`

`text{Height} -> text{explanatory} \ (x text{-value})`

`text{Using CAS, the graph and scatterplot show that 6 points lie below the regression line}`

`text{(where predicted weight > actual)}`

`=> D`

CORE, FUR1 2021 VCAA 1-3 MC

The percentaged segmented bar chart below shows the age (under 55 years, 55 years and over) of visitors at a travel convention, segmented by preferred travel destination (domestic, international).
 

Part 1

The variables age (under 55 years, 55 years and over) and preferred travel destination (domestic, international) are

  1. both categorial variables.
  2. both numerical variables.
  3. a numerical variable and a categorical variable respectively.
  4. a categorical variable and a numerical variable respectively.
  5. a discrete variable and a continuous variable respectively.

 
Part 2

The data displayed in the percentaged segmented bar chart supports the contention that there is an association between preferred travel destination and age because

  1. more visitors favour international travel.
  2. 35% of visitors under 55 years favour international travel.
  3. 45% of visitors 55 years and over favour domestic travel.
  4. 65% of visitors under 55 years favour domestic travel while 45% of visitors 55 years and over favour domestic travel.
  5. the percentage of visitors who prefer domestic travel is greater than the percentage of visitors who prefer international travel.

 
Part 3

The results could also be summarised in a two-way frequency table.

Which one of the following frequency tables could match the pecentaged segmented bar chart?

 

Show Answers Only

`text(Part 1:)\ A`

`text(Part 2:)\ D `

`text(Part 3:)\ A`

Show Worked Solution

`text(Part 1)`

`text{Preferred travel destination → categorical (nominal) variable}`

`text{Age → categorical (ordinal) variable}`

`=> A`
 

`text(Part 2)`

`text(Only option)\ D\ text(highlights a change in preference for domestic travel)`

`text(between the two age categories.)`

`=>D` 

 
`text(Part 3)`

♦ Mean mark 50%.

`text(Converting the frequency table data into percentages,)`

`text(consider option)\ A:`

`91/140 xx 100 = 65text(%),\ \ 49/140 xx 100 = 35text(%)`

`90/200 xx 100 = 45text(%), \ \ 110/200 xx 100 = 55text(%)`

`=> A`

Algebra, MET1 2021 VCAA 5

Let  `f:R -> R, \ f(x) = x^2 - 4`  and  `g:R -> R, \ g(x) = 4(x - 1)^2 - 4`.

  1. The graphs of `f` and `g` have a common horizontal axis intercept at `(2, 0)`.
  2. Find the coordinates of the other horizontal axis intercept of the graph of `g`.   (2 marks)

  3. Let the graph of `h` be a transformation of the graph of `f` where the transformations have been applied in the following order:
    • dilation by a factor of  `1/2`  from the vertical axis (parallel to the horizontal axis)
    • translation by two units to the right (in the direction of the positive horizontal axis
  4. State the rule of `h` and the coordinates of the horizontal axis intercepts of the graph of `h`.   (2 marks)

Show Answers Only
  1. `(0,0)`
  2. `(1,0) and (3,0)`
Show Worked Solution

a.   `xtext(-axis intercept of)\ g(x):`

`4(x-1)^2-4` `=0`  
`(x-1)^2` `=1`  
`x-1` `=+-1`  

 
`text(When)\ \ x-1=-1\ \ =>\ \ x=0`

`:.\ text{Other horizontal intercept occurs at (0, 0)}`
 

b.   `text(1st transformation)`

♦♦ Mean mark part (b) 25%.

`text(Dilation by a factor of)\ 1/2\ text(from the)\ ytext(-axis:)`

`x^2 – 4 \ → \ (x/(1/2))^2 -4 = 4x^2-4`
 

`text(2nd transformation)`

`text(Translation by 2 units to the right:)`

`4x^2-4 \ → \ h(x) = 4(x-2)^2 – 4`
 

`xtext(-axis intercept of)\ h(x):`

`4(x-2)^2-4` `=0`  
`(x-2)^2` `=1`  
`x-2` `=+-1`  

 
`x-2=1 \ => \ x=3`

`x-2=-1 \ => \ x=1`

`:.\ text(Horizontal axis intercepts occur at)\ (1,0) and (3,0).`